R - rozkład dwumianowy

Model rozkładu dwumianowego zajmuje się znajdowaniem prawdopodobieństwa sukcesu zdarzenia, które ma tylko dwa możliwe wyniki w serii eksperymentów. Na przykład rzucenie monetą zawsze daje głowę lub ogon. Prawdopodobieństwo znalezienia dokładnie 3 orłów podczas wielokrotnego rzucania monetą 10 razy szacuje się podczas rozkładu dwumianowego.

R ma cztery wbudowane funkcje do generowania rozkładu dwumianowego. Zostały opisane poniżej.

dbinom(x, size, prob)
pbinom(x, size, prob)
qbinom(p, size, prob)
rbinom(n, size, prob)

Poniżej znajduje się opis użytych parametrów -

x jest wektorem liczb.
p jest wektorem prawdopodobieństw.
n to liczba obserwacji.
size to liczba prób.
prob to prawdopodobieństwo sukcesu każdej próby.

dbinom ()

Ta funkcja daje rozkład gęstości prawdopodobieństwa w każdym punkcie.

# Create a sample of 50 numbers which are incremented by 1.
x <- seq(0,50,by = 1)

# Create the binomial distribution.
y <- dbinom(x,50,0.5)

# Give the chart file a name.
png(file = "dbinom.png")

# Plot the graph for this sample.
plot(x,y)

# Save the file.
dev.off()

Kiedy wykonujemy powyższy kod, daje on następujący wynik -

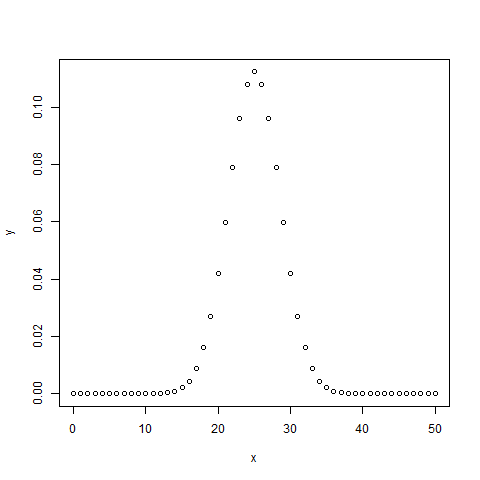
pbinom ()

Ta funkcja podaje skumulowane prawdopodobieństwo wystąpienia zdarzenia. Jest to pojedyncza wartość reprezentująca prawdopodobieństwo.

# Probability of getting 26 or less heads from a 51 tosses of a coin.
x <- pbinom(26,51,0.5)

print(x)

Kiedy wykonujemy powyższy kod, daje on następujący wynik -

[1] 0.610116

qbinom ()

Ta funkcja przyjmuje wartość prawdopodobieństwa i podaje liczbę, której skumulowana wartość odpowiada wartości prawdopodobieństwa.

# How many heads will have a probability of 0.25 will come out when a coin
# is tossed 51 times.
x <- qbinom(0.25,51,1/2)

print(x)

Kiedy wykonujemy powyższy kod, daje on następujący wynik -

[1] 23

rbinom ()

Funkcja ta generuje wymaganą liczbę losowych wartości o zadanym prawdopodobieństwie z danej próbki.

# Find 8 random values from a sample of 150 with probability of 0.4.
x <- rbinom(8,150,.4)

print(x)

Kiedy wykonujemy powyższy kod, daje on następujący wynik -

[1] 58 61 59 66 55 60 61 67