R - regresja liniowa

Analiza regresji jest bardzo szeroko stosowanym narzędziem statystycznym do ustalenia modelu relacji między dwiema zmiennymi. Jedna z tych zmiennych nazywana jest zmienną predykcyjną, której wartość jest gromadzona w drodze eksperymentów. Druga zmienna nazywana jest zmienną odpowiedzi, której wartość pochodzi ze zmiennej predykcyjnej.

W regresji liniowej te dwie zmienne są powiązane równaniem, w którym wykładnik (potęga) obu tych zmiennych wynosi 1. Z matematycznego punktu widzenia zależność liniowa przedstawia linię prostą w postaci wykresu. Nieliniowa zależność, w której wykładnik dowolnej zmiennej nie jest równy 1, tworzy krzywą.

Ogólne równanie matematyczne dla regresji liniowej to -

y = ax + b

Poniżej znajduje się opis użytych parametrów -

y jest zmienną odpowiedzi.
x jest zmienną predykcyjną.
a i b są stałymi nazywanymi współczynnikami.

Kroki prowadzące do ustalenia regresji

Prostym przykładem regresji jest przewidywanie wagi osoby, gdy znany jest jej wzrost. Aby to zrobić, musimy mieć związek między wzrostem a wagą osoby.

Kroki do stworzenia relacji to -

Przeprowadź doświadczenie polegające na zebraniu próbki obserwowanych wartości wzrostu i odpowiadającej im wagi.
Utwórz model relacji przy użyciu lm() funkcje w R.
Znajdź współczynniki z utworzonego modelu i utwórz z nich równanie matematyczne
Uzyskaj podsumowanie modelu relacji, aby poznać średni błąd w prognozowaniu. Nazywany równieżresiduals.
Aby przewidzieć wagę nowych osób, użyj predict() funkcja w R.

Dane wejściowe

Poniżej przedstawiono przykładowe dane reprezentujące obserwacje -

# Values of height
151, 174, 138, 186, 128, 136, 179, 163, 152, 131

# Values of weight.
63, 81, 56, 91, 47, 57, 76, 72, 62, 48

Funkcja lm ()

Ta funkcja tworzy model relacji między predyktorem a zmienną odpowiedzi.

Składnia

Podstawowa składnia lm() funkcja w regresji liniowej to -

lm(formula,data)

Poniżej znajduje się opis użytych parametrów -

formula to symbol przedstawiający związek między x i y.
data jest wektorem, na którym zostanie zastosowana formuła.

Utwórz model relacji i uzyskaj współczynniki

x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)

# Apply the lm() function.
relation <- lm(y~x)

print(relation)

Kiedy wykonujemy powyższy kod, daje on następujący wynik -

Call:
lm(formula = y ~ x)

Coefficients:
(Intercept)            x  
   -38.4551          0.6746

Uzyskaj podsumowanie związku

x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)

# Apply the lm() function.
relation <- lm(y~x)

print(summary(relation))

Kiedy wykonujemy powyższy kod, daje on następujący wynik -

Call:
lm(formula = y ~ x)

Residuals:
    Min      1Q     Median      3Q     Max 
-6.3002    -1.6629  0.0412    1.8944  3.9775 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -38.45509    8.04901  -4.778  0.00139 ** 
x             0.67461    0.05191  12.997 1.16e-06 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.253 on 8 degrees of freedom
Multiple R-squared:  0.9548,    Adjusted R-squared:  0.9491 
F-statistic: 168.9 on 1 and 8 DF,  p-value: 1.164e-06

Predict () Funkcja

Składnia

Podstawowa składnia funkcji predykcji () w regresji liniowej to -

predict(object, newdata)

Poniżej znajduje się opis użytych parametrów -

object to formuła, która została już utworzona za pomocą funkcji lm ().
newdata jest wektorem zawierającym nową wartość zmiennej predykcyjnej.

Przewiduj wagę nowych osób

# The predictor vector.
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)

# The resposne vector.
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)

# Apply the lm() function.
relation <- lm(y~x)

# Find weight of a person with height 170.
a <- data.frame(x = 170)
result <-  predict(relation,a)
print(result)

Kiedy wykonujemy powyższy kod, daje on następujący wynik -

1 
76.22869

Wizualizuj regresję graficznie

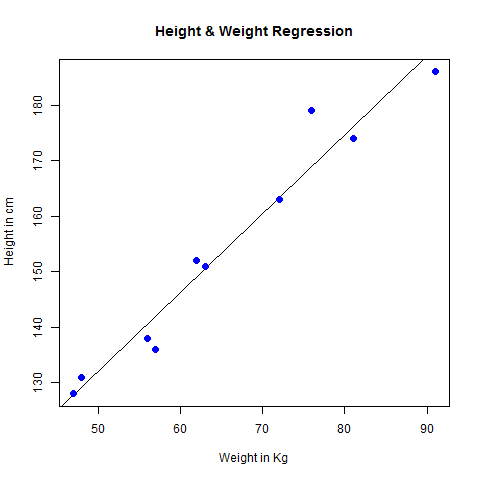
# Create the predictor and response variable.
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
relation <- lm(y~x)

# Give the chart file a name.
png(file = "linearregression.png")

# Plot the chart.
plot(y,x,col = "blue",main = "Height & Weight Regression",
abline(lm(x~y)),cex = 1.3,pch = 16,xlab = "Weight in Kg",ylab = "Height in cm")

# Save the file.
dev.off()

Kiedy wykonujemy powyższy kod, daje on następujący wynik -