R - Szybki przewodnik
R to język programowania i środowisko oprogramowania do analizy statystycznej, reprezentacji graficznej i raportowania. R został stworzony przez Rossa Ihakę i Roberta Gentlemana z University of Auckland w Nowej Zelandii, a obecnie jest rozwijany przez R Development Core Team.
Rdzeniem języka R jest interpretowany język komputerowy, który umożliwia tworzenie rozgałęzień i pętli, a także programowanie modułowe przy użyciu funkcji. R umożliwia integrację z procedurami napisanymi w językach C, C ++, .Net, Python lub FORTRAN w celu zwiększenia wydajności.
R jest dostępny bezpłatnie na podstawie Powszechnej Licencji Publicznej GNU, a wstępnie skompilowane wersje binarne są dostarczane dla różnych systemów operacyjnych, takich jak Linux, Windows i Mac.
R jest wolnym oprogramowaniem rozpowszechnianym na lewej kopii w stylu GNU i oficjalnej części projektu GNU o nazwie GNU S.
Ewolucja R.
R został pierwotnie napisany przez Ross Ihaka i Robert Gentlemanna Wydziale Statystyki Uniwersytetu Auckland w Auckland w Nowej Zelandii. R pojawił się po raz pierwszy w 1993 roku.
Duża grupa osób przyczyniła się do rozwoju języka R, wysyłając kod i raporty o błędach.
Od połowy 1997 roku istnieje grupa podstawowa („R Core Team”), która może modyfikować archiwum kodu źródłowego R.
Funkcje R
Jak wspomniano wcześniej, R to język programowania i środowisko oprogramowania do analizy statystycznej, reprezentacji graficznej i raportowania. Poniżej przedstawiono ważne cechy R -
R jest dobrze rozwiniętym, prostym i skutecznym językiem programowania, który zawiera instrukcje warunkowe, pętle, funkcje rekurencyjne zdefiniowane przez użytkownika oraz funkcje wejścia i wyjścia.
R posiada efektywne zaplecze do przetwarzania i przechowywania danych,
R zapewnia zestaw operatorów do obliczeń na tablicach, listach, wektorach i macierzach.
R zapewnia duży, spójny i zintegrowany zbiór narzędzi do analizy danych.
R zapewnia funkcje graficzne do analizy danych i wyświetlania bezpośrednio na komputerze lub drukowania na papierach.
Podsumowując, R jest najczęściej używanym językiem programowania statystycznego na świecie. Jest to najlepszy wybór analityków danych, wspierany przez dynamiczną i utalentowaną społeczność współtwórców. R jest wykładany na uniwersytetach i wdrażany w krytycznych aplikacjach biznesowych. Ten samouczek nauczy Cię programowania w języku R wraz z odpowiednimi przykładami w prostych i łatwych krokach.
Konfiguracja środowiska lokalnego
Jeśli nadal chcesz skonfigurować swoje środowisko dla języka R, możesz wykonać czynności podane poniżej.
Instalacja systemu Windows
Możesz pobrać wersję R instalatora Windows z R-3.2.2 dla Windows (32/64 bit) i zapisać ją w katalogu lokalnym.
Ponieważ jest to instalator systemu Windows (.exe) o nazwie „R-wersja-win.exe”. Możesz po prostu kliknąć dwukrotnie i uruchomić instalator, akceptując ustawienia domyślne. Jeśli Twój system Windows jest w wersji 32-bitowej, instaluje wersję 32-bitową. Ale jeśli twój system Windows jest 64-bitowy, instaluje zarówno wersję 32-bitową, jak i 64-bitową.
Po instalacji można zlokalizować ikonę uruchamiania programu w strukturze katalogów „R \ R3.2.2 \ bin \ i386 \ Rgui.exe” w folderze Pliki programów systemu Windows. Kliknięcie tej ikony powoduje wyświetlenie R-GUI, czyli konsoli R służącej do programowania języka R.
Instalacja w systemie Linux
R jest dostępny jako plik binarny dla wielu wersji Linuksa w lokalizacji R Binaries .
Instrukcje instalacji Linuksa różnią się w zależności od smaku. Te kroki są wymienione pod każdym typem wersji Linuksa we wspomnianym odnośniku. Jeśli jednak się spieszysz, możesz użyćyum polecenie zainstalowania R w następujący sposób -
$ yum install RPowyższe polecenie zainstaluje podstawową funkcjonalność programowania R wraz ze standardowymi pakietami, nadal potrzebujesz dodatkowego pakietu, a następnie możesz uruchomić monit R w następujący sposób -
$ R
R version 3.2.0 (2015-04-16) -- "Full of Ingredients"
Copyright (C) 2015 The R Foundation for Statistical Computing
Platform: x86_64-redhat-linux-gnu (64-bit)
R is free software and comes with ABSOLUTELY NO WARRANTY.
You are welcome to redistribute it under certain conditions.
Type 'license()' or 'licence()' for distribution details.
R is a collaborative project with many contributors.
Type 'contributors()' for more information and
'citation()' on how to cite R or R packages in publications.
Type 'demo()' for some demos, 'help()' for on-line help, or
'help.start()' for an HTML browser interface to help.
Type 'q()' to quit R.
>Teraz możesz użyć polecenia instalacji w wierszu polecenia R, aby zainstalować wymagany pakiet. Na przykład zainstaluje się następujące polecenieplotrix pakiet wymagany do wykresów 3D.
> install.packages("plotrix")W ramach konwencji zaczniemy uczyć się programowania w języku R od napisania odpowiedzi „Hello, World!” program. W zależności od potrzeb możesz programować w wierszu polecenia R lub możesz użyć pliku skryptu R do napisania programu. Sprawdźmy jedno po drugim.
Wiersz polecenia R.
Po skonfigurowaniu środowiska R łatwo jest uruchomić wiersz polecenia R, wpisując po prostu następujące polecenie w wierszu polecenia -
$ RSpowoduje to uruchomienie interpretera języka R i pojawi się monit>, w którym możesz rozpocząć wpisywanie programu w następujący sposób -
> myString <- "Hello, World!"
> print ( myString)
[1] "Hello, World!"Tutaj pierwsza instrukcja definiuje zmienną łańcuchową myString, do której przypisujemy ciąg „Hello, World!” a następnie następna instrukcja print () jest używana do wydrukowania wartości przechowywanej w zmiennej myString.
Plik skryptu R.
Zazwyczaj programujesz, pisząc programy w plikach skryptów, a następnie wykonujesz te skrypty w wierszu poleceń za pomocą interpretera języka R o nazwie Rscript. Zacznijmy więc od napisania następującego kodu w pliku tekstowym o nazwie test.R jako pod -
# My first program in R Programming
myString <- "Hello, World!"
print ( myString)Zapisz powyższy kod w pliku test.R i wykonaj go w wierszu poleceń Linuksa, jak podano poniżej. Nawet jeśli używasz systemu Windows lub innego systemu, składnia pozostanie taka sama.
$ Rscript test.RKiedy uruchamiamy powyższy program, daje on następujący wynik.
[1] "Hello, World!"Komentarze
Komentarze są jak tekst pomocy w programie R i są ignorowane przez interpreter podczas wykonywania programu. Pojedynczy komentarz jest zapisywany przy użyciu znaku # na początku instrukcji w następujący sposób -
# My first program in R ProgrammingR nie obsługuje komentarzy wieloliniowych, ale możesz wykonać sztuczkę, która jest następująca -
if(FALSE) {
"This is a demo for multi-line comments and it should be put inside either a
single OR double quote"
}
myString <- "Hello, World!"
print ( myString)[1] "Hello, World!"Chociaż powyższe komentarze zostaną wykonane przez interpreter języka R, nie będą one kolidować z rzeczywistym programem. Takie komentarze należy umieszczać w cudzysłowie pojedynczym lub podwójnym.
Generalnie podczas programowania w dowolnym języku programowania należy używać różnych zmiennych do przechowywania różnych informacji. Zmienne to nic innego jak zarezerwowane miejsca w pamięci do przechowywania wartości. Oznacza to, że podczas tworzenia zmiennej rezerwujesz trochę miejsca w pamięci.
Możesz chcieć przechowywać informacje o różnych typach danych, takich jak znak, szeroki znak, liczba całkowita, zmiennoprzecinkowa, podwójna zmiennoprzecinkowa, logiczna itp. Na podstawie typu danych zmiennej system operacyjny przydziela pamięć i decyduje, co może być przechowywane w zarezerwowana pamięć.
W przeciwieństwie do innych języków programowania, takich jak C i java w R, zmienne nie są deklarowane jako jakiś typ danych. Zmiennym przypisywane są obiekty R, a typ danych obiektu R staje się typem danych zmiennej. Istnieje wiele typów obiektów R. Często używane to -
- Vectors
- Lists
- Matrices
- Arrays
- Factors
- Ramki danych
Najprostszym z tych obiektów jest plik vector objecti istnieje sześć typów danych tych wektorów atomowych, określanych również jako sześć klas wektorów. Pozostałe obiekty R są zbudowane na wektorach atomowych.
| Typ danych | Przykład | Zweryfikować |
|---|---|---|
| Logiczny | PRAWDA FAŁSZ |
daje następujący wynik - |
| Numeryczne | 12,3, 5, 999 |
daje następujący wynik - |
| Liczba całkowita | 2L, 34L, 0L |
daje następujący wynik - |
| Złożony | 3 + 2i |
daje następujący wynik - |
| Postać | „a”, „dobry”, „PRAWDA”, „23,4” |
daje następujący wynik - |
| Surowy | „Hello” jest przechowywane jako 48 65 6c 6c 6f |
daje następujący wynik - |
W programowaniu w języku R bardzo podstawowymi typami danych są obiekty R. vectorsktóre zawierają elementy różnych klas, jak pokazano powyżej. Proszę zauważyć, że w R liczba klas nie ogranicza się tylko do powyższych sześciu typów. Na przykład, możemy użyć wielu wektorów atomowych i stworzyć tablicę, której klasa stanie się tablicą.
Wektory
Jeśli chcesz stworzyć wektor z więcej niż jednym elementem, powinieneś użyć c() funkcja, która oznacza połączenie elementów w wektor.
# Create a vector.
apple <- c('red','green',"yellow")
print(apple)
# Get the class of the vector.
print(class(apple))Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] "red" "green" "yellow"
[1] "character"Listy
Lista to obiekt R, który może zawierać wiele różnych typów elementów, takich jak wektory, funkcje, a nawet inną listę wewnątrz siebie.
# Create a list.
list1 <- list(c(2,5,3),21.3,sin)
# Print the list.
print(list1)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[[1]]
[1] 2 5 3
[[2]]
[1] 21.3
[[3]]
function (x) .Primitive("sin")Matryce
Macierz to dwuwymiarowy prostokątny zestaw danych. Można go utworzyć za pomocą wejścia wektorowego do funkcji macierzowej.
# Create a matrix.
M = matrix( c('a','a','b','c','b','a'), nrow = 2, ncol = 3, byrow = TRUE)
print(M)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[,1] [,2] [,3]
[1,] "a" "a" "b"
[2,] "c" "b" "a"Tablice
Podczas gdy macierze są ograniczone do dwóch wymiarów, tablice mogą mieć dowolną liczbę wymiarów. Funkcja tablicowa przyjmuje atrybut dim, który tworzy wymaganą liczbę wymiarów. W poniższym przykładzie tworzymy tablicę z dwoma elementami, z których każdy jest macierzą 3x3.
# Create an array.
a <- array(c('green','yellow'),dim = c(3,3,2))
print(a)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
, , 1
[,1] [,2] [,3]
[1,] "green" "yellow" "green"
[2,] "yellow" "green" "yellow"
[3,] "green" "yellow" "green"
, , 2
[,1] [,2] [,3]
[1,] "yellow" "green" "yellow"
[2,] "green" "yellow" "green"
[3,] "yellow" "green" "yellow"Czynniki
Czynniki to r-obiekty utworzone za pomocą wektora. Przechowuje wektor wraz z różnymi wartościami elementów w wektorze jako etykiety. Etykiety są zawsze znakowe, niezależnie od tego, czy w wektorze wejściowym są numeryczne, czy też znakowe, logiczne itp. Są przydatne w modelowaniu statystycznym.
Czynniki są tworzone przy użyciu factor()funkcjonować. Pliknlevels funkcje podaje liczbę poziomów.
# Create a vector.
apple_colors <- c('green','green','yellow','red','red','red','green')
# Create a factor object.
factor_apple <- factor(apple_colors)
# Print the factor.
print(factor_apple)
print(nlevels(factor_apple))Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] green green yellow red red red green
Levels: green red yellow
[1] 3Ramki danych
Ramki danych to tabelaryczne obiekty danych. W przeciwieństwie do macierzy w ramce danych, każda kolumna może zawierać różne tryby danych. Pierwsza kolumna może być numeryczna, druga kolumna może być znakowa, a trzecia kolumna może być logiczna. Jest to lista wektorów o równej długości.
Ramki danych są tworzone przy użyciu rozszerzenia data.frame() funkcjonować.
# Create the data frame.
BMI <- data.frame(
gender = c("Male", "Male","Female"),
height = c(152, 171.5, 165),
weight = c(81,93, 78),
Age = c(42,38,26)
)
print(BMI)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
gender height weight Age
1 Male 152.0 81 42
2 Male 171.5 93 38
3 Female 165.0 78 26Zmienna zapewnia nam nazwane miejsce do przechowywania, którym nasze programy mogą manipulować. Zmienna w R może przechowywać wektor atomowy, grupę wektorów atomowych lub kombinację wielu obiektów Robject. Prawidłowa nazwa zmiennej składa się z liter, cyfr oraz kropki lub podkreślenia. Nazwa zmiennej zaczyna się od litery lub kropki, po której nie następuje cyfra.
| Nazwa zmiennej | Ważność | Powód |
|---|---|---|
| nazwa_zmiennej2. | ważny | Zawiera litery, cyfry, kropkę i podkreślenie |
| var_name% | Nieważny | Ma znak „%”. Dozwolone są tylko kropki (.) I podkreślenia. |
| 2var_name | nieważny | Rozpoczyna się liczbą |
.var_name, var.name |
ważny | Może zaczynać się od kropki (.), Ale po kropce (.) Nie powinna następować liczba. |
| .2var_name | nieważny | Po kropce początkowej następuje liczba, która czyni ją nieważną. |
| _var_name | nieważny | Zaczyna się od _, który jest nieprawidłowy |
Przypisanie zmiennej
Zmiennym można przypisać wartości przy użyciu operatora w lewo, w prawo i równości. Wartości zmiennych można wydrukować za pomocąprint() lub cat()funkcjonować. Plikcat() funkcja łączy wiele elementów w ciągły wydruk.
# Assignment using equal operator.
var.1 = c(0,1,2,3)
# Assignment using leftward operator.
var.2 <- c("learn","R")
# Assignment using rightward operator.
c(TRUE,1) -> var.3
print(var.1)
cat ("var.1 is ", var.1 ,"\n")
cat ("var.2 is ", var.2 ,"\n")
cat ("var.3 is ", var.3 ,"\n")Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] 0 1 2 3
var.1 is 0 1 2 3
var.2 is learn R
var.3 is 1 1Note- Wektor c (TRUE, 1) jest połączeniem klasy logicznej i numerycznej. Tak więc klasa logiczna jest wymuszana na klasę numeryczną, dzięki czemu PRAWDA jest równa 1.
Typ danych zmiennej
W języku R sama zmienna nie jest zadeklarowana dla żadnego typu danych, a raczej pobiera typ danych przypisanego do niej obiektu R. Tak więc R jest nazywany językiem z typami dynamicznymi, co oznacza, że możemy wielokrotnie zmieniać typ danych tej samej zmiennej, gdy używamy jej w programie.
var_x <- "Hello"
cat("The class of var_x is ",class(var_x),"\n")
var_x <- 34.5
cat(" Now the class of var_x is ",class(var_x),"\n")
var_x <- 27L
cat(" Next the class of var_x becomes ",class(var_x),"\n")Kiedy wykonujemy powyższy kod, daje on następujący wynik -
The class of var_x is character
Now the class of var_x is numeric
Next the class of var_x becomes integerZnajdowanie zmiennych
Aby poznać wszystkie zmienne aktualnie dostępne w obszarze roboczym, używamy ls()funkcjonować. Również funkcja ls () może używać wzorców do dopasowywania nazw zmiennych.
print(ls())Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] "my var" "my_new_var" "my_var" "var.1"
[5] "var.2" "var.3" "var.name" "var_name2."
[9] "var_x" "varname"Note - To jest przykładowe wyjście zależne od tego, jakie zmienne są zadeklarowane w twoim środowisku.
Funkcja ls () może używać wzorców do dopasowywania nazw zmiennych.
# List the variables starting with the pattern "var".
print(ls(pattern = "var"))Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] "my var" "my_new_var" "my_var" "var.1"
[5] "var.2" "var.3" "var.name" "var_name2."
[9] "var_x" "varname"Zmienne zaczynające się od dot(.) są ukryte, można je wyświetlić przy użyciu argumentu "all.names = TRUE" funkcji ls ().
print(ls(all.name = TRUE))Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] ".cars" ".Random.seed" ".var_name" ".varname" ".varname2"
[6] "my var" "my_new_var" "my_var" "var.1" "var.2"
[11]"var.3" "var.name" "var_name2." "var_x"Usuwanie zmiennych
Zmienne można usuwać za pomocą rozszerzenia rm()funkcjonować. Poniżej usuwamy zmienną var.3. Podczas drukowania wartość zmiennej jest wyrzucana błąd.
rm(var.3)
print(var.3)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] "var.3"
Error in print(var.3) : object 'var.3' not foundWszystkie zmienne można usunąć za pomocą rm() i ls() funkcjonować razem.
rm(list = ls())
print(ls())Kiedy wykonujemy powyższy kod, daje on następujący wynik -
character(0)Operator to symbol, który mówi kompilatorowi, aby wykonał określone operacje matematyczne lub logiczne. Język R jest bogaty we wbudowane operatory i zapewnia następujące typy operatorów.
Rodzaje operatorów
W programowaniu R mamy następujące typy operatorów -
- Operatory arytmetyczne
- Operatorzy relacyjni
- Operatory logiczne
- Operatory przypisania
- Różni operatorzy
Operatory arytmetyczne
Poniższa tabela przedstawia operatory arytmetyczne obsługiwane przez język R. Operatory działają na każdym elemencie wektora.
| Operator | Opis | Przykład |
|---|---|---|
| + | Dodaje dwa wektory |
daje następujący wynik - |
| - | Odejmuje drugi wektor od pierwszego |
daje następujący wynik - |
| * | Mnoży oba wektory |
daje następujący wynik - |
| / | Podziel pierwszy wektor z drugim |
Kiedy wykonujemy powyższy kod, daje on następujący wynik - |
| %% | Resztę pierwszego wektora podaj drugiemu |
daje następujący wynik - |
| % /% | Wynik dzielenia pierwszego wektora przez drugi (iloraz) |
daje następujący wynik - |
| ^ | Pierwszy wektor podniesiony do wykładnika drugiego wektora |
daje następujący wynik - |
Operatorzy relacyjni
Poniższa tabela przedstawia operatory relacyjne obsługiwane przez język R. Każdy element pierwszego wektora jest porównywany z odpowiadającym mu elementem drugiego wektora. Wynikiem porównania jest wartość logiczna.
| Operator | Opis | Przykład |
|---|---|---|
| > | Sprawdza, czy każdy element pierwszego wektora jest większy niż odpowiadający element drugiego wektora. |
daje następujący wynik - |
| < | Sprawdza, czy każdy element pierwszego wektora jest mniejszy niż odpowiadający mu element drugiego wektora. |
daje następujący wynik - |
| == | Sprawdza, czy każdy element pierwszego wektora jest równy odpowiadającemu elementowi drugiego wektora. |
daje następujący wynik - |
| <= | Sprawdza, czy każdy element pierwszego wektora jest mniejszy lub równy odpowiadającemu elementowi drugiego wektora. |
daje następujący wynik - |
| > = | Sprawdza, czy każdy element pierwszego wektora jest większy lub równy odpowiadającemu elementowi drugiego wektora. |
daje następujący wynik - |
| ! = | Sprawdza, czy każdy element pierwszego wektora jest nierówny z odpowiadającym mu elementem drugiego wektora. |
daje następujący wynik - |
Operatory logiczne
Poniższa tabela przedstawia operatory logiczne obsługiwane przez język R. Ma zastosowanie tylko do wektorów typu logicznego, numerycznego lub złożonego. Wszystkie liczby większe niż 1 są traktowane jako wartość logiczna PRAWDA.
Każdy element pierwszego wektora jest porównywany z odpowiadającym mu elementem drugiego wektora. Wynikiem porównania jest wartość logiczna.
| Operator | Opis | Przykład |
|---|---|---|
| & | Nazywa się to operatorem logicznym AND w odniesieniu do elementów. Łączy każdy element pierwszego wektora z odpowiednim elementem drugiego wektora i daje wynik PRAWDA, jeśli oba elementy są PRAWDA. |
daje następujący wynik - |
| | | Nazywa się to operatorem logicznym OR opartym na elementach. Łączy każdy element pierwszego wektora z odpowiednim elementem drugiego wektora i daje wynik PRAWDA, jeśli jeden z elementów ma wartość PRAWDA. |
daje następujący wynik - |
| ! | Nazywa się to operatorem logicznym NOT. Pobiera każdy element wektora i podaje przeciwną wartość logiczną. |
daje następujący wynik - |
Operator logiczny && i || bierze pod uwagę tylko pierwszy element wektorów i podaje wektor pojedynczego elementu jako wynik.
| Operator | Opis | Przykład |
|---|---|---|
| && | Nazywany operatorem logicznym AND. Pobiera pierwszy element obu wektorów i podaje PRAWDA tylko wtedy, gdy oba są PRAWDA. |
daje następujący wynik - |
| || | Nazywany operatorem logicznym OR. Pobiera pierwszy element obu wektorów i podaje PRAWDA, jeśli jeden z nich jest PRAWDA. |
daje następujący wynik - |
Operatory przypisania
Te operatory służą do przypisywania wartości do wektorów.
| Operator | Opis | Przykład |
|---|---|---|
| <- lub = lub << - |
Nazywa się przydział lewostronny |
daje następujący wynik - |
| -> lub - >> |
Nazywa się Przypisanie Praw |
daje następujący wynik - |
Różni operatorzy
Operatory te są używane do określonego celu, a nie do ogólnych obliczeń matematycznych lub logicznych.
| Operator | Opis | Przykład |
|---|---|---|
| : | Operator okrężnicy. Tworzy serię liczb w sekwencji dla wektora. |
daje następujący wynik - |
| %w% | Ten operator służy do identyfikacji, czy element należy do wektora. |
daje następujący wynik - |
| % *% | Ten operator służy do mnożenia macierzy z jej transpozycją. |
daje następujący wynik - |
Struktury decyzyjne wymagają od programisty określenia jednego lub więcej warunków, które mają być ocenione lub przetestowane przez program, wraz z instrukcją lub instrukcjami do wykonania, jeśli warunek zostanie określony jako truei opcjonalnie inne instrukcje do wykonania, jeśli warunek zostanie określony false.
Poniżej przedstawiono ogólną formę typowej struktury podejmowania decyzji występującej w większości języków programowania -
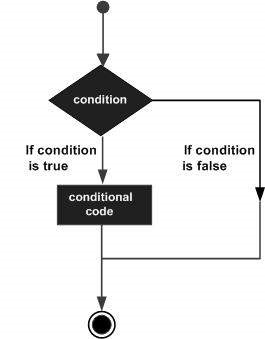
R zapewnia następujące typy oświadczeń decyzyjnych. Kliknij poniższe łącza, aby sprawdzić ich szczegóły.
| Sr.No. | Oświadczenie i opis |
|---|---|
| 1 | jeśli oświadczenie Na if instrukcja składa się z wyrażenia logicznego, po którym następuje co najmniej jedna instrukcja. |
| 2 | if ... else oświadczenie Na if po instrukcji może następować opcjonalne else instrukcja, która jest wykonywana, gdy wyrażenie logiczne jest fałszywe. |
| 3 | instrukcja przełączania ZA switch Instrukcja umożliwia testowanie zmiennej pod kątem równości względem listy wartości. |
Może zaistnieć sytuacja, w której trzeba będzie kilkakrotnie wykonać blok kodu. Ogólnie instrukcje są wykonywane sekwencyjnie. Pierwsza instrukcja funkcji jest wykonywana jako pierwsza, po niej następuje druga i tak dalej.
Języki programowania zapewniają różne struktury kontrolne, które pozwalają na bardziej skomplikowane ścieżki wykonywania.
Instrukcja pętli pozwala nam wielokrotnie wykonać instrukcję lub grupę instrukcji, a poniżej przedstawiono ogólną postać instrukcji pętli w większości języków programowania:
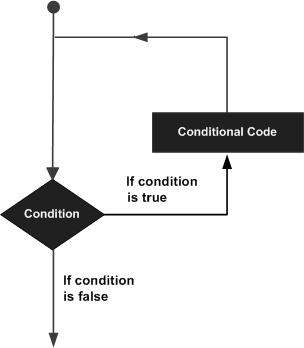
Język programowania R udostępnia następujące rodzaje pętli do obsługi wymagań dotyczących pętli. Kliknij poniższe łącza, aby sprawdzić ich szczegóły.
| Sr.No. | Typ i opis pętli |
|---|---|
| 1 | powtórz pętlę Wykonuje sekwencję instrukcji wiele razy i skraca kod zarządzający zmienną pętli. |
| 2 | pętla while Powtarza instrukcję lub grupę instrukcji, gdy dany warunek jest prawdziwy. Testuje warunek przed wykonaniem treści pętli. |
| 3 | dla pętli Podobnie jak instrukcja while, z tą różnicą, że testuje warunek na końcu treści pętli. |
Instrukcje sterowania pętlą
Instrukcje sterujące pętlą zmieniają wykonanie z jego normalnej sekwencji. Gdy wykonanie opuszcza zakres, wszystkie automatyczne obiekty utworzone w tym zakresie są niszczone.
R obsługuje następujące instrukcje sterujące. Kliknij poniższe łącza, aby sprawdzić ich szczegóły.
| Sr.No. | Oświadczenie i opis kontroli |
|---|---|
| 1 | instrukcja break Kończy loop instrukcja i przekazuje wykonanie instrukcji bezpośrednio po pętli. |
| 2 | Następne oświadczenie Plik next instrukcja symuluje zachowanie przełącznika R. |
Funkcja to zestaw instrukcji zorganizowanych razem w celu wykonania określonego zadania. R ma dużą liczbę wbudowanych funkcji, a użytkownik może tworzyć własne funkcje.
W języku R funkcja jest obiektem, więc interpreter języka R jest w stanie przekazać kontrolę do funkcji wraz z argumentami, które mogą być konieczne, aby funkcja mogła wykonać działania.
Funkcja z kolei wykonuje swoje zadanie i zwraca kontrolę interpreterowi, jak również wszelkie wyniki, które mogą być przechowywane w innych obiektach.
Definicja funkcji
Funkcja R jest tworzona za pomocą słowa kluczowego function. Podstawowa składnia definicji funkcji R jest następująca -
function_name <- function(arg_1, arg_2, ...) {
Function body
}Komponenty funkcyjne
Różne części funkcji to -
Function Name- To jest rzeczywista nazwa funkcji. Jest przechowywany w środowisku R jako obiekt o tej nazwie.
Arguments- Argument jest symbolem zastępczym. Kiedy funkcja jest wywoływana, przekazujesz wartość do argumentu. Argumenty są opcjonalne; to znaczy, funkcja może nie zawierać żadnych argumentów. Również argumenty mogą mieć wartości domyślne.
Function Body - Treść funkcji zawiera zbiór instrukcji, które definiują, co robi funkcja.
Return Value - Wartość zwracana funkcji to ostatnie wyrażenie w treści funkcji, które ma zostać ocenione.
R ma wiele in-builtfunkcje, które można wywołać bezpośrednio w programie bez ich wcześniejszego definiowania. Możemy również tworzyć i wykorzystywać własne funkcje, tzwuser defined Funkcje.
Wbudowana funkcja
Proste przykłady wbudowanych funkcji to seq(), mean(), max(), sum(x) i paste(...)itd. Są one wywoływane bezpośrednio przez programy napisane przez użytkownika. Możesz odwołać się do najczęściej używanych funkcji R.
# Create a sequence of numbers from 32 to 44.
print(seq(32,44))
# Find mean of numbers from 25 to 82.
print(mean(25:82))
# Find sum of numbers frm 41 to 68.
print(sum(41:68))Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] 32 33 34 35 36 37 38 39 40 41 42 43 44
[1] 53.5
[1] 1526Funkcja zdefiniowana przez użytkownika
Możemy tworzyć funkcje zdefiniowane przez użytkownika w R. Są one specyficzne dla tego, czego chce użytkownik, a po utworzeniu mogą być używane jak funkcje wbudowane. Poniżej znajduje się przykład tworzenia i używania funkcji.
# Create a function to print squares of numbers in sequence.
new.function <- function(a) {
for(i in 1:a) {
b <- i^2
print(b)
}
}Wywołanie funkcji
# Create a function to print squares of numbers in sequence.
new.function <- function(a) {
for(i in 1:a) {
b <- i^2
print(b)
}
}
# Call the function new.function supplying 6 as an argument.
new.function(6)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] 1
[1] 4
[1] 9
[1] 16
[1] 25
[1] 36Wywołanie funkcji bez argumentu
# Create a function without an argument.
new.function <- function() {
for(i in 1:5) {
print(i^2)
}
}
# Call the function without supplying an argument.
new.function()Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] 1
[1] 4
[1] 9
[1] 16
[1] 25Wywołanie funkcji z wartościami argumentów (według pozycji i nazwy)
Argumenty wywołania funkcji mogą być podawane w tej samej kolejności, jak zdefiniowano w funkcji, lub mogą być dostarczane w innej kolejności, ale przypisane do nazw argumentów.
# Create a function with arguments.
new.function <- function(a,b,c) {
result <- a * b + c
print(result)
}
# Call the function by position of arguments.
new.function(5,3,11)
# Call the function by names of the arguments.
new.function(a = 11, b = 5, c = 3)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] 26
[1] 58Wywołanie funkcji z argumentem domyślnym
Możemy zdefiniować wartość argumentów w definicji funkcji i wywołać funkcję bez podawania żadnego argumentu, aby uzyskać domyślny wynik. Ale możemy również wywołać takie funkcje, podając nowe wartości argumentu i otrzymując wynik inny niż domyślny.
# Create a function with arguments.
new.function <- function(a = 3, b = 6) {
result <- a * b
print(result)
}
# Call the function without giving any argument.
new.function()
# Call the function with giving new values of the argument.
new.function(9,5)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] 18
[1] 45Leniwa ocena funkcji
Argumenty funkcji są obliczane leniwie, co oznacza, że są oceniane tylko wtedy, gdy jest to wymagane przez treść funkcji.
# Create a function with arguments.
new.function <- function(a, b) {
print(a^2)
print(a)
print(b)
}
# Evaluate the function without supplying one of the arguments.
new.function(6)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] 36
[1] 6
Error in print(b) : argument "b" is missing, with no defaultKażda wartość zapisana w parze pojedynczego cudzysłowu lub podwójnego cudzysłowu w R jest traktowana jako ciąg. Wewnętrznie R przechowuje każdy ciąg w cudzysłowach, nawet jeśli tworzysz je za pomocą pojedynczego cudzysłowu.
Reguły stosowane w konstrukcji łańcuchów
Cudzysłowy na początku i na końcu łańcucha powinny być podwójnymi cudzysłowami lub pojedynczymi cudzysłowami. Nie można ich mieszać.
Podwójne cudzysłowy można wstawiać do ciągu znaków rozpoczynającego się i kończącego pojedynczym cudzysłowem.
Pojedynczy cudzysłów można wstawić do ciągu zaczynającego się i kończącego cudzysłowami.
Podwójnych cudzysłowów nie można wstawiać do ciągu znaków rozpoczynającego się i kończącego cudzysłowami.
Pojedynczego cudzysłowu nie można wstawić do ciągu rozpoczynającego się i kończącego pojedynczym cudzysłowem.
Przykłady prawidłowych ciągów
Poniższe przykłady wyjaśniają zasady tworzenia łańcucha w R.
a <- 'Start and end with single quote'
print(a)
b <- "Start and end with double quotes"
print(b)
c <- "single quote ' in between double quotes"
print(c)
d <- 'Double quotes " in between single quote'
print(d)Po uruchomieniu powyższego kodu otrzymujemy następujące dane wyjściowe -
[1] "Start and end with single quote"
[1] "Start and end with double quotes"
[1] "single quote ' in between double quote"
[1] "Double quote \" in between single quote"Przykłady nieprawidłowych ciągów
e <- 'Mixed quotes"
print(e)
f <- 'Single quote ' inside single quote'
print(f)
g <- "Double quotes " inside double quotes"
print(g)Kiedy uruchamiamy skrypt, nie daje on wyników poniżej.
Error: unexpected symbol in:
"print(e)
f <- 'Single"
Execution haltedManipulacja strunami
Concatenating Strings - funkcja paste ()
Wiele ciągów w R jest łączonych za pomocą paste()funkcjonować. Połączenie może wymagać dowolnej liczby argumentów.
Składnia
Podstawowa składnia funkcji wklejania to -
paste(..., sep = " ", collapse = NULL)Poniżej znajduje się opis użytych parametrów -
... reprezentuje dowolną liczbę argumentów do połączenia.
sepreprezentuje dowolny separator między argumentami. Jest to opcjonalne.
collapsesłuży do wyeliminowania odstępu między dwoma ciągami. Ale nie spacja w dwóch słowach jednego ciągu.
Przykład
a <- "Hello"
b <- 'How'
c <- "are you? "
print(paste(a,b,c))
print(paste(a,b,c, sep = "-"))
print(paste(a,b,c, sep = "", collapse = ""))Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] "Hello How are you? "
[1] "Hello-How-are you? "
[1] "HelloHoware you? "Formatowanie liczb i ciągów - funkcja format ()
Liczby i ciągi można sformatować zgodnie z określonym stylem za pomocą format() funkcjonować.
Składnia
Podstawowa składnia funkcji formatu to -
format(x, digits, nsmall, scientific, width, justify = c("left", "right", "centre", "none"))Poniżej znajduje się opis użytych parametrów -
x jest wejściem wektorowym.
digits to całkowita liczba wyświetlanych cyfr.
nsmall to minimalna liczba cyfr po prawej stronie przecinka dziesiętnego.
scientific ma wartość TRUE, aby wyświetlić notację naukową.
width wskazuje minimalną szerokość, która ma być wyświetlana przez wypełnienie spacjami na początku.
justify jest wyświetlaniem ciągu z lewej, prawej lub ze środka.
Przykład
# Total number of digits displayed. Last digit rounded off.
result <- format(23.123456789, digits = 9)
print(result)
# Display numbers in scientific notation.
result <- format(c(6, 13.14521), scientific = TRUE)
print(result)
# The minimum number of digits to the right of the decimal point.
result <- format(23.47, nsmall = 5)
print(result)
# Format treats everything as a string.
result <- format(6)
print(result)
# Numbers are padded with blank in the beginning for width.
result <- format(13.7, width = 6)
print(result)
# Left justify strings.
result <- format("Hello", width = 8, justify = "l")
print(result)
# Justfy string with center.
result <- format("Hello", width = 8, justify = "c")
print(result)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] "23.1234568"
[1] "6.000000e+00" "1.314521e+01"
[1] "23.47000"
[1] "6"
[1] " 13.7"
[1] "Hello "
[1] " Hello "Zliczanie liczby znaków w łańcuchu - funkcja nchar ()
Ta funkcja zlicza liczbę znaków łącznie ze spacjami w ciągu.
Składnia
Podstawowa składnia funkcji nchar () to -
nchar(x)Poniżej znajduje się opis użytych parametrów -
x jest wejściem wektorowym.
Przykład
result <- nchar("Count the number of characters")
print(result)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] 30Zmiana wielkości liter - funkcje toupper () i tolower ()
Te funkcje zmieniają wielkość liter w ciągu znaków.
Składnia
Podstawowa składnia funkcji toupper () i tolower () to -
toupper(x)
tolower(x)Poniżej znajduje się opis użytych parametrów -
x jest wejściem wektorowym.
Przykład
# Changing to Upper case.
result <- toupper("Changing To Upper")
print(result)
# Changing to lower case.
result <- tolower("Changing To Lower")
print(result)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] "CHANGING TO UPPER"
[1] "changing to lower"Wyodrębnianie części ciągu - funkcja substring ()
Ta funkcja wyodrębnia części ciągu.
Składnia
Podstawowa składnia funkcji substring () to -
substring(x,first,last)Poniżej znajduje się opis użytych parametrów -
x jest wejściem wektora znakowego.
first to pozycja pierwszego wyodrębnionego znaku.
last to pozycja ostatniego wyodrębnionego znaku.
Przykład
# Extract characters from 5th to 7th position.
result <- substring("Extract", 5, 7)
print(result)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] "act"Wektory to najbardziej podstawowe obiekty danych R i istnieje sześć typów wektorów atomowych. Są logiczne, całkowite, podwójne, złożone, znakowe i surowe.
Tworzenie wektorów
Pojedynczy element wektora
Nawet jeśli napiszesz tylko jedną wartość w R, stanie się ona wektorem o długości 1 i należy do jednego z powyższych typów wektorów.
# Atomic vector of type character.
print("abc");
# Atomic vector of type double.
print(12.5)
# Atomic vector of type integer.
print(63L)
# Atomic vector of type logical.
print(TRUE)
# Atomic vector of type complex.
print(2+3i)
# Atomic vector of type raw.
print(charToRaw('hello'))Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] "abc"
[1] 12.5
[1] 63
[1] TRUE
[1] 2+3i
[1] 68 65 6c 6c 6fWektor wielu elementów
Using colon operator with numeric data
# Creating a sequence from 5 to 13.
v <- 5:13
print(v)
# Creating a sequence from 6.6 to 12.6.
v <- 6.6:12.6
print(v)
# If the final element specified does not belong to the sequence then it is discarded.
v <- 3.8:11.4
print(v)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] 5 6 7 8 9 10 11 12 13
[1] 6.6 7.6 8.6 9.6 10.6 11.6 12.6
[1] 3.8 4.8 5.8 6.8 7.8 8.8 9.8 10.8Using sequence (Seq.) operator
# Create vector with elements from 5 to 9 incrementing by 0.4.
print(seq(5, 9, by = 0.4))Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] 5.0 5.4 5.8 6.2 6.6 7.0 7.4 7.8 8.2 8.6 9.0Using the c() function
Wartości niebędące znakami są przekształcane do typu znakowego, jeśli jeden z elementów jest znakiem.
# The logical and numeric values are converted to characters.
s <- c('apple','red',5,TRUE)
print(s)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] "apple" "red" "5" "TRUE"Dostęp do elementów wektora
Dostęp do elementów wektora uzyskuje się za pomocą indeksowania. Plik[ ] bracketssą używane do indeksowania. Indeksowanie rozpoczyna się od pozycji 1. Podanie wartości ujemnej w indeksie powoduje usunięcie tego elementu z wyniku.TRUE, FALSE lub 0 i 1 może być również używany do indeksowania.
# Accessing vector elements using position.
t <- c("Sun","Mon","Tue","Wed","Thurs","Fri","Sat")
u <- t[c(2,3,6)]
print(u)
# Accessing vector elements using logical indexing.
v <- t[c(TRUE,FALSE,FALSE,FALSE,FALSE,TRUE,FALSE)]
print(v)
# Accessing vector elements using negative indexing.
x <- t[c(-2,-5)]
print(x)
# Accessing vector elements using 0/1 indexing.
y <- t[c(0,0,0,0,0,0,1)]
print(y)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] "Mon" "Tue" "Fri"
[1] "Sun" "Fri"
[1] "Sun" "Tue" "Wed" "Fri" "Sat"
[1] "Sun"Manipulacja wektorami
Arytmetyka wektorów
Można dodać, odjąć, pomnożyć lub podzielić dwa wektory o tej samej długości, uzyskując wynik jako wektor wyjściowy.
# Create two vectors.
v1 <- c(3,8,4,5,0,11)
v2 <- c(4,11,0,8,1,2)
# Vector addition.
add.result <- v1+v2
print(add.result)
# Vector subtraction.
sub.result <- v1-v2
print(sub.result)
# Vector multiplication.
multi.result <- v1*v2
print(multi.result)
# Vector division.
divi.result <- v1/v2
print(divi.result)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] 7 19 4 13 1 13
[1] -1 -3 4 -3 -1 9
[1] 12 88 0 40 0 22
[1] 0.7500000 0.7272727 Inf 0.6250000 0.0000000 5.5000000Recykling elementu wektorowego
Jeśli zastosujemy operacje arytmetyczne do dwóch wektorów o różnej długości, wówczas elementy krótszego wektora są przetwarzane w celu zakończenia operacji.
v1 <- c(3,8,4,5,0,11)
v2 <- c(4,11)
# V2 becomes c(4,11,4,11,4,11)
add.result <- v1+v2
print(add.result)
sub.result <- v1-v2
print(sub.result)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] 7 19 8 16 4 22
[1] -1 -3 0 -6 -4 0Sortowanie elementów wektorowych
Elementy w wektorze można sortować za pomocą sort() funkcjonować.
v <- c(3,8,4,5,0,11, -9, 304)
# Sort the elements of the vector.
sort.result <- sort(v)
print(sort.result)
# Sort the elements in the reverse order.
revsort.result <- sort(v, decreasing = TRUE)
print(revsort.result)
# Sorting character vectors.
v <- c("Red","Blue","yellow","violet")
sort.result <- sort(v)
print(sort.result)
# Sorting character vectors in reverse order.
revsort.result <- sort(v, decreasing = TRUE)
print(revsort.result)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] -9 0 3 4 5 8 11 304
[1] 304 11 8 5 4 3 0 -9
[1] "Blue" "Red" "violet" "yellow"
[1] "yellow" "violet" "Red" "Blue"Listy to obiekty R, które zawierają elementy różnych typów, takie jak - liczby, ciągi znaków, wektory i inna lista wewnątrz nich. Lista może również zawierać macierz lub funkcję jako jej elementy. Lista jest tworzona za pomocąlist() funkcjonować.
Tworzenie listy
Poniżej znajduje się przykład tworzenia listy zawierającej ciągi, liczby, wektory i wartości logiczne.
# Create a list containing strings, numbers, vectors and a logical
# values.
list_data <- list("Red", "Green", c(21,32,11), TRUE, 51.23, 119.1)
print(list_data)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[[1]]
[1] "Red"
[[2]]
[1] "Green"
[[3]]
[1] 21 32 11
[[4]]
[1] TRUE
[[5]]
[1] 51.23
[[6]]
[1] 119.1Nazewnictwo elementów listy
Elementom listy można nadać nazwy i można uzyskać do nich dostęp przy użyciu tych nazw.
# Create a list containing a vector, a matrix and a list.
list_data <- list(c("Jan","Feb","Mar"), matrix(c(3,9,5,1,-2,8), nrow = 2),
list("green",12.3))
# Give names to the elements in the list.
names(list_data) <- c("1st Quarter", "A_Matrix", "A Inner list")
# Show the list.
print(list_data)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
$`1st_Quarter` [1] "Jan" "Feb" "Mar" $A_Matrix
[,1] [,2] [,3]
[1,] 3 5 -2
[2,] 9 1 8
$A_Inner_list $A_Inner_list[[1]]
[1] "green"
$A_Inner_list[[2]]
[1] 12.3Dostęp do elementów listy
Dostęp do elementów listy można uzyskać za pomocą indeksu elementu na liście. W przypadku list nazwanych można uzyskać do niego dostęp również za pomocą nazw.
Nadal używamy listy w powyższym przykładzie -
# Create a list containing a vector, a matrix and a list.
list_data <- list(c("Jan","Feb","Mar"), matrix(c(3,9,5,1,-2,8), nrow = 2),
list("green",12.3))
# Give names to the elements in the list.
names(list_data) <- c("1st Quarter", "A_Matrix", "A Inner list")
# Access the first element of the list.
print(list_data[1])
# Access the thrid element. As it is also a list, all its elements will be printed.
print(list_data[3])
# Access the list element using the name of the element.
print(list_data$A_Matrix)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
$`1st_Quarter` [1] "Jan" "Feb" "Mar" $A_Inner_list
$A_Inner_list[[1]] [1] "green" $A_Inner_list[[2]]
[1] 12.3
[,1] [,2] [,3]
[1,] 3 5 -2
[2,] 9 1 8Manipulowanie elementami listy
Możemy dodawać, usuwać i aktualizować elementy listy, jak pokazano poniżej. Dodawać i usuwać elementy możemy tylko na końcu listy. Ale możemy zaktualizować dowolny element.
# Create a list containing a vector, a matrix and a list.
list_data <- list(c("Jan","Feb","Mar"), matrix(c(3,9,5,1,-2,8), nrow = 2),
list("green",12.3))
# Give names to the elements in the list.
names(list_data) <- c("1st Quarter", "A_Matrix", "A Inner list")
# Add element at the end of the list.
list_data[4] <- "New element"
print(list_data[4])
# Remove the last element.
list_data[4] <- NULL
# Print the 4th Element.
print(list_data[4])
# Update the 3rd Element.
list_data[3] <- "updated element"
print(list_data[3])Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[[1]]
[1] "New element"
$<NA> NULL $`A Inner list`
[1] "updated element"Łączenie list
Możesz połączyć wiele list w jedną listę, umieszczając wszystkie listy wewnątrz jednej funkcji list ().
# Create two lists.
list1 <- list(1,2,3)
list2 <- list("Sun","Mon","Tue")
# Merge the two lists.
merged.list <- c(list1,list2)
# Print the merged list.
print(merged.list)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[[1]]
[1] 1
[[2]]
[1] 2
[[3]]
[1] 3
[[4]]
[1] "Sun"
[[5]]
[1] "Mon"
[[6]]
[1] "Tue"Konwersja listy do wektora
Listę można przekonwertować na wektor, dzięki czemu elementy wektora mogą być użyte do dalszej manipulacji. Wszystkie działania arytmetyczne na wektorach można zastosować po przekonwertowaniu listy na wektory. Aby wykonać tę konwersję, używamy rozszerzeniaunlist()funkcjonować. Pobiera listę jako dane wejściowe i tworzy wektor.
# Create lists.
list1 <- list(1:5)
print(list1)
list2 <-list(10:14)
print(list2)
# Convert the lists to vectors.
v1 <- unlist(list1)
v2 <- unlist(list2)
print(v1)
print(v2)
# Now add the vectors
result <- v1+v2
print(result)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[[1]]
[1] 1 2 3 4 5
[[1]]
[1] 10 11 12 13 14
[1] 1 2 3 4 5
[1] 10 11 12 13 14
[1] 11 13 15 17 19Macierze to obiekty R, w których elementy są rozmieszczone w dwuwymiarowym układzie prostokątnym. Zawierają elementy tego samego typu atomowego. Chociaż możemy stworzyć macierz zawierającą tylko znaki lub tylko wartości logiczne, nie są one zbyt przydatne. Używamy macierzy zawierających elementy numeryczne do wykorzystania w obliczeniach matematycznych.
Matrix jest tworzony przy użyciu matrix() funkcjonować.
Składnia
Podstawowa składnia tworzenia macierzy w R to -
matrix(data, nrow, ncol, byrow, dimnames)Poniżej znajduje się opis użytych parametrów -
data jest wektorem wejściowym, który staje się elementami danych macierzy.
nrow to liczba wierszy do utworzenia.
ncol to liczba kolumn do utworzenia.
byrowto logiczna wskazówka. Jeśli PRAWDA, to elementy wektora wejściowego są uporządkowane według wierszy.
dimname to nazwy przypisane do wierszy i kolumn.
Przykład
Utwórz macierz, przyjmując wektor liczb jako dane wejściowe.
# Elements are arranged sequentially by row.
M <- matrix(c(3:14), nrow = 4, byrow = TRUE)
print(M)
# Elements are arranged sequentially by column.
N <- matrix(c(3:14), nrow = 4, byrow = FALSE)
print(N)
# Define the column and row names.
rownames = c("row1", "row2", "row3", "row4")
colnames = c("col1", "col2", "col3")
P <- matrix(c(3:14), nrow = 4, byrow = TRUE, dimnames = list(rownames, colnames))
print(P)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[,1] [,2] [,3]
[1,] 3 4 5
[2,] 6 7 8
[3,] 9 10 11
[4,] 12 13 14
[,1] [,2] [,3]
[1,] 3 7 11
[2,] 4 8 12
[3,] 5 9 13
[4,] 6 10 14
col1 col2 col3
row1 3 4 5
row2 6 7 8
row3 9 10 11
row4 12 13 14Dostęp do elementów macierzy
Dostęp do elementów macierzy można uzyskać za pomocą indeksu kolumn i wierszy elementu. Rozważamy macierz P powyżej, aby znaleźć określone elementy poniżej.
# Define the column and row names.
rownames = c("row1", "row2", "row3", "row4")
colnames = c("col1", "col2", "col3")
# Create the matrix.
P <- matrix(c(3:14), nrow = 4, byrow = TRUE, dimnames = list(rownames, colnames))
# Access the element at 3rd column and 1st row.
print(P[1,3])
# Access the element at 2nd column and 4th row.
print(P[4,2])
# Access only the 2nd row.
print(P[2,])
# Access only the 3rd column.
print(P[,3])Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] 5
[1] 13
col1 col2 col3
6 7 8
row1 row2 row3 row4
5 8 11 14Obliczenia macierzowe
Na macierzach wykonywane są różne operacje matematyczne przy użyciu operatorów R. Wynikiem operacji jest również matryca.
Wymiary (liczba wierszy i kolumn) powinny być takie same dla macierzy biorących udział w operacji.
Dodawanie i odejmowanie macierzy
# Create two 2x3 matrices.
matrix1 <- matrix(c(3, 9, -1, 4, 2, 6), nrow = 2)
print(matrix1)
matrix2 <- matrix(c(5, 2, 0, 9, 3, 4), nrow = 2)
print(matrix2)
# Add the matrices.
result <- matrix1 + matrix2
cat("Result of addition","\n")
print(result)
# Subtract the matrices
result <- matrix1 - matrix2
cat("Result of subtraction","\n")
print(result)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[,1] [,2] [,3]
[1,] 3 -1 2
[2,] 9 4 6
[,1] [,2] [,3]
[1,] 5 0 3
[2,] 2 9 4
Result of addition
[,1] [,2] [,3]
[1,] 8 -1 5
[2,] 11 13 10
Result of subtraction
[,1] [,2] [,3]
[1,] -2 -1 -1
[2,] 7 -5 2Mnożenie i dzielenie macierzy
# Create two 2x3 matrices.
matrix1 <- matrix(c(3, 9, -1, 4, 2, 6), nrow = 2)
print(matrix1)
matrix2 <- matrix(c(5, 2, 0, 9, 3, 4), nrow = 2)
print(matrix2)
# Multiply the matrices.
result <- matrix1 * matrix2
cat("Result of multiplication","\n")
print(result)
# Divide the matrices
result <- matrix1 / matrix2
cat("Result of division","\n")
print(result)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[,1] [,2] [,3]
[1,] 3 -1 2
[2,] 9 4 6
[,1] [,2] [,3]
[1,] 5 0 3
[2,] 2 9 4
Result of multiplication
[,1] [,2] [,3]
[1,] 15 0 6
[2,] 18 36 24
Result of division
[,1] [,2] [,3]
[1,] 0.6 -Inf 0.6666667
[2,] 4.5 0.4444444 1.5000000Tablice to obiekty danych języka R, które mogą przechowywać dane w więcej niż dwóch wymiarach. Na przykład - Jeśli utworzymy tablicę wymiarów (2, 3, 4), to utworzy 4 prostokątne macierze, każda z 2 wierszami i 3 kolumnami. Tablice mogą przechowywać tylko typ danych.
Tablica jest tworzona przy użyciu array()funkcjonować. Pobiera wektory jako dane wejściowe i używa wartości wdim parametr, aby utworzyć tablicę.
Przykład
Poniższy przykład tworzy tablicę dwóch macierzy 3x3, każda z 3 wierszami i 3 kolumnami.
# Create two vectors of different lengths.
vector1 <- c(5,9,3)
vector2 <- c(10,11,12,13,14,15)
# Take these vectors as input to the array.
result <- array(c(vector1,vector2),dim = c(3,3,2))
print(result)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
, , 1
[,1] [,2] [,3]
[1,] 5 10 13
[2,] 9 11 14
[3,] 3 12 15
, , 2
[,1] [,2] [,3]
[1,] 5 10 13
[2,] 9 11 14
[3,] 3 12 15Nazewnictwo kolumn i wierszy
Możemy nadać nazwy wierszom, kolumnom i macierzom w tablicy za pomocą dimnames parametr.
# Create two vectors of different lengths.
vector1 <- c(5,9,3)
vector2 <- c(10,11,12,13,14,15)
column.names <- c("COL1","COL2","COL3")
row.names <- c("ROW1","ROW2","ROW3")
matrix.names <- c("Matrix1","Matrix2")
# Take these vectors as input to the array.
result <- array(c(vector1,vector2),dim = c(3,3,2),dimnames = list(row.names,column.names,
matrix.names))
print(result)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
, , Matrix1
COL1 COL2 COL3
ROW1 5 10 13
ROW2 9 11 14
ROW3 3 12 15
, , Matrix2
COL1 COL2 COL3
ROW1 5 10 13
ROW2 9 11 14
ROW3 3 12 15Dostęp do elementów tablicy
# Create two vectors of different lengths.
vector1 <- c(5,9,3)
vector2 <- c(10,11,12,13,14,15)
column.names <- c("COL1","COL2","COL3")
row.names <- c("ROW1","ROW2","ROW3")
matrix.names <- c("Matrix1","Matrix2")
# Take these vectors as input to the array.
result <- array(c(vector1,vector2),dim = c(3,3,2),dimnames = list(row.names,
column.names, matrix.names))
# Print the third row of the second matrix of the array.
print(result[3,,2])
# Print the element in the 1st row and 3rd column of the 1st matrix.
print(result[1,3,1])
# Print the 2nd Matrix.
print(result[,,2])Kiedy wykonujemy powyższy kod, daje on następujący wynik -
COL1 COL2 COL3
3 12 15
[1] 13
COL1 COL2 COL3
ROW1 5 10 13
ROW2 9 11 14
ROW3 3 12 15Manipulowanie elementami tablicy
Ponieważ tablica składa się z macierzy w wielu wymiarach, operacje na elementach tablicy są wykonywane przez dostęp do elementów macierzy.
# Create two vectors of different lengths.
vector1 <- c(5,9,3)
vector2 <- c(10,11,12,13,14,15)
# Take these vectors as input to the array.
array1 <- array(c(vector1,vector2),dim = c(3,3,2))
# Create two vectors of different lengths.
vector3 <- c(9,1,0)
vector4 <- c(6,0,11,3,14,1,2,6,9)
array2 <- array(c(vector1,vector2),dim = c(3,3,2))
# create matrices from these arrays.
matrix1 <- array1[,,2]
matrix2 <- array2[,,2]
# Add the matrices.
result <- matrix1+matrix2
print(result)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[,1] [,2] [,3]
[1,] 10 20 26
[2,] 18 22 28
[3,] 6 24 30Obliczenia w elementach tablicy
Możemy wykonywać obliczenia na elementach tablicy przy użyciu apply() funkcjonować.
Składnia
apply(x, margin, fun)Poniżej znajduje się opis użytych parametrów -
x jest tablicą.
margin to nazwa używanego zestawu danych.
fun to funkcja, która ma być zastosowana do elementów tablicy.
Przykład
Używamy funkcji apply () poniżej, aby obliczyć sumę elementów w wierszach tablicy we wszystkich macierzach.
# Create two vectors of different lengths.
vector1 <- c(5,9,3)
vector2 <- c(10,11,12,13,14,15)
# Take these vectors as input to the array.
new.array <- array(c(vector1,vector2),dim = c(3,3,2))
print(new.array)
# Use apply to calculate the sum of the rows across all the matrices.
result <- apply(new.array, c(1), sum)
print(result)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
, , 1
[,1] [,2] [,3]
[1,] 5 10 13
[2,] 9 11 14
[3,] 3 12 15
, , 2
[,1] [,2] [,3]
[1,] 5 10 13
[2,] 9 11 14
[3,] 3 12 15
[1] 56 68 60Czynniki to obiekty danych, które służą do kategoryzowania danych i przechowywania ich jako poziomów. Mogą przechowywać zarówno ciągi znaków, jak i liczby całkowite. Są przydatne w kolumnach, które mają ograniczoną liczbę unikalnych wartości. Takie jak „mężczyzna”, „kobieta” i „prawda, fałsz” itp. Są one przydatne w analizie danych do modelowania statystycznego.
Czynniki są tworzone przy użyciu factor () funkcji, przyjmując wektor jako dane wejściowe.
Przykład
# Create a vector as input.
data <- c("East","West","East","North","North","East","West","West","West","East","North")
print(data)
print(is.factor(data))
# Apply the factor function.
factor_data <- factor(data)
print(factor_data)
print(is.factor(factor_data))Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] "East" "West" "East" "North" "North" "East" "West" "West" "West" "East" "North"
[1] FALSE
[1] East West East North North East West West West East North
Levels: East North West
[1] TRUECzynniki w ramce danych
Tworząc dowolną ramkę danych z kolumną danych tekstowych, R traktuje kolumnę tekstową jako dane kategorialne i tworzy na niej współczynniki.
# Create the vectors for data frame.
height <- c(132,151,162,139,166,147,122)
weight <- c(48,49,66,53,67,52,40)
gender <- c("male","male","female","female","male","female","male")
# Create the data frame.
input_data <- data.frame(height,weight,gender)
print(input_data)
# Test if the gender column is a factor.
print(is.factor(input_data$gender)) # Print the gender column so see the levels. print(input_data$gender)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
height weight gender
1 132 48 male
2 151 49 male
3 162 66 female
4 139 53 female
5 166 67 male
6 147 52 female
7 122 40 male
[1] TRUE
[1] male male female female male female male
Levels: female maleZmiana kolejności poziomów
Kolejność poziomów w czynniku można zmienić, ponownie stosując funkcję współczynnika z nową kolejnością poziomów.
data <- c("East","West","East","North","North","East","West",
"West","West","East","North")
# Create the factors
factor_data <- factor(data)
print(factor_data)
# Apply the factor function with required order of the level.
new_order_data <- factor(factor_data,levels = c("East","West","North"))
print(new_order_data)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] East West East North North East West West West East North
Levels: East North West
[1] East West East North North East West West West East North
Levels: East West NorthGenerowanie poziomów czynników
Możemy generować poziomy czynników za pomocą gl()funkcjonować. Pobiera dwie liczby całkowite jako dane wejściowe, które wskazują, ile poziomów i ile razy każdy poziom.
Składnia
gl(n, k, labels)Poniżej znajduje się opis użytych parametrów -
n jest liczbą całkowitą określającą liczbę poziomów.
k jest liczbą całkowitą określającą liczbę replikacji.
labels jest wektorem etykiet dla otrzymanych poziomów czynników.
Przykład
v <- gl(3, 4, labels = c("Tampa", "Seattle","Boston"))
print(v)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
Tampa Tampa Tampa Tampa Seattle Seattle Seattle Seattle Boston
[10] Boston Boston Boston
Levels: Tampa Seattle BostonRamka danych to tabela lub dwuwymiarowa struktura przypominająca tablicę, w której każda kolumna zawiera wartości jednej zmiennej, a każdy wiersz zawiera jeden zestaw wartości z każdej kolumny.
Poniżej przedstawiono charakterystykę ramki danych.
- Nazwy kolumn nie mogą być puste.
- Nazwy wierszy powinny być unikalne.
- Dane przechowywane w ramce danych mogą mieć postać liczbową, czynnikową lub znakową.
- Każda kolumna powinna zawierać taką samą liczbę pozycji danych.
Utwórz ramkę danych
# Create the data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01", "2013-09-23", "2014-11-15", "2014-05-11",
"2015-03-27")),
stringsAsFactors = FALSE
)
# Print the data frame.
print(emp.data)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
emp_id emp_name salary start_date
1 1 Rick 623.30 2012-01-01
2 2 Dan 515.20 2013-09-23
3 3 Michelle 611.00 2014-11-15
4 4 Ryan 729.00 2014-05-11
5 5 Gary 843.25 2015-03-27Uzyskaj strukturę ramki danych
Strukturę ramki danych można zobaczyć za pomocą str() funkcjonować.
# Create the data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01", "2013-09-23", "2014-11-15", "2014-05-11",
"2015-03-27")),
stringsAsFactors = FALSE
)
# Get the structure of the data frame.
str(emp.data)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
'data.frame': 5 obs. of 4 variables:
$ emp_id : int 1 2 3 4 5 $ emp_name : chr "Rick" "Dan" "Michelle" "Ryan" ...
$ salary : num 623 515 611 729 843 $ start_date: Date, format: "2012-01-01" "2013-09-23" "2014-11-15" "2014-05-11" ...Podsumowanie danych w ramce danych
Podsumowanie statystyczne i charakter danych można uzyskać, aplikując summary() funkcjonować.
# Create the data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01", "2013-09-23", "2014-11-15", "2014-05-11",
"2015-03-27")),
stringsAsFactors = FALSE
)
# Print the summary.
print(summary(emp.data))Kiedy wykonujemy powyższy kod, daje on następujący wynik -
emp_id emp_name salary start_date
Min. :1 Length:5 Min. :515.2 Min. :2012-01-01
1st Qu.:2 Class :character 1st Qu.:611.0 1st Qu.:2013-09-23
Median :3 Mode :character Median :623.3 Median :2014-05-11
Mean :3 Mean :664.4 Mean :2014-01-14
3rd Qu.:4 3rd Qu.:729.0 3rd Qu.:2014-11-15
Max. :5 Max. :843.2 Max. :2015-03-27Wyodrębnij dane z ramki danych
Wyodrębnij określoną kolumnę z ramki danych, używając nazwy kolumny.
# Create the data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01","2013-09-23","2014-11-15","2014-05-11",
"2015-03-27")),
stringsAsFactors = FALSE
)
# Extract Specific columns.
result <- data.frame(emp.data$emp_name,emp.data$salary)
print(result)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
emp.data.emp_name emp.data.salary
1 Rick 623.30
2 Dan 515.20
3 Michelle 611.00
4 Ryan 729.00
5 Gary 843.25Wyodrębnij pierwsze dwa wiersze, a następnie wszystkie kolumny
# Create the data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01", "2013-09-23", "2014-11-15", "2014-05-11",
"2015-03-27")),
stringsAsFactors = FALSE
)
# Extract first two rows.
result <- emp.data[1:2,]
print(result)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
emp_id emp_name salary start_date
1 1 Rick 623.3 2012-01-01
2 2 Dan 515.2 2013-09-23Ekstrahować 3 rd i 5 p rzędzie z 2 -go i 4 p kolumnowej
# Create the data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01", "2013-09-23", "2014-11-15", "2014-05-11",
"2015-03-27")),
stringsAsFactors = FALSE
)
# Extract 3rd and 5th row with 2nd and 4th column.
result <- emp.data[c(3,5),c(2,4)]
print(result)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
emp_name start_date
3 Michelle 2014-11-15
5 Gary 2015-03-27Rozwiń ramkę danych
Ramkę danych można rozszerzyć, dodając kolumny i wiersze.
Dodaj kolumnę
Po prostu dodaj wektor kolumny, używając nowej nazwy kolumny.
# Create the data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01", "2013-09-23", "2014-11-15", "2014-05-11",
"2015-03-27")),
stringsAsFactors = FALSE
)
# Add the "dept" coulmn.
emp.data$dept <- c("IT","Operations","IT","HR","Finance")
v <- emp.data
print(v)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
emp_id emp_name salary start_date dept
1 1 Rick 623.30 2012-01-01 IT
2 2 Dan 515.20 2013-09-23 Operations
3 3 Michelle 611.00 2014-11-15 IT
4 4 Ryan 729.00 2014-05-11 HR
5 5 Gary 843.25 2015-03-27 FinanceDodaj wiersz
Aby trwale dodać więcej wierszy do istniejącej ramki danych, musimy wprowadzić nowe wiersze w tej samej strukturze co istniejąca ramka danych i użyć rbind() funkcjonować.
W poniższym przykładzie tworzymy ramkę danych z nowymi wierszami i łączymy ją z istniejącą ramką danych, aby utworzyć ostateczną ramkę danych.
# Create the first data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01", "2013-09-23", "2014-11-15", "2014-05-11",
"2015-03-27")),
dept = c("IT","Operations","IT","HR","Finance"),
stringsAsFactors = FALSE
)
# Create the second data frame
emp.newdata <- data.frame(
emp_id = c (6:8),
emp_name = c("Rasmi","Pranab","Tusar"),
salary = c(578.0,722.5,632.8),
start_date = as.Date(c("2013-05-21","2013-07-30","2014-06-17")),
dept = c("IT","Operations","Fianance"),
stringsAsFactors = FALSE
)
# Bind the two data frames.
emp.finaldata <- rbind(emp.data,emp.newdata)
print(emp.finaldata)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
emp_id emp_name salary start_date dept
1 1 Rick 623.30 2012-01-01 IT
2 2 Dan 515.20 2013-09-23 Operations
3 3 Michelle 611.00 2014-11-15 IT
4 4 Ryan 729.00 2014-05-11 HR
5 5 Gary 843.25 2015-03-27 Finance
6 6 Rasmi 578.00 2013-05-21 IT
7 7 Pranab 722.50 2013-07-30 Operations
8 8 Tusar 632.80 2014-06-17 FianancePakiety R to zbiór funkcji języka R, zgodny kod i przykładowe dane. Są przechowywane w katalogu o nazwie"library"w środowisku R. Domyślnie R instaluje zestaw pakietów podczas instalacji. Więcej pakietów jest dodawanych później, gdy są potrzebne do określonego celu. Kiedy uruchamiamy konsolę R, domyślnie dostępne są tylko domyślne pakiety. Inne pakiety, które są już zainstalowane, muszą zostać załadowane jawnie, aby mogły być używane przez program języka R, który ma ich używać.
Wszystkie pakiety dostępne w języku R są wymienione w Pakiety R.
Poniżej znajduje się lista poleceń używanych do sprawdzania, weryfikowania i używania pakietów R.
Sprawdź dostępne pakiety R.
Pobierz lokalizacje bibliotek zawierające pakiety języka R.
.libPaths()Kiedy wykonujemy powyższy kod, daje on następujący wynik. Może się różnić w zależności od lokalnych ustawień komputera.
[2] "C:/Program Files/R/R-3.2.2/library"Uzyskaj listę wszystkich zainstalowanych pakietów
library()Kiedy wykonujemy powyższy kod, daje on następujący wynik. Może się różnić w zależności od lokalnych ustawień komputera.
Packages in library ‘C:/Program Files/R/R-3.2.2/library’:
base The R Base Package
boot Bootstrap Functions (Originally by Angelo Canty
for S)
class Functions for Classification
cluster "Finding Groups in Data": Cluster Analysis
Extended Rousseeuw et al.
codetools Code Analysis Tools for R
compiler The R Compiler Package
datasets The R Datasets Package
foreign Read Data Stored by 'Minitab', 'S', 'SAS',
'SPSS', 'Stata', 'Systat', 'Weka', 'dBase', ...
graphics The R Graphics Package
grDevices The R Graphics Devices and Support for Colours
and Fonts
grid The Grid Graphics Package
KernSmooth Functions for Kernel Smoothing Supporting Wand
& Jones (1995)
lattice Trellis Graphics for R
MASS Support Functions and Datasets for Venables and
Ripley's MASS
Matrix Sparse and Dense Matrix Classes and Methods
methods Formal Methods and Classes
mgcv Mixed GAM Computation Vehicle with GCV/AIC/REML
Smoothness Estimation
nlme Linear and Nonlinear Mixed Effects Models
nnet Feed-Forward Neural Networks and Multinomial
Log-Linear Models
parallel Support for Parallel computation in R
rpart Recursive Partitioning and Regression Trees
spatial Functions for Kriging and Point Pattern
Analysis
splines Regression Spline Functions and Classes
stats The R Stats Package
stats4 Statistical Functions using S4 Classes
survival Survival Analysis
tcltk Tcl/Tk Interface
tools Tools for Package Development
utils The R Utils PackagePobierz wszystkie pakiety aktualnie załadowane w środowisku R.
search()Kiedy wykonujemy powyższy kod, daje on następujący wynik. Może się różnić w zależności od lokalnych ustawień komputera.
[1] ".GlobalEnv" "package:stats" "package:graphics"
[4] "package:grDevices" "package:utils" "package:datasets"
[7] "package:methods" "Autoloads" "package:base"Zainstaluj nowy pakiet
Istnieją dwa sposoby dodawania nowych pakietów R. Jeden instaluje bezpośrednio z katalogu CRAN, a drugi pobiera pakiet do lokalnego systemu i instaluje go ręcznie.
Zainstaluj bezpośrednio z CRAN
Następujące polecenie pobiera pakiety bezpośrednio ze strony internetowej CRAN i instaluje pakiet w środowisku R. Możesz zostać poproszony o wybranie najbliższego lustra. Wybierz ten odpowiedni dla swojej lokalizacji.
install.packages("Package Name")
# Install the package named "XML".
install.packages("XML")Zainstaluj pakiet ręcznie
Przejdź do łącza Pakiety R, aby pobrać wymagany pakiet. Zapisz pakiet jako plik.zip plik w odpowiednim miejscu w systemie lokalnym.
Teraz możesz uruchomić następujące polecenie, aby zainstalować ten pakiet w środowisku R.
install.packages(file_name_with_path, repos = NULL, type = "source")
# Install the package named "XML"
install.packages("E:/XML_3.98-1.3.zip", repos = NULL, type = "source")Załaduj pakiet do biblioteki
Zanim pakiet będzie można użyć w kodzie, należy go załadować do bieżącego środowiska języka R. Musisz także załadować pakiet, który był już wcześniej zainstalowany, ale nie jest dostępny w bieżącym środowisku.
Pakiet jest ładowany za pomocą następującego polecenia -
library("package Name", lib.loc = "path to library")
# Load the package named "XML"
install.packages("E:/XML_3.98-1.3.zip", repos = NULL, type = "source")Data Reshaping w R polega na zmianie sposobu organizacji danych w wiersze i kolumny. W większości przypadków przetwarzanie danych w R odbywa się poprzez przyjmowanie danych wejściowych jako ramki danych. Wyodrębnienie danych z wierszy i kolumn ramki danych jest łatwe, ale zdarzają się sytuacje, w których potrzebujemy ramki danych w formacie innym niż format, w którym ją otrzymaliśmy. R ma wiele funkcji do dzielenia, łączenia i zmiany wierszy w kolumny i odwrotnie w ramce danych.
Łączenie kolumn i wierszy w ramce danych
Możemy połączyć wiele wektorów, aby utworzyć ramkę danych za pomocą cbind()funkcjonować. Możemy również połączyć dwie ramki danych za pomocąrbind() funkcjonować.
# Create vector objects.
city <- c("Tampa","Seattle","Hartford","Denver")
state <- c("FL","WA","CT","CO")
zipcode <- c(33602,98104,06161,80294)
# Combine above three vectors into one data frame.
addresses <- cbind(city,state,zipcode)
# Print a header.
cat("# # # # The First data frame\n")
# Print the data frame.
print(addresses)
# Create another data frame with similar columns
new.address <- data.frame(
city = c("Lowry","Charlotte"),
state = c("CO","FL"),
zipcode = c("80230","33949"),
stringsAsFactors = FALSE
)
# Print a header.
cat("# # # The Second data frame\n")
# Print the data frame.
print(new.address)
# Combine rows form both the data frames.
all.addresses <- rbind(addresses,new.address)
# Print a header.
cat("# # # The combined data frame\n")
# Print the result.
print(all.addresses)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
# # # # The First data frame
city state zipcode
[1,] "Tampa" "FL" "33602"
[2,] "Seattle" "WA" "98104"
[3,] "Hartford" "CT" "6161"
[4,] "Denver" "CO" "80294"
# # # The Second data frame
city state zipcode
1 Lowry CO 80230
2 Charlotte FL 33949
# # # The combined data frame
city state zipcode
1 Tampa FL 33602
2 Seattle WA 98104
3 Hartford CT 6161
4 Denver CO 80294
5 Lowry CO 80230
6 Charlotte FL 33949Łączenie ramek danych
Możemy połączyć dwie ramki danych przy użyciu rozszerzenia merge()funkcjonować. Ramki danych muszą mieć te same nazwy kolumn, w których następuje scalanie.
W poniższym przykładzie rozważymy zbiory danych dotyczące cukrzycy u Indian Pima dostępne w bibliotekach o nazwach „MASS”. łączymy oba zbiory danych na podstawie wartości ciśnienia krwi („bp”) i wskaźnika masy ciała („bmi”). Po wybraniu tych dwóch kolumn do scalenia rekordy, w których wartości tych dwóch zmiennych są zgodne w obu zestawach danych, są łączone w jedną ramkę danych.
library(MASS)
merged.Pima <- merge(x = Pima.te, y = Pima.tr,
by.x = c("bp", "bmi"),
by.y = c("bp", "bmi")
)
print(merged.Pima)
nrow(merged.Pima)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
bp bmi npreg.x glu.x skin.x ped.x age.x type.x npreg.y glu.y skin.y ped.y
1 60 33.8 1 117 23 0.466 27 No 2 125 20 0.088
2 64 29.7 2 75 24 0.370 33 No 2 100 23 0.368
3 64 31.2 5 189 33 0.583 29 Yes 3 158 13 0.295
4 64 33.2 4 117 27 0.230 24 No 1 96 27 0.289
5 66 38.1 3 115 39 0.150 28 No 1 114 36 0.289
6 68 38.5 2 100 25 0.324 26 No 7 129 49 0.439
7 70 27.4 1 116 28 0.204 21 No 0 124 20 0.254
8 70 33.1 4 91 32 0.446 22 No 9 123 44 0.374
9 70 35.4 9 124 33 0.282 34 No 6 134 23 0.542
10 72 25.6 1 157 21 0.123 24 No 4 99 17 0.294
11 72 37.7 5 95 33 0.370 27 No 6 103 32 0.324
12 74 25.9 9 134 33 0.460 81 No 8 126 38 0.162
13 74 25.9 1 95 21 0.673 36 No 8 126 38 0.162
14 78 27.6 5 88 30 0.258 37 No 6 125 31 0.565
15 78 27.6 10 122 31 0.512 45 No 6 125 31 0.565
16 78 39.4 2 112 50 0.175 24 No 4 112 40 0.236
17 88 34.5 1 117 24 0.403 40 Yes 4 127 11 0.598
age.y type.y
1 31 No
2 21 No
3 24 No
4 21 No
5 21 No
6 43 Yes
7 36 Yes
8 40 No
9 29 Yes
10 28 No
11 55 No
12 39 No
13 39 No
14 49 Yes
15 49 Yes
16 38 No
17 28 No
[1] 17Topienie i odlewanie
Jednym z najbardziej interesujących aspektów programowania w języku R jest zmiana kształtu danych w wielu krokach w celu uzyskania pożądanego kształtu. Funkcje służące do tego są nazywanemelt() i cast().
Bierzemy pod uwagę zbiór danych o nazwie statki obecny w bibliotece o nazwie „MASA”.
library(MASS)
print(ships)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
type year period service incidents
1 A 60 60 127 0
2 A 60 75 63 0
3 A 65 60 1095 3
4 A 65 75 1095 4
5 A 70 60 1512 6
.............
.............
8 A 75 75 2244 11
9 B 60 60 44882 39
10 B 60 75 17176 29
11 B 65 60 28609 58
............
............
17 C 60 60 1179 1
18 C 60 75 552 1
19 C 65 60 781 0
............
............Roztop dane
Teraz topimy dane, aby je uporządkować, konwertując wszystkie kolumny inne niż typ i rok na wiele wierszy.
molten.ships <- melt(ships, id = c("type","year"))
print(molten.ships)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
type year variable value
1 A 60 period 60
2 A 60 period 75
3 A 65 period 60
4 A 65 period 75
............
............
9 B 60 period 60
10 B 60 period 75
11 B 65 period 60
12 B 65 period 75
13 B 70 period 60
...........
...........
41 A 60 service 127
42 A 60 service 63
43 A 65 service 1095
...........
...........
70 D 70 service 1208
71 D 75 service 0
72 D 75 service 2051
73 E 60 service 45
74 E 60 service 0
75 E 65 service 789
...........
...........
101 C 70 incidents 6
102 C 70 incidents 2
103 C 75 incidents 0
104 C 75 incidents 1
105 D 60 incidents 0
106 D 60 incidents 0
...........
...........Rzuć Molten Data
Możemy wrzucić stopione dane do nowej postaci, w której tworzona jest suma każdego typu statku dla każdego roku. Odbywa się to za pomocącast() funkcjonować.
recasted.ship <- cast(molten.ships, type+year~variable,sum)
print(recasted.ship)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
type year period service incidents
1 A 60 135 190 0
2 A 65 135 2190 7
3 A 70 135 4865 24
4 A 75 135 2244 11
5 B 60 135 62058 68
6 B 65 135 48979 111
7 B 70 135 20163 56
8 B 75 135 7117 18
9 C 60 135 1731 2
10 C 65 135 1457 1
11 C 70 135 2731 8
12 C 75 135 274 1
13 D 60 135 356 0
14 D 65 135 480 0
15 D 70 135 1557 13
16 D 75 135 2051 4
17 E 60 135 45 0
18 E 65 135 1226 14
19 E 70 135 3318 17
20 E 75 135 542 1W R możemy odczytywać dane z plików przechowywanych poza środowiskiem R. Możemy również zapisywać dane do plików, które będą przechowywane i dostępne dla systemu operacyjnego. R może czytać i zapisywać w różnych formatach plików, takich jak csv, excel, xml itp.
W tym rozdziale nauczymy się czytać dane z pliku csv, a następnie zapisywać dane do pliku csv. Plik powinien znajdować się w bieżącym katalogu roboczym, aby R. mógł go odczytać. Oczywiście możemy również ustawić własny katalog i stamtąd czytać pliki.
Pobieranie i konfigurowanie katalogu roboczego
Możesz sprawdzić, na który katalog wskazuje obszar roboczy języka R za pomocą getwd()funkcjonować. Możesz również ustawić nowy katalog roboczy za pomocąsetwd()funkcjonować.
# Get and print current working directory.
print(getwd())
# Set current working directory.
setwd("/web/com")
# Get and print current working directory.
print(getwd())Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] "/web/com/1441086124_2016"
[1] "/web/com"Wynik zależy od systemu operacyjnego i bieżącego katalogu, w którym pracujesz.
Wprowadź jako plik CSV
Plik csv to plik tekstowy, w którym wartości w kolumnach są oddzielone przecinkami. Rozważmy następujące dane obecne w pliku o nazwieinput.csv.
Możesz utworzyć ten plik za pomocą Notatnika Windows, kopiując i wklejając te dane. Zapisz plik jakoinput.csv używając opcji zapisz jako wszystkie pliki (*. *) w notatniku.
id,name,salary,start_date,dept
1,Rick,623.3,2012-01-01,IT
2,Dan,515.2,2013-09-23,Operations
3,Michelle,611,2014-11-15,IT
4,Ryan,729,2014-05-11,HR
5,Gary,843.25,2015-03-27,Finance
6,Nina,578,2013-05-21,IT
7,Simon,632.8,2013-07-30,Operations
8,Guru,722.5,2014-06-17,FinanceCzytanie pliku CSV
Poniżej znajduje się prosty przykład read.csv() funkcja odczytu pliku CSV dostępnego w twoim bieżącym katalogu roboczym -
data <- read.csv("input.csv")
print(data)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
id, name, salary, start_date, dept
1 1 Rick 623.30 2012-01-01 IT
2 2 Dan 515.20 2013-09-23 Operations
3 3 Michelle 611.00 2014-11-15 IT
4 4 Ryan 729.00 2014-05-11 HR
5 NA Gary 843.25 2015-03-27 Finance
6 6 Nina 578.00 2013-05-21 IT
7 7 Simon 632.80 2013-07-30 Operations
8 8 Guru 722.50 2014-06-17 FinanceAnaliza pliku CSV
Domyślnie read.csv()funkcja daje wynik jako ramkę danych. Można to łatwo sprawdzić w następujący sposób. Możemy również sprawdzić liczbę kolumn i wierszy.
data <- read.csv("input.csv")
print(is.data.frame(data))
print(ncol(data))
print(nrow(data))Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] TRUE
[1] 5
[1] 8Po odczytaniu danych w ramce danych możemy zastosować wszystkie funkcje mające zastosowanie do ramek danych, jak wyjaśniono w kolejnej sekcji.
Uzyskaj maksymalne wynagrodzenie
# Create a data frame.
data <- read.csv("input.csv")
# Get the max salary from data frame.
sal <- max(data$salary)
print(sal)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] 843.25Poznaj dane osoby z maksymalnym wynagrodzeniem
Możemy pobrać wiersze spełniające określone kryteria filtrowania, podobnie jak klauzula SQL where.
# Create a data frame.
data <- read.csv("input.csv")
# Get the max salary from data frame.
sal <- max(data$salary)
# Get the person detail having max salary.
retval <- subset(data, salary == max(salary))
print(retval)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
id name salary start_date dept
5 NA Gary 843.25 2015-03-27 FinanceZbierz wszystkie osoby pracujące w dziale IT
# Create a data frame.
data <- read.csv("input.csv")
retval <- subset( data, dept == "IT")
print(retval)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
id name salary start_date dept
1 1 Rick 623.3 2012-01-01 IT
3 3 Michelle 611.0 2014-11-15 IT
6 6 Nina 578.0 2013-05-21 ITPozyskaj osoby z działu IT, których pensja przekracza 600
# Create a data frame.
data <- read.csv("input.csv")
info <- subset(data, salary > 600 & dept == "IT")
print(info)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
id name salary start_date dept
1 1 Rick 623.3 2012-01-01 IT
3 3 Michelle 611.0 2014-11-15 ITZdobądź osoby, które dołączyły w 2014 roku lub później
# Create a data frame.
data <- read.csv("input.csv")
retval <- subset(data, as.Date(start_date) > as.Date("2014-01-01"))
print(retval)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
id name salary start_date dept
3 3 Michelle 611.00 2014-11-15 IT
4 4 Ryan 729.00 2014-05-11 HR
5 NA Gary 843.25 2015-03-27 Finance
8 8 Guru 722.50 2014-06-17 FinanceZapisywanie do pliku CSV
R może utworzyć plik csv z istniejącej ramki danych. Plikwrite.csv()Funkcja służy do tworzenia pliku csv. Ten plik zostanie utworzony w katalogu roboczym.
# Create a data frame.
data <- read.csv("input.csv")
retval <- subset(data, as.Date(start_date) > as.Date("2014-01-01"))
# Write filtered data into a new file.
write.csv(retval,"output.csv")
newdata <- read.csv("output.csv")
print(newdata)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
X id name salary start_date dept
1 3 3 Michelle 611.00 2014-11-15 IT
2 4 4 Ryan 729.00 2014-05-11 HR
3 5 NA Gary 843.25 2015-03-27 Finance
4 8 8 Guru 722.50 2014-06-17 FinanceTutaj kolumna X pochodzi ze zbioru danych newper. Można to usunąć, używając dodatkowych parametrów podczas zapisywania pliku.
# Create a data frame.
data <- read.csv("input.csv")
retval <- subset(data, as.Date(start_date) > as.Date("2014-01-01"))
# Write filtered data into a new file.
write.csv(retval,"output.csv", row.names = FALSE)
newdata <- read.csv("output.csv")
print(newdata)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
id name salary start_date dept
1 3 Michelle 611.00 2014-11-15 IT
2 4 Ryan 729.00 2014-05-11 HR
3 NA Gary 843.25 2015-03-27 Finance
4 8 Guru 722.50 2014-06-17 FinanceMicrosoft Excel to najczęściej używany program do obsługi arkuszy kalkulacyjnych, który przechowuje dane w formacie .xls lub .xlsx. R może czytać bezpośrednio z tych plików przy użyciu niektórych pakietów specyficznych dla programu Excel. Niewiele jest takich pakietów - XLConnect, xlsx, gdata itp. Będziemy używać pakietu xlsx. R może również zapisywać w pliku Excel przy użyciu tego pakietu.
Zainstaluj pakiet xlsx
Aby zainstalować pakiet „xlsx”, możesz użyć następującego polecenia w konsoli R. Może poprosić o zainstalowanie dodatkowych pakietów, od których zależy ten pakiet. Wykonaj to samo polecenie z wymaganą nazwą pakietu, aby zainstalować dodatkowe pakiety.
install.packages("xlsx")Sprawdź i załaduj pakiet „xlsx”
Użyj następującego polecenia, aby zweryfikować i załadować pakiet „xlsx”.
# Verify the package is installed.
any(grepl("xlsx",installed.packages()))
# Load the library into R workspace.
library("xlsx")Po uruchomieniu skryptu otrzymujemy następujące dane wyjściowe.
[1] TRUE
Loading required package: rJava
Loading required package: methods
Loading required package: xlsxjarsWprowadź jako plik xlsx
Otwórz program Microsoft Excel. Skopiuj i wklej następujące dane do arkusza roboczego o nazwie arkusz1.
id name salary start_date dept
1 Rick 623.3 1/1/2012 IT
2 Dan 515.2 9/23/2013 Operations
3 Michelle 611 11/15/2014 IT
4 Ryan 729 5/11/2014 HR
5 Gary 43.25 3/27/2015 Finance
6 Nina 578 5/21/2013 IT
7 Simon 632.8 7/30/2013 Operations
8 Guru 722.5 6/17/2014 FinanceSkopiuj i wklej również następujące dane do innego arkusza i zmień nazwę tego arkusza na „miasto”.
name city
Rick Seattle
Dan Tampa
Michelle Chicago
Ryan Seattle
Gary Houston
Nina Boston
Simon Mumbai
Guru DallasZapisz plik Excela jako „input.xlsx”. Należy go zapisać w bieżącym katalogu roboczym obszaru roboczego R.
Czytanie pliku Excel
Plik input.xlsx jest odczytywany przy użyciu rozszerzenia read.xlsx()działają, jak pokazano poniżej. Wynik jest przechowywany jako ramka danych w środowisku R.
# Read the first worksheet in the file input.xlsx.
data <- read.xlsx("input.xlsx", sheetIndex = 1)
print(data)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
id, name, salary, start_date, dept
1 1 Rick 623.30 2012-01-01 IT
2 2 Dan 515.20 2013-09-23 Operations
3 3 Michelle 611.00 2014-11-15 IT
4 4 Ryan 729.00 2014-05-11 HR
5 NA Gary 843.25 2015-03-27 Finance
6 6 Nina 578.00 2013-05-21 IT
7 7 Simon 632.80 2013-07-30 Operations
8 8 Guru 722.50 2014-06-17 FinancePlik binarny to plik, który zawiera informacje przechowywane tylko w postaci bitów i bajtów (0 i 1). Nie są one czytelne dla człowieka, ponieważ zawarte w nich bajty przekładają się na znaki i symbole, które zawierają wiele innych niedrukowalnych znaków. Próba odczytania pliku binarnego za pomocą dowolnego edytora tekstu spowoduje wyświetlenie znaków takich jak Ø i ð.
Aby plik binarny był użyteczny, musi zostać odczytany przez określone programy. Na przykład plik binarny programu Microsoft Word może zostać odczytany do postaci czytelnej dla człowieka tylko przez program Word. Co oznacza, że oprócz tekstu czytelnego dla człowieka jest o wiele więcej informacji, takich jak formatowanie znaków, numerów stron itp., Które są również przechowywane wraz ze znakami alfanumerycznymi. I wreszcie plik binarny to ciągła sekwencja bajtów. Podział wiersza, który widzimy w pliku tekstowym, to znak łączący pierwszą linię z następną.
Czasami dane generowane przez inne programy muszą zostać przetworzone przez R jako plik binarny. R jest również wymagany do tworzenia plików binarnych, które można udostępniać innym programom.
R ma dwie funkcje WriteBin() i readBin() do tworzenia i odczytywania plików binarnych.
Składnia
writeBin(object, con)
readBin(con, what, n )Poniżej znajduje się opis użytych parametrów -
con to obiekt połączenia służący do odczytu lub zapisu pliku binarnego.
object jest plikiem binarnym, który ma zostać zapisany.
what jest trybem, takim jak znak, liczba całkowita itp., reprezentującym bajty do odczytania.
n to liczba bajtów do odczytania z pliku binarnego.
Przykład
Rozważamy wbudowane w R. dane „mtcars”. Najpierw tworzymy z niego plik csv i konwertujemy go na plik binarny i przechowujemy jako plik systemu operacyjnego. Następnie czytamy ten plik binarny utworzony w R.
Pisanie pliku binarnego
Odczytujemy ramkę danych „mtcars” jako plik csv, a następnie zapisujemy ją jako plik binarny w systemie operacyjnym.
# Read the "mtcars" data frame as a csv file and store only the columns
"cyl", "am" and "gear".
write.table(mtcars, file = "mtcars.csv",row.names = FALSE, na = "",
col.names = TRUE, sep = ",")
# Store 5 records from the csv file as a new data frame.
new.mtcars <- read.table("mtcars.csv",sep = ",",header = TRUE,nrows = 5)
# Create a connection object to write the binary file using mode "wb".
write.filename = file("/web/com/binmtcars.dat", "wb")
# Write the column names of the data frame to the connection object.
writeBin(colnames(new.mtcars), write.filename)
# Write the records in each of the column to the file.
writeBin(c(new.mtcars$cyl,new.mtcars$am,new.mtcars$gear), write.filename)
# Close the file for writing so that it can be read by other program.
close(write.filename)Czytanie pliku binarnego
Utworzony powyżej plik binarny przechowuje wszystkie dane jako ciągłe bajty. Przeczytamy go więc, wybierając odpowiednie wartości nazw kolumn, a także wartości kolumn.
# Create a connection object to read the file in binary mode using "rb".
read.filename <- file("/web/com/binmtcars.dat", "rb")
# First read the column names. n = 3 as we have 3 columns.
column.names <- readBin(read.filename, character(), n = 3)
# Next read the column values. n = 18 as we have 3 column names and 15 values.
read.filename <- file("/web/com/binmtcars.dat", "rb")
bindata <- readBin(read.filename, integer(), n = 18)
# Print the data.
print(bindata)
# Read the values from 4th byte to 8th byte which represents "cyl".
cyldata = bindata[4:8]
print(cyldata)
# Read the values form 9th byte to 13th byte which represents "am".
amdata = bindata[9:13]
print(amdata)
# Read the values form 9th byte to 13th byte which represents "gear".
geardata = bindata[14:18]
print(geardata)
# Combine all the read values to a dat frame.
finaldata = cbind(cyldata, amdata, geardata)
colnames(finaldata) = column.names
print(finaldata)Kiedy wykonujemy powyższy kod, daje on następujący wynik i wykres -
[1] 7108963 1728081249 7496037 6 6 4
[7] 6 8 1 1 1 0
[13] 0 4 4 4 3 3
[1] 6 6 4 6 8
[1] 1 1 1 0 0
[1] 4 4 4 3 3
cyl am gear
[1,] 6 1 4
[2,] 6 1 4
[3,] 4 1 4
[4,] 6 0 3
[5,] 8 0 3Jak widać, odzyskaliśmy oryginalne dane, czytając plik binarny w R.
XML to format pliku, który udostępnia zarówno format pliku, jak i dane w sieci WWW, intranetach i innych miejscach przy użyciu standardowego tekstu ASCII. To skrót od Extensible Markup Language (XML). Podobnie jak HTML, zawiera znaczniki. Ale w przeciwieństwie do HTML, w którym znacznik opisuje strukturę strony, w XML znaczniki opisują znaczenie danych zawartych w pliku.
Możesz czytać plik xml w R używając pakietu "XML". Ten pakiet można zainstalować za pomocą następującego polecenia.
install.packages("XML")Dane wejściowe
Utwórz plik XMl, kopiując poniższe dane do edytora tekstu, takiego jak notatnik. Zapisz plik z rozszerzeniem.xml rozszerzenie i wybierając typ pliku jako all files(*.*).
<RECORDS>
<EMPLOYEE>
<ID>1</ID>
<NAME>Rick</NAME>
<SALARY>623.3</SALARY>
<STARTDATE>1/1/2012</STARTDATE>
<DEPT>IT</DEPT>
</EMPLOYEE>
<EMPLOYEE>
<ID>2</ID>
<NAME>Dan</NAME>
<SALARY>515.2</SALARY>
<STARTDATE>9/23/2013</STARTDATE>
<DEPT>Operations</DEPT>
</EMPLOYEE>
<EMPLOYEE>
<ID>3</ID>
<NAME>Michelle</NAME>
<SALARY>611</SALARY>
<STARTDATE>11/15/2014</STARTDATE>
<DEPT>IT</DEPT>
</EMPLOYEE>
<EMPLOYEE>
<ID>4</ID>
<NAME>Ryan</NAME>
<SALARY>729</SALARY>
<STARTDATE>5/11/2014</STARTDATE>
<DEPT>HR</DEPT>
</EMPLOYEE>
<EMPLOYEE>
<ID>5</ID>
<NAME>Gary</NAME>
<SALARY>843.25</SALARY>
<STARTDATE>3/27/2015</STARTDATE>
<DEPT>Finance</DEPT>
</EMPLOYEE>
<EMPLOYEE>
<ID>6</ID>
<NAME>Nina</NAME>
<SALARY>578</SALARY>
<STARTDATE>5/21/2013</STARTDATE>
<DEPT>IT</DEPT>
</EMPLOYEE>
<EMPLOYEE>
<ID>7</ID>
<NAME>Simon</NAME>
<SALARY>632.8</SALARY>
<STARTDATE>7/30/2013</STARTDATE>
<DEPT>Operations</DEPT>
</EMPLOYEE>
<EMPLOYEE>
<ID>8</ID>
<NAME>Guru</NAME>
<SALARY>722.5</SALARY>
<STARTDATE>6/17/2014</STARTDATE>
<DEPT>Finance</DEPT>
</EMPLOYEE>
</RECORDS>Czytanie pliku XML
R odczytuje plik xml za pomocą funkcji xmlParse(). Jest przechowywany jako lista w R.
# Load the package required to read XML files.
library("XML")
# Also load the other required package.
library("methods")
# Give the input file name to the function.
result <- xmlParse(file = "input.xml")
# Print the result.
print(result)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
1
Rick
623.3
1/1/2012
IT
2
Dan
515.2
9/23/2013
Operations
3
Michelle
611
11/15/2014
IT
4
Ryan
729
5/11/2014
HR
5
Gary
843.25
3/27/2015
Finance
6
Nina
578
5/21/2013
IT
7
Simon
632.8
7/30/2013
Operations
8
Guru
722.5
6/17/2014
FinanceUzyskaj liczbę węzłów obecnych w pliku XML
# Load the packages required to read XML files.
library("XML")
library("methods")
# Give the input file name to the function.
result <- xmlParse(file = "input.xml")
# Exract the root node form the xml file.
rootnode <- xmlRoot(result)
# Find number of nodes in the root.
rootsize <- xmlSize(rootnode)
# Print the result.
print(rootsize)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
output
[1] 8Szczegóły pierwszego węzła
Spójrzmy na pierwszy rekord przeanalizowanego pliku. To da nam wyobrażenie o różnych elementach obecnych w węźle najwyższego poziomu.
# Load the packages required to read XML files.
library("XML")
library("methods")
# Give the input file name to the function.
result <- xmlParse(file = "input.xml")
# Exract the root node form the xml file.
rootnode <- xmlRoot(result)
# Print the result.
print(rootnode[1])Kiedy wykonujemy powyższy kod, daje on następujący wynik -
$EMPLOYEE
1
Rick
623.3
1/1/2012
IT
attr(,"class")
[1] "XMLInternalNodeList" "XMLNodeList"Pobierz różne elementy węzła
# Load the packages required to read XML files.
library("XML")
library("methods")
# Give the input file name to the function.
result <- xmlParse(file = "input.xml")
# Exract the root node form the xml file.
rootnode <- xmlRoot(result)
# Get the first element of the first node.
print(rootnode[[1]][[1]])
# Get the fifth element of the first node.
print(rootnode[[1]][[5]])
# Get the second element of the third node.
print(rootnode[[3]][[2]])Kiedy wykonujemy powyższy kod, daje on następujący wynik -
1
IT
MichelleXML do ramki danych
Aby efektywnie obsługiwać dane w dużych plikach, odczytujemy dane z pliku xml jako ramkę danych. Następnie przetwórz ramkę danych do analizy danych.
# Load the packages required to read XML files.
library("XML")
library("methods")
# Convert the input xml file to a data frame.
xmldataframe <- xmlToDataFrame("input.xml")
print(xmldataframe)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
ID NAME SALARY STARTDATE DEPT
1 1 Rick 623.30 2012-01-01 IT
2 2 Dan 515.20 2013-09-23 Operations
3 3 Michelle 611.00 2014-11-15 IT
4 4 Ryan 729.00 2014-05-11 HR
5 NA Gary 843.25 2015-03-27 Finance
6 6 Nina 578.00 2013-05-21 IT
7 7 Simon 632.80 2013-07-30 Operations
8 8 Guru 722.50 2014-06-17 FinancePonieważ dane są teraz dostępne jako ramka danych, możemy użyć funkcji związanej z ramkami danych do odczytu i manipulowania plikiem.
Plik JSON przechowuje dane jako tekst w formacie czytelnym dla człowieka. Json oznacza JavaScript Object Notation. R może czytać pliki JSON przy użyciu pakietu rjson.
Zainstaluj pakiet rjson
W konsoli R możesz wydać następujące polecenie, aby zainstalować pakiet rjson.
install.packages("rjson")Dane wejściowe
Utwórz plik JSON, kopiując poniższe dane do edytora tekstu, takiego jak notatnik. Zapisz plik z rozszerzeniem.json rozszerzenie i wybierając typ pliku jako all files(*.*).
{
"ID":["1","2","3","4","5","6","7","8" ],
"Name":["Rick","Dan","Michelle","Ryan","Gary","Nina","Simon","Guru" ],
"Salary":["623.3","515.2","611","729","843.25","578","632.8","722.5" ],
"StartDate":[ "1/1/2012","9/23/2013","11/15/2014","5/11/2014","3/27/2015","5/21/2013",
"7/30/2013","6/17/2014"],
"Dept":[ "IT","Operations","IT","HR","Finance","IT","Operations","Finance"]
}Przeczytaj plik JSON
Plik JSON jest odczytywany przez R przy użyciu funkcji from JSON(). Jest przechowywany jako lista w R.
# Load the package required to read JSON files.
library("rjson")
# Give the input file name to the function.
result <- fromJSON(file = "input.json")
# Print the result.
print(result)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
$ID
[1] "1" "2" "3" "4" "5" "6" "7" "8"
$Name [1] "Rick" "Dan" "Michelle" "Ryan" "Gary" "Nina" "Simon" "Guru" $Salary
[1] "623.3" "515.2" "611" "729" "843.25" "578" "632.8" "722.5"
$StartDate [1] "1/1/2012" "9/23/2013" "11/15/2014" "5/11/2014" "3/27/2015" "5/21/2013" "7/30/2013" "6/17/2014" $Dept
[1] "IT" "Operations" "IT" "HR" "Finance" "IT"
"Operations" "Finance"Konwertuj JSON na ramkę danych
Możemy przekonwertować wyodrębnione dane powyżej na ramkę danych R w celu dalszej analizy za pomocą as.data.frame() funkcjonować.
# Load the package required to read JSON files.
library("rjson")
# Give the input file name to the function.
result <- fromJSON(file = "input.json")
# Convert JSON file to a data frame.
json_data_frame <- as.data.frame(result)
print(json_data_frame)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
id, name, salary, start_date, dept
1 1 Rick 623.30 2012-01-01 IT
2 2 Dan 515.20 2013-09-23 Operations
3 3 Michelle 611.00 2014-11-15 IT
4 4 Ryan 729.00 2014-05-11 HR
5 NA Gary 843.25 2015-03-27 Finance
6 6 Nina 578.00 2013-05-21 IT
7 7 Simon 632.80 2013-07-30 Operations
8 8 Guru 722.50 2014-06-17 FinanceWiele witryn udostępnia dane do wykorzystania przez użytkowników. Na przykład Światowa Organizacja Zdrowia (WHO) dostarcza raporty dotyczące zdrowia i informacji medycznych w postaci plików CSV, txt i XML. Korzystając z programów języka R, możemy programowo wyodrębnić określone dane z takich witryn. Niektóre pakiety w języku R, które są używane do pobierania danych z sieci, to - „RCurl”, XML ”i„ stringr ”. Są one używane do łączenia się z adresami URL, identyfikowania wymaganych łączy do plików i pobierania ich do lokalnego środowiska.
Zainstaluj pakiety R.
Następujące pakiety są wymagane do przetwarzania adresów URL i łączy do plików. Jeśli nie są dostępne w Twoim środowisku R, możesz je zainstalować za pomocą następujących poleceń.
install.packages("RCurl")
install.packages("XML")
install.packages("stringr")
install.packages("plyr")Dane wejściowe
Odwiedzimy URL danych pogodowych i pobierzemy pliki CSV za pomocą R na rok 2015.
Przykład
Użyjemy funkcji getHTMLLinks()aby zebrać adresy URL plików. Wtedy użyjemy funkcjidownload.file()aby zapisać pliki w systemie lokalnym. Ponieważ będziemy wielokrotnie stosować ten sam kod do wielu plików, utworzymy funkcję, która będzie wywoływana wiele razy. Nazwy plików są przekazywane jako parametry w postaci obiektu listy R do tej funkcji.
# Read the URL.
url <- "http://www.geos.ed.ac.uk/~weather/jcmb_ws/"
# Gather the html links present in the webpage.
links <- getHTMLLinks(url)
# Identify only the links which point to the JCMB 2015 files.
filenames <- links[str_detect(links, "JCMB_2015")]
# Store the file names as a list.
filenames_list <- as.list(filenames)
# Create a function to download the files by passing the URL and filename list.
downloadcsv <- function (mainurl,filename) {
filedetails <- str_c(mainurl,filename)
download.file(filedetails,filename)
}
# Now apply the l_ply function and save the files into the current R working directory.
l_ply(filenames,downloadcsv,mainurl = "http://www.geos.ed.ac.uk/~weather/jcmb_ws/")Sprawdź pobieranie pliku
Po uruchomieniu powyższego kodu możesz zlokalizować następujące pliki w bieżącym katalogu roboczym R.
"JCMB_2015.csv" "JCMB_2015_Apr.csv" "JCMB_2015_Feb.csv" "JCMB_2015_Jan.csv"
"JCMB_2015_Mar.csv"Dane są Relacyjne systemy baz danych są przechowywane w znormalizowanym formacie. Tak więc, aby przeprowadzić obliczenia statystyczne, będziemy potrzebować bardzo zaawansowanych i złożonych zapytań Sql. Ale R może łatwo łączyć się z wieloma relacyjnymi bazami danych, takimi jak MySql, Oracle, serwer SQL itp. I pobierać z nich rekordy jako ramkę danych. Gdy dane są dostępne w środowisku R, stają się normalnym zestawem danych R i można nimi manipulować lub analizować za pomocą wszystkich potężnych pakietów i funkcji.
W tym samouczku będziemy używać MySql jako naszej referencyjnej bazy danych do łączenia się z R.
Pakiet RMySQL
R ma wbudowany pakiet o nazwie „RMySQL”, który zapewnia natywną łączność między bazą danych MySql. Możesz zainstalować ten pakiet w środowisku R za pomocą następującego polecenia.
install.packages("RMySQL")Łączenie R z MySql
Po zainstalowaniu pakietu tworzymy obiekt połączenia w R, aby połączyć się z bazą danych. Jako dane wejściowe przyjmuje nazwę użytkownika, hasło, nazwę bazy danych i nazwę hosta.
# Create a connection Object to MySQL database.
# We will connect to the sampel database named "sakila" that comes with MySql installation.
mysqlconnection = dbConnect(MySQL(), user = 'root', password = '', dbname = 'sakila',
host = 'localhost')
# List the tables available in this database.
dbListTables(mysqlconnection)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] "actor" "actor_info"
[3] "address" "category"
[5] "city" "country"
[7] "customer" "customer_list"
[9] "film" "film_actor"
[11] "film_category" "film_list"
[13] "film_text" "inventory"
[15] "language" "nicer_but_slower_film_list"
[17] "payment" "rental"
[19] "sales_by_film_category" "sales_by_store"
[21] "staff" "staff_list"
[23] "store"Zapytania do tabel
Możemy wysyłać zapytania do tabel bazy danych w MySql za pomocą funkcji dbSendQuery(). Zapytanie jest wykonywane w MySql, a zestaw wyników jest zwracany za pomocą Rfetch()funkcjonować. Wreszcie jest przechowywany jako ramka danych w R.
# Query the "actor" tables to get all the rows.
result = dbSendQuery(mysqlconnection, "select * from actor")
# Store the result in a R data frame object. n = 5 is used to fetch first 5 rows.
data.frame = fetch(result, n = 5)
print(data.fame)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
actor_id first_name last_name last_update
1 1 PENELOPE GUINESS 2006-02-15 04:34:33
2 2 NICK WAHLBERG 2006-02-15 04:34:33
3 3 ED CHASE 2006-02-15 04:34:33
4 4 JENNIFER DAVIS 2006-02-15 04:34:33
5 5 JOHNNY LOLLOBRIGIDA 2006-02-15 04:34:33Zapytanie z klauzulą filtru
Aby otrzymać wynik, możemy przekazać dowolne prawidłowe zapytanie wybierające.
result = dbSendQuery(mysqlconnection, "select * from actor where last_name = 'TORN'")
# Fetch all the records(with n = -1) and store it as a data frame.
data.frame = fetch(result, n = -1)
print(data)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
actor_id first_name last_name last_update
1 18 DAN TORN 2006-02-15 04:34:33
2 94 KENNETH TORN 2006-02-15 04:34:33
3 102 WALTER TORN 2006-02-15 04:34:33Aktualizacja wierszy w tabelach
Możemy zaktualizować wiersze w tabeli MySQL, przekazując zapytanie aktualizujące do funkcji dbSendQuery ().
dbSendQuery(mysqlconnection, "update mtcars set disp = 168.5 where hp = 110")Po wykonaniu powyższego kodu możemy zobaczyć zaktualizowaną tabelę w środowisku MySql.
Wstawianie danych do tabel
dbSendQuery(mysqlconnection,
"insert into mtcars(row_names, mpg, cyl, disp, hp, drat, wt, qsec, vs, am, gear, carb)
values('New Mazda RX4 Wag', 21, 6, 168.5, 110, 3.9, 2.875, 17.02, 0, 1, 4, 4)"
)Po wykonaniu powyższego kodu możemy zobaczyć wiersz wstawiony do tabeli w środowisku MySql.
Tworzenie tabel w MySql
Możemy tworzyć tabele w MySql za pomocą funkcji dbWriteTable(). Zastępuje tabelę, jeśli już istnieje, i przyjmuje ramkę danych jako dane wejściowe.
# Create the connection object to the database where we want to create the table.
mysqlconnection = dbConnect(MySQL(), user = 'root', password = '', dbname = 'sakila',
host = 'localhost')
# Use the R data frame "mtcars" to create the table in MySql.
# All the rows of mtcars are taken inot MySql.
dbWriteTable(mysqlconnection, "mtcars", mtcars[, ], overwrite = TRUE)Po wykonaniu powyższego kodu możemy zobaczyć tabelę utworzoną w środowisku MySql.
Upuszczanie tabel w MySql
Możemy upuścić tabele w bazie danych MySql, przekazując instrukcję drop table do dbSendQuery () w ten sam sposób, w jaki używaliśmy go do odpytywania danych z tabel.
dbSendQuery(mysqlconnection, 'drop table if exists mtcars')Po wykonaniu powyższego kodu widzimy, że tabela została upuszczona w środowisku MySql.
Język programowania R posiada liczne biblioteki do tworzenia wykresów i wykresów. Wykres kołowy przedstawia wartości jako wycinki koła o różnych kolorach. Plasterki są oznaczone etykietami, a liczby odpowiadające każdemu wycinkowi są również przedstawione na wykresie.
W R wykres kołowy jest tworzony za pomocą pie()funkcja, która przyjmuje liczby dodatnie jako wejście wektorowe. Dodatkowe parametry służą do kontroli etykiet, koloru, tytułu itp.
Składnia
Podstawowa składnia tworzenia wykresu kołowego za pomocą R to -
pie(x, labels, radius, main, col, clockwise)Poniżej znajduje się opis użytych parametrów -
x to wektor zawierający wartości liczbowe używane na wykresie kołowym.
labels służy do opisu plastrów.
radius wskazuje promień koła na wykresie kołowym (wartość między -1 a +1).
main wskazuje tytuł wykresu.
col wskazuje paletę kolorów.
clockwise jest wartością logiczną wskazującą, czy plasterki są rysowane zgodnie z ruchem wskazówek zegara, czy przeciwnie do ruchu wskazówek zegara.
Przykład
Bardzo prosty wykres kołowy jest tworzony przy użyciu tylko wektora wejściowego i etykiet. Poniższy skrypt utworzy i zapisze wykres kołowy w bieżącym katalogu roboczym R.
# Create data for the graph.
x <- c(21, 62, 10, 53)
labels <- c("London", "New York", "Singapore", "Mumbai")
# Give the chart file a name.
png(file = "city.png")
# Plot the chart.
pie(x,labels)
# Save the file.
dev.off()Kiedy wykonujemy powyższy kod, daje on następujący wynik -
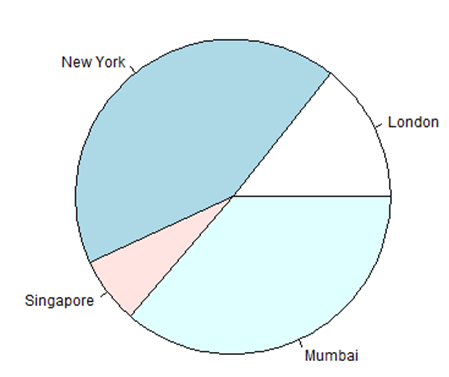
Tytuł i kolory wykresu kołowego
Możemy rozszerzyć funkcje wykresu, dodając więcej parametrów do funkcji. Użyjemy parametrumain dodać tytuł do wykresu, a kolejnym parametrem jest colktóry podczas rysowania wykresu wykorzysta tęczową paletę kolorów. Długość palety powinna być taka sama, jak liczba wartości, które mamy dla wykresu. Dlatego używamy długości (x).
Przykład
Poniższy skrypt utworzy i zapisze wykres kołowy w bieżącym katalogu roboczym R.
# Create data for the graph.
x <- c(21, 62, 10, 53)
labels <- c("London", "New York", "Singapore", "Mumbai")
# Give the chart file a name.
png(file = "city_title_colours.jpg")
# Plot the chart with title and rainbow color pallet.
pie(x, labels, main = "City pie chart", col = rainbow(length(x)))
# Save the file.
dev.off()Kiedy wykonujemy powyższy kod, daje on następujący wynik -
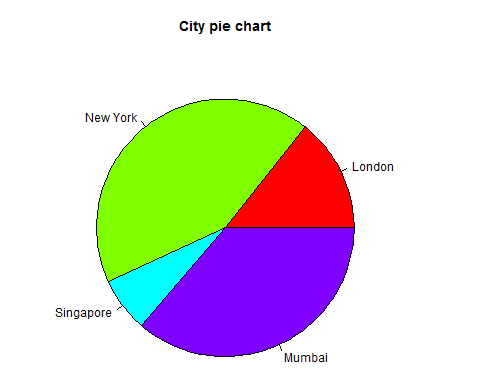
Procenty wycinków i legenda wykresu
Możemy dodać procent wycinka i legendę wykresu, tworząc dodatkowe zmienne wykresu.
# Create data for the graph.
x <- c(21, 62, 10,53)
labels <- c("London","New York","Singapore","Mumbai")
piepercent<- round(100*x/sum(x), 1)
# Give the chart file a name.
png(file = "city_percentage_legends.jpg")
# Plot the chart.
pie(x, labels = piepercent, main = "City pie chart",col = rainbow(length(x)))
legend("topright", c("London","New York","Singapore","Mumbai"), cex = 0.8,
fill = rainbow(length(x)))
# Save the file.
dev.off()Kiedy wykonujemy powyższy kod, daje on następujący wynik -
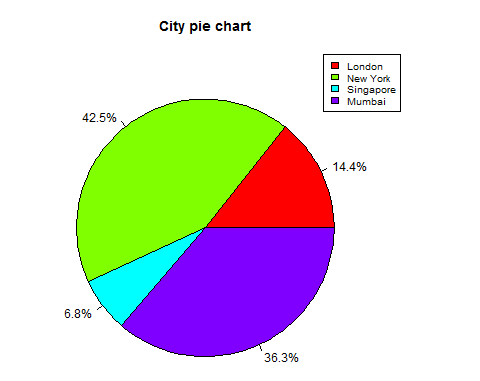
Wykres kołowy 3D
Wykres kołowy z 3 wymiarami można narysować za pomocą dodatkowych pakietów. Paczkaplotrix ma funkcję o nazwie pie3D() który jest używany do tego.
# Get the library.
library(plotrix)
# Create data for the graph.
x <- c(21, 62, 10,53)
lbl <- c("London","New York","Singapore","Mumbai")
# Give the chart file a name.
png(file = "3d_pie_chart.jpg")
# Plot the chart.
pie3D(x,labels = lbl,explode = 0.1, main = "Pie Chart of Countries ")
# Save the file.
dev.off()Kiedy wykonujemy powyższy kod, daje on następujący wynik -
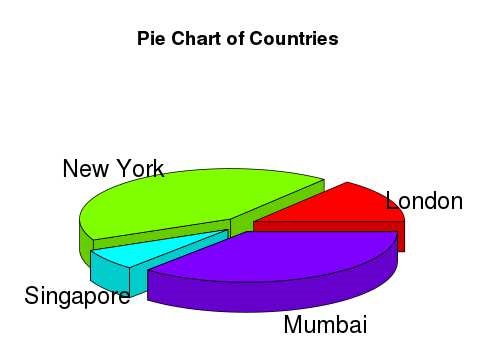
Wykres słupkowy przedstawia dane w prostokątnych słupkach o długości słupka proporcjonalnej do wartości zmiennej. R używa tej funkcjibarplot()do tworzenia wykresów słupkowych. R może rysować zarówno pionowe, jak i poziome słupki na wykresie słupkowym. Na wykresie słupkowym każdy ze słupków może mieć inny kolor.
Składnia
Podstawowa składnia tworzenia wykresu słupkowego w R to -
barplot(H,xlab,ylab,main, names.arg,col)Poniżej znajduje się opis użytych parametrów -
- H to wektor lub macierz zawierająca wartości liczbowe używane na wykresie słupkowym.
- xlab jest etykietą osi x.
- ylab jest etykietą osi y.
- main to tytuł wykresu słupkowego.
- names.arg jest wektorem nazw pojawiających się pod każdym słupkiem.
- col służy do nadawania kolorów słupkom na wykresie.
Przykład
Prosty wykres słupkowy jest tworzony przy użyciu tylko wektora wejściowego i nazwy każdego słupka.
Poniższy skrypt utworzy i zapisze wykres słupkowy w bieżącym katalogu roboczym R.
# Create the data for the chart
H <- c(7,12,28,3,41)
# Give the chart file a name
png(file = "barchart.png")
# Plot the bar chart
barplot(H)
# Save the file
dev.off()Kiedy wykonujemy powyższy kod, otrzymujemy następujący wynik -
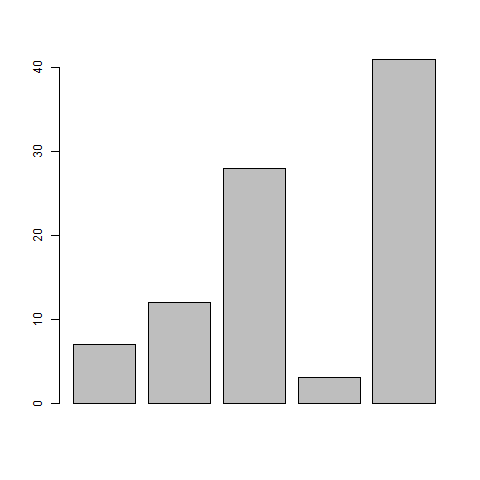
Etykiety, tytuł i kolory wykresów słupkowych
Funkcje wykresu słupkowego można rozszerzyć, dodając więcej parametrów. Plikmain parametr służy do dodawania title. Plikcolparametr służy do dodawania kolorów do słupków. Plikargs.name jest wektorem mającym taką samą liczbę wartości jak wektor wejściowy opisujący znaczenie każdego słupka.
Przykład
Poniższy skrypt utworzy i zapisze wykres słupkowy w bieżącym katalogu roboczym R.
# Create the data for the chart
H <- c(7,12,28,3,41)
M <- c("Mar","Apr","May","Jun","Jul")
# Give the chart file a name
png(file = "barchart_months_revenue.png")
# Plot the bar chart
barplot(H,names.arg=M,xlab="Month",ylab="Revenue",col="blue",
main="Revenue chart",border="red")
# Save the file
dev.off()Kiedy wykonujemy powyższy kod, otrzymujemy następujący wynik -
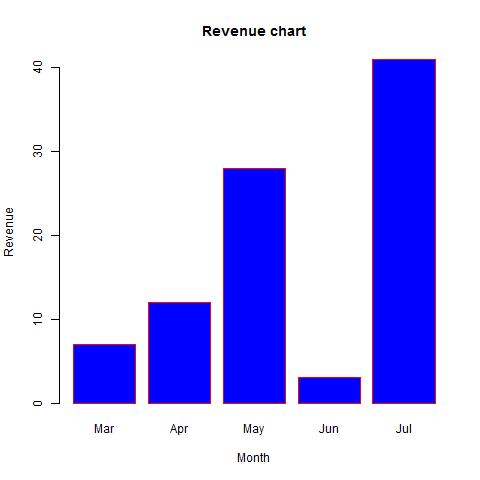
Wykres słupkowy grupowy i wykres słupkowy skumulowany
Możemy utworzyć wykres słupkowy z grupami słupków i stosów na każdym słupku, używając macierzy jako wartości wejściowych.
Więcej niż dwie zmienne są reprezentowane jako macierz, która jest używana do tworzenia grupowego wykresu słupkowego i skumulowanego wykresu słupkowego.
# Create the input vectors.
colors = c("green","orange","brown")
months <- c("Mar","Apr","May","Jun","Jul")
regions <- c("East","West","North")
# Create the matrix of the values.
Values <- matrix(c(2,9,3,11,9,4,8,7,3,12,5,2,8,10,11), nrow = 3, ncol = 5, byrow = TRUE)
# Give the chart file a name
png(file = "barchart_stacked.png")
# Create the bar chart
barplot(Values, main = "total revenue", names.arg = months, xlab = "month", ylab = "revenue", col = colors)
# Add the legend to the chart
legend("topleft", regions, cex = 1.3, fill = colors)
# Save the file
dev.off()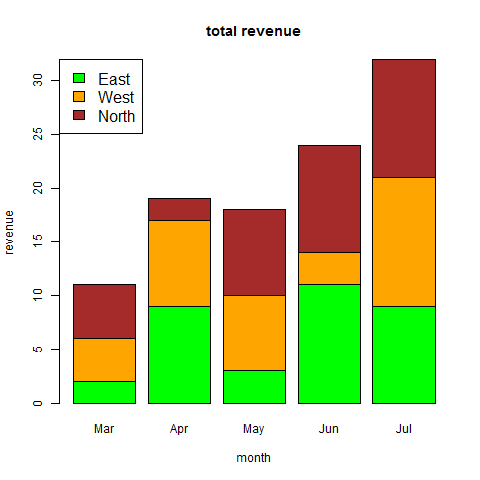
Wykresy pudełkowe są miarą tego, jak dobrze rozproszone są dane w zestawie danych. Dzieli zbiór danych na trzy kwartyle. Ten wykres przedstawia minimum, maksimum, medianę, pierwszy kwartyl i trzeci kwartyl w zbiorze danych. Jest to również przydatne do porównywania dystrybucji danych w zestawach danych poprzez rysowanie wykresów pudełkowych dla każdego z nich.
Wykresy pudełkowe są tworzone w języku R przy użyciu rozszerzenia boxplot() funkcjonować.
Składnia
Podstawowa składnia tworzenia wykresu pudełkowego w R to -
boxplot(x, data, notch, varwidth, names, main)Poniżej znajduje się opis użytych parametrów -
x jest wektorem lub formułą.
data jest ramką danych.
notchjest wartością logiczną. Ustaw jako TRUE, aby narysować wycięcie.
varwidthjest wartością logiczną. Ustaw jako prawdziwe, aby narysować szerokość prostokąta proporcjonalną do wielkości próbki.
names to etykiety grupowe, które zostaną wydrukowane pod każdym wykresem pudełkowym.
main służy do nadania tytułu wykresowi.
Przykład
Używamy zbioru danych „mtcars” dostępnego w środowisku R do tworzenia podstawowego wykresu pudełkowego. Spójrzmy na kolumny „mpg” i „cyl” w mtcars.
input <- mtcars[,c('mpg','cyl')]
print(head(input))Kiedy wykonujemy powyższy kod, otrzymujemy następujący wynik -
mpg cyl
Mazda RX4 21.0 6
Mazda RX4 Wag 21.0 6
Datsun 710 22.8 4
Hornet 4 Drive 21.4 6
Hornet Sportabout 18.7 8
Valiant 18.1 6Tworzenie wykresu pudełkowego
Poniższy skrypt utworzy wykres pudełkowy dla relacji między mpg (mile na galon) a cyl (liczbą cylindrów).
# Give the chart file a name.
png(file = "boxplot.png")
# Plot the chart.
boxplot(mpg ~ cyl, data = mtcars, xlab = "Number of Cylinders",
ylab = "Miles Per Gallon", main = "Mileage Data")
# Save the file.
dev.off()Kiedy wykonujemy powyższy kod, daje on następujący wynik -
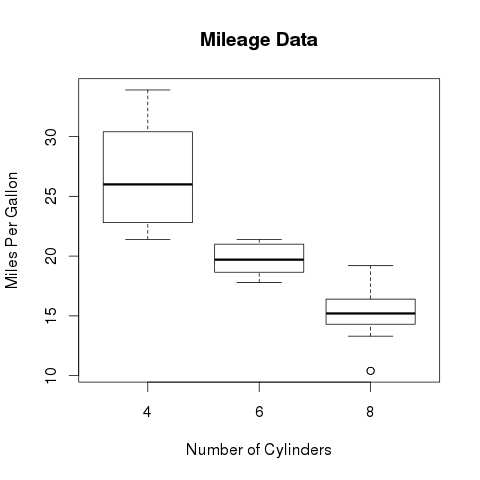
Boxplot z wycięciem
Możemy narysować wykres pudełkowy z wycięciem, aby dowiedzieć się, jak pasują do siebie mediany różnych grup danych.
Poniższy skrypt utworzy wykres pudełkowy z wycięciem dla każdej grupy danych.
# Give the chart file a name.
png(file = "boxplot_with_notch.png")
# Plot the chart.
boxplot(mpg ~ cyl, data = mtcars,
xlab = "Number of Cylinders",
ylab = "Miles Per Gallon",
main = "Mileage Data",
notch = TRUE,
varwidth = TRUE,
col = c("green","yellow","purple"),
names = c("High","Medium","Low")
)
# Save the file.
dev.off()Kiedy wykonujemy powyższy kod, daje on następujący wynik -
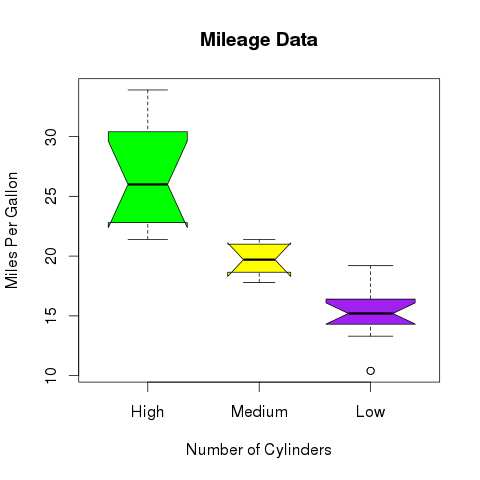
Histogram przedstawia częstości wartości zmiennej podzielonych na zakresy. Histogram jest podobny do czatu słupkowego, z tą różnicą, że grupuje wartości w ciągłe zakresy. Każdy słupek na histogramie reprezentuje wysokość liczby wartości obecnych w tym zakresie.
R tworzy histogram za pomocą hist()funkcjonować. Ta funkcja przyjmuje wektor jako dane wejściowe i wykorzystuje więcej parametrów do wykreślania histogramów.
Składnia
Podstawowa składnia tworzenia histogramu za pomocą R to -
hist(v,main,xlab,xlim,ylim,breaks,col,border)Poniżej znajduje się opis użytych parametrów -
v jest wektorem zawierającym wartości liczbowe używane w histogramie.
main wskazuje tytuł wykresu.
col służy do ustawiania koloru słupków.
border służy do ustawiania koloru obramowania każdego paska.
xlab służy do opisu osi X.
xlim służy do określenia zakresu wartości na osi X.
ylim służy do określenia zakresu wartości na osi y.
breaks jest używany do określenia szerokości każdego paska.
Przykład
Prosty histogram jest tworzony przy użyciu parametrów wektora wejściowego, etykiety, kolumny i obramowania.
Poniższy skrypt utworzy i zapisze histogram w bieżącym katalogu roboczym R.
# Create data for the graph.
v <- c(9,13,21,8,36,22,12,41,31,33,19)
# Give the chart file a name.
png(file = "histogram.png")
# Create the histogram.
hist(v,xlab = "Weight",col = "yellow",border = "blue")
# Save the file.
dev.off()Kiedy wykonujemy powyższy kod, daje on następujący wynik -
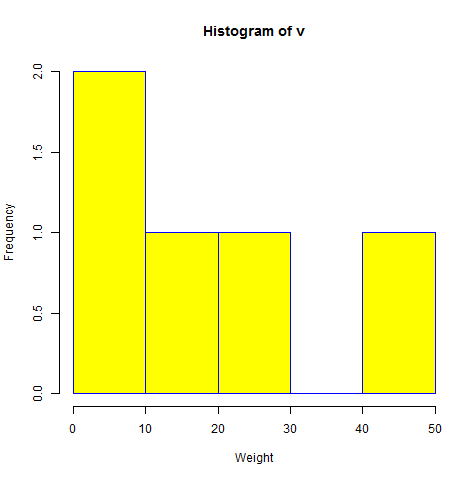
Zakres wartości X i Y.
Aby określić zakres wartości dozwolonych na osi X i osi Y, możemy użyć parametrów xlim i ylim.
Szerokość każdego paska można określić za pomocą przerw.
# Create data for the graph.
v <- c(9,13,21,8,36,22,12,41,31,33,19)
# Give the chart file a name.
png(file = "histogram_lim_breaks.png")
# Create the histogram.
hist(v,xlab = "Weight",col = "green",border = "red", xlim = c(0,40), ylim = c(0,5),
breaks = 5)
# Save the file.
dev.off()Kiedy wykonujemy powyższy kod, daje on następujący wynik -
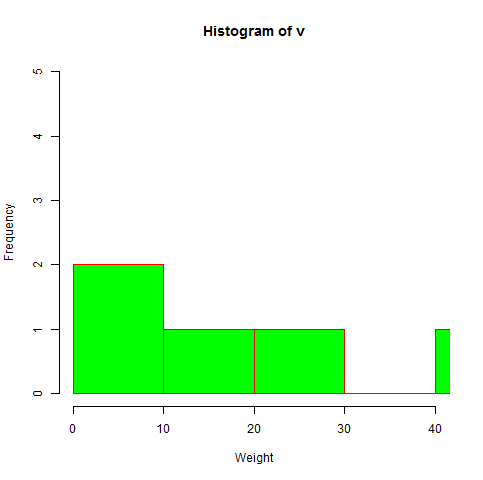
Wykres liniowy to wykres, który łączy serię punktów, rysując między nimi segmenty linii. Punkty te są uporządkowane według jednej z ich wartości współrzędnych (zwykle współrzędnej x). Wykresy liniowe są zwykle używane do identyfikowania trendów w danych.
Plik plot() funkcja w R służy do tworzenia wykresu liniowego.
Składnia
Podstawowa składnia tworzenia wykresu liniowego w R to -
plot(v,type,col,xlab,ylab)Poniżej znajduje się opis użytych parametrów -
v jest wektorem zawierającym wartości liczbowe.
type przyjmuje wartość „p”, aby narysować tylko punkty, „l”, aby narysować tylko linie, a „o”, aby narysować zarówno punkty, jak i linie.
xlab jest etykietą osi x.
ylab jest etykietą osi y.
main to tytuł wykresu.
col służy do nadawania kolorów zarówno punktom, jak i liniom.
Przykład
Prosty wykres liniowy jest tworzony przy użyciu wektora wejściowego i parametru typu „O”. Poniższy skrypt utworzy i zapisze wykres liniowy w bieżącym katalogu roboczym R.
# Create the data for the chart.
v <- c(7,12,28,3,41)
# Give the chart file a name.
png(file = "line_chart.jpg")
# Plot the bar chart.
plot(v,type = "o")
# Save the file.
dev.off()Kiedy wykonujemy powyższy kod, daje on następujący wynik -
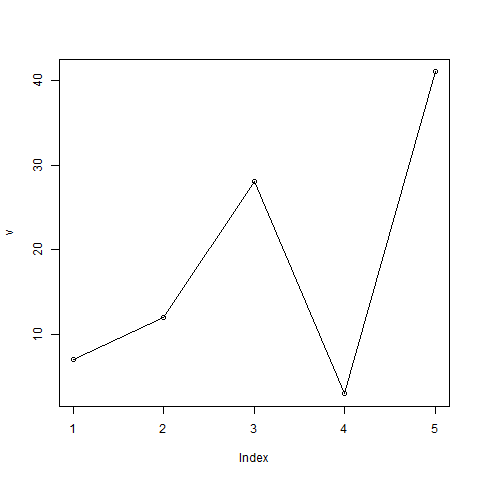
Tytuł, kolor i etykiety wykresu liniowego
Funkcje wykresu liniowego można rozszerzyć za pomocą dodatkowych parametrów. Dodajemy kolor do punktów i linii, nadajemy tytuł wykresowi oraz dodajemy etykiety do osi.
Przykład
# Create the data for the chart.
v <- c(7,12,28,3,41)
# Give the chart file a name.
png(file = "line_chart_label_colored.jpg")
# Plot the bar chart.
plot(v,type = "o", col = "red", xlab = "Month", ylab = "Rain fall",
main = "Rain fall chart")
# Save the file.
dev.off()Kiedy wykonujemy powyższy kod, daje on następujący wynik -
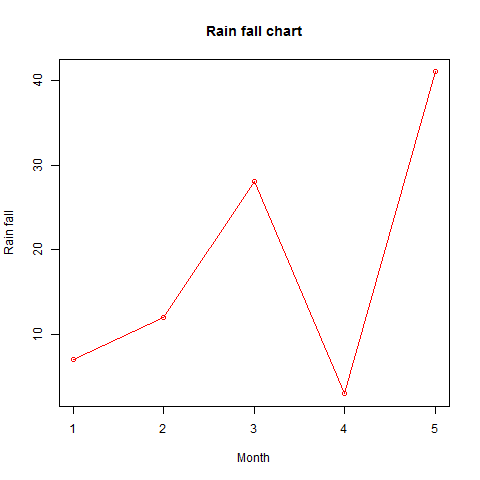
Wiele linii na wykresie liniowym
Na tym samym wykresie można narysować więcej niż jedną linię za pomocą lines()funkcjonować.
Po wykreśleniu pierwszej linii funkcja lines () może użyć dodatkowego wektora jako danych wejściowych, aby narysować drugą linię na wykresie,
# Create the data for the chart.
v <- c(7,12,28,3,41)
t <- c(14,7,6,19,3)
# Give the chart file a name.
png(file = "line_chart_2_lines.jpg")
# Plot the bar chart.
plot(v,type = "o",col = "red", xlab = "Month", ylab = "Rain fall",
main = "Rain fall chart")
lines(t, type = "o", col = "blue")
# Save the file.
dev.off()Kiedy wykonujemy powyższy kod, daje on następujący wynik -
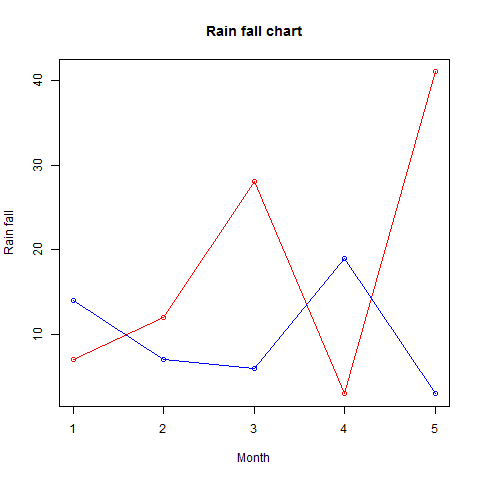
Wykresy rozrzutu pokazują wiele punktów wykreślonych na płaszczyźnie kartezjańskiej. Każdy punkt reprezentuje wartości dwóch zmiennych. Jedna zmienna jest wybierana na osi poziomej, a druga na osi pionowej.
Prosty wykres rozrzutu jest tworzony przy użyciu rozszerzenia plot() funkcjonować.
Składnia
Podstawowa składnia tworzenia wykresu rozrzutu w R to -
plot(x, y, main, xlab, ylab, xlim, ylim, axes)Poniżej znajduje się opis użytych parametrów -
x to zbiór danych, którego wartości są współrzędnymi poziomymi.
y to zbiór danych, którego wartości są współrzędnymi pionowymi.
main to kafelek wykresu.
xlab to etykieta na osi poziomej.
ylab to etykieta na osi pionowej.
xlim to granice wartości x używanych do kreślenia.
ylim to granice wartości y użytych do wykreślenia.
axes wskazuje, czy na wykresie mają być narysowane obie osie.
Przykład
Korzystamy ze zbioru danych "mtcars"dostępne w środowisku R, aby utworzyć podstawowy wykres rozrzutu. Użyjmy kolumn „wt” i „mpg” w mtcars.
input <- mtcars[,c('wt','mpg')]
print(head(input))Kiedy wykonujemy powyższy kod, daje on następujący wynik -
wt mpg
Mazda RX4 2.620 21.0
Mazda RX4 Wag 2.875 21.0
Datsun 710 2.320 22.8
Hornet 4 Drive 3.215 21.4
Hornet Sportabout 3.440 18.7
Valiant 3.460 18.1Tworzenie wykresu rozrzutu
Poniższy skrypt utworzy wykres rozrzutu dla zależności między wagą (wagą) a mpg (milami na galon).
# Get the input values.
input <- mtcars[,c('wt','mpg')]
# Give the chart file a name.
png(file = "scatterplot.png")
# Plot the chart for cars with weight between 2.5 to 5 and mileage between 15 and 30.
plot(x = input$wt,y = input$mpg,
xlab = "Weight",
ylab = "Milage",
xlim = c(2.5,5),
ylim = c(15,30),
main = "Weight vs Milage"
)
# Save the file.
dev.off()Kiedy wykonujemy powyższy kod, daje on następujący wynik -
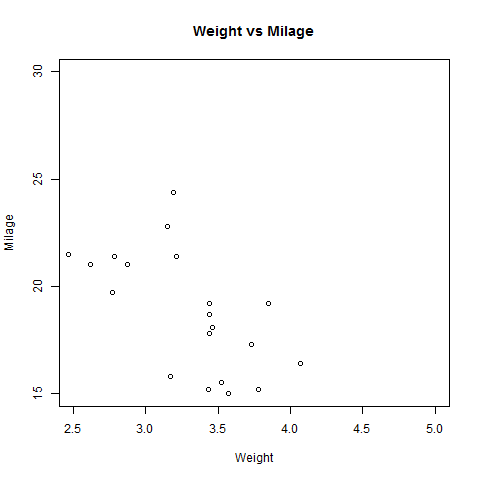
Macierze wykresu rozrzutu
Kiedy mamy więcej niż dwie zmienne i chcemy znaleźć korelację między jedną zmienną a pozostałymi, używamy macierzy wykresu rozrzutu. Używamypairs() funkcja tworzenia macierzy wykresów rozrzutu.
Składnia
Podstawowa składnia tworzenia macierzy wykresu rozrzutu w R to -
pairs(formula, data)Poniżej znajduje się opis użytych parametrów -
formula reprezentuje szereg zmiennych używanych w parach.
data reprezentuje zbiór danych, z którego zostaną pobrane zmienne.
Przykład
Każda zmienna jest powiązana z każdą z pozostałych zmiennych. Dla każdej pary wykreślany jest wykres rozrzutu.
# Give the chart file a name.
png(file = "scatterplot_matrices.png")
# Plot the matrices between 4 variables giving 12 plots.
# One variable with 3 others and total 4 variables.
pairs(~wt+mpg+disp+cyl,data = mtcars,
main = "Scatterplot Matrix")
# Save the file.
dev.off()Po wykonaniu powyższego kodu otrzymujemy następujące dane wyjściowe.
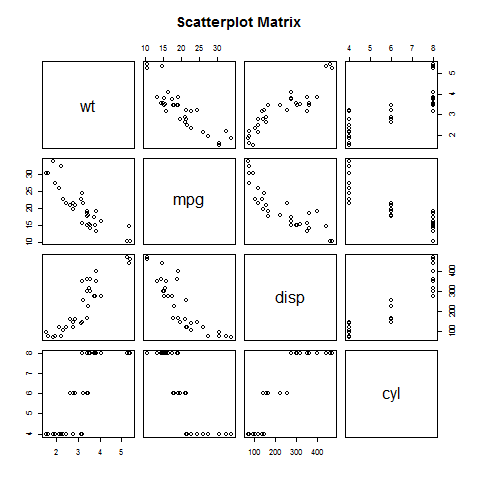
Analiza statystyczna w języku R jest wykonywana przy użyciu wielu wbudowanych funkcji. Większość z tych funkcji jest częścią pakietu podstawowego R. Te funkcje przyjmują wektor R jako dane wejściowe wraz z argumentami i podają wynik.
Funkcje, które omawiamy w tym rozdziale to średnia, mediana i mod.
Oznaczać
Oblicza się ją, biorąc sumę wartości i dzieląc ją przez liczbę wartości w serii danych.
Funkcja mean() służy do obliczenia tego w R.
Składnia
Podstawowa składnia do obliczania średniej w R to -
mean(x, trim = 0, na.rm = FALSE, ...)Poniżej znajduje się opis użytych parametrów -
x jest wektorem wejściowym.
trim służy do usuwania niektórych obserwacji z obu końców sortowanego wektora.
na.rm służy do usuwania brakujących wartości z wektora wejściowego.
Przykład
# Create a vector.
x <- c(12,7,3,4.2,18,2,54,-21,8,-5)
# Find Mean.
result.mean <- mean(x)
print(result.mean)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] 8.22Stosowanie opcji przycinania
Po podaniu parametru trymowania wartości w wektorze są sortowane, a następnie wymagana liczba obserwacji jest pomijana przy obliczaniu średniej.
Gdy trim = 0,3, 3 wartości z każdego końca zostaną usunięte z obliczeń, aby znaleźć średnią.
W tym przypadku posortowany wektor to (−21, −5, 2, 3, 4,2, 7, 8, 12, 18, 54), a wartości usunięte z wektora w celu obliczenia średniej to (−21, −5,2) od lewej i (12,18,54) od prawej.
# Create a vector.
x <- c(12,7,3,4.2,18,2,54,-21,8,-5)
# Find Mean.
result.mean <- mean(x,trim = 0.3)
print(result.mean)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] 5.55Stosowanie opcji NA
Jeśli brakuje wartości, funkcja średnia zwraca NA.
Aby usunąć brakujące wartości z obliczeń, użyj na.rm = TRUE. co oznacza usunięcie wartości NA.
# Create a vector.
x <- c(12,7,3,4.2,18,2,54,-21,8,-5,NA)
# Find mean.
result.mean <- mean(x)
print(result.mean)
# Find mean dropping NA values.
result.mean <- mean(x,na.rm = TRUE)
print(result.mean)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] NA
[1] 8.22Mediana
Najbardziej środkowa wartość w serii danych nazywana jest medianą. Plikmedian() funkcja jest używana w R do obliczenia tej wartości.
Składnia
Podstawowa składnia obliczania mediany w R to -
median(x, na.rm = FALSE)Poniżej znajduje się opis użytych parametrów -
x jest wektorem wejściowym.
na.rm służy do usuwania brakujących wartości z wektora wejściowego.
Przykład
# Create the vector.
x <- c(12,7,3,4.2,18,2,54,-21,8,-5)
# Find the median.
median.result <- median(x)
print(median.result)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] 5.6Tryb
Tryb to wartość, która ma największą liczbę wystąpień w zbiorze danych. Średnia i mediana Unike może zawierać zarówno dane liczbowe, jak i znakowe.
R nie ma standardowej wbudowanej funkcji obliczania trybu. Więc tworzymy funkcję użytkownika do obliczania trybu zbioru danych w R. Ta funkcja przyjmuje wektor jako wejście i podaje wartość trybu jako wyjście.
Przykład
# Create the function.
getmode <- function(v) {
uniqv <- unique(v)
uniqv[which.max(tabulate(match(v, uniqv)))]
}
# Create the vector with numbers.
v <- c(2,1,2,3,1,2,3,4,1,5,5,3,2,3)
# Calculate the mode using the user function.
result <- getmode(v)
print(result)
# Create the vector with characters.
charv <- c("o","it","the","it","it")
# Calculate the mode using the user function.
result <- getmode(charv)
print(result)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
[1] 2
[1] "it"Analiza regresji jest bardzo szeroko stosowanym narzędziem statystycznym do ustalenia modelu relacji między dwiema zmiennymi. Jedna z tych zmiennych nazywana jest zmienną predykcyjną, której wartość jest gromadzona w drodze eksperymentów. Druga zmienna nazywana jest zmienną odpowiedzi, której wartość pochodzi ze zmiennej predykcyjnej.
W regresji liniowej te dwie zmienne są powiązane równaniem, w którym wykładnik (potęga) obu tych zmiennych wynosi 1. Z matematycznego punktu widzenia zależność liniowa przedstawia linię prostą w postaci wykresu. Nieliniowa zależność, w której wykładnik dowolnej zmiennej nie jest równy 1, tworzy krzywą.
Ogólne równanie matematyczne dla regresji liniowej to -
y = ax + bPoniżej znajduje się opis użytych parametrów -
y jest zmienną odpowiedzi.
x jest zmienną predykcyjną.
a i b są stałymi nazywanymi współczynnikami.
Kroki prowadzące do ustalenia regresji
Prostym przykładem regresji jest przewidywanie wagi osoby, gdy znany jest jej wzrost. Aby to zrobić, musimy mieć związek między wzrostem a wagą osoby.
Kroki do stworzenia relacji to -
Przeprowadź doświadczenie polegające na zebraniu próbki obserwowanych wartości wzrostu i odpowiadającej im wagi.
Utwórz model relacji przy użyciu lm() funkcje w R.
Znajdź współczynniki z utworzonego modelu i utwórz z nich równanie matematyczne
Uzyskaj podsumowanie modelu relacji, aby poznać średni błąd w prognozowaniu. Nazywany równieżresiduals.
Aby przewidzieć wagę nowych osób, użyj predict() funkcja w R.
Dane wejściowe
Poniżej przedstawiono przykładowe dane reprezentujące obserwacje -
# Values of height
151, 174, 138, 186, 128, 136, 179, 163, 152, 131
# Values of weight.
63, 81, 56, 91, 47, 57, 76, 72, 62, 48Funkcja lm ()
Ta funkcja tworzy model relacji między predyktorem a zmienną odpowiedzi.
Składnia
Podstawowa składnia lm() funkcja w regresji liniowej to -
lm(formula,data)Poniżej znajduje się opis użytych parametrów -
formula jest symbolem przedstawiającym relację między x i y.
data jest wektorem, na którym zostanie zastosowana formuła.
Utwórz model relacji i uzyskaj współczynniki
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
# Apply the lm() function.
relation <- lm(y~x)
print(relation)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
Call:
lm(formula = y ~ x)
Coefficients:
(Intercept) x
-38.4551 0.6746Uzyskaj podsumowanie związku
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
# Apply the lm() function.
relation <- lm(y~x)
print(summary(relation))Kiedy wykonujemy powyższy kod, daje on następujący wynik -
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-6.3002 -1.6629 0.0412 1.8944 3.9775
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -38.45509 8.04901 -4.778 0.00139 **
x 0.67461 0.05191 12.997 1.16e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.253 on 8 degrees of freedom
Multiple R-squared: 0.9548, Adjusted R-squared: 0.9491
F-statistic: 168.9 on 1 and 8 DF, p-value: 1.164e-06Predict () Funkcja
Składnia
Podstawowa składnia funkcji predykcji () w regresji liniowej to -
predict(object, newdata)Poniżej znajduje się opis użytych parametrów -
object to formuła, która została już utworzona za pomocą funkcji lm ().
newdata jest wektorem zawierającym nową wartość zmiennej predykcyjnej.
Przewiduj wagę nowych osób
# The predictor vector.
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
# The resposne vector.
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
# Apply the lm() function.
relation <- lm(y~x)
# Find weight of a person with height 170.
a <- data.frame(x = 170)
result <- predict(relation,a)
print(result)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
1
76.22869Wizualizuj regresję graficznie
# Create the predictor and response variable.
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
relation <- lm(y~x)
# Give the chart file a name.
png(file = "linearregression.png")
# Plot the chart.
plot(y,x,col = "blue",main = "Height & Weight Regression",
abline(lm(x~y)),cex = 1.3,pch = 16,xlab = "Weight in Kg",ylab = "Height in cm")
# Save the file.
dev.off()Kiedy wykonujemy powyższy kod, daje on następujący wynik -
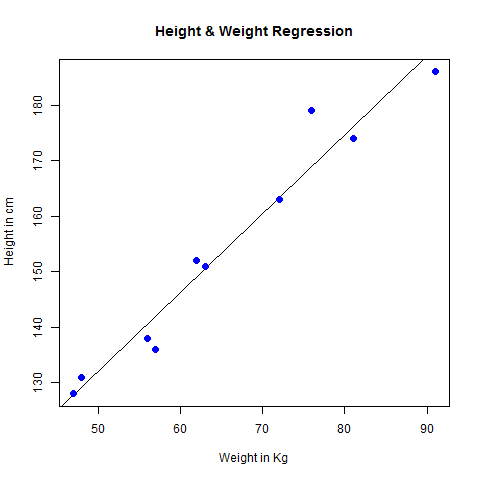
Regresja wieloraka to rozszerzenie regresji liniowej na związek między więcej niż dwoma zmiennymi. W prostej relacji liniowej mamy jeden predyktor i jedną zmienną odpowiedzi, ale w regresji wielorakiej mamy więcej niż jedną zmienną predykcyjną i jedną zmienną odpowiedzi.
Ogólne równanie matematyczne dla regresji wielorakiej to -
y = a + b1x1 + b2x2 +...bnxnPoniżej znajduje się opis użytych parametrów -
y jest zmienną odpowiedzi.
a, b1, b2...bn są współczynnikami.
x1, x2, ...xn są zmiennymi predykcyjnymi.
Tworzymy model regresji za pomocą lm()funkcja w R. Model wyznacza wartości współczynników na podstawie danych wejściowych. Następnie możemy przewidzieć wartość zmiennej odpowiedzi dla danego zestawu zmiennych predykcyjnych za pomocą tych współczynników.
Funkcja lm ()
Ta funkcja tworzy model relacji między predyktorem a zmienną odpowiedzi.
Składnia
Podstawowa składnia lm() funkcja w regresji wielorakiej to -
lm(y ~ x1+x2+x3...,data)Poniżej znajduje się opis użytych parametrów -
formula to symbol przedstawiający związek między zmienną odpowiedzi a zmiennymi predykcyjnymi.
data jest wektorem, na którym zostanie zastosowana formuła.
Przykład
Dane wejściowe
Rozważ zestaw danych „mtcars” dostępny w środowisku R. Daje porównanie różnych modeli samochodów pod względem przebiegu na galon (mpg), pojemności skokowej cylindra („disp”), mocy w koniach („hp”), masy samochodu („wt”) i kilku innych parametrów.
Celem modelu jest ustalenie związku między „mpg” jako zmienną odpowiedzi, przy czym zmienne predykcyjne to „disp”, „hp” i „wt”. W tym celu tworzymy podzbiór tych zmiennych ze zbioru danych mtcars.
input <- mtcars[,c("mpg","disp","hp","wt")]
print(head(input))Kiedy wykonujemy powyższy kod, daje on następujący wynik -
mpg disp hp wt
Mazda RX4 21.0 160 110 2.620
Mazda RX4 Wag 21.0 160 110 2.875
Datsun 710 22.8 108 93 2.320
Hornet 4 Drive 21.4 258 110 3.215
Hornet Sportabout 18.7 360 175 3.440
Valiant 18.1 225 105 3.460Utwórz model relacji i uzyskaj współczynniki
input <- mtcars[,c("mpg","disp","hp","wt")]
# Create the relationship model.
model <- lm(mpg~disp+hp+wt, data = input)
# Show the model.
print(model)
# Get the Intercept and coefficients as vector elements.
cat("# # # # The Coefficient Values # # # ","\n")
a <- coef(model)[1]
print(a)
Xdisp <- coef(model)[2]
Xhp <- coef(model)[3]
Xwt <- coef(model)[4]
print(Xdisp)
print(Xhp)
print(Xwt)Kiedy wykonujemy powyższy kod, daje on następujący wynik -
Call:
lm(formula = mpg ~ disp + hp + wt, data = input)
Coefficients:
(Intercept) disp hp wt
37.105505 -0.000937 -0.031157 -3.800891
# # # # The Coefficient Values # # #
(Intercept)
37.10551
disp
-0.0009370091
hp
-0.03115655
wt
-3.800891Utwórz równanie dla modelu regresji
Na podstawie powyższego punktu przecięcia z osią i wartości współczynników tworzymy równanie matematyczne.
Y = a+Xdisp.x1+Xhp.x2+Xwt.x3
or
Y = 37.15+(-0.000937)*x1+(-0.0311)*x2+(-3.8008)*x3Apply Equation for predicting New Values
We can use the regression equation created above to predict the mileage when a new set of values for displacement, horse power and weight is provided.
For a car with disp = 221, hp = 102 and wt = 2.91 the predicted mileage is −
Y = 37.15+(-0.000937)*221+(-0.0311)*102+(-3.8008)*2.91 = 22.7104The Logistic Regression is a regression model in which the response variable (dependent variable) has categorical values such as True/False or 0/1. It actually measures the probability of a binary response as the value of response variable based on the mathematical equation relating it with the predictor variables.
The general mathematical equation for logistic regression is −
y = 1/(1+e^-(a+b1x1+b2x2+b3x3+...))Following is the description of the parameters used −
y is the response variable.
x is the predictor variable.
a and b are the coefficients which are numeric constants.
The function used to create the regression model is the glm() function.
Syntax
The basic syntax for glm() function in logistic regression is −
glm(formula,data,family)Following is the description of the parameters used −
formula is the symbol presenting the relationship between the variables.
data is the data set giving the values of these variables.
family is R object to specify the details of the model. It's value is binomial for logistic regression.
Example
The in-built data set "mtcars" describes different models of a car with their various engine specifications. In "mtcars" data set, the transmission mode (automatic or manual) is described by the column am which is a binary value (0 or 1). We can create a logistic regression model between the columns "am" and 3 other columns - hp, wt and cyl.
# Select some columns form mtcars.
input <- mtcars[,c("am","cyl","hp","wt")]
print(head(input))When we execute the above code, it produces the following result −
am cyl hp wt
Mazda RX4 1 6 110 2.620
Mazda RX4 Wag 1 6 110 2.875
Datsun 710 1 4 93 2.320
Hornet 4 Drive 0 6 110 3.215
Hornet Sportabout 0 8 175 3.440
Valiant 0 6 105 3.460Create Regression Model
We use the glm() function to create the regression model and get its summary for analysis.
input <- mtcars[,c("am","cyl","hp","wt")]
am.data = glm(formula = am ~ cyl + hp + wt, data = input, family = binomial)
print(summary(am.data))When we execute the above code, it produces the following result −
Call:
glm(formula = am ~ cyl + hp + wt, family = binomial, data = input)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.17272 -0.14907 -0.01464 0.14116 1.27641
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 19.70288 8.11637 2.428 0.0152 *
cyl 0.48760 1.07162 0.455 0.6491
hp 0.03259 0.01886 1.728 0.0840 .
wt -9.14947 4.15332 -2.203 0.0276 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 43.2297 on 31 degrees of freedom
Residual deviance: 9.8415 on 28 degrees of freedom
AIC: 17.841
Number of Fisher Scoring iterations: 8Conclusion
In the summary as the p-value in the last column is more than 0.05 for the variables "cyl" and "hp", we consider them to be insignificant in contributing to the value of the variable "am". Only weight (wt) impacts the "am" value in this regression model.
In a random collection of data from independent sources, it is generally observed that the distribution of data is normal. Which means, on plotting a graph with the value of the variable in the horizontal axis and the count of the values in the vertical axis we get a bell shape curve. The center of the curve represents the mean of the data set. In the graph, fifty percent of values lie to the left of the mean and the other fifty percent lie to the right of the graph. This is referred as normal distribution in statistics.
R has four in built functions to generate normal distribution. They are described below.
dnorm(x, mean, sd)
pnorm(x, mean, sd)
qnorm(p, mean, sd)
rnorm(n, mean, sd)Following is the description of the parameters used in above functions −
x is a vector of numbers.
p is a vector of probabilities.
n is number of observations(sample size).
mean is the mean value of the sample data. It's default value is zero.
sd is the standard deviation. It's default value is 1.
dnorm()
This function gives height of the probability distribution at each point for a given mean and standard deviation.
# Create a sequence of numbers between -10 and 10 incrementing by 0.1.
x <- seq(-10, 10, by = .1)
# Choose the mean as 2.5 and standard deviation as 0.5.
y <- dnorm(x, mean = 2.5, sd = 0.5)
# Give the chart file a name.
png(file = "dnorm.png")
plot(x,y)
# Save the file.
dev.off()When we execute the above code, it produces the following result −
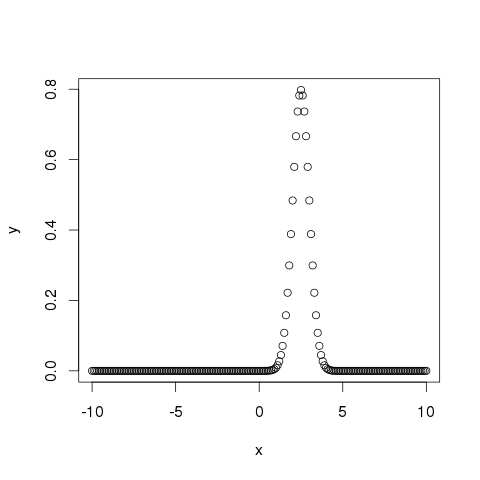
pnorm()
This function gives the probability of a normally distributed random number to be less that the value of a given number. It is also called "Cumulative Distribution Function".
# Create a sequence of numbers between -10 and 10 incrementing by 0.2.
x <- seq(-10,10,by = .2)
# Choose the mean as 2.5 and standard deviation as 2.
y <- pnorm(x, mean = 2.5, sd = 2)
# Give the chart file a name.
png(file = "pnorm.png")
# Plot the graph.
plot(x,y)
# Save the file.
dev.off()When we execute the above code, it produces the following result −
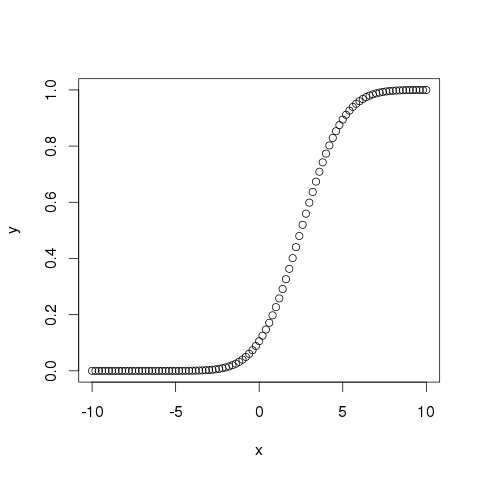
qnorm()
This function takes the probability value and gives a number whose cumulative value matches the probability value.
# Create a sequence of probability values incrementing by 0.02.
x <- seq(0, 1, by = 0.02)
# Choose the mean as 2 and standard deviation as 3.
y <- qnorm(x, mean = 2, sd = 1)
# Give the chart file a name.
png(file = "qnorm.png")
# Plot the graph.
plot(x,y)
# Save the file.
dev.off()When we execute the above code, it produces the following result −
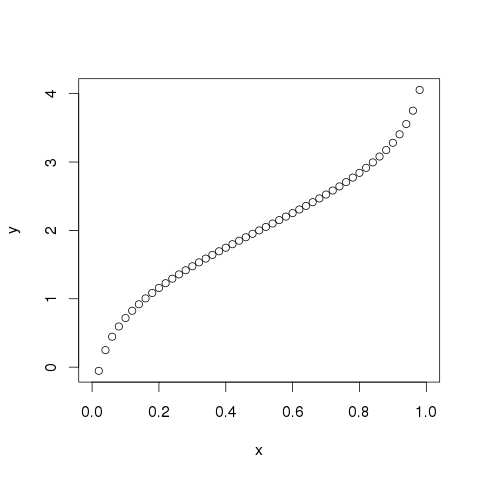
rnorm()
This function is used to generate random numbers whose distribution is normal. It takes the sample size as input and generates that many random numbers. We draw a histogram to show the distribution of the generated numbers.
# Create a sample of 50 numbers which are normally distributed.
y <- rnorm(50)
# Give the chart file a name.
png(file = "rnorm.png")
# Plot the histogram for this sample.
hist(y, main = "Normal DIstribution")
# Save the file.
dev.off()When we execute the above code, it produces the following result −
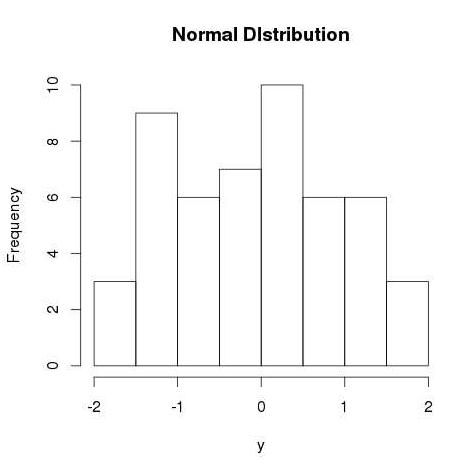
The binomial distribution model deals with finding the probability of success of an event which has only two possible outcomes in a series of experiments. For example, tossing of a coin always gives a head or a tail. The probability of finding exactly 3 heads in tossing a coin repeatedly for 10 times is estimated during the binomial distribution.
R has four in-built functions to generate binomial distribution. They are described below.
dbinom(x, size, prob)
pbinom(x, size, prob)
qbinom(p, size, prob)
rbinom(n, size, prob)Following is the description of the parameters used −
x is a vector of numbers.
p is a vector of probabilities.
n is number of observations.
size is the number of trials.
prob is the probability of success of each trial.
dbinom()
This function gives the probability density distribution at each point.
# Create a sample of 50 numbers which are incremented by 1.
x <- seq(0,50,by = 1)
# Create the binomial distribution.
y <- dbinom(x,50,0.5)
# Give the chart file a name.
png(file = "dbinom.png")
# Plot the graph for this sample.
plot(x,y)
# Save the file.
dev.off()When we execute the above code, it produces the following result −
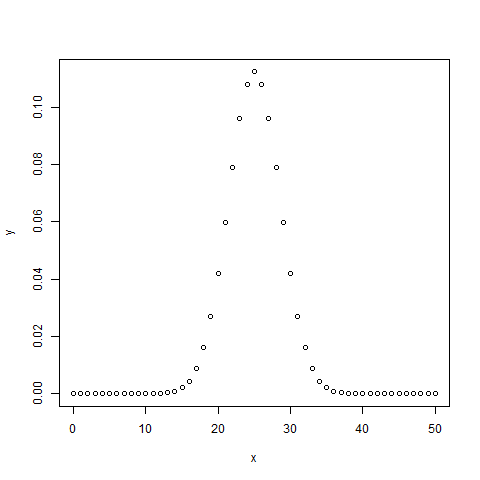
pbinom()
This function gives the cumulative probability of an event. It is a single value representing the probability.
# Probability of getting 26 or less heads from a 51 tosses of a coin.
x <- pbinom(26,51,0.5)
print(x)When we execute the above code, it produces the following result −
[1] 0.610116qbinom()
This function takes the probability value and gives a number whose cumulative value matches the probability value.
# How many heads will have a probability of 0.25 will come out when a coin
# is tossed 51 times.
x <- qbinom(0.25,51,1/2)
print(x)When we execute the above code, it produces the following result −
[1] 23rbinom()
This function generates required number of random values of given probability from a given sample.
# Find 8 random values from a sample of 150 with probability of 0.4.
x <- rbinom(8,150,.4)
print(x)When we execute the above code, it produces the following result −
[1] 58 61 59 66 55 60 61 67Poisson Regression involves regression models in which the response variable is in the form of counts and not fractional numbers. For example, the count of number of births or number of wins in a football match series. Also the values of the response variables follow a Poisson distribution.
The general mathematical equation for Poisson regression is −
log(y) = a + b1x1 + b2x2 + bnxn.....Following is the description of the parameters used −
y is the response variable.
a and b are the numeric coefficients.
x is the predictor variable.
The function used to create the Poisson regression model is the glm() function.
Syntax
The basic syntax for glm() function in Poisson regression is −
glm(formula,data,family)Following is the description of the parameters used in above functions −
formula is the symbol presenting the relationship between the variables.
data is the data set giving the values of these variables.
family is R object to specify the details of the model. It's value is 'Poisson' for Logistic Regression.
Example
We have the in-built data set "warpbreaks" which describes the effect of wool type (A or B) and tension (low, medium or high) on the number of warp breaks per loom. Let's consider "breaks" as the response variable which is a count of number of breaks. The wool "type" and "tension" are taken as predictor variables.
Input Data
input <- warpbreaks
print(head(input))When we execute the above code, it produces the following result −
breaks wool tension
1 26 A L
2 30 A L
3 54 A L
4 25 A L
5 70 A L
6 52 A LCreate Regression Model
output <-glm(formula = breaks ~ wool+tension, data = warpbreaks,
family = poisson)
print(summary(output))When we execute the above code, it produces the following result −
Call:
glm(formula = breaks ~ wool + tension, family = poisson, data = warpbreaks)
Deviance Residuals:
Min 1Q Median 3Q Max
-3.6871 -1.6503 -0.4269 1.1902 4.2616
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 3.69196 0.04541 81.302 < 2e-16 ***
woolB -0.20599 0.05157 -3.994 6.49e-05 ***
tensionM -0.32132 0.06027 -5.332 9.73e-08 ***
tensionH -0.51849 0.06396 -8.107 5.21e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 297.37 on 53 degrees of freedom
Residual deviance: 210.39 on 50 degrees of freedom
AIC: 493.06
Number of Fisher Scoring iterations: 4In the summary we look for the p-value in the last column to be less than 0.05 to consider an impact of the predictor variable on the response variable. As seen the wooltype B having tension type M and H have impact on the count of breaks.
We use Regression analysis to create models which describe the effect of variation in predictor variables on the response variable. Sometimes, if we have a categorical variable with values like Yes/No or Male/Female etc. The simple regression analysis gives multiple results for each value of the categorical variable. In such scenario, we can study the effect of the categorical variable by using it along with the predictor variable and comparing the regression lines for each level of the categorical variable. Such an analysis is termed as Analysis of Covariance also called as ANCOVA.
Example
Consider the R built in data set mtcars. In it we observer that the field "am" represents the type of transmission (auto or manual). It is a categorical variable with values 0 and 1. The miles per gallon value(mpg) of a car can also depend on it besides the value of horse power("hp").
We study the effect of the value of "am" on the regression between "mpg" and "hp". It is done by using the aov() function followed by the anova() function to compare the multiple regressions.
Input Data
Create a data frame containing the fields "mpg", "hp" and "am" from the data set mtcars. Here we take "mpg" as the response variable, "hp" as the predictor variable and "am" as the categorical variable.
input <- mtcars[,c("am","mpg","hp")]
print(head(input))When we execute the above code, it produces the following result −
am mpg hp
Mazda RX4 1 21.0 110
Mazda RX4 Wag 1 21.0 110
Datsun 710 1 22.8 93
Hornet 4 Drive 0 21.4 110
Hornet Sportabout 0 18.7 175
Valiant 0 18.1 105ANCOVA Analysis
We create a regression model taking "hp" as the predictor variable and "mpg" as the response variable taking into account the interaction between "am" and "hp".
Model with interaction between categorical variable and predictor variable
# Get the dataset.
input <- mtcars
# Create the regression model.
result <- aov(mpg~hp*am,data = input)
print(summary(result))When we execute the above code, it produces the following result −
Df Sum Sq Mean Sq F value Pr(>F)
hp 1 678.4 678.4 77.391 1.50e-09 ***
am 1 202.2 202.2 23.072 4.75e-05 ***
hp:am 1 0.0 0.0 0.001 0.981
Residuals 28 245.4 8.8
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1This result shows that both horse power and transmission type has significant effect on miles per gallon as the p value in both cases is less than 0.05. But the interaction between these two variables is not significant as the p-value is more than 0.05.
Model without interaction between categorical variable and predictor variable
# Get the dataset.
input <- mtcars
# Create the regression model.
result <- aov(mpg~hp+am,data = input)
print(summary(result))When we execute the above code, it produces the following result −
Df Sum Sq Mean Sq F value Pr(>F)
hp 1 678.4 678.4 80.15 7.63e-10 ***
am 1 202.2 202.2 23.89 3.46e-05 ***
Residuals 29 245.4 8.5
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1This result shows that both horse power and transmission type has significant effect on miles per gallon as the p value in both cases is less than 0.05.
Comparing Two Models
Now we can compare the two models to conclude if the interaction of the variables is truly in-significant. For this we use the anova() function.
# Get the dataset.
input <- mtcars
# Create the regression models.
result1 <- aov(mpg~hp*am,data = input)
result2 <- aov(mpg~hp+am,data = input)
# Compare the two models.
print(anova(result1,result2))When we execute the above code, it produces the following result −
Model 1: mpg ~ hp * am
Model 2: mpg ~ hp + am
Res.Df RSS Df Sum of Sq F Pr(>F)
1 28 245.43
2 29 245.44 -1 -0.0052515 6e-04 0.9806As the p-value is greater than 0.05 we conclude that the interaction between horse power and transmission type is not significant. So the mileage per gallon will depend in a similar manner on the horse power of the car in both auto and manual transmission mode.
Time series is a series of data points in which each data point is associated with a timestamp. A simple example is the price of a stock in the stock market at different points of time on a given day. Another example is the amount of rainfall in a region at different months of the year. R language uses many functions to create, manipulate and plot the time series data. The data for the time series is stored in an R object called time-series object. It is also a R data object like a vector or data frame.
The time series object is created by using the ts() function.
Syntax
The basic syntax for ts() function in time series analysis is −
timeseries.object.name <- ts(data, start, end, frequency)Following is the description of the parameters used −
data is a vector or matrix containing the values used in the time series.
start specifies the start time for the first observation in time series.
end specifies the end time for the last observation in time series.
frequency specifies the number of observations per unit time.
Except the parameter "data" all other parameters are optional.
Example
Consider the annual rainfall details at a place starting from January 2012. We create an R time series object for a period of 12 months and plot it.
# Get the data points in form of a R vector.
rainfall <- c(799,1174.8,865.1,1334.6,635.4,918.5,685.5,998.6,784.2,985,882.8,1071)
# Convert it to a time series object.
rainfall.timeseries <- ts(rainfall,start = c(2012,1),frequency = 12)
# Print the timeseries data.
print(rainfall.timeseries)
# Give the chart file a name.
png(file = "rainfall.png")
# Plot a graph of the time series.
plot(rainfall.timeseries)
# Save the file.
dev.off()When we execute the above code, it produces the following result and chart −
Jan Feb Mar Apr May Jun Jul Aug Sep
2012 799.0 1174.8 865.1 1334.6 635.4 918.5 685.5 998.6 784.2
Oct Nov Dec
2012 985.0 882.8 1071.0The Time series chart −
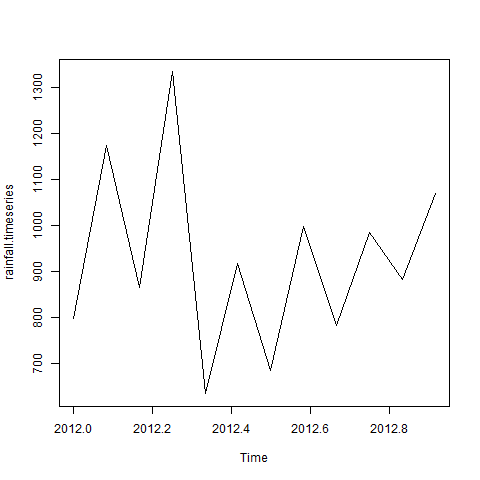
Different Time Intervals
The value of the frequency parameter in the ts() function decides the time intervals at which the data points are measured. A value of 12 indicates that the time series is for 12 months. Other values and its meaning is as below −
frequency = 12 pegs the data points for every month of a year.
frequency = 4 pegs the data points for every quarter of a year.
frequency = 6 pegs the data points for every 10 minutes of an hour.
frequency = 24*6 pegs the data points for every 10 minutes of a day.
Multiple Time Series
We can plot multiple time series in one chart by combining both the series into a matrix.
# Get the data points in form of a R vector.
rainfall1 <- c(799,1174.8,865.1,1334.6,635.4,918.5,685.5,998.6,784.2,985,882.8,1071)
rainfall2 <-
c(655,1306.9,1323.4,1172.2,562.2,824,822.4,1265.5,799.6,1105.6,1106.7,1337.8)
# Convert them to a matrix.
combined.rainfall <- matrix(c(rainfall1,rainfall2),nrow = 12)
# Convert it to a time series object.
rainfall.timeseries <- ts(combined.rainfall,start = c(2012,1),frequency = 12)
# Print the timeseries data.
print(rainfall.timeseries)
# Give the chart file a name.
png(file = "rainfall_combined.png")
# Plot a graph of the time series.
plot(rainfall.timeseries, main = "Multiple Time Series")
# Save the file.
dev.off()When we execute the above code, it produces the following result and chart −
Series 1 Series 2
Jan 2012 799.0 655.0
Feb 2012 1174.8 1306.9
Mar 2012 865.1 1323.4
Apr 2012 1334.6 1172.2
May 2012 635.4 562.2
Jun 2012 918.5 824.0
Jul 2012 685.5 822.4
Aug 2012 998.6 1265.5
Sep 2012 784.2 799.6
Oct 2012 985.0 1105.6
Nov 2012 882.8 1106.7
Dec 2012 1071.0 1337.8The Multiple Time series chart −
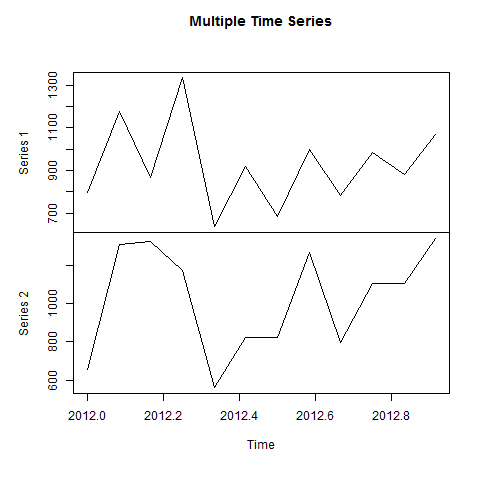
When modeling real world data for regression analysis, we observe that it is rarely the case that the equation of the model is a linear equation giving a linear graph. Most of the time, the equation of the model of real world data involves mathematical functions of higher degree like an exponent of 3 or a sin function. In such a scenario, the plot of the model gives a curve rather than a line. The goal of both linear and non-linear regression is to adjust the values of the model's parameters to find the line or curve that comes closest to your data. On finding these values we will be able to estimate the response variable with good accuracy.
In Least Square regression, we establish a regression model in which the sum of the squares of the vertical distances of different points from the regression curve is minimized. We generally start with a defined model and assume some values for the coefficients. We then apply the nls() function of R to get the more accurate values along with the confidence intervals.
Syntax
The basic syntax for creating a nonlinear least square test in R is −
nls(formula, data, start)Following is the description of the parameters used −
formula is a nonlinear model formula including variables and parameters.
data is a data frame used to evaluate the variables in the formula.
start is a named list or named numeric vector of starting estimates.
Example
We will consider a nonlinear model with assumption of initial values of its coefficients. Next we will see what is the confidence intervals of these assumed values so that we can judge how well these values fir into the model.
So let's consider the below equation for this purpose −
a = b1*x^2+b2Let's assume the initial coefficients to be 1 and 3 and fit these values into nls() function.
xvalues <- c(1.6,2.1,2,2.23,3.71,3.25,3.4,3.86,1.19,2.21)
yvalues <- c(5.19,7.43,6.94,8.11,18.75,14.88,16.06,19.12,3.21,7.58)
# Give the chart file a name.
png(file = "nls.png")
# Plot these values.
plot(xvalues,yvalues)
# Take the assumed values and fit into the model.
model <- nls(yvalues ~ b1*xvalues^2+b2,start = list(b1 = 1,b2 = 3))
# Plot the chart with new data by fitting it to a prediction from 100 data points.
new.data <- data.frame(xvalues = seq(min(xvalues),max(xvalues),len = 100))
lines(new.data$xvalues,predict(model,newdata = new.data))
# Save the file.
dev.off()
# Get the sum of the squared residuals.
print(sum(resid(model)^2))
# Get the confidence intervals on the chosen values of the coefficients.
print(confint(model))When we execute the above code, it produces the following result −
[1] 1.081935
Waiting for profiling to be done...
2.5% 97.5%
b1 1.137708 1.253135
b2 1.497364 2.496484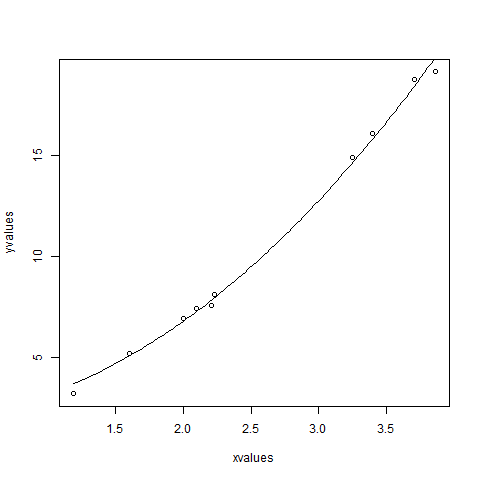
We can conclude that the value of b1 is more close to 1 while the value of b2 is more close to 2 and not 3.
Decision tree is a graph to represent choices and their results in form of a tree. The nodes in the graph represent an event or choice and the edges of the graph represent the decision rules or conditions. It is mostly used in Machine Learning and Data Mining applications using R.
Examples of use of decision tress is − predicting an email as spam or not spam, predicting of a tumor is cancerous or predicting a loan as a good or bad credit risk based on the factors in each of these. Generally, a model is created with observed data also called training data. Then a set of validation data is used to verify and improve the model. R has packages which are used to create and visualize decision trees. For new set of predictor variable, we use this model to arrive at a decision on the category (yes/No, spam/not spam) of the data.
The R package "party" is used to create decision trees.
Install R Package
Use the below command in R console to install the package. You also have to install the dependent packages if any.
install.packages("party")The package "party" has the function ctree() which is used to create and analyze decison tree.
Syntax
The basic syntax for creating a decision tree in R is −
ctree(formula, data)Following is the description of the parameters used −
formula is a formula describing the predictor and response variables.
data is the name of the data set used.
Input Data
We will use the R in-built data set named readingSkills to create a decision tree. It describes the score of someone's readingSkills if we know the variables "age","shoesize","score" and whether the person is a native speaker or not.
Here is the sample data.
# Load the party package. It will automatically load other
# dependent packages.
library(party)
# Print some records from data set readingSkills.
print(head(readingSkills))When we execute the above code, it produces the following result and chart −
nativeSpeaker age shoeSize score
1 yes 5 24.83189 32.29385
2 yes 6 25.95238 36.63105
3 no 11 30.42170 49.60593
4 yes 7 28.66450 40.28456
5 yes 11 31.88207 55.46085
6 yes 10 30.07843 52.83124
Loading required package: methods
Loading required package: grid
...............................
...............................Example
We will use the ctree() function to create the decision tree and see its graph.
# Load the party package. It will automatically load other
# dependent packages.
library(party)
# Create the input data frame.
input.dat <- readingSkills[c(1:105),]
# Give the chart file a name.
png(file = "decision_tree.png")
# Create the tree.
output.tree <- ctree(
nativeSpeaker ~ age + shoeSize + score,
data = input.dat)
# Plot the tree.
plot(output.tree)
# Save the file.
dev.off()Kiedy wykonujemy powyższy kod, daje on następujący wynik -
null device
1
Loading required package: methods
Loading required package: grid
Loading required package: mvtnorm
Loading required package: modeltools
Loading required package: stats4
Loading required package: strucchange
Loading required package: zoo
Attaching package: ‘zoo’
The following objects are masked from ‘package:base’:
as.Date, as.Date.numeric
Loading required package: sandwich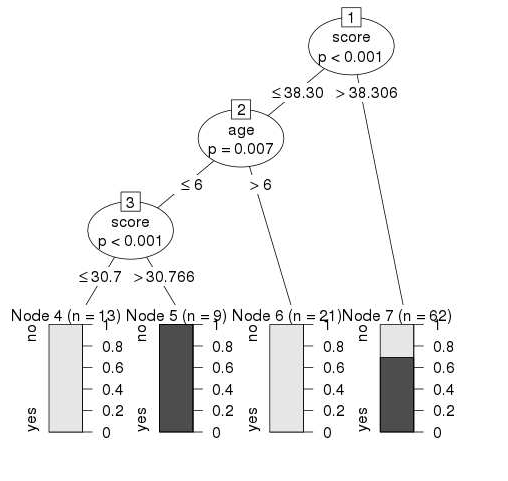
Wniosek
Z przedstawionego powyżej drzewa decyzyjnego możemy wywnioskować, że każdy, kto ma wynik umiejętności czytania poniżej 38,3 i wiek powyżej 6 lat, nie jest native speakerem.
W podejściu lasu losowego tworzona jest duża liczba drzew decyzyjnych. Każda obserwacja jest wprowadzana do każdego drzewa decyzyjnego. Najpowszechniejszy wynik każdej obserwacji jest używany jako wynik końcowy. Nowa obserwacja jest wprowadzana do wszystkich drzew i uzyskuje większość głosów dla każdego modelu klasyfikacji.
Oszacowano błąd dla przypadków, które nie zostały wykorzystane podczas budowania drzewa. To się nazywaOOB (Out-of-bag) oszacowanie błędu, które podaje się w procentach.
Pakiet R. "randomForest" służy do tworzenia losowych lasów.
Zainstaluj pakiet R.
Użyj poniższego polecenia w konsoli R, aby zainstalować pakiet. Musisz także zainstalować pakiety zależne, jeśli takie istnieją.
install.packages("randomForest)Pakiet „randomForest” ma funkcję randomForest() który służy do tworzenia i analizowania losowych lasów.
Składnia
Podstawowa składnia tworzenia losowego lasu w R to -
randomForest(formula, data)Poniżej znajduje się opis użytych parametrów -
formula to wzór opisujący predyktor i zmienne odpowiedzi.
data to nazwa używanego zestawu danych.
Dane wejściowe
Do stworzenia drzewa decyzyjnego użyjemy wbudowanego zestawu danych języka R o nazwie readingSkills. Opisuje wynik czyjegoś czytania Umiejętności, jeśli znamy zmienne „wiek”, „rozmiar buta”, „wynik” i czy dana osoba jest native speakerem.
Oto przykładowe dane.
# Load the party package. It will automatically load other
# required packages.
library(party)
# Print some records from data set readingSkills.
print(head(readingSkills))Kiedy wykonujemy powyższy kod, daje on następujący wynik i wykres -
nativeSpeaker age shoeSize score
1 yes 5 24.83189 32.29385
2 yes 6 25.95238 36.63105
3 no 11 30.42170 49.60593
4 yes 7 28.66450 40.28456
5 yes 11 31.88207 55.46085
6 yes 10 30.07843 52.83124
Loading required package: methods
Loading required package: grid
...............................
...............................Przykład
Będziemy używać randomForest() funkcję, aby utworzyć drzewo decyzyjne i zobaczyć jego wykres.
# Load the party package. It will automatically load other
# required packages.
library(party)
library(randomForest)
# Create the forest.
output.forest <- randomForest(nativeSpeaker ~ age + shoeSize + score,
data = readingSkills)
# View the forest results.
print(output.forest)
# Importance of each predictor.
print(importance(fit,type = 2))Kiedy wykonujemy powyższy kod, daje on następujący wynik -
Call:
randomForest(formula = nativeSpeaker ~ age + shoeSize + score,
data = readingSkills)
Type of random forest: classification
Number of trees: 500
No. of variables tried at each split: 1
OOB estimate of error rate: 1%
Confusion matrix:
no yes class.error
no 99 1 0.01
yes 1 99 0.01
MeanDecreaseGini
age 13.95406
shoeSize 18.91006
score 56.73051Wniosek
Z przedstawionego powyżej losowego lasu możemy wywnioskować, że rozmiar buta i punktacja są ważnymi czynnikami decydującymi o tym, czy ktoś jest native speakerem, czy nie. Również model ma tylko 1% błąd, co oznacza, że możemy przewidywać z 99% dokładnością.
Analiza przeżycia zajmuje się przewidywaniem czasu, w którym nastąpi określone wydarzenie. Jest również znany jako analiza czasu awarii lub analiza czasu do śmierci. Na przykład przewidywanie liczby dni, w których osoba z rakiem przeżyje lub przewidywanie czasu, w którym system mechaniczny ulegnie awarii.
Pakiet R. o nazwie survivalsłuży do przeprowadzania analizy przeżycia. Ten pakiet zawiera funkcjęSurv()który przyjmuje dane wejściowe jako formułę R i tworzy obiekt przetrwania wśród wybranych zmiennych do analizy. Następnie używamy funkcjisurvfit() aby stworzyć wykres do analizy.
Zainstaluj pakiet
install.packages("survival")Składnia
Podstawowa składnia tworzenia analizy przetrwania w R to -
Surv(time,event)
survfit(formula)Poniżej znajduje się opis użytych parametrów -
time to czas do wystąpienia zdarzenia.
event wskazuje stan wystąpienia spodziewanego zdarzenia.
formula to związek między zmiennymi predykcyjnymi.
Przykład
Rozważymy zestaw danych o nazwie „pbc” obecny w pakietach przetrwania zainstalowanych powyżej. Opisuje dane dotyczące przeżycia osób dotkniętych pierwotną marskością żółciową wątroby (PBC) wątroby. Wśród wielu kolumn obecnych w zbiorze danych zajmujemy się przede wszystkim polami „czas” i „stan”. Czas reprezentuje liczbę dni między rejestracją pacjenta a wcześniejszym wydarzeniem między otrzymaniem przez pacjenta przeszczepu wątroby lub śmiercią pacjenta.
# Load the library.
library("survival")
# Print first few rows.
print(head(pbc))Kiedy wykonujemy powyższy kod, daje on następujący wynik i wykres -
id time status trt age sex ascites hepato spiders edema bili chol
1 1 400 2 1 58.76523 f 1 1 1 1.0 14.5 261
2 2 4500 0 1 56.44627 f 0 1 1 0.0 1.1 302
3 3 1012 2 1 70.07255 m 0 0 0 0.5 1.4 176
4 4 1925 2 1 54.74059 f 0 1 1 0.5 1.8 244
5 5 1504 1 2 38.10541 f 0 1 1 0.0 3.4 279
6 6 2503 2 2 66.25873 f 0 1 0 0.0 0.8 248
albumin copper alk.phos ast trig platelet protime stage
1 2.60 156 1718.0 137.95 172 190 12.2 4
2 4.14 54 7394.8 113.52 88 221 10.6 3
3 3.48 210 516.0 96.10 55 151 12.0 4
4 2.54 64 6121.8 60.63 92 183 10.3 4
5 3.53 143 671.0 113.15 72 136 10.9 3
6 3.98 50 944.0 93.00 63 NA 11.0 3Na podstawie powyższych danych rozważamy czas i status naszej analizy.
Stosowanie funkcji Surv () i Survfit ()
Teraz przystępujemy do stosowania Surv() funkcji do powyższego zestawu danych i utwórz wykres, który pokaże trend.
# Load the library.
library("survival")
# Create the survival object.
survfit(Surv(pbc$time,pbc$status == 2)~1) # Give the chart file a name. png(file = "survival.png") # Plot the graph. plot(survfit(Surv(pbc$time,pbc$status == 2)~1))
# Save the file.
dev.off()Kiedy wykonujemy powyższy kod, daje on następujący wynik i wykres -
Call: survfit(formula = Surv(pbc$time, pbc$status == 2) ~ 1)
n events median 0.95LCL 0.95UCL
418 161 3395 3090 3853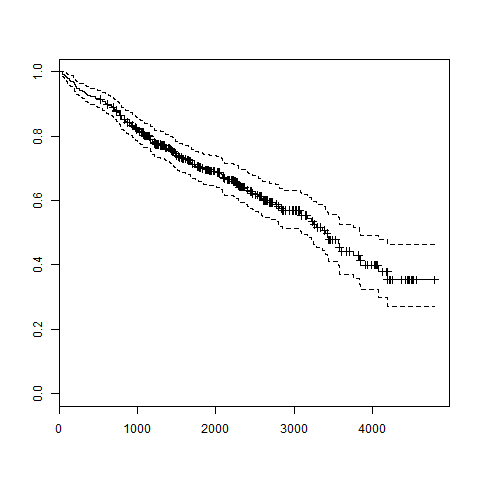
Tendencja na powyższym wykresie pomaga nam przewidzieć prawdopodobieństwo przeżycia pod koniec określonej liczby dni.
Chi-Square testto metoda statystyczna pozwalająca określić, czy dwie zmienne kategorialne mają między sobą istotną korelację. Obie te zmienne powinny pochodzić z tej samej populacji i powinny być kategoryczne, takie jak - Tak / Nie, Mężczyzna / Kobieta, Czerwony / Zielony itp.
Na przykład możemy zbudować zbiór danych z obserwacjami wzorców kupowania lodów przez ludzi i spróbować skorelować płeć osoby ze smakiem lodów, które preferują. Jeśli zostanie znaleziona korelacja, możemy zaplanować odpowiedni zapas smaków, znając liczbę osób odwiedzających.
Składnia
Funkcja używana do wykonywania testu chi-kwadrat to chisq.test().
Podstawowa składnia tworzenia testu chi-kwadrat w języku R to -
chisq.test(data)Poniżej znajduje się opis użytych parametrów -
data to dane w postaci tabeli zawierającej zliczanie wartości zmiennych w obserwacji.
Przykład
Dane dotyczące Cars93 zostaną umieszczone w bibliotece „MASS”, która przedstawia sprzedaż różnych modeli samochodów w roku 1993.
library("MASS")
print(str(Cars93))Kiedy wykonujemy powyższy kod, daje on następujący wynik -
'data.frame': 93 obs. of 27 variables:
$ Manufacturer : Factor w/ 32 levels "Acura","Audi",..: 1 1 2 2 3 4 4 4 4 5 ...
$ Model : Factor w/ 93 levels "100","190E","240",..: 49 56 9 1 6 24 54 74 73 35 ... $ Type : Factor w/ 6 levels "Compact","Large",..: 4 3 1 3 3 3 2 2 3 2 ...
$ Min.Price : num 12.9 29.2 25.9 30.8 23.7 14.2 19.9 22.6 26.3 33 ... $ Price : num 15.9 33.9 29.1 37.7 30 15.7 20.8 23.7 26.3 34.7 ...
$ Max.Price : num 18.8 38.7 32.3 44.6 36.2 17.3 21.7 24.9 26.3 36.3 ... $ MPG.city : int 25 18 20 19 22 22 19 16 19 16 ...
$ MPG.highway : int 31 25 26 26 30 31 28 25 27 25 ... $ AirBags : Factor w/ 3 levels "Driver & Passenger",..: 3 1 2 1 2 2 2 2 2 2 ...
$ DriveTrain : Factor w/ 3 levels "4WD","Front",..: 2 2 2 2 3 2 2 3 2 2 ... $ Cylinders : Factor w/ 6 levels "3","4","5","6",..: 2 4 4 4 2 2 4 4 4 5 ...
$ EngineSize : num 1.8 3.2 2.8 2.8 3.5 2.2 3.8 5.7 3.8 4.9 ... $ Horsepower : int 140 200 172 172 208 110 170 180 170 200 ...
$ RPM : int 6300 5500 5500 5500 5700 5200 4800 4000 4800 4100 ... $ Rev.per.mile : int 2890 2335 2280 2535 2545 2565 1570 1320 1690 1510 ...
$ Man.trans.avail : Factor w/ 2 levels "No","Yes": 2 2 2 2 2 1 1 1 1 1 ... $ Fuel.tank.capacity: num 13.2 18 16.9 21.1 21.1 16.4 18 23 18.8 18 ...
$ Passengers : int 5 5 5 6 4 6 6 6 5 6 ... $ Length : int 177 195 180 193 186 189 200 216 198 206 ...
$ Wheelbase : int 102 115 102 106 109 105 111 116 108 114 ... $ Width : int 68 71 67 70 69 69 74 78 73 73 ...
$ Turn.circle : int 37 38 37 37 39 41 42 45 41 43 ... $ Rear.seat.room : num 26.5 30 28 31 27 28 30.5 30.5 26.5 35 ...
$ Luggage.room : int 11 15 14 17 13 16 17 21 14 18 ... $ Weight : int 2705 3560 3375 3405 3640 2880 3470 4105 3495 3620 ...
$ Origin : Factor w/ 2 levels "USA","non-USA": 2 2 2 2 2 1 1 1 1 1 ... $ Make : Factor w/ 93 levels "Acura Integra",..: 1 2 4 3 5 6 7 9 8 10 ...Powyższy wynik pokazuje, że zbiór danych zawiera wiele zmiennych czynnikowych, które można uznać za zmienne kategorialne. W naszym modelu rozważymy zmienne „Poduszki powietrzne” i „Typ”. W tym miejscu staramy się znaleźć jakąkolwiek istotną korelację między typami sprzedawanych samochodów a rodzajem poduszek powietrznych, które posiada. Jeśli zaobserwuje się korelację, możemy oszacować, które typy samochodów mogą lepiej sprzedawać się z typami poduszek powietrznych.
# Load the library.
library("MASS")
# Create a data frame from the main data set.
car.data <- data.frame(Cars93$AirBags, Cars93$Type)
# Create a table with the needed variables.
car.data = table(Cars93$AirBags, Cars93$Type)
print(car.data)
# Perform the Chi-Square test.
print(chisq.test(car.data))Kiedy wykonujemy powyższy kod, daje on następujący wynik -
Compact Large Midsize Small Sporty Van
Driver & Passenger 2 4 7 0 3 0
Driver only 9 7 11 5 8 3
None 5 0 4 16 3 6
Pearson's Chi-squared test
data: car.data
X-squared = 33.001, df = 10, p-value = 0.0002723
Warning message:
In chisq.test(car.data) : Chi-squared approximation may be incorrectWniosek
Wynik pokazuje wartość p mniejszą niż 0,05, co wskazuje na korelację ciągów.