Transformação 2D
Transformação significa transformar alguns gráficos em outra coisa, aplicando regras. Podemos ter vários tipos de transformações, como translação, aumento ou redução, rotação, cisalhamento, etc. Quando uma transformação ocorre em um plano 2D, é chamada de transformação 2D.
As transformações desempenham um papel importante na computação gráfica para reposicionar os gráficos na tela e alterar seu tamanho ou orientação.
Coordenadas Homogêneas
Para realizar uma sequência de transformação, como translação seguida de rotação e dimensionamento, precisamos seguir um processo sequencial -
- Traduza as coordenadas,
- Gire as coordenadas traduzidas e, em seguida,
- Escale as coordenadas giradas para completar a transformação composta.
Para encurtar esse processo, temos que usar a matriz de transformação 3 × 3 em vez da matriz de transformação 2 × 2. Para converter uma matriz 2 × 2 em matriz 3 × 3, temos que adicionar uma coordenada fictícia extra W.
Desta forma, podemos representar o ponto por 3 números em vez de 2 números, que é chamado Homogenous Coordinatesistema. Neste sistema, podemos representar todas as equações de transformação na multiplicação de matrizes. Qualquer ponto cartesiano P (X, Y) pode ser convertido em coordenadas homogêneas por P '(X h , Y h , h).
Tradução
Uma tradução move um objeto para uma posição diferente na tela. Você pode traduzir um ponto em 2D adicionando a coordenada de translação (t x , t y ) à coordenada original (X, Y) para obter a nova coordenada (X ', Y').
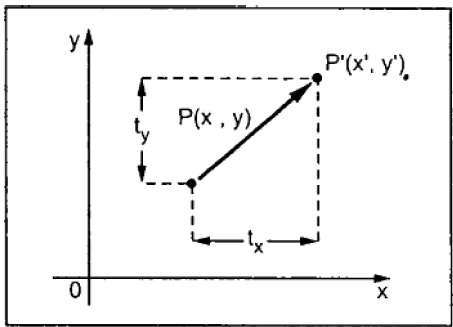
A partir da figura acima, você pode escrever que -
X’ = X + tx
Y’ = Y + ty
O par (t x , t y ) é chamado de vetor de translação ou vetor de deslocamento. As equações acima também podem ser representadas usando os vetores de coluna.
$ P = \ frac {[X]} {[Y]} $ p '= $ \ frac {[X']} {[Y ']} $ T = $ \ frac {[t_ {x}]} {[ t_ {y}]} $
Podemos escrever como -
P’ = P + T
Rotação
Em rotação, giramos o objeto em um ângulo particular θ (theta) de sua origem. Na figura a seguir, podemos ver que o ponto P (X, Y) está localizado no ângulo φ da coordenada X horizontal com a distância r da origem.
Vamos supor que você queira girá-lo no ângulo θ. Depois de girá-lo para um novo local, você obterá um novo ponto P '(X', Y ').

Usando trigonométricas padrão, a coordenada original do ponto P (X, Y) pode ser representada como -
$ X = r \, cos \, \ phi ...... (1) $
$ Y = r \, sin \, \ phi ...... (2) $
Da mesma forma, podemos representar o ponto P '(X', Y ') como -
$ {x} '= r \: cos \: \ left (\ phi \: + \: \ theta \ right) = r \: cos \: \ phi \: cos \: \ theta \: - \: r \ : sin \: \ phi \: sin \: \ theta ....... (3) $
$ {y} '= r \: sin \: \ left (\ phi \: + \: \ theta \ right) = r \: cos \: \ phi \: sin \: \ theta \: + \: r \ : sin \: \ phi \: cos \: \ theta ....... (4) $
Substituindo a equação (1) e (2) em (3) e (4), respectivamente, obteremos
$ {x} '= x \: cos \: \ theta - \: y \: sin \: \ theta $
$ {y} '= x \: sin \: \ theta + \: y \: cos \: \ theta $
Representando a equação acima em forma de matriz,
$$ [X 'Y'] = [XY] \ begin {bmatrix} cos \ theta & sin \ theta \\ −sin \ theta & cos \ theta \ end {bmatrix} OU $$
P '= P. R
Onde R é a matriz de rotação
$$ R = \ begin {bmatrix} cos \ theta & sin \ theta \\ −sin \ theta & cos \ theta \ end {bmatrix} $$
O ângulo de rotação pode ser positivo e negativo.
Para ângulo de rotação positivo, podemos usar a matriz de rotação acima. No entanto, para rotação de ângulo negativo, a matriz mudará conforme mostrado abaixo -
$$ R = \ begin {bmatrix} cos (- \ theta) & sin (- \ theta) \\ -sin (- \ theta) & cos (- \ theta) \ end {bmatrix} $$
$$ = \ begin {bmatrix} cos \ theta & −sin \ theta \\ sin \ theta & cos \ theta \ end {bmatrix} \ left (\ because cos (- \ theta) = cos \ theta \; e \; sin (- \ theta) = −sin \ theta \ right) $$
Dimensionamento
Para alterar o tamanho de um objeto, a transformação de escala é usada. No processo de dimensionamento, você expande ou compacta as dimensões do objeto. A escala pode ser alcançada multiplicando as coordenadas originais do objeto com o fator de escala para obter o resultado desejado.
Vamos supor que as coordenadas originais são (X, Y), os fatores de escala são (S X , S Y ) e as coordenadas produzidas são (X ', Y'). Isso pode ser representado matematicamente conforme mostrado abaixo -
X' = X . SX and Y' = Y . SY
O fator de escala S X , S Y dimensiona o objeto na direção X e Y, respectivamente. As equações acima também podem ser representadas em forma de matriz como abaixo -
$$ \ binom {X '} {Y'} = \ binom {X} {Y} \ begin {bmatrix} S_ {x} & 0 \\ 0 & S_ {y} \ end {bmatrix} $$
OU
P’ = P . S
Onde S é a matriz de escala. O processo de dimensionamento é mostrado na figura a seguir.
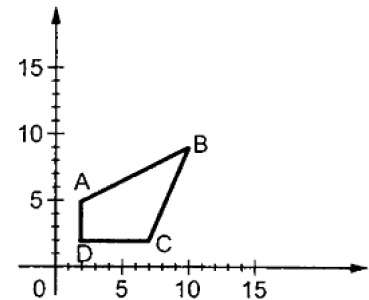
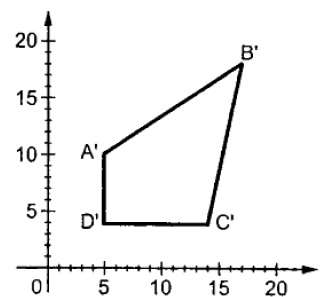
Se fornecermos valores menores que 1 para o fator de escala S, então podemos reduzir o tamanho do objeto. Se fornecermos valores maiores que 1, podemos aumentar o tamanho do objeto.
Reflexão
O reflexo é a imagem espelhada do objeto original. Em outras palavras, podemos dizer que é uma operação de rotação com 180 °. Na transformação de reflexão, o tamanho do objeto não muda.
As figuras a seguir mostram reflexos em relação aos eixos X e Y e sobre a origem, respectivamente.
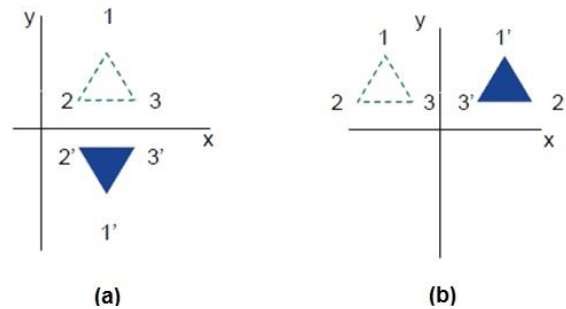
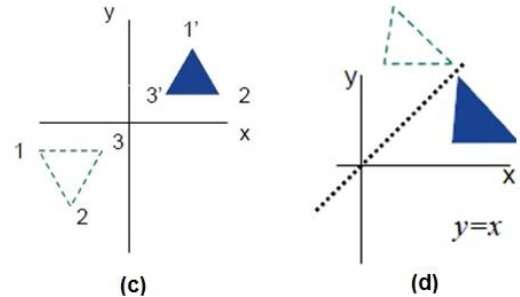
Cisalhamento
Uma transformação que inclina a forma de um objeto é chamada de transformação de cisalhamento. Existem duas transformações de cisalhamentoX-Shear e Y-Shear. Um muda os valores das coordenadas X e o outro muda os valores das coordenadas Y. Contudo; em ambos os casos, apenas uma coordenada muda suas coordenadas e a outra preserva seus valores. O cisalhamento também é denominado comoSkewing.
X-Shear
O X-Shear preserva a coordenada Y e as alterações são feitas nas coordenadas X, o que faz com que as linhas verticais se inclinem para a direita ou para a esquerda, conforme mostrado na figura abaixo.
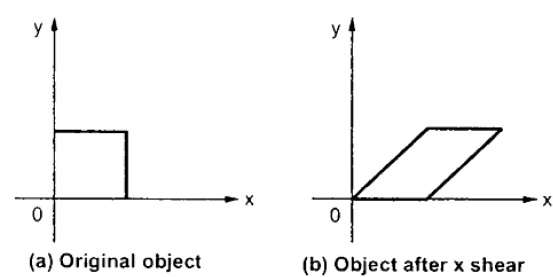
A matriz de transformação para X-Shear pode ser representada como -
$$ X_ {sh} = \ begin {bmatrix} 1 & shx & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} $$
Y '= Y + Sh y . X
X '= X
Y-Shear
O Y-Shear preserva as coordenadas X e altera as coordenadas Y, o que faz com que as linhas horizontais se transformem em linhas inclinadas para cima ou para baixo, conforme mostrado na figura a seguir.
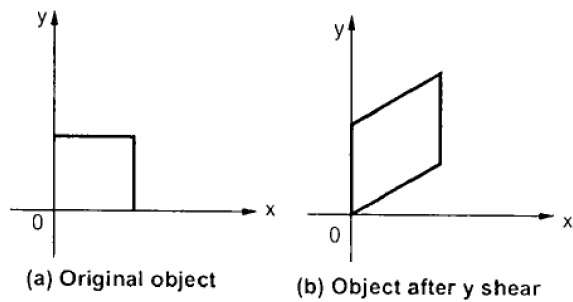
O Y-Shear pode ser representado na matriz como -
$$ Y_ {sh} \ begin {bmatrix} 1 e 0 & 0 \\ shy & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} $$
X '= X + Sh x . Y
Y '= Y
Transformação Composto
Se uma transformação do plano T1 é seguida por uma transformação do segundo plano T2, então o próprio resultado pode ser representado por uma única transformação T que é a composição de T1 e T2 tomada nessa ordem. Isso é escrito como T = T1 ∙ T2.
A transformação composta pode ser alcançada pela concatenação de matrizes de transformação para obter uma matriz de transformação combinada.
Uma matriz combinada -
[T][X] = [X] [T1] [T2] [T3] [T4] …. [Tn]
Onde [Ti] é qualquer combinação de
- Translation
- Scaling
- Shearing
- Rotation
- Reflection
A mudança na ordem de transformação levaria a resultados diferentes, pois em geral a multiplicação de matrizes não é cumulativa, ou seja, [A]. [B] ≠ [B]. [A] e a ordem de multiplicação. O propósito básico de compor transformações é ganhar eficiência aplicando uma única transformação composta a um ponto, em vez de aplicar uma série de transformações, uma após a outra.
Por exemplo, para girar um objeto sobre um ponto arbitrário (X p , Y p ), temos que realizar três etapas -
- Traduzir ponto (X p , Y p ) para a origem.
- Gire sobre a origem.
- Por fim, translade o centro de rotação de volta para onde ele pertencia.