Algoritmo de Geração de Linha

Uma linha conecta dois pontos. É um elemento básico em gráficos. Para desenhar uma linha, você precisa de dois pontos entre os quais você pode desenhar uma linha. Nos três algoritmos a seguir, nos referimos a um ponto da linha como $ X_ {0}, Y_ {0} $ e o segundo ponto da linha como $ X_ {1}, Y_ {1} $.

Algoritmo DDA

O algoritmo Digital Differential Analyzer (DDA) é o algoritmo de geração de linha simples que é explicado passo a passo aqui.

Step 1 - Obtenha a entrada de dois pontos finais $ (X_ {0}, Y_ {0}) $ e $ (X_ {1}, Y_ {1}) $.

Step 2 - Calcule a diferença entre dois pontos finais.

dx = X₁ - X₀
dy = Y₁ - Y₀

Step 3- Com base na diferença calculada na etapa 2, você precisa identificar o número de etapas para colocar o pixel. Se dx> dy, então você precisa de mais etapas na coordenada x; caso contrário, na coordenada y.

if (absolute(dx) > absolute(dy))
   Steps = absolute(dx);
else
   Steps = absolute(dy);

Step 4 - Calcular o incremento na coordenada xey coordenada y.

Xincrement = dx / (float) steps;
Yincrement = dy / (float) steps;

Step 5 - Coloque o pixel incrementando com sucesso as coordenadas xey de acordo e conclua o desenho da linha.

for(int v=0; v < Steps; v++)
{
   x = x + Xincrement;
   y = y + Yincrement;
   putpixel(Round(x), Round(y));
}

Linha Geração de Bresenham

O algoritmo de Bresenham é outro algoritmo de conversão de varredura incremental. A grande vantagem desse algoritmo é que ele usa apenas cálculos inteiros. Movendo-se ao longo do eixo x em intervalos de unidades e em cada etapa, escolha entre duas coordenadas y diferentes.

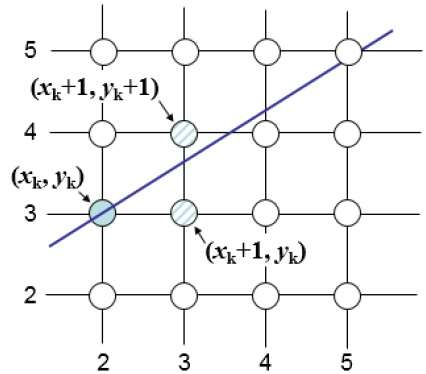
Por exemplo, conforme mostrado na ilustração a seguir, na posição (2, 3) você precisa escolher entre (3, 3) e (3, 4). Você gostaria de ver o ponto mais próximo da linha original.

Na posição de amostra $ X_ {k} + 1, $ as separações verticais da linha matemática são rotuladas como $ d_ {superior} $ e $ d_ {inferior} $.

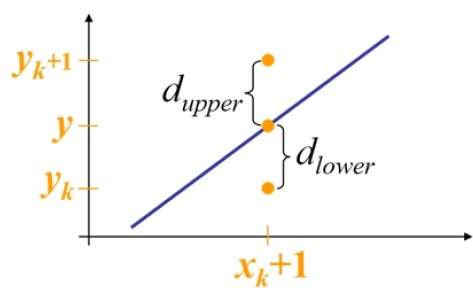
Da ilustração acima, a coordenada y na linha matemática em $ x_ {k} + 1 $ é -

Y = m ($ X_ {k} $ + 1) + b

Assim, $ d_ {superior} $ e $ d_ {inferior} $ são dados da seguinte forma -

$$ d_ {lower} = y-y_ {k} $$

$$ = m (X_ {k} + 1) + b - Y_ {k} $$

$$ d_ {superior} = (y_ {k} + 1) - y $$

$ = Y_ {k} + 1 - m (X_ {k} + 1) - b $

Você pode usá-los para tomar uma decisão simples sobre qual pixel está mais próximo da linha matemática. Esta decisão simples é baseada na diferença entre as duas posições de pixel.

$$ d_ {inferior} - d_ {superior} = 2m (x_ {k} + 1) - 2a_ {k} + 2b - 1 $$

Vamos substituir m por dy / dx onde dx e dy são as diferenças entre os pontos finais.

$$ dx (d_ {inferior} - d_ {superior}) = dx (2 \ frac {\ mathrm {d} y} {\ mathrm {d} x} (x_ {k} + 1) - 2y_ {k} + 2b - 1) $$

$$ = 2dy.x_ {k} - 2dx.y_ {k} + 2dx + 2dx (2b-1) $$

$$ = 2dy.x_ {k} - 2dx.y_ {k} + C $$

Assim, um parâmetro de decisão $ P_ {k} $ para o k- ésimo passo ao longo de uma linha é dado por -

$$ p_ {k} = dx (d_ {inferior} - d_ {superior}) $$

$$ = 2dy.x_ {k} - 2dx.y_ {k} + C $$

O sinal do parâmetro de decisão $ P_ {k} $ é o mesmo que $ d_ {inferior} - d_ {superior} $.

Se $ p_ {k} $ for negativo, então escolha o pixel inferior, caso contrário, escolha o pixel superior.

Lembre-se de que as mudanças de coordenadas ocorrem ao longo do eixo x em etapas unitárias, então você pode fazer tudo com cálculos inteiros. Na etapa k + 1, o parâmetro de decisão é dado como -

$$ p_ {k +1} = 2dy.x_ {k + 1} - 2dx.y_ {k + 1} + C $$

Subtraindo $ p_ {k} $ disto obtemos -

$$ p_ {k + 1} - p_ {k} = 2dy (x_ {k + 1} - x_ {k}) - 2dx (y_ {k + 1} - y_ {k}) $$

Mas, $ x_ {k + 1} $ é o mesmo que $ (xk) + 1 $. Então -

$$ p_ {k + 1} = p_ {k} + 2dy - 2dx (y_ {k + 1} - y_ {k}) $$

Onde, $ Y_ {k + 1} - Y_ {k} $ é 0 ou 1 dependendo do sinal de $ P_ {k} $.

O primeiro parâmetro de decisão $ p_ {0} $ é avaliado em $ (x_ {0}, y_ {0}) $ é dado como -

$$ p_ {0} = 2dy - dx $$

Agora, tendo em mente todos os pontos e cálculos acima, aqui está o algoritmo de Bresenham para inclinação m <1 -

Step 1 - Insira os dois pontos finais da linha, armazenando o ponto final esquerdo em $ (x_ {0}, y_ {0}) $.

Step 2 - Trace o ponto $ (x_ {0}, y_ {0}) $.

Step 3 - Calcule as constantes dx, dy, 2dy e (2dy - 2dx) e obtenha o primeiro valor para o parâmetro de decisão como -

$$ p_ {0} = 2dy - dx $$

Step 4 - A cada $ X_ {k} $ ao longo da linha, começando em k = 0, execute o seguinte teste -

Se $ p_ {k} $ <0, o próximo ponto a traçar é $ (x_ {k} +1, y_ {k}) $ e

$$ p_ {k + 1} = p_ {k} + 2dy $$ Caso contrário,

$$ (x_ {k}, y_ {k} +1) $$

$$ p_ {k + 1} = p_ {k} + 2dy - 2dx $$

Step 5 - Repita o passo 4 (dx - 1) vezes.

Para m> 1, descubra se você precisa incrementar x enquanto incrementa y a cada vez.

Depois de resolver, a equação para o parâmetro de decisão $ P_ {k} $ será muito semelhante, apenas o xey na equação são trocados.

Algoritmo de Ponto Médio

O algoritmo do ponto médio é devido a Bresenham que foi modificado por Pitteway e Van Aken. Suponha que você já tenha colocado o ponto P na coordenada (x, y) e a inclinação da reta seja 0 ≤ k ≤ 1, conforme mostrado na ilustração a seguir.

Agora você precisa decidir se colocar o próximo ponto em E ou N. Isso pode ser escolhido identificando o ponto de interseção Q mais próximo do ponto N ou E. Se o ponto de interseção Q estiver mais próximo do ponto N, então N é considerado como o próximo ponto; caso contrário, E.

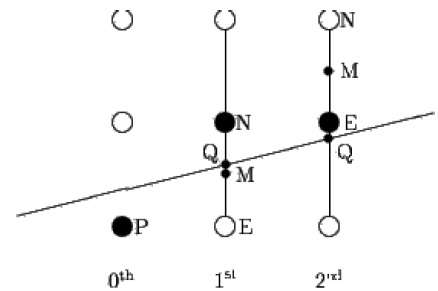
Para determinar isso, primeiro calcule o ponto médio M (x + 1, y + ½). Se o ponto de interseção Q da linha com a linha vertical conectando E e N estiver abaixo de M, considere E como o próximo ponto; caso contrário, tome N como o próximo ponto.

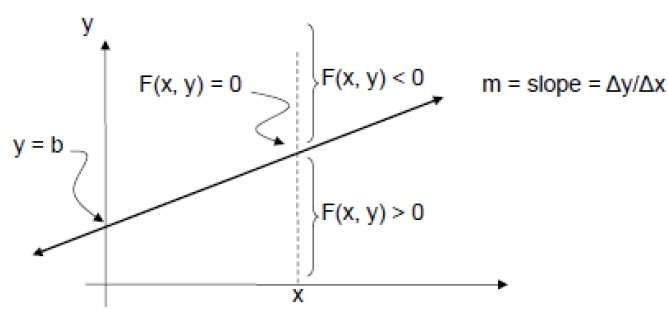
Para verificar isso, precisamos considerar a equação implícita -

F (x, y) = mx + b - y

Para m positivo em qualquer X dado,

Se y estiver na linha, então F (x, y) = 0
Se y estiver acima da linha, então F (x, y) <0
Se y estiver abaixo da linha, então F (x, y)> 0