Algoritmo de Geração de Círculo

Desenhar um círculo na tela é um pouco complexo do que desenhar uma linha. Existem dois algoritmos populares para gerar um círculo -Bresenham’s Algorithm e Midpoint Circle Algorithm. Esses algoritmos são baseados na ideia de determinar os pontos subsequentes necessários para desenhar o círculo. Vamos discutir os algoritmos em detalhes -

A equação do círculo é $ X ^ {2} + Y ^ {2} = r ^ {2}, $ onde r é o raio.

Algoritmo de Bresenham

Não podemos exibir um arco contínuo na exibição raster. Em vez disso, temos que escolher a posição de pixel mais próxima para completar o arco.

Na ilustração a seguir, você pode ver que colocamos o pixel no local (X, Y) e agora precisamos decidir onde colocar o próximo pixel - em N (X + 1, Y) ou em S (X + 1, Y-1).

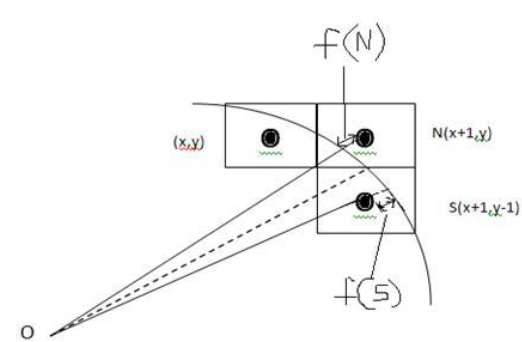
Isso pode ser decidido pelo parâmetro de decisão d.

• Se d <= 0, então N (X + 1, Y) deve ser escolhido como próximo pixel.
• Se d> 0, então S (X + 1, Y-1) deve ser escolhido como o próximo pixel.

Algoritmo

Step 1- Obtenha as coordenadas do centro do círculo e do raio e armazene-as em x, y e R respectivamente. Defina P = 0 e Q = R.

Step 2 - Defina o parâmetro de decisão D = 3 - 2R.

Step 3 - Repita até a etapa 8 enquanto P ≤ Q.

Step 4 - Chame o círculo de desenho (X, Y, P, Q).

Step 5 - Aumente o valor de P.

Step 6 - Se D <0, então D = D + 4P + 6.

Step 7 - Caso contrário, defina R = R - 1, D = D + 4 (PQ) + 10.

Step 8 - Chame o círculo de desenho (X, Y, P, Q).

Draw Circle Method(X, Y, P, Q).

Call Putpixel (X + P, Y + Q).
Call Putpixel (X - P, Y + Q).
Call Putpixel (X + P, Y - Q).
Call Putpixel (X - P, Y - Q).
Call Putpixel (X + Q, Y + P).
Call Putpixel (X - Q, Y + P).
Call Putpixel (X + Q, Y - P).
Call Putpixel (X - Q, Y - P).

Algoritmo de Ponto Médio

Step 1 - Raio de entrada r e círculo centro $ (x_ {c,} y_ {c}) $ e obter o primeiro ponto na circunferência do círculo centrado na origem como

(x0, y0) = (0, r)

Step 2 - Calcule o valor inicial do parâmetro de decisão como

$ P_ {0} $ = 5/4 - r (Veja a seguinte descrição para simplificação desta equação.)

f(x, y) = x2 + y2 - r2 = 0

f(xi - 1/2 + e, yi + 1)
        = (xi - 1/2 + e)2 + (yi + 1)2 - r2 
        = (xi- 1/2)2 + (yi + 1)2 - r2 + 2(xi - 1/2)e + e2
        = f(xi - 1/2, yi + 1) + 2(xi - 1/2)e + e2 = 0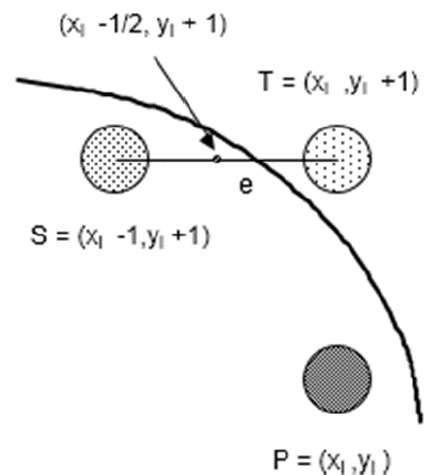

Let di = f(xi - 1/2, yi + 1) = -2(xi - 1/2)e - e2
Thus,

If e < 0 then di > 0 so choose point S = (xi - 1, yi + 1).
di+1    = f(xi - 1 - 1/2, yi + 1 + 1) = ((xi - 1/2) - 1)2 + ((yi + 1) + 1)2 - r2
        = di - 2(xi - 1) + 2(yi + 1) + 1
        = di + 2(yi + 1 - xi + 1) + 1
		  
If e >= 0 then di <= 0 so choose point T = (xi, yi + 1)
   di+1 = f(xi - 1/2, yi + 1 + 1)
       = di + 2yi+1 + 1
		  
The initial value of di is
   d0 = f(r - 1/2, 0 + 1) = (r - 1/2)2 + 12 - r2
      = 5/4 - r {1-r can be used if r is an integer}
		
When point S = (xi - 1, yi + 1) is chosen then
   di+1 = di + -2xi+1 + 2yi+1 + 1
	
When point T = (xi, yi + 1) is chosen then
   di+1 = di + 2yi+1 + 1

Step 3 - Em cada posição $ X_ {K} $ começando em K = 0, execute o seguinte teste -

If PK < 0 then next point on circle (0,0) is (XK+1,YK) and
   PK+1 = PK + 2XK+1 + 1
Else
   PK+1 = PK + 2XK+1 + 1 – 2YK+1
	
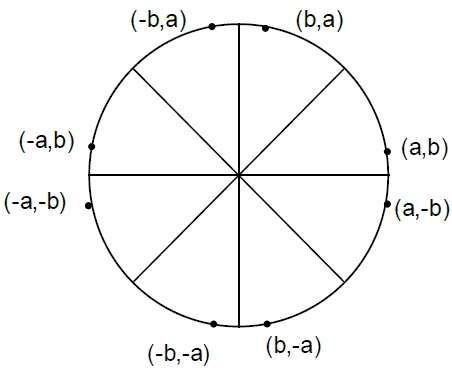
Where, 2XK+1 = 2XK+2 and 2YK+1 = 2YK-2.

Step 4 - Determine os pontos de simetria em outros sete octantes.

Step 5 - Mova cada posição calculada do pixel (X, Y) para o caminho circular centrado em $ (X_ {C,} Y_ {C}) $ e plote os valores das coordenadas.

X = X + XC,   Y = Y + YC

Step 6 - Repita os passos 3 a 5 até X> = Y.