Algoritmo de preenchimento de polígono
Polygon é uma lista ordenada de vértices, conforme mostrado na figura a seguir. Para preencher polígonos com cores específicas, você precisa determinar os pixels que ficam na borda do polígono e aqueles que ficam dentro do polígono. Neste capítulo, veremos como podemos preencher polígonos usando diferentes técnicas.

Scan Line Algorithm
Este algoritmo funciona cruzando a linha de varredura com as bordas do polígono e preenche o polígono entre pares de interseções. As etapas a seguir descrevem como esse algoritmo funciona.
Step 1 - Descubra o Ymin e o Ymax do polígono fornecido.
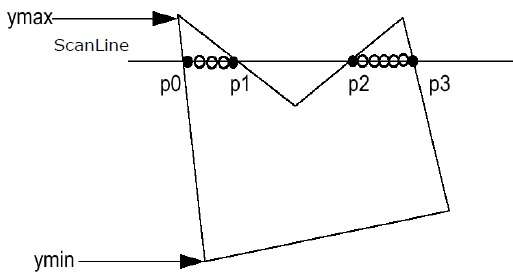
Step 2- ScanLine cruza com cada aresta do polígono de Ymin a Ymax. Nomeie cada ponto de interseção do polígono. Conforme a figura mostrada acima, eles são nomeados como p0, p1, p2, p3.
Step 3 - Classifique o ponto de interseção na ordem crescente da coordenada X, isto é (p0, p1), (p1, p2) e (p2, p3).
Step 4 - Preencha todos os pares de coordenadas que estão dentro dos polígonos e ignore os pares alternativos.
Algoritmo de preenchimento
Às vezes, encontramos um objeto onde queremos preencher a área e seus limites com cores diferentes. Podemos pintar esses objetos com uma cor interior especificada, em vez de procurar uma cor de limite particular como no algoritmo de preenchimento de limite.
Em vez de depender do limite do objeto, ele depende da cor de preenchimento. Em outras palavras, ele substitui a cor interna do objeto pela cor de preenchimento. Quando não houver mais pixels da cor original do interior, o algoritmo estará concluído.
Mais uma vez, esse algoritmo se baseia no método Four-connect ou Eight-connect para preencher os pixels. Mas em vez de procurar a cor do limite, ele está procurando todos os pixels adjacentes que fazem parte do interior.
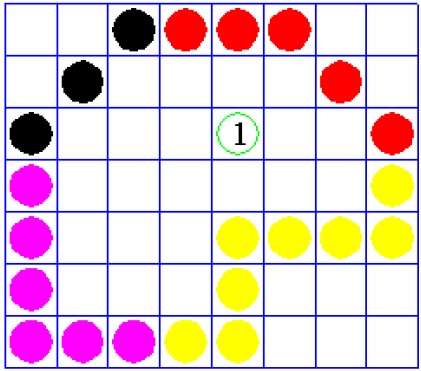
Algoritmo de preenchimento de limite
O algoritmo de preenchimento de limite funciona como seu nome. Esse algoritmo escolhe um ponto dentro de um objeto e começa a preencher até atingir o limite do objeto. A cor do limite e a cor que preenchemos devem ser diferentes para que esse algoritmo funcione.
Nesse algoritmo, assumimos que a cor da fronteira é a mesma para todo o objeto. O algoritmo de preenchimento de limite pode ser implementado por 4 pixels conectados ou 8 pixels conectados.
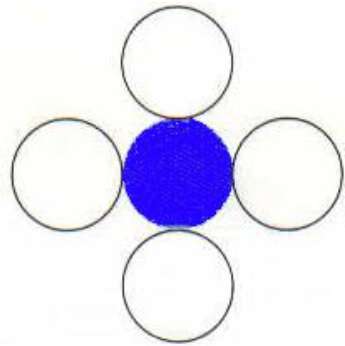
4-polígono conectado
Nesta técnica 4 pixels conectados são usados como mostrado na figura. Estamos colocando os pixels acima, abaixo, à direita e à esquerda dos pixels atuais e esse processo continuará até encontrarmos um limite com cor diferente.
Algoritmo
Step 1 - Inicialize o valor do ponto de semente (seedx, seedy), fcolor e dcol.
Step 2 - Defina os valores limite do polígono.
Step 3 - Verifique se o ponto de semente atual é da cor padrão e repita as etapas 4 e 5 até que os pixels de limite sejam atingidos.
If getpixel(x, y) = dcol then repeat step 4 and 5Step 4 - Altere a cor padrão com a cor de preenchimento no ponto de origem.
setPixel(seedx, seedy, fcol)Step 5 - Siga recursivamente o procedimento com quatro pontos de vizinhança.
FloodFill (seedx – 1, seedy, fcol, dcol)
FloodFill (seedx + 1, seedy, fcol, dcol)
FloodFill (seedx, seedy - 1, fcol, dcol)
FloodFill (seedx – 1, seedy + 1, fcol, dcol)Step 6 - Sair
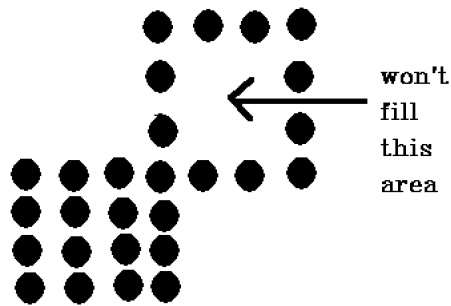
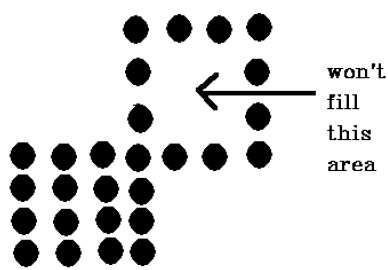
Existe um problema com esta técnica. Considere o caso mostrado abaixo onde tentamos preencher toda a região. Aqui, a imagem é preenchida apenas parcialmente. Nesses casos, a técnica de 4 pixels conectados não pode ser usada.
Polígono 8-conectado
Nesta técnica, 8 pixels conectados são usados conforme mostrado na figura. Estamos colocando pixels acima, abaixo, lado direito e esquerdo dos pixels atuais como fazíamos na técnica de 4 conexões.
Além disso, também colocamos pixels em diagonais para que toda a área do pixel atual seja coberta. Este processo continuará até que encontremos um limite com cor diferente.

Algoritmo
Step 1 - Inicialize o valor do ponto de semente (seedx, seedy), fcolor e dcol.
Step 2 - Defina os valores limite do polígono.
Step 3 - Verifique se o ponto de semente atual é da cor padrão e repita as etapas 4 e 5 até que os pixels de limite sejam atingidos
If getpixel(x,y) = dcol then repeat step 4 and 5Step 4 - Altere a cor padrão com a cor de preenchimento no ponto de origem.
setPixel(seedx, seedy, fcol)Step 5 - Siga recursivamente o procedimento com quatro pontos de vizinhança
FloodFill (seedx – 1, seedy, fcol, dcol)
FloodFill (seedx + 1, seedy, fcol, dcol)
FloodFill (seedx, seedy - 1, fcol, dcol)
FloodFill (seedx, seedy + 1, fcol, dcol)
FloodFill (seedx – 1, seedy + 1, fcol, dcol)
FloodFill (seedx + 1, seedy + 1, fcol, dcol)
FloodFill (seedx + 1, seedy - 1, fcol, dcol)
FloodFill (seedx – 1, seedy - 1, fcol, dcol)Step 6 - Sair
A técnica de 4 pixels conectados falhou em preencher a área marcada na figura a seguir, o que não acontecerá com a técnica de 8 pixels.
Teste de dentro para fora
Este método também é conhecido como counting number method. Ao preencher um objeto, geralmente precisamos identificar se um ponto específico está dentro ou fora do objeto. Existem dois métodos pelos quais podemos identificar se um determinado ponto está dentro ou fora de um objeto.
- Regra ímpar-par
- Regra de enrolamento diferente de zero
Regra ímpar-par
Nesta técnica, contaremos o cruzamento de arestas ao longo da linha de qualquer ponto (x, y) ao infinito. Se o número de interações for ímpar, o ponto (x, y) é um ponto interno; e se o número de interações for par, o ponto (x, y) é um ponto externo. O exemplo a seguir descreve esse conceito.
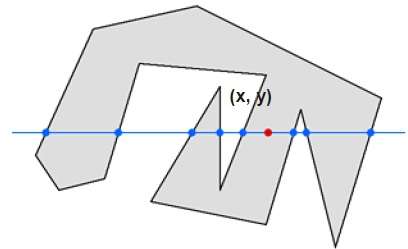
Pela figura acima, podemos ver que do ponto (x, y), o número de pontos de interação no lado esquerdo é 5 e no lado direito é 3. Em ambas as extremidades, o número de pontos de interação é ímpar, o ponto é considerado dentro do objeto.
Regra de número de enrolamento diferente de zero
Este método também é usado com os polígonos simples para testar se o ponto fornecido é interno ou não. Pode ser entendido simplesmente com a ajuda de um alfinete e um elástico. Fixe o pino em uma das bordas do polígono, amarre o elástico nele e estique o elástico ao longo das bordas do polígono.
Quando todas as arestas do polígono estiverem cobertas pelo elástico, verifique o pino que foi fixado no ponto a ser testado. Se encontrarmos pelo menos um vento no ponto, considere-o dentro do polígono, senão podemos dizer que o ponto não está dentro do polígono.
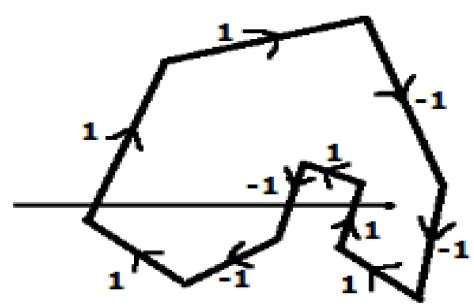
Em outro método alternativo, dê direções para todas as arestas do polígono. Desenhe uma linha de varredura do ponto a ser testado para a extrema esquerda na direção X.
Dê o valor 1 para todas as arestas que estão indo na direção para cima e todos os outros -1 como valores de direção.
Verifique os valores de direção da borda a partir dos quais a linha de varredura está passando e some-os.
Se a soma total deste valor de direção for diferente de zero, então este ponto a ser testado é um interior point, caso contrário, é um exterior point.
Na figura acima, somamos os valores de direção dos quais a linha de varredura está passando, então o total é 1 - 1 + 1 = 1; que é diferente de zero. Portanto, o ponto é considerado um ponto interior.