Fractais de Computação Gráfica
Um matemático francês / americano, Dr. Benoit Mandelbrot, descobriu os Fractais. A palavra fractal deriva de uma palavra latina fractus, que significa quebrado.
O que são fractais?
Fractais são imagens muito complexas geradas por um computador a partir de uma única fórmula. Eles são criados usando iterações. Isso significa que uma fórmula é repetida com valores ligeiramente diferentes continuamente, levando em consideração os resultados da iteração anterior.
Fractais são usados em muitas áreas, como -
Astronomy - Para analisar galáxias, anéis de Saturno, etc.
Biology/Chemistry - Para representar culturas de bactérias, reações químicas, anatomia humana, moléculas, plantas,
Others - Para representar nuvens, litoral e limites, compressão de dados, difusão, economia, arte fractal, música fractal, paisagens, efeitos especiais, etc.

Geração de Fractais
Fractais podem ser gerados repetindo a mesma forma indefinidamente, conforme mostrado na figura a seguir. Na figura (a) mostra um triângulo equilátero. Na figura (b), podemos ver que o triângulo é repetido para criar uma forma de estrela. Na figura (c), podemos ver que a forma de estrela da figura (b) é repetida várias vezes para criar uma nova forma.
Podemos fazer um número ilimitado de iterações para criar a forma desejada. Em termos de programação, a recursão é usada para criar essas formas.

Fractais Geométricos
Fractais geométricos lidam com formas encontradas na natureza que têm dimensões não inteiras ou fractais. Para construir geometricamente um fractal auto-semelhante determinístico (não aleatório), começamos com uma dada forma geométrica, chamada deinitiator. As subpartes do iniciador são então substituídas por um padrão, chamado degenerator.

Por exemplo, se usarmos o iniciador e o gerador mostrados na figura acima, podemos construir um bom padrão repetindo-o. Cada segmento de linha reta no iniciador é substituído por quatro segmentos de linha de comprimento igual em cada etapa. O fator de escala é 1/3, então a dimensão fractal é D = ln 4 / ln 3 ≈ 1,2619.
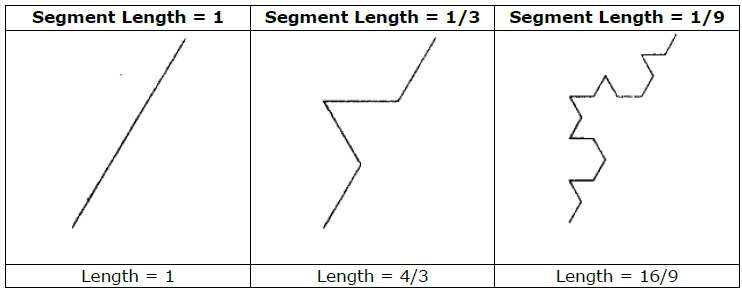
Além disso, o comprimento de cada segmento de linha no iniciador aumenta por um fator de 4/3 em cada etapa, de modo que o comprimento da curva fractal tende ao infinito conforme mais detalhes são adicionados à curva, conforme mostrado na figura a seguir -