Visualização e recorte

O principal uso de recorte em gráficos de computador é remover objetos, linhas ou segmentos de linha que estão fora do painel de exibição. A transformação da visualização é insensível à posição dos pontos em relação ao volume da visualização - especialmente aqueles pontos atrás do visualizador - e é necessário remover esses pontos antes de gerar a visualização.

Point Clipping

Recortar um ponto de uma determinada janela é muito fácil. Considere a figura a seguir, onde o retângulo indica a janela. O recorte de pontos nos diz se o ponto dado (X, Y) está dentro da janela fornecida ou não; e decide se usaremos as coordenadas mínimas e máximas da janela.

A coordenada X do ponto dado está dentro da janela, se X estiver entre Wx1 ≤ X ≤ Wx2. Da mesma forma, a coordenada Y do ponto dado está dentro da janela, se Y estiver entre Wy1 ≤ Y ≤ Wy2.

Recorte de linha

O conceito de recorte de linha é igual ao recorte de ponto. No recorte de linha, vamos cortar a parte da linha que está fora da janela e manter apenas a parte que está dentro da janela.

Cohen-Sutherland Line Clippings

Este algoritmo usa a janela de recorte, conforme mostrado na figura a seguir. A coordenada mínima para a região de recorte é $ (XW_ {min,} YW_ {min}) $ e a coordenada máxima para a região de recorte é $ (XW_ {max,} YW_ {max}) $.

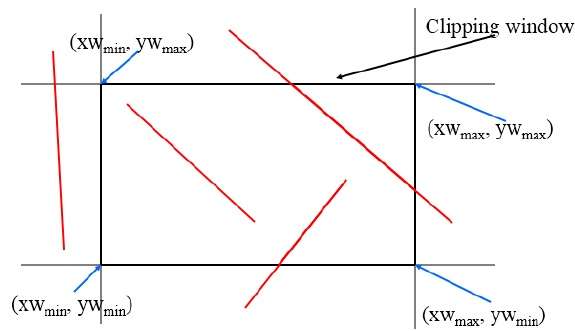
Usaremos 4 bits para dividir toda a região. Esses 4 bits representam as partes superior, inferior, direita e esquerda da região, conforme mostrado na figura a seguir. Aqui oTOP e LEFT bit é definido como 1 porque é o TOP-LEFT canto.

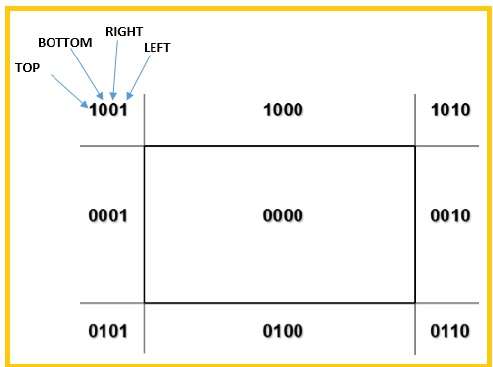
Existem 3 possibilidades para a linha -

A linha pode ficar totalmente dentro da janela (esta linha deve ser aceita).
A linha pode ficar completamente fora da janela (esta linha será completamente removida da região).
A linha pode estar parcialmente dentro da janela (encontraremos o ponto de interseção e desenharemos apenas a parte da linha que está dentro da região).

Algoritmo

Step 1 - Atribua um código de região para cada terminal.

Step 2 - Se ambos os endpoints tiverem um código de região 0000 então aceite esta linha.

Step 3 - Caso contrário, execute o lógico ANDoperação para ambos os códigos de região.

Step 3.1 - Se o resultado não for 0000, em seguida, rejeite a linha.

Step 3.2 - Caso contrário, você precisa de recorte.

Step 3.2.1 - Escolha um ponto final da linha que está fora da janela.

Step 3.2.2 - Encontre o ponto de interseção no limite da janela (com base no código da região).

Step 3.2.3 - Substitua o ponto final pelo ponto de interseção e atualize o código da região.

Step 3.2.4 - Repita o passo 2 até encontrar uma linha recortada aceita ou rejeitada trivialmente.

Step 4 - Repita a etapa 1 para outras linhas.

Algoritmo de recorte de linha de Cyrus-Beck

Este algoritmo é mais eficiente do que o algoritmo de Cohen-Sutherland. Ele emprega representação de linha paramétrica e produtos de ponto simples.

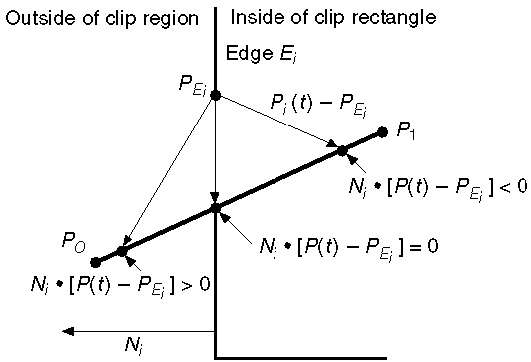
A equação paramétrica da linha é -

P₀P₁:P(t) = P₀ + t(P₁ - P₀)

Seja N _i a aresta normal externa E _i . Agora escolha qualquer ponto arbitrário P _Ei na aresta E _i e o produto escalar N _i . [P (t) - P _Ei ] determina se o ponto P (t) está "dentro da borda do clipe" ou "fora" da borda do clipe ou “Na” borda do clipe.

O ponto P (t) está dentro se N _i . [P (t) - P _Ei ] <0

O ponto P (t) está fora se N _i . [P (t) - P _Ei ]> 0

O ponto P (t) está na aresta se N _i . [P (t) - P _Ei ] = 0 (Ponto de intersecção)

N _i . [P (t) - P _Ei ] = 0

N _i . [P ₀ + t (P ₁ - P ₀ ) - P _Ei ] = 0 (Substituindo P (t) por P ₀ + t (P ₁ - P ₀ ))

N _i . [P ₀ - P _Ei ] + N _i .t [P ₁ - P ₀ ] = 0

N _i . [P ₀ - P _Ei ] + N _i ∙ tD = 0 (substituindo D por [P ₁ - P ₀ ])

N _i . [P ₀ - P _Ei ] = - N _i ∙ tD

A equação para t torna-se,

$$ t = \ tfrac {N_ {i}. [P_ {o} - P_ {Ei}]} {{- N_ {i} .D}} $$

É válido para as seguintes condições -

N _i ≠ 0 (o erro não pode acontecer)
D ≠ 0 (P ₁ ≠ P ₀ )
N _i ∙ D ≠ 0 (P ₀ P ₁ não paralelo a E _i )

Recorte de polígono (algoritmo de Sutherland Hodgman)

Um polígono também pode ser recortado especificando a janela de recorte. O algoritmo de recorte de polígonos de Sutherland Hodgeman é usado para recorte de polígonos. Neste algoritmo, todos os vértices do polígono são recortados contra cada aresta da janela de recorte.

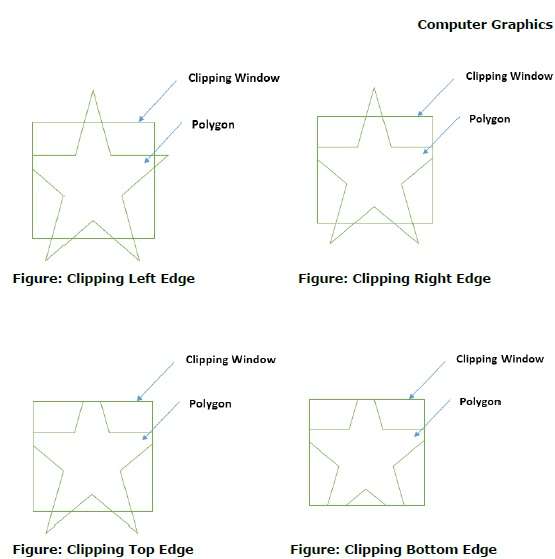
Primeiro, o polígono é recortado contra a borda esquerda da janela do polígono para obter novos vértices do polígono. Esses novos vértices são usados para recortar o polígono contra as arestas direita, superior e inferior da janela de recorte, conforme mostrado na figura a seguir.

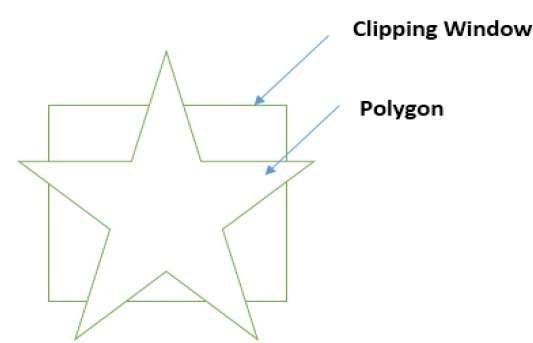
Ao processar uma aresta de um polígono com janela de recorte, um ponto de interseção é encontrado se a aresta não estiver completamente dentro da janela de recorte e uma aresta parcial do ponto de interseção para a aresta externa for recortada. As figuras a seguir mostram recortes das bordas esquerda, direita, superior e inferior -

Recorte de Texto

Várias técnicas são usadas para fornecer recorte de texto em gráficos de computador. Depende dos métodos usados para gerar caracteres e dos requisitos de um determinado aplicativo. Existem três métodos de recorte de texto listados abaixo -

Corte de string tudo ou nada
Recorte de caractere tudo ou nenhum
Recorte de texto

A figura a seguir mostra tudo ou nenhum corte de string -

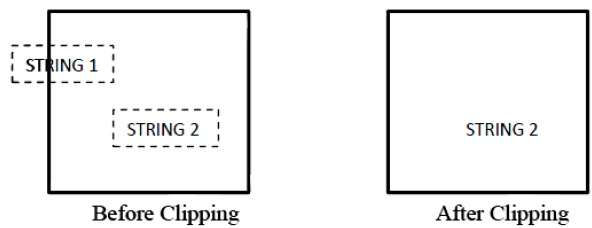
No método de recorte de string tudo ou nenhum, mantemos a string inteira ou rejeitamos toda a string com base na janela de recorte. Conforme mostrado na figura acima, STRING2 está inteiramente dentro da janela de recorte, então nós o mantemos e STRING1 estando apenas parcialmente dentro da janela, rejeitamos.

A figura a seguir mostra todos ou nenhum recorte de caractere -

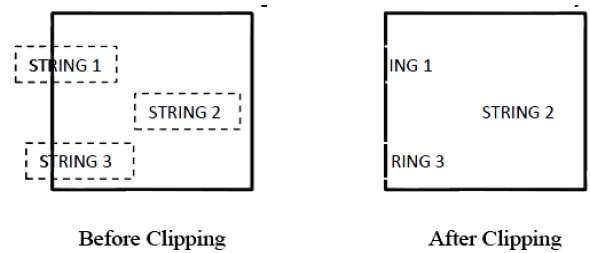
Este método de recorte é baseado em caracteres em vez de string inteira. Neste método, se a string estiver inteiramente dentro da janela de recorte, nós a manteremos. Se estiver parcialmente fora da janela, então -

Você rejeita apenas a parte da corda que está fora
Se o caractere estiver no limite da janela de recorte, descartamos todo o caractere e mantemos a string restante.

A figura a seguir mostra recorte de texto -

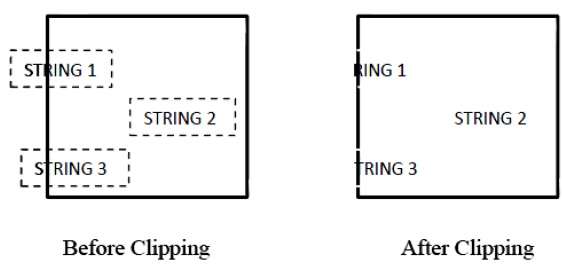
Este método de recorte é baseado em caracteres e não em toda a string. Neste método, se a string estiver inteiramente dentro da janela de recorte, nós a manteremos. Se estiver parcialmente fora da janela, então

Você rejeita apenas a parte do barbante que está fora.
Se o caractere estiver no limite da janela de recorte, descartamos apenas a parte do caractere que está fora da janela de recorte.

Gráficos de bitmap

Um bitmap é uma coleção de pixels que descreve uma imagem. É um tipo de computação gráfica que o computador usa para armazenar e exibir imagens. Neste tipo de gráfico, as imagens são armazenadas bit a bit e, portanto, são denominados gráficos de bitmap. Para melhor compreensão, vamos considerar o exemplo a seguir, onde desenhamos um rosto sorridente usando gráficos de bitmap.

Agora veremos como esse rosto sorridente é armazenado aos poucos na computação gráfica.

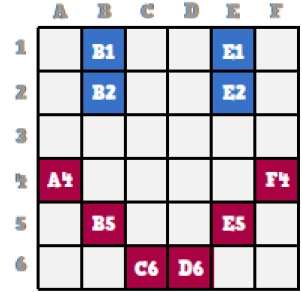
Observando o rosto sorridente original de perto, podemos ver que há duas linhas azuis representadas como B1, B2 e E1, E2 na figura acima.

Da mesma forma, o smiley é representado usando a combinação de bits de A4, B5, C6, D6, E5 e F4 respectivamente.

As principais desvantagens dos gráficos de bitmap são -

Não podemos redimensionar a imagem bitmap. Se você tentar redimensionar, os pixels ficam borrados.
Os bitmaps coloridos podem ser muito grandes.