R - Regressão Linear

A análise de regressão é uma ferramenta estatística amplamente utilizada para estabelecer um modelo de relacionamento entre duas variáveis. Uma dessas variáveis é chamada de variável preditora, cujo valor é obtido por meio de experimentos. A outra variável é chamada de variável de resposta, cujo valor é derivado da variável preditora.

Na Regressão Linear, essas duas variáveis são relacionadas por meio de uma equação, onde o expoente (potência) de ambas as variáveis é 1. Matematicamente, uma relação linear representa uma linha reta quando plotada como um gráfico. Uma relação não linear em que o expoente de qualquer variável não é igual a 1 cria uma curva.

A equação matemática geral para uma regressão linear é -

y = ax + b

A seguir está a descrição dos parâmetros usados -

y é a variável de resposta.
x é a variável preditora.
a e b são constantes que são chamadas de coeficientes.

Passos para estabelecer uma regressão

Um exemplo simples de regressão é prever o peso de uma pessoa quando sua altura é conhecida. Para fazer isso, precisamos ter a relação entre altura e peso de uma pessoa.

As etapas para criar o relacionamento são -

Faça a experiência de recolher uma amostra dos valores observados de altura e peso correspondente.
Crie um modelo de relacionamento usando o lm() funções em R.
Encontre os coeficientes do modelo criado e crie a equação matemática usando estes
Obtenha um resumo do modelo de relacionamento para saber o erro médio na previsão. Também chamadoresiduals.
Para prever o peso de novas pessoas, use o predict() função em R.

Dados de entrada

Abaixo estão os dados de amostra que representam as observações -

# Values of height
151, 174, 138, 186, 128, 136, 179, 163, 152, 131

# Values of weight.
63, 81, 56, 91, 47, 57, 76, 72, 62, 48

Função lm ()

Esta função cria o modelo de relacionamento entre o preditor e a variável de resposta.

Sintaxe

A sintaxe básica para lm() função na regressão linear é -

lm(formula,data)

A seguir está a descrição dos parâmetros usados -

formula é um símbolo que apresenta a relação entre x e y.
data é o vetor no qual a fórmula será aplicada.

Crie um modelo de relacionamento e obtenha os coeficientes

x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)

# Apply the lm() function.
relation <- lm(y~x)

print(relation)

Quando executamos o código acima, ele produz o seguinte resultado -

Call:
lm(formula = y ~ x)

Coefficients:
(Intercept)            x  
   -38.4551          0.6746

Obtenha o Resumo do Relacionamento

x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)

# Apply the lm() function.
relation <- lm(y~x)

print(summary(relation))

Quando executamos o código acima, ele produz o seguinte resultado -

Call:
lm(formula = y ~ x)

Residuals:
    Min      1Q     Median      3Q     Max 
-6.3002    -1.6629  0.0412    1.8944  3.9775 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -38.45509    8.04901  -4.778  0.00139 ** 
x             0.67461    0.05191  12.997 1.16e-06 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.253 on 8 degrees of freedom
Multiple R-squared:  0.9548,    Adjusted R-squared:  0.9491 
F-statistic: 168.9 on 1 and 8 DF,  p-value: 1.164e-06

Função Predict ()

Sintaxe

A sintaxe básica para predizer () em regressão linear é -

predict(object, newdata)

A seguir está a descrição dos parâmetros usados -

object é a fórmula que já foi criada usando a função lm ().
newdata é o vetor que contém o novo valor para a variável preditora.

Preveja o peso de novas pessoas

# The predictor vector.
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)

# The resposne vector.
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)

# Apply the lm() function.
relation <- lm(y~x)

# Find weight of a person with height 170.
a <- data.frame(x = 170)
result <-  predict(relation,a)
print(result)

Quando executamos o código acima, ele produz o seguinte resultado -

1 
76.22869

Visualize a regressão graficamente

# Create the predictor and response variable.
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
relation <- lm(y~x)

# Give the chart file a name.
png(file = "linearregression.png")

# Plot the chart.
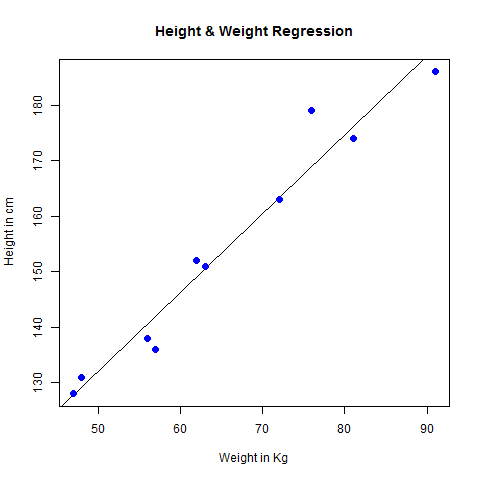
plot(y,x,col = "blue",main = "Height & Weight Regression",
abline(lm(x~y)),cex = 1.3,pch = 16,xlab = "Weight in Kg",ylab = "Height in cm")

# Save the file.
dev.off()

Quando executamos o código acima, ele produz o seguinte resultado -