R - Guia Rápido
R é uma linguagem de programação e ambiente de software para análise estatística, representação gráfica e relatórios. R foi criado por Ross Ihaka e Robert Gentleman na University of Auckland, Nova Zelândia, e atualmente é desenvolvido pela R Development Core Team.
O núcleo de R é uma linguagem de computador interpretada que permite ramificação e loop, bem como programação modular usando funções. R permite a integração com os procedimentos escritos nas linguagens C, C ++, .Net, Python ou FORTRAN para maior eficiência.
R está disponível gratuitamente sob a GNU General Public License, e versões binárias pré-compiladas são fornecidas para vários sistemas operacionais como Linux, Windows e Mac.
R é um software livre distribuído sob uma cópia deixada no estilo GNU, e uma parte oficial do projeto GNU chamada GNU S.
Evolução de R
R foi inicialmente escrito por Ross Ihaka e Robert Gentlemanno Departamento de Estatística da Universidade de Auckland em Auckland, Nova Zelândia. R fez sua primeira aparição em 1993.
Um grande grupo de pessoas contribuiu para o R enviando códigos e relatórios de erros.
Desde meados de 1997, existe um grupo principal (o "R Core Team") que pode modificar o arquivo de código-fonte do R.
Características de R
Conforme afirmado anteriormente, R é uma linguagem de programação e ambiente de software para análise estatística, representação gráfica e relatórios. A seguir estão as características importantes do R -
R é uma linguagem de programação bem desenvolvida, simples e eficaz que inclui condicionais, loops, funções recursivas definidas pelo usuário e recursos de entrada e saída.
R tem uma facilidade de manuseio e armazenamento de dados eficaz
R fornece um conjunto de operadores para cálculos em matrizes, listas, vetores e matrizes.
R fornece uma coleção grande, coerente e integrada de ferramentas para análise de dados.
R fornece recursos gráficos para análise e exibição de dados diretamente no computador ou impressão nos jornais.
Como conclusão, R é a linguagem de programação de estatísticas mais amplamente usada no mundo. É a escolha número 1 de cientistas de dados e é apoiado por uma comunidade vibrante e talentosa de colaboradores. R é ensinado em universidades e implantado em aplicativos de negócios de missão crítica. Este tutorial irá ensinar a programação R junto com exemplos adequados em etapas simples e fáceis.
Configuração de ambiente local
Se você ainda deseja configurar seu ambiente para R, siga as etapas abaixo.
Instalação Windows
Você pode baixar a versão do instalador do Windows de R de R-3.2.2 para Windows (32/64 bits) e salvá-lo em um diretório local.
Por se tratar de um instalador do Windows (.exe) com o nome "R-version-win.exe". Você pode apenas clicar duas vezes e executar o instalador aceitando as configurações padrão. Se o seu Windows for de 32 bits, ele instala a versão de 32 bits. Mas se o seu Windows for de 64 bits, ele instala as versões de 32 e 64 bits.
Após a instalação, você pode localizar o ícone para executar o Programa em uma estrutura de diretório "R \ R3.2.2 \ bin \ i386 \ Rgui.exe" nos Arquivos de Programas do Windows. Clicar neste ícone exibe o R-GUI que é o console R para fazer a programação R.
Instalação Linux
R está disponível como um binário para muitas versões do Linux no local R Binaries .
A instrução para instalar o Linux varia de um tipo para outro. Essas etapas são mencionadas em cada tipo de versão do Linux no link mencionado. No entanto, se você estiver com pressa, pode usaryum comando para instalar o R da seguinte forma -
$ yum install RO comando acima instalará a funcionalidade principal da programação R junto com os pacotes padrão, mas você ainda precisa de um pacote adicional, então você pode iniciar o prompt R da seguinte maneira -
$ R
R version 3.2.0 (2015-04-16) -- "Full of Ingredients"
Copyright (C) 2015 The R Foundation for Statistical Computing
Platform: x86_64-redhat-linux-gnu (64-bit)
R is free software and comes with ABSOLUTELY NO WARRANTY.
You are welcome to redistribute it under certain conditions.
Type 'license()' or 'licence()' for distribution details.
R is a collaborative project with many contributors.
Type 'contributors()' for more information and
'citation()' on how to cite R or R packages in publications.
Type 'demo()' for some demos, 'help()' for on-line help, or
'help.start()' for an HTML browser interface to help.
Type 'q()' to quit R.
>Agora você pode usar o comando install no prompt R para instalar o pacote necessário. Por exemplo, o seguinte comando irá instalarplotrix pacote que é necessário para gráficos 3D.
> install.packages("plotrix")Como convenção, começaremos a aprender programação R escrevendo um "Hello, World!" programa. Dependendo das necessidades, você pode programar no prompt de comando R ou pode usar um arquivo de script R para escrever seu programa. Vamos verificar um por um.
Prompt de Comando R
Depois de configurar o ambiente R, é fácil iniciar o prompt de comando R apenas digitando o seguinte comando no prompt de comando -
$ RIsso iniciará o interpretador R e você receberá um prompt> onde você pode começar a digitar seu programa da seguinte maneira -
> myString <- "Hello, World!"
> print ( myString)
[1] "Hello, World!"Aqui, a primeira instrução define uma variável de string myString, onde atribuímos uma string "Hello, World!" e a próxima instrução print () está sendo usada para imprimir o valor armazenado na variável myString.
Arquivo de script R
Normalmente, você fará sua programação escrevendo seus programas em arquivos de script e, em seguida, executará esses scripts em seu prompt de comando com a ajuda de um interpretador R chamado Rscript. Então, vamos começar escrevendo o seguinte código em um arquivo de texto chamado test.R como em -
# My first program in R Programming
myString <- "Hello, World!"
print ( myString)Salve o código acima em um arquivo test.R e execute-o no prompt de comando do Linux conforme mostrado abaixo. Mesmo se você estiver usando o Windows ou outro sistema, a sintaxe permanecerá a mesma.
$ Rscript test.RQuando executamos o programa acima, ele produz o seguinte resultado.
[1] "Hello, World!"Comentários
Os comentários são como texto de ajuda em seu programa R e são ignorados pelo interpretador durante a execução de seu programa real. Um único comentário é escrito usando # no início da instrução da seguinte forma -
# My first program in R ProgrammingR não oferece suporte a comentários de várias linhas, mas você pode executar um truque que é o seguinte -
if(FALSE) {
"This is a demo for multi-line comments and it should be put inside either a
single OR double quote"
}
myString <- "Hello, World!"
print ( myString)[1] "Hello, World!"Embora os comentários acima sejam executados pelo intérprete R, eles não interferirão no seu programa real. Você deve colocar esses comentários dentro, entre aspas simples ou duplas.
Geralmente, ao programar em qualquer linguagem de programação, você precisa usar várias variáveis para armazenar várias informações. As variáveis nada mais são do que locais de memória reservados para armazenar valores. Isso significa que, ao criar uma variável, você reserva algum espaço na memória.
Você pode gostar de armazenar informações de vários tipos de dados como caractere, caractere largo, inteiro, ponto flutuante, ponto flutuante duplo, Booleano etc. Com base no tipo de dados de uma variável, o sistema operacional aloca memória e decide o que pode ser armazenado no memória reservada.
Em contraste com outras linguagens de programação como C e java em R, as variáveis não são declaradas como algum tipo de dados. As variáveis são atribuídas com objetos R e o tipo de dados do objeto R torna-se o tipo de dados da variável. Existem muitos tipos de objetos-R. Os mais usados são -
- Vectors
- Lists
- Matrices
- Arrays
- Factors
- Frames de dados
O mais simples desses objetos é o vector objecte existem seis tipos de dados desses vetores atômicos, também denominados como seis classes de vetores. Os outros objetos-R são construídos sobre os vetores atômicos.
| Tipo de dados | Exemplo | Verificar |
|---|---|---|
| Lógico | VERDADEIRO FALSO |
produz o seguinte resultado - |
| Numérico | 12,3, 5, 999 |
produz o seguinte resultado - |
| Inteiro | 2L, 34L, 0L |
produz o seguinte resultado - |
| Complexo | 3 + 2i |
produz o seguinte resultado - |
| Personagem | 'a', '"bom", "VERDADEIRO", '23 .4' |
produz o seguinte resultado - |
| Cru | "Olá" é armazenado como 48 65 6c 6c 6f |
produz o seguinte resultado - |
Na programação R, os tipos de dados mais básicos são os objetos R chamados vectorsque contém elementos de diferentes classes, conforme mostrado acima. Observe que em R o número de classes não se limita apenas aos seis tipos acima. Por exemplo, podemos usar muitos vetores atômicos e criar um array cuja classe se tornará array.
Vetores
Quando você deseja criar um vetor com mais de um elemento, você deve usar c() função que significa combinar os elementos em um vetor.
# Create a vector.
apple <- c('red','green',"yellow")
print(apple)
# Get the class of the vector.
print(class(apple))Quando executamos o código acima, ele produz o seguinte resultado -
[1] "red" "green" "yellow"
[1] "character"Listas
Uma lista é um objeto R que pode conter muitos tipos diferentes de elementos dentro dele, como vetores, funções e até mesmo outra lista dentro dele.
# Create a list.
list1 <- list(c(2,5,3),21.3,sin)
# Print the list.
print(list1)Quando executamos o código acima, ele produz o seguinte resultado -
[[1]]
[1] 2 5 3
[[2]]
[1] 21.3
[[3]]
function (x) .Primitive("sin")Matrizes
Uma matriz é um conjunto de dados retangular bidimensional. Ele pode ser criado usando uma entrada vetorial para a função de matriz.
# Create a matrix.
M = matrix( c('a','a','b','c','b','a'), nrow = 2, ncol = 3, byrow = TRUE)
print(M)Quando executamos o código acima, ele produz o seguinte resultado -
[,1] [,2] [,3]
[1,] "a" "a" "b"
[2,] "c" "b" "a"Arrays
Enquanto as matrizes estão confinadas a duas dimensões, os arrays podem ter qualquer número de dimensões. A função array tem um atributo dim que cria o número necessário de dimensões. No exemplo abaixo, criamos um array com dois elementos que são matrizes 3x3 cada.
# Create an array.
a <- array(c('green','yellow'),dim = c(3,3,2))
print(a)Quando executamos o código acima, ele produz o seguinte resultado -
, , 1
[,1] [,2] [,3]
[1,] "green" "yellow" "green"
[2,] "yellow" "green" "yellow"
[3,] "green" "yellow" "green"
, , 2
[,1] [,2] [,3]
[1,] "yellow" "green" "yellow"
[2,] "green" "yellow" "green"
[3,] "yellow" "green" "yellow"Fatores
Fatores são os objetos r que são criados usando um vetor. Ele armazena o vetor junto com os valores distintos dos elementos no vetor como rótulos. Os rótulos são sempre caracteres, independentemente de serem numéricos, caracteres ou booleanos etc. no vetor de entrada. Eles são úteis na modelagem estatística.
Fatores são criados usando o factor()função. onlevels funções fornece a contagem de níveis.
# Create a vector.
apple_colors <- c('green','green','yellow','red','red','red','green')
# Create a factor object.
factor_apple <- factor(apple_colors)
# Print the factor.
print(factor_apple)
print(nlevels(factor_apple))Quando executamos o código acima, ele produz o seguinte resultado -
[1] green green yellow red red red green
Levels: green red yellow
[1] 3Frames de dados
Os quadros de dados são objetos de dados tabulares. Ao contrário de uma matriz no quadro de dados, cada coluna pode conter diferentes modos de dados. A primeira coluna pode ser numérica, enquanto a segunda coluna pode ser de caracteres e a terceira coluna pode ser lógica. É uma lista de vetores de igual comprimento.
Quadros de dados são criados usando o data.frame() função.
# Create the data frame.
BMI <- data.frame(
gender = c("Male", "Male","Female"),
height = c(152, 171.5, 165),
weight = c(81,93, 78),
Age = c(42,38,26)
)
print(BMI)Quando executamos o código acima, ele produz o seguinte resultado -
gender height weight Age
1 Male 152.0 81 42
2 Male 171.5 93 38
3 Female 165.0 78 26Uma variável nos fornece armazenamento nomeado que nossos programas podem manipular. Uma variável em R pode armazenar um vetor atômico, grupo de vetores atômicos ou uma combinação de muitos Robjects. Um nome de variável válido consiste em letras, números e pontos ou caracteres sublinhados. O nome da variável começa com uma letra ou o ponto não seguido por um número.
| Nome variável | Validade | Razão |
|---|---|---|
| var_name2. | válido | Possui letras, números, ponto e sublinhado |
| var_name% | Inválido | Possui o caractere '%'. Somente ponto (.) E sublinhado são permitidos. |
| 2var_name | inválido | Começa com um número |
.var_name, var.name |
válido | Pode começar com um ponto (.), Mas o ponto (.) Não deve ser seguido por um número. |
| .2var_name | inválido | O ponto inicial é seguido por um número que o torna inválido. |
| _var_name | inválido | Começa com _ que não é válido |
Atribuição de Variável
As variáveis podem receber valores atribuídos usando o operador left, right e igual a. Os valores das variáveis podem ser impressos usandoprint() ou cat()função. ocat() função combina vários itens em uma saída de impressão contínua.
# Assignment using equal operator.
var.1 = c(0,1,2,3)
# Assignment using leftward operator.
var.2 <- c("learn","R")
# Assignment using rightward operator.
c(TRUE,1) -> var.3
print(var.1)
cat ("var.1 is ", var.1 ,"\n")
cat ("var.2 is ", var.2 ,"\n")
cat ("var.3 is ", var.3 ,"\n")Quando executamos o código acima, ele produz o seguinte resultado -
[1] 0 1 2 3
var.1 is 0 1 2 3
var.2 is learn R
var.3 is 1 1Note- O vetor c (TRUE, 1) possui uma combinação de classes lógicas e numéricas. Portanto, a classe lógica é forçada a uma classe numérica, tornando TRUE como 1.
Tipo de dados de uma variável
Em R, uma variável em si não é declarada de nenhum tipo de dados, em vez disso, ela obtém o tipo de dados do objeto R atribuído a ela. Portanto, R é chamada de linguagem de tipo dinâmico, o que significa que podemos alterar o tipo de dados de uma variável da mesma variável repetidamente ao usá-la em um programa.
var_x <- "Hello"
cat("The class of var_x is ",class(var_x),"\n")
var_x <- 34.5
cat(" Now the class of var_x is ",class(var_x),"\n")
var_x <- 27L
cat(" Next the class of var_x becomes ",class(var_x),"\n")Quando executamos o código acima, ele produz o seguinte resultado -
The class of var_x is character
Now the class of var_x is numeric
Next the class of var_x becomes integerEncontrando Variáveis
Para saber todas as variáveis atualmente disponíveis na área de trabalho, usamos o ls()função. Além disso, a função ls () pode usar padrões para combinar os nomes das variáveis.
print(ls())Quando executamos o código acima, ele produz o seguinte resultado -
[1] "my var" "my_new_var" "my_var" "var.1"
[5] "var.2" "var.3" "var.name" "var_name2."
[9] "var_x" "varname"Note - É uma saída de amostra dependendo de quais variáveis são declaradas em seu ambiente.
A função ls () pode usar padrões para combinar os nomes das variáveis.
# List the variables starting with the pattern "var".
print(ls(pattern = "var"))Quando executamos o código acima, ele produz o seguinte resultado -
[1] "my var" "my_new_var" "my_var" "var.1"
[5] "var.2" "var.3" "var.name" "var_name2."
[9] "var_x" "varname"As variáveis começando com dot(.) estão ocultos, eles podem ser listados usando o argumento "all.names = TRUE" para a função ls ().
print(ls(all.name = TRUE))Quando executamos o código acima, ele produz o seguinte resultado -
[1] ".cars" ".Random.seed" ".var_name" ".varname" ".varname2"
[6] "my var" "my_new_var" "my_var" "var.1" "var.2"
[11]"var.3" "var.name" "var_name2." "var_x"Excluindo Variáveis
As variáveis podem ser excluídas usando o rm()função. Abaixo, excluímos a variável var.3. Ao imprimir o valor do erro da variável é lançado.
rm(var.3)
print(var.3)Quando executamos o código acima, ele produz o seguinte resultado -
[1] "var.3"
Error in print(var.3) : object 'var.3' not foundTodas as variáveis podem ser excluídas usando o rm() e ls() funcionam juntos.
rm(list = ls())
print(ls())Quando executamos o código acima, ele produz o seguinte resultado -
character(0)Um operador é um símbolo que informa ao compilador para executar manipulações matemáticas ou lógicas específicas. A linguagem R é rica em operadores integrados e fornece os seguintes tipos de operadores.
Tipos de Operadores
Temos os seguintes tipos de operadores na programação R -
- Operadores aritméticos
- Operadores Relacionais
- Operadores lógicos
- Operadores de atribuição
- Operadores diversos
Operadores aritméticos
A tabela a seguir mostra os operadores aritméticos suportados pela linguagem R. Os operadores atuam em cada elemento do vetor.
| Operador | Descrição | Exemplo |
|---|---|---|
| + | Adiciona dois vetores |
produz o seguinte resultado - |
| - | Subtrai o segundo vetor do primeiro |
produz o seguinte resultado - |
| * | Multiplica os dois vetores |
produz o seguinte resultado - |
| / | Divida o primeiro vetor com o segundo |
Quando executamos o código acima, ele produz o seguinte resultado - |
| %% | Dê o restante do primeiro vetor com o segundo |
produz o seguinte resultado - |
| % /% | O resultado da divisão do primeiro vetor com o segundo (quociente) |
produz o seguinte resultado - |
| ^ | O primeiro vetor elevado ao expoente do segundo vetor |
produz o seguinte resultado - |
Operadores Relacionais
A tabela a seguir mostra os operadores relacionais suportados pela linguagem R. Cada elemento do primeiro vetor é comparado com o elemento correspondente do segundo vetor. O resultado da comparação é um valor booleano.
| Operador | Descrição | Exemplo |
|---|---|---|
| > | Verifica se cada elemento do primeiro vetor é maior que o elemento correspondente do segundo vetor. |
produz o seguinte resultado - |
| < | Verifica se cada elemento do primeiro vetor é menor que o elemento correspondente do segundo vetor. |
produz o seguinte resultado - |
| == | Verifica se cada elemento do primeiro vetor é igual ao elemento correspondente do segundo vetor. |
produz o seguinte resultado - |
| <= | Verifica se cada elemento do primeiro vetor é menor ou igual ao elemento correspondente do segundo vetor. |
produz o seguinte resultado - |
| > = | Verifica se cada elemento do primeiro vetor é maior ou igual ao elemento correspondente do segundo vetor. |
produz o seguinte resultado - |
| ! = | Verifica se cada elemento do primeiro vetor é diferente do elemento correspondente do segundo vetor. |
produz o seguinte resultado - |
Operadores lógicos
A tabela a seguir mostra os operadores lógicos suportados pela linguagem R. É aplicável apenas a vetores do tipo lógico, numérico ou complexo. Todos os números maiores que 1 são considerados como valor lógico VERDADEIRO.
Cada elemento do primeiro vetor é comparado com o elemento correspondente do segundo vetor. O resultado da comparação é um valor booleano.
| Operador | Descrição | Exemplo |
|---|---|---|
| E | É chamado de operador E lógico elementar. Ele combina cada elemento do primeiro vetor com o elemento correspondente do segundo vetor e dá uma saída TRUE se ambos os elementos forem TRUE. |
produz o seguinte resultado - |
| | | É chamado de operador OR lógico elementar. Ele combina cada elemento do primeiro vetor com o elemento correspondente do segundo vetor e dá uma saída TRUE se um dos elementos for TRUE. |
produz o seguinte resultado - |
| ! | É chamado de operador lógico NOT. Pega cada elemento do vetor e fornece o valor lógico oposto. |
produz o seguinte resultado - |
O operador lógico && e || considera apenas o primeiro elemento dos vetores e fornece um vetor de elemento único como saída.
| Operador | Descrição | Exemplo |
|---|---|---|
| && | Operador lógico chamado AND. Pega o primeiro elemento de ambos os vetores e dá o VERDADEIRO apenas se ambos forem VERDADEIROS. |
produz o seguinte resultado - |
| || | Operador lógico chamado OR. Pega o primeiro elemento de ambos os vetores e dá TRUE se um deles for TRUE. |
produz o seguinte resultado - |
Operadores de atribuição
Esses operadores são usados para atribuir valores aos vetores.
| Operador | Descrição | Exemplo |
|---|---|---|
| <- ou = ou << - |
Atribuição Chamada de Esquerda |
produz o seguinte resultado - |
| -> ou - >> |
Atribuição Chamada de Direito |
produz o seguinte resultado - |
Operadores diversos
Esses operadores são usados para fins específicos e não para cálculos matemáticos ou lógicos gerais.
| Operador | Descrição | Exemplo |
|---|---|---|
| : | Operador de cólon. Ele cria a série de números em sequência para um vetor. |
produz o seguinte resultado - |
| %dentro% | Este operador é usado para identificar se um elemento pertence a um vetor. |
produz o seguinte resultado - |
| % *% | Este operador é usado para multiplicar uma matriz com sua transposta. |
produz o seguinte resultado - |
As estruturas de tomada de decisão requerem que o programador especifique uma ou mais condições a serem avaliadas ou testadas pelo programa, juntamente com uma instrução ou instruções a serem executadas se a condição for determinada como truee, opcionalmente, outras instruções a serem executadas se a condição for determinada como false.
A seguir está a forma geral de uma estrutura típica de tomada de decisão encontrada na maioria das linguagens de programação -
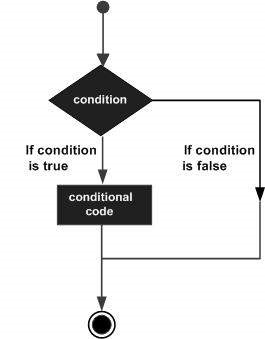
R fornece os seguintes tipos de declarações de tomada de decisão. Clique nos links a seguir para verificar seus detalhes.
| Sr. Não. | Declaração e descrição |
|---|---|
| 1 | declaração if A if declaração consiste em uma expressão booleana seguida por uma ou mais declarações. |
| 2 | declaração if ... else A if declaração pode ser seguida por um opcional else instrução, que é executada quando a expressão booleana é falsa. |
| 3 | declaração switch UMA switch instrução permite que uma variável seja testada quanto à igualdade em relação a uma lista de valores. |
Pode haver uma situação em que você precise executar um bloco de código várias vezes. Em geral, as instruções são executadas sequencialmente. A primeira instrução em uma função é executada primeiro, seguida pela segunda e assim por diante.
As linguagens de programação fornecem várias estruturas de controle que permitem caminhos de execução mais complicados.
Uma instrução de loop nos permite executar uma instrução ou grupo de instruções várias vezes e o seguinte é a forma geral de uma instrução de loop na maioria das linguagens de programação -
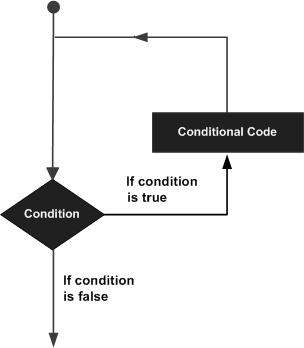
A linguagem de programação R fornece os seguintes tipos de loop para lidar com os requisitos de loop. Clique nos links a seguir para verificar seus detalhes.
| Sr. Não. | Tipo de Loop e Descrição |
|---|---|
| 1 | loop de repetição Executa uma sequência de instruções várias vezes e abrevia o código que gerencia a variável de loop. |
| 2 | loop while Repete uma declaração ou grupo de declarações enquanto uma determinada condição for verdadeira. Ele testa a condição antes de executar o corpo do loop. |
| 3 | para loop Como uma instrução while, exceto que testa a condição no final do corpo do loop. |
Declarações de controle de loop
As instruções de controle de loop alteram a execução de sua sequência normal. Quando a execução deixa um escopo, todos os objetos automáticos que foram criados nesse escopo são destruídos.
R suporta as seguintes instruções de controle. Clique nos links a seguir para verificar seus detalhes.
| Sr. Não. | Declaração de controle e descrição |
|---|---|
| 1 | declaração de quebra Termina o loop instrução e transfere a execução para a instrução imediatamente após o loop. |
| 2 | Próxima declaração o next declaração simula o comportamento de R switch. |
Uma função é um conjunto de instruções organizadas em conjunto para realizar uma tarefa específica. R tem um grande número de funções embutidas e o usuário pode criar suas próprias funções.
Em R, uma função é um objeto para que o interpretador de R seja capaz de passar o controle para a função, junto com os argumentos que podem ser necessários para a função realizar as ações.
A função, por sua vez, executa sua tarefa e retorna o controle ao interpretador, bem como qualquer resultado que possa ser armazenado em outros objetos.
Definição de Função
Uma função R é criada usando a palavra-chave function. A sintaxe básica de uma definição de função R é a seguinte -
function_name <- function(arg_1, arg_2, ...) {
Function body
}Componentes de Função
As diferentes partes de uma função são -
Function Name- Este é o nome real da função. Ele é armazenado no ambiente R como um objeto com este nome.
Arguments- Um argumento é um espaço reservado. Quando uma função é chamada, você passa um valor para o argumento. Os argumentos são opcionais; ou seja, uma função não pode conter argumentos. Além disso, os argumentos podem ter valores padrão.
Function Body - O corpo da função contém uma coleção de instruções que definem o que a função faz.
Return Value - O valor de retorno de uma função é a última expressão no corpo da função a ser avaliada.
R tem muitos in-builtfunções que podem ser chamadas diretamente no programa sem defini-las primeiro. Também podemos criar e usar nossas próprias funções, chamadas deuser defined funções.
Função Integrada
Exemplos simples de funções embutidas são seq(), mean(), max(), sum(x) e paste(...)etc. Eles são chamados diretamente por programas escritos pelo usuário. Você pode consultar as funções R mais utilizadas.
# Create a sequence of numbers from 32 to 44.
print(seq(32,44))
# Find mean of numbers from 25 to 82.
print(mean(25:82))
# Find sum of numbers frm 41 to 68.
print(sum(41:68))Quando executamos o código acima, ele produz o seguinte resultado -
[1] 32 33 34 35 36 37 38 39 40 41 42 43 44
[1] 53.5
[1] 1526Função definida pelo usuário
Podemos criar funções definidas pelo usuário em R. Elas são específicas para o que o usuário deseja e, uma vez criadas, podem ser usadas como as funções integradas. Abaixo está um exemplo de como uma função é criada e usada.
# Create a function to print squares of numbers in sequence.
new.function <- function(a) {
for(i in 1:a) {
b <- i^2
print(b)
}
}Chamando uma função
# Create a function to print squares of numbers in sequence.
new.function <- function(a) {
for(i in 1:a) {
b <- i^2
print(b)
}
}
# Call the function new.function supplying 6 as an argument.
new.function(6)Quando executamos o código acima, ele produz o seguinte resultado -
[1] 1
[1] 4
[1] 9
[1] 16
[1] 25
[1] 36Chamando uma função sem um argumento
# Create a function without an argument.
new.function <- function() {
for(i in 1:5) {
print(i^2)
}
}
# Call the function without supplying an argument.
new.function()Quando executamos o código acima, ele produz o seguinte resultado -
[1] 1
[1] 4
[1] 9
[1] 16
[1] 25Chamando uma função com valores de argumento (por posição e por nome)
Os argumentos para uma chamada de função podem ser fornecidos na mesma sequência definida na função ou podem ser fornecidos em uma sequência diferente, mas atribuídos aos nomes dos argumentos.
# Create a function with arguments.
new.function <- function(a,b,c) {
result <- a * b + c
print(result)
}
# Call the function by position of arguments.
new.function(5,3,11)
# Call the function by names of the arguments.
new.function(a = 11, b = 5, c = 3)Quando executamos o código acima, ele produz o seguinte resultado -
[1] 26
[1] 58Chamando uma função com argumento padrão
Podemos definir o valor dos argumentos na definição da função e chamar a função sem fornecer nenhum argumento para obter o resultado padrão. Mas também podemos chamar essas funções fornecendo novos valores do argumento e obter um resultado não padrão.
# Create a function with arguments.
new.function <- function(a = 3, b = 6) {
result <- a * b
print(result)
}
# Call the function without giving any argument.
new.function()
# Call the function with giving new values of the argument.
new.function(9,5)Quando executamos o código acima, ele produz o seguinte resultado -
[1] 18
[1] 45Avaliação Preguiçosa da Função
Argumentos para funções são avaliados lentamente, o que significa que eles são avaliados apenas quando necessário para o corpo da função.
# Create a function with arguments.
new.function <- function(a, b) {
print(a^2)
print(a)
print(b)
}
# Evaluate the function without supplying one of the arguments.
new.function(6)Quando executamos o código acima, ele produz o seguinte resultado -
[1] 36
[1] 6
Error in print(b) : argument "b" is missing, with no defaultQualquer valor escrito em um par de aspas simples ou duplas em R é tratado como uma string. Internamente, R armazena cada string entre aspas duplas, mesmo quando você as cria com aspas simples.
Regras aplicadas na construção de strings
As aspas no início e no final de uma string devem ser aspas duplas ou aspas simples. Eles não podem ser misturados.
As aspas duplas podem ser inseridas em uma string começando e terminando com aspas simples.
As aspas simples podem ser inseridas em uma string começando e terminando com aspas duplas.
As aspas duplas não podem ser inseridas em uma string começando e terminando com aspas duplas.
As aspas simples não podem ser inseridas em uma string começando e terminando com aspas simples.
Exemplos de strings válidas
Os exemplos a seguir esclarecem as regras sobre a criação de uma string em R.
a <- 'Start and end with single quote'
print(a)
b <- "Start and end with double quotes"
print(b)
c <- "single quote ' in between double quotes"
print(c)
d <- 'Double quotes " in between single quote'
print(d)Quando o código acima é executado, obtemos a seguinte saída -
[1] "Start and end with single quote"
[1] "Start and end with double quotes"
[1] "single quote ' in between double quote"
[1] "Double quote \" in between single quote"Exemplos de strings inválidas
e <- 'Mixed quotes"
print(e)
f <- 'Single quote ' inside single quote'
print(f)
g <- "Double quotes " inside double quotes"
print(g)Quando executamos o script, ele falha dando os resultados abaixo.
Error: unexpected symbol in:
"print(e)
f <- 'Single"
Execution haltedManipulação de Cordas
Concatenando Strings - função paste ()
Muitas strings em R são combinadas usando o paste()função. Pode levar qualquer número de argumentos para serem combinados.
Sintaxe
A sintaxe básica para a função colar é -
paste(..., sep = " ", collapse = NULL)A seguir está a descrição dos parâmetros usados -
... representa qualquer número de argumentos a serem combinados.
seprepresenta qualquer separador entre os argumentos. Isso é opcional.
collapseé usado para eliminar o espaço entre duas strings. Mas não o espaço dentro de duas palavras de uma string.
Exemplo
a <- "Hello"
b <- 'How'
c <- "are you? "
print(paste(a,b,c))
print(paste(a,b,c, sep = "-"))
print(paste(a,b,c, sep = "", collapse = ""))Quando executamos o código acima, ele produz o seguinte resultado -
[1] "Hello How are you? "
[1] "Hello-How-are you? "
[1] "HelloHoware you? "Formatando números e strings - função format ()
Números e strings podem ser formatados para um estilo específico usando format() função.
Sintaxe
A sintaxe básica para a função de formato é -
format(x, digits, nsmall, scientific, width, justify = c("left", "right", "centre", "none"))A seguir está a descrição dos parâmetros usados -
x é a entrada do vetor.
digits é o número total de dígitos exibidos.
nsmall é o número mínimo de dígitos à direita da vírgula decimal.
scientific é definido como TRUE para exibir notação científica.
width indica a largura mínima a ser exibida preenchendo espaços em branco no início.
justify é a exibição da corda à esquerda, direita ou centro.
Exemplo
# Total number of digits displayed. Last digit rounded off.
result <- format(23.123456789, digits = 9)
print(result)
# Display numbers in scientific notation.
result <- format(c(6, 13.14521), scientific = TRUE)
print(result)
# The minimum number of digits to the right of the decimal point.
result <- format(23.47, nsmall = 5)
print(result)
# Format treats everything as a string.
result <- format(6)
print(result)
# Numbers are padded with blank in the beginning for width.
result <- format(13.7, width = 6)
print(result)
# Left justify strings.
result <- format("Hello", width = 8, justify = "l")
print(result)
# Justfy string with center.
result <- format("Hello", width = 8, justify = "c")
print(result)Quando executamos o código acima, ele produz o seguinte resultado -
[1] "23.1234568"
[1] "6.000000e+00" "1.314521e+01"
[1] "23.47000"
[1] "6"
[1] " 13.7"
[1] "Hello "
[1] " Hello "Contando o número de caracteres em uma string - função nchar ()
Esta função conta o número de caracteres, incluindo espaços em uma string.
Sintaxe
A sintaxe básica para a função nchar () é -
nchar(x)A seguir está a descrição dos parâmetros usados -
x é a entrada do vetor.
Exemplo
result <- nchar("Count the number of characters")
print(result)Quando executamos o código acima, ele produz o seguinte resultado -
[1] 30Alterando o caso - funções toupper () e tolower ()
Essas funções alteram a capitalização dos caracteres de uma string.
Sintaxe
A sintaxe básica para a função toupper () & tolower () é -
toupper(x)
tolower(x)A seguir está a descrição dos parâmetros usados -
x é a entrada do vetor.
Exemplo
# Changing to Upper case.
result <- toupper("Changing To Upper")
print(result)
# Changing to lower case.
result <- tolower("Changing To Lower")
print(result)Quando executamos o código acima, ele produz o seguinte resultado -
[1] "CHANGING TO UPPER"
[1] "changing to lower"Extraindo partes de uma função string - substring ()
Esta função extrai partes de uma String.
Sintaxe
A sintaxe básica para a função substring () é -
substring(x,first,last)A seguir está a descrição dos parâmetros usados -
x é a entrada do vetor de caracteres.
first é a posição do primeiro caractere a ser extraído.
last é a posição do último caractere a ser extraído.
Exemplo
# Extract characters from 5th to 7th position.
result <- substring("Extract", 5, 7)
print(result)Quando executamos o código acima, ele produz o seguinte resultado -
[1] "act"Vetores são os objetos de dados R mais básicos e existem seis tipos de vetores atômicos. Eles são lógicos, inteiros, duplos, complexos, de caráter e brutos.
Criação de Vetor
Vetor de elemento único
Mesmo quando você escreve apenas um valor em R, ele se torna um vetor de comprimento 1 e pertence a um dos tipos de vetor acima.
# Atomic vector of type character.
print("abc");
# Atomic vector of type double.
print(12.5)
# Atomic vector of type integer.
print(63L)
# Atomic vector of type logical.
print(TRUE)
# Atomic vector of type complex.
print(2+3i)
# Atomic vector of type raw.
print(charToRaw('hello'))Quando executamos o código acima, ele produz o seguinte resultado -
[1] "abc"
[1] 12.5
[1] 63
[1] TRUE
[1] 2+3i
[1] 68 65 6c 6c 6fVetor de vários elementos
Using colon operator with numeric data
# Creating a sequence from 5 to 13.
v <- 5:13
print(v)
# Creating a sequence from 6.6 to 12.6.
v <- 6.6:12.6
print(v)
# If the final element specified does not belong to the sequence then it is discarded.
v <- 3.8:11.4
print(v)Quando executamos o código acima, ele produz o seguinte resultado -
[1] 5 6 7 8 9 10 11 12 13
[1] 6.6 7.6 8.6 9.6 10.6 11.6 12.6
[1] 3.8 4.8 5.8 6.8 7.8 8.8 9.8 10.8Using sequence (Seq.) operator
# Create vector with elements from 5 to 9 incrementing by 0.4.
print(seq(5, 9, by = 0.4))Quando executamos o código acima, ele produz o seguinte resultado -
[1] 5.0 5.4 5.8 6.2 6.6 7.0 7.4 7.8 8.2 8.6 9.0Using the c() function
Os valores que não são caracteres são forçados ao tipo de caractere se um dos elementos for um caractere.
# The logical and numeric values are converted to characters.
s <- c('apple','red',5,TRUE)
print(s)Quando executamos o código acima, ele produz o seguinte resultado -
[1] "apple" "red" "5" "TRUE"Acessando Elementos do Vetor
Os elementos de um vetor são acessados por meio de indexação. o[ ] bracketssão usados para indexação. A indexação começa com a posição 1. Dar um valor negativo no índice remove esse elemento do resultado.TRUE, FALSE ou 0 e 1 também pode ser usado para indexação.
# Accessing vector elements using position.
t <- c("Sun","Mon","Tue","Wed","Thurs","Fri","Sat")
u <- t[c(2,3,6)]
print(u)
# Accessing vector elements using logical indexing.
v <- t[c(TRUE,FALSE,FALSE,FALSE,FALSE,TRUE,FALSE)]
print(v)
# Accessing vector elements using negative indexing.
x <- t[c(-2,-5)]
print(x)
# Accessing vector elements using 0/1 indexing.
y <- t[c(0,0,0,0,0,0,1)]
print(y)Quando executamos o código acima, ele produz o seguinte resultado -
[1] "Mon" "Tue" "Fri"
[1] "Sun" "Fri"
[1] "Sun" "Tue" "Wed" "Fri" "Sat"
[1] "Sun"Manipulação de Vetor
Aritmética vetorial
Dois vetores de mesmo comprimento podem ser adicionados, subtraídos, multiplicados ou divididos, dando o resultado como uma saída de vetor.
# Create two vectors.
v1 <- c(3,8,4,5,0,11)
v2 <- c(4,11,0,8,1,2)
# Vector addition.
add.result <- v1+v2
print(add.result)
# Vector subtraction.
sub.result <- v1-v2
print(sub.result)
# Vector multiplication.
multi.result <- v1*v2
print(multi.result)
# Vector division.
divi.result <- v1/v2
print(divi.result)Quando executamos o código acima, ele produz o seguinte resultado -
[1] 7 19 4 13 1 13
[1] -1 -3 4 -3 -1 9
[1] 12 88 0 40 0 22
[1] 0.7500000 0.7272727 Inf 0.6250000 0.0000000 5.5000000Reciclagem de elemento vetorial
Se aplicarmos operações aritméticas a dois vetores de comprimento desigual, os elementos do vetor mais curto serão reciclados para completar as operações.
v1 <- c(3,8,4,5,0,11)
v2 <- c(4,11)
# V2 becomes c(4,11,4,11,4,11)
add.result <- v1+v2
print(add.result)
sub.result <- v1-v2
print(sub.result)Quando executamos o código acima, ele produz o seguinte resultado -
[1] 7 19 8 16 4 22
[1] -1 -3 0 -6 -4 0Classificação de elemento vetorial
Os elementos em um vetor podem ser classificados usando o sort() função.
v <- c(3,8,4,5,0,11, -9, 304)
# Sort the elements of the vector.
sort.result <- sort(v)
print(sort.result)
# Sort the elements in the reverse order.
revsort.result <- sort(v, decreasing = TRUE)
print(revsort.result)
# Sorting character vectors.
v <- c("Red","Blue","yellow","violet")
sort.result <- sort(v)
print(sort.result)
# Sorting character vectors in reverse order.
revsort.result <- sort(v, decreasing = TRUE)
print(revsort.result)Quando executamos o código acima, ele produz o seguinte resultado -
[1] -9 0 3 4 5 8 11 304
[1] 304 11 8 5 4 3 0 -9
[1] "Blue" "Red" "violet" "yellow"
[1] "yellow" "violet" "Red" "Blue"Listas são os objetos R que contêm elementos de diferentes tipos como - números, strings, vetores e outra lista dentro deles. Uma lista também pode conter uma matriz ou uma função como seus elementos. A lista é criada usandolist() função.
Criação de uma lista
A seguir está um exemplo para criar uma lista contendo strings, números, vetores e valores lógicos.
# Create a list containing strings, numbers, vectors and a logical
# values.
list_data <- list("Red", "Green", c(21,32,11), TRUE, 51.23, 119.1)
print(list_data)Quando executamos o código acima, ele produz o seguinte resultado -
[[1]]
[1] "Red"
[[2]]
[1] "Green"
[[3]]
[1] 21 32 11
[[4]]
[1] TRUE
[[5]]
[1] 51.23
[[6]]
[1] 119.1Elementos da lista de nomes
Os elementos da lista podem receber nomes e eles podem ser acessados usando esses nomes.
# Create a list containing a vector, a matrix and a list.
list_data <- list(c("Jan","Feb","Mar"), matrix(c(3,9,5,1,-2,8), nrow = 2),
list("green",12.3))
# Give names to the elements in the list.
names(list_data) <- c("1st Quarter", "A_Matrix", "A Inner list")
# Show the list.
print(list_data)Quando executamos o código acima, ele produz o seguinte resultado -
$`1st_Quarter` [1] "Jan" "Feb" "Mar" $A_Matrix
[,1] [,2] [,3]
[1,] 3 5 -2
[2,] 9 1 8
$A_Inner_list $A_Inner_list[[1]]
[1] "green"
$A_Inner_list[[2]]
[1] 12.3Acessando Elementos da Lista
Os elementos da lista podem ser acessados pelo índice do elemento na lista. No caso de listas nomeadas, também pode ser acessado usando os nomes.
Continuamos a usar a lista no exemplo acima -
# Create a list containing a vector, a matrix and a list.
list_data <- list(c("Jan","Feb","Mar"), matrix(c(3,9,5,1,-2,8), nrow = 2),
list("green",12.3))
# Give names to the elements in the list.
names(list_data) <- c("1st Quarter", "A_Matrix", "A Inner list")
# Access the first element of the list.
print(list_data[1])
# Access the thrid element. As it is also a list, all its elements will be printed.
print(list_data[3])
# Access the list element using the name of the element.
print(list_data$A_Matrix)Quando executamos o código acima, ele produz o seguinte resultado -
$`1st_Quarter` [1] "Jan" "Feb" "Mar" $A_Inner_list
$A_Inner_list[[1]] [1] "green" $A_Inner_list[[2]]
[1] 12.3
[,1] [,2] [,3]
[1,] 3 5 -2
[2,] 9 1 8Manipulando Elementos de Lista
Podemos adicionar, excluir e atualizar os elementos da lista conforme mostrado abaixo. Podemos adicionar e excluir elementos apenas no final de uma lista. Mas podemos atualizar qualquer elemento.
# Create a list containing a vector, a matrix and a list.
list_data <- list(c("Jan","Feb","Mar"), matrix(c(3,9,5,1,-2,8), nrow = 2),
list("green",12.3))
# Give names to the elements in the list.
names(list_data) <- c("1st Quarter", "A_Matrix", "A Inner list")
# Add element at the end of the list.
list_data[4] <- "New element"
print(list_data[4])
# Remove the last element.
list_data[4] <- NULL
# Print the 4th Element.
print(list_data[4])
# Update the 3rd Element.
list_data[3] <- "updated element"
print(list_data[3])Quando executamos o código acima, ele produz o seguinte resultado -
[[1]]
[1] "New element"
$<NA> NULL $`A Inner list`
[1] "updated element"Mesclando Listas
Você pode mesclar muitas listas em uma lista, colocando todas as listas dentro de uma função list ().
# Create two lists.
list1 <- list(1,2,3)
list2 <- list("Sun","Mon","Tue")
# Merge the two lists.
merged.list <- c(list1,list2)
# Print the merged list.
print(merged.list)Quando executamos o código acima, ele produz o seguinte resultado -
[[1]]
[1] 1
[[2]]
[1] 2
[[3]]
[1] 3
[[4]]
[1] "Sun"
[[5]]
[1] "Mon"
[[6]]
[1] "Tue"Convertendo lista em vetor
Uma lista pode ser convertida em um vetor para que os elementos do vetor possam ser usados para manipulação posterior. Todas as operações aritméticas em vetores podem ser aplicadas após a lista ser convertida em vetores. Para fazer essa conversão, usamos ounlist()função. Ele pega a lista como entrada e produz um vetor.
# Create lists.
list1 <- list(1:5)
print(list1)
list2 <-list(10:14)
print(list2)
# Convert the lists to vectors.
v1 <- unlist(list1)
v2 <- unlist(list2)
print(v1)
print(v2)
# Now add the vectors
result <- v1+v2
print(result)Quando executamos o código acima, ele produz o seguinte resultado -
[[1]]
[1] 1 2 3 4 5
[[1]]
[1] 10 11 12 13 14
[1] 1 2 3 4 5
[1] 10 11 12 13 14
[1] 11 13 15 17 19Matrizes são os objetos R nos quais os elementos são organizados em um layout retangular bidimensional. Eles contêm elementos dos mesmos tipos atômicos. Embora possamos criar uma matriz contendo apenas caracteres ou apenas valores lógicos, eles não têm muita utilidade. Usamos matrizes contendo elementos numéricos para serem usadas em cálculos matemáticos.
Uma matriz é criada usando o matrix() função.
Sintaxe
A sintaxe básica para criar uma matriz em R é -
matrix(data, nrow, ncol, byrow, dimnames)A seguir está a descrição dos parâmetros usados -
data é o vetor de entrada que se torna os elementos de dados da matriz.
nrow é o número de linhas a serem criadas.
ncol é o número de colunas a serem criadas.
byrowé uma pista lógica. Se TRUE, os elementos do vetor de entrada são organizados por linha.
dimname são os nomes atribuídos às linhas e colunas.
Exemplo
Crie uma matriz tendo um vetor de números como entrada.
# Elements are arranged sequentially by row.
M <- matrix(c(3:14), nrow = 4, byrow = TRUE)
print(M)
# Elements are arranged sequentially by column.
N <- matrix(c(3:14), nrow = 4, byrow = FALSE)
print(N)
# Define the column and row names.
rownames = c("row1", "row2", "row3", "row4")
colnames = c("col1", "col2", "col3")
P <- matrix(c(3:14), nrow = 4, byrow = TRUE, dimnames = list(rownames, colnames))
print(P)Quando executamos o código acima, ele produz o seguinte resultado -
[,1] [,2] [,3]
[1,] 3 4 5
[2,] 6 7 8
[3,] 9 10 11
[4,] 12 13 14
[,1] [,2] [,3]
[1,] 3 7 11
[2,] 4 8 12
[3,] 5 9 13
[4,] 6 10 14
col1 col2 col3
row1 3 4 5
row2 6 7 8
row3 9 10 11
row4 12 13 14Acessando Elementos de uma Matriz
Os elementos de uma matriz podem ser acessados usando o índice de coluna e linha do elemento. Consideramos a matriz P acima para encontrar os elementos específicos abaixo.
# Define the column and row names.
rownames = c("row1", "row2", "row3", "row4")
colnames = c("col1", "col2", "col3")
# Create the matrix.
P <- matrix(c(3:14), nrow = 4, byrow = TRUE, dimnames = list(rownames, colnames))
# Access the element at 3rd column and 1st row.
print(P[1,3])
# Access the element at 2nd column and 4th row.
print(P[4,2])
# Access only the 2nd row.
print(P[2,])
# Access only the 3rd column.
print(P[,3])Quando executamos o código acima, ele produz o seguinte resultado -
[1] 5
[1] 13
col1 col2 col3
6 7 8
row1 row2 row3 row4
5 8 11 14Computações Matrix
Várias operações matemáticas são realizadas nas matrizes usando os operadores R. O resultado da operação também é uma matriz.
As dimensões (número de linhas e colunas) devem ser as mesmas para as matrizes envolvidas na operação.
Adição e subtração de matriz
# Create two 2x3 matrices.
matrix1 <- matrix(c(3, 9, -1, 4, 2, 6), nrow = 2)
print(matrix1)
matrix2 <- matrix(c(5, 2, 0, 9, 3, 4), nrow = 2)
print(matrix2)
# Add the matrices.
result <- matrix1 + matrix2
cat("Result of addition","\n")
print(result)
# Subtract the matrices
result <- matrix1 - matrix2
cat("Result of subtraction","\n")
print(result)Quando executamos o código acima, ele produz o seguinte resultado -
[,1] [,2] [,3]
[1,] 3 -1 2
[2,] 9 4 6
[,1] [,2] [,3]
[1,] 5 0 3
[2,] 2 9 4
Result of addition
[,1] [,2] [,3]
[1,] 8 -1 5
[2,] 11 13 10
Result of subtraction
[,1] [,2] [,3]
[1,] -2 -1 -1
[2,] 7 -5 2Multiplicação e divisão de matriz
# Create two 2x3 matrices.
matrix1 <- matrix(c(3, 9, -1, 4, 2, 6), nrow = 2)
print(matrix1)
matrix2 <- matrix(c(5, 2, 0, 9, 3, 4), nrow = 2)
print(matrix2)
# Multiply the matrices.
result <- matrix1 * matrix2
cat("Result of multiplication","\n")
print(result)
# Divide the matrices
result <- matrix1 / matrix2
cat("Result of division","\n")
print(result)Quando executamos o código acima, ele produz o seguinte resultado -
[,1] [,2] [,3]
[1,] 3 -1 2
[2,] 9 4 6
[,1] [,2] [,3]
[1,] 5 0 3
[2,] 2 9 4
Result of multiplication
[,1] [,2] [,3]
[1,] 15 0 6
[2,] 18 36 24
Result of division
[,1] [,2] [,3]
[1,] 0.6 -Inf 0.6666667
[2,] 4.5 0.4444444 1.5000000Arrays são objetos de dados R que podem armazenar dados em mais de duas dimensões. Por exemplo - Se criarmos uma matriz de dimensão (2, 3, 4), então ele cria 4 matrizes retangulares, cada uma com 2 linhas e 3 colunas. Os arrays podem armazenar apenas o tipo de dados.
Uma matriz é criada usando o array()função. Ele pega vetores como entrada e usa os valores nodim parâmetro para criar uma matriz.
Exemplo
O exemplo a seguir cria uma matriz de duas matrizes 3x3, cada uma com 3 linhas e 3 colunas.
# Create two vectors of different lengths.
vector1 <- c(5,9,3)
vector2 <- c(10,11,12,13,14,15)
# Take these vectors as input to the array.
result <- array(c(vector1,vector2),dim = c(3,3,2))
print(result)Quando executamos o código acima, ele produz o seguinte resultado -
, , 1
[,1] [,2] [,3]
[1,] 5 10 13
[2,] 9 11 14
[3,] 3 12 15
, , 2
[,1] [,2] [,3]
[1,] 5 10 13
[2,] 9 11 14
[3,] 3 12 15Nomeando colunas e linhas
Podemos dar nomes às linhas, colunas e matrizes da matriz usando o dimnames parâmetro.
# Create two vectors of different lengths.
vector1 <- c(5,9,3)
vector2 <- c(10,11,12,13,14,15)
column.names <- c("COL1","COL2","COL3")
row.names <- c("ROW1","ROW2","ROW3")
matrix.names <- c("Matrix1","Matrix2")
# Take these vectors as input to the array.
result <- array(c(vector1,vector2),dim = c(3,3,2),dimnames = list(row.names,column.names,
matrix.names))
print(result)Quando executamos o código acima, ele produz o seguinte resultado -
, , Matrix1
COL1 COL2 COL3
ROW1 5 10 13
ROW2 9 11 14
ROW3 3 12 15
, , Matrix2
COL1 COL2 COL3
ROW1 5 10 13
ROW2 9 11 14
ROW3 3 12 15Acessando Elementos de Matriz
# Create two vectors of different lengths.
vector1 <- c(5,9,3)
vector2 <- c(10,11,12,13,14,15)
column.names <- c("COL1","COL2","COL3")
row.names <- c("ROW1","ROW2","ROW3")
matrix.names <- c("Matrix1","Matrix2")
# Take these vectors as input to the array.
result <- array(c(vector1,vector2),dim = c(3,3,2),dimnames = list(row.names,
column.names, matrix.names))
# Print the third row of the second matrix of the array.
print(result[3,,2])
# Print the element in the 1st row and 3rd column of the 1st matrix.
print(result[1,3,1])
# Print the 2nd Matrix.
print(result[,,2])Quando executamos o código acima, ele produz o seguinte resultado -
COL1 COL2 COL3
3 12 15
[1] 13
COL1 COL2 COL3
ROW1 5 10 13
ROW2 9 11 14
ROW3 3 12 15Manipulando Elementos de Matriz
Como a matriz é composta por matrizes em múltiplas dimensões, as operações nos elementos da matriz são realizadas acessando os elementos das matrizes.
# Create two vectors of different lengths.
vector1 <- c(5,9,3)
vector2 <- c(10,11,12,13,14,15)
# Take these vectors as input to the array.
array1 <- array(c(vector1,vector2),dim = c(3,3,2))
# Create two vectors of different lengths.
vector3 <- c(9,1,0)
vector4 <- c(6,0,11,3,14,1,2,6,9)
array2 <- array(c(vector1,vector2),dim = c(3,3,2))
# create matrices from these arrays.
matrix1 <- array1[,,2]
matrix2 <- array2[,,2]
# Add the matrices.
result <- matrix1+matrix2
print(result)Quando executamos o código acima, ele produz o seguinte resultado -
[,1] [,2] [,3]
[1,] 10 20 26
[2,] 18 22 28
[3,] 6 24 30Cálculos entre os elementos da matriz
Podemos fazer cálculos entre os elementos em uma matriz usando o apply() função.
Sintaxe
apply(x, margin, fun)A seguir está a descrição dos parâmetros usados -
x é uma matriz.
margin é o nome do conjunto de dados usado.
fun é a função a ser aplicada aos elementos da matriz.
Exemplo
Usamos a função apply () abaixo para calcular a soma dos elementos nas linhas de uma matriz em todas as matrizes.
# Create two vectors of different lengths.
vector1 <- c(5,9,3)
vector2 <- c(10,11,12,13,14,15)
# Take these vectors as input to the array.
new.array <- array(c(vector1,vector2),dim = c(3,3,2))
print(new.array)
# Use apply to calculate the sum of the rows across all the matrices.
result <- apply(new.array, c(1), sum)
print(result)Quando executamos o código acima, ele produz o seguinte resultado -
, , 1
[,1] [,2] [,3]
[1,] 5 10 13
[2,] 9 11 14
[3,] 3 12 15
, , 2
[,1] [,2] [,3]
[1,] 5 10 13
[2,] 9 11 14
[3,] 3 12 15
[1] 56 68 60Fatores são os objetos de dados usados para categorizar os dados e armazená-los como níveis. Eles podem armazenar strings e inteiros. Eles são úteis nas colunas que possuem um número limitado de valores únicos. Como "Masculino," Feminino "e Verdadeiro, Falso etc. Eles são úteis na análise de dados para modelagem estatística.
Fatores são criados usando o factor () função tomando um vetor como entrada.
Exemplo
# Create a vector as input.
data <- c("East","West","East","North","North","East","West","West","West","East","North")
print(data)
print(is.factor(data))
# Apply the factor function.
factor_data <- factor(data)
print(factor_data)
print(is.factor(factor_data))Quando executamos o código acima, ele produz o seguinte resultado -
[1] "East" "West" "East" "North" "North" "East" "West" "West" "West" "East" "North"
[1] FALSE
[1] East West East North North East West West West East North
Levels: East North West
[1] TRUEFatores no quadro de dados
Ao criar qualquer quadro de dados com uma coluna de dados de texto, R trata a coluna de texto como dados categóricos e cria fatores sobre ela.
# Create the vectors for data frame.
height <- c(132,151,162,139,166,147,122)
weight <- c(48,49,66,53,67,52,40)
gender <- c("male","male","female","female","male","female","male")
# Create the data frame.
input_data <- data.frame(height,weight,gender)
print(input_data)
# Test if the gender column is a factor.
print(is.factor(input_data$gender)) # Print the gender column so see the levels. print(input_data$gender)Quando executamos o código acima, ele produz o seguinte resultado -
height weight gender
1 132 48 male
2 151 49 male
3 162 66 female
4 139 53 female
5 166 67 male
6 147 52 female
7 122 40 male
[1] TRUE
[1] male male female female male female male
Levels: female maleMudando a ordem dos níveis
A ordem dos níveis em um fator pode ser alterada aplicando a função de fator novamente com a nova ordem dos níveis.
data <- c("East","West","East","North","North","East","West",
"West","West","East","North")
# Create the factors
factor_data <- factor(data)
print(factor_data)
# Apply the factor function with required order of the level.
new_order_data <- factor(factor_data,levels = c("East","West","North"))
print(new_order_data)Quando executamos o código acima, ele produz o seguinte resultado -
[1] East West East North North East West West West East North
Levels: East North West
[1] East West East North North East West West West East North
Levels: East West NorthNíveis de fator de geração
Podemos gerar níveis de fator usando o gl()função. Leva dois inteiros como entrada que indicam quantos níveis e quantas vezes cada nível.
Sintaxe
gl(n, k, labels)A seguir está a descrição dos parâmetros usados -
n é um número inteiro que fornece o número de níveis.
k é um número inteiro que fornece o número de replicações.
labels é um vetor de rótulos para os níveis de fator resultantes.
Exemplo
v <- gl(3, 4, labels = c("Tampa", "Seattle","Boston"))
print(v)Quando executamos o código acima, ele produz o seguinte resultado -
Tampa Tampa Tampa Tampa Seattle Seattle Seattle Seattle Boston
[10] Boston Boston Boston
Levels: Tampa Seattle BostonUm quadro de dados é uma tabela ou uma estrutura semelhante a uma matriz bidimensional em que cada coluna contém valores de uma variável e cada linha contém um conjunto de valores de cada coluna.
A seguir estão as características de um quadro de dados.
- Os nomes das colunas não devem estar vazios.
- Os nomes das linhas devem ser exclusivos.
- Os dados armazenados em um quadro de dados podem ser numéricos, fator ou tipo de caractere.
- Cada coluna deve conter o mesmo número de itens de dados.
Criar quadro de dados
# Create the data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01", "2013-09-23", "2014-11-15", "2014-05-11",
"2015-03-27")),
stringsAsFactors = FALSE
)
# Print the data frame.
print(emp.data)Quando executamos o código acima, ele produz o seguinte resultado -
emp_id emp_name salary start_date
1 1 Rick 623.30 2012-01-01
2 2 Dan 515.20 2013-09-23
3 3 Michelle 611.00 2014-11-15
4 4 Ryan 729.00 2014-05-11
5 5 Gary 843.25 2015-03-27Obtenha a estrutura do quadro de dados
A estrutura do quadro de dados pode ser vista usando str() função.
# Create the data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01", "2013-09-23", "2014-11-15", "2014-05-11",
"2015-03-27")),
stringsAsFactors = FALSE
)
# Get the structure of the data frame.
str(emp.data)Quando executamos o código acima, ele produz o seguinte resultado -
'data.frame': 5 obs. of 4 variables:
$ emp_id : int 1 2 3 4 5 $ emp_name : chr "Rick" "Dan" "Michelle" "Ryan" ...
$ salary : num 623 515 611 729 843 $ start_date: Date, format: "2012-01-01" "2013-09-23" "2014-11-15" "2014-05-11" ...Resumo dos dados no quadro de dados
O resumo estatístico e a natureza dos dados podem ser obtidos aplicando summary() função.
# Create the data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01", "2013-09-23", "2014-11-15", "2014-05-11",
"2015-03-27")),
stringsAsFactors = FALSE
)
# Print the summary.
print(summary(emp.data))Quando executamos o código acima, ele produz o seguinte resultado -
emp_id emp_name salary start_date
Min. :1 Length:5 Min. :515.2 Min. :2012-01-01
1st Qu.:2 Class :character 1st Qu.:611.0 1st Qu.:2013-09-23
Median :3 Mode :character Median :623.3 Median :2014-05-11
Mean :3 Mean :664.4 Mean :2014-01-14
3rd Qu.:4 3rd Qu.:729.0 3rd Qu.:2014-11-15
Max. :5 Max. :843.2 Max. :2015-03-27Extraia dados do quadro de dados
Extraia uma coluna específica de um quadro de dados usando o nome da coluna.
# Create the data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01","2013-09-23","2014-11-15","2014-05-11",
"2015-03-27")),
stringsAsFactors = FALSE
)
# Extract Specific columns.
result <- data.frame(emp.data$emp_name,emp.data$salary)
print(result)Quando executamos o código acima, ele produz o seguinte resultado -
emp.data.emp_name emp.data.salary
1 Rick 623.30
2 Dan 515.20
3 Michelle 611.00
4 Ryan 729.00
5 Gary 843.25Extraia as duas primeiras linhas e depois todas as colunas
# Create the data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01", "2013-09-23", "2014-11-15", "2014-05-11",
"2015-03-27")),
stringsAsFactors = FALSE
)
# Extract first two rows.
result <- emp.data[1:2,]
print(result)Quando executamos o código acima, ele produz o seguinte resultado -
emp_id emp_name salary start_date
1 1 Rick 623.3 2012-01-01
2 2 Dan 515.2 2013-09-23Extrair 3 rd e 5 th linha com 2 nd e 4 th coluna
# Create the data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01", "2013-09-23", "2014-11-15", "2014-05-11",
"2015-03-27")),
stringsAsFactors = FALSE
)
# Extract 3rd and 5th row with 2nd and 4th column.
result <- emp.data[c(3,5),c(2,4)]
print(result)Quando executamos o código acima, ele produz o seguinte resultado -
emp_name start_date
3 Michelle 2014-11-15
5 Gary 2015-03-27Expandir Quadro de Dados
Um quadro de dados pode ser expandido adicionando colunas e linhas.
Adicionar coluna
Basta adicionar o vetor da coluna usando um novo nome de coluna.
# Create the data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01", "2013-09-23", "2014-11-15", "2014-05-11",
"2015-03-27")),
stringsAsFactors = FALSE
)
# Add the "dept" coulmn.
emp.data$dept <- c("IT","Operations","IT","HR","Finance")
v <- emp.data
print(v)Quando executamos o código acima, ele produz o seguinte resultado -
emp_id emp_name salary start_date dept
1 1 Rick 623.30 2012-01-01 IT
2 2 Dan 515.20 2013-09-23 Operations
3 3 Michelle 611.00 2014-11-15 IT
4 4 Ryan 729.00 2014-05-11 HR
5 5 Gary 843.25 2015-03-27 FinanceAdicionar linha
Para adicionar mais linhas permanentemente a um quadro de dados existente, precisamos trazer as novas linhas na mesma estrutura do quadro de dados existente e usar o rbind() função.
No exemplo abaixo, criamos um quadro de dados com novas linhas e o fundimos com o quadro de dados existente para criar o quadro de dados final.
# Create the first data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01", "2013-09-23", "2014-11-15", "2014-05-11",
"2015-03-27")),
dept = c("IT","Operations","IT","HR","Finance"),
stringsAsFactors = FALSE
)
# Create the second data frame
emp.newdata <- data.frame(
emp_id = c (6:8),
emp_name = c("Rasmi","Pranab","Tusar"),
salary = c(578.0,722.5,632.8),
start_date = as.Date(c("2013-05-21","2013-07-30","2014-06-17")),
dept = c("IT","Operations","Fianance"),
stringsAsFactors = FALSE
)
# Bind the two data frames.
emp.finaldata <- rbind(emp.data,emp.newdata)
print(emp.finaldata)Quando executamos o código acima, ele produz o seguinte resultado -
emp_id emp_name salary start_date dept
1 1 Rick 623.30 2012-01-01 IT
2 2 Dan 515.20 2013-09-23 Operations
3 3 Michelle 611.00 2014-11-15 IT
4 4 Ryan 729.00 2014-05-11 HR
5 5 Gary 843.25 2015-03-27 Finance
6 6 Rasmi 578.00 2013-05-21 IT
7 7 Pranab 722.50 2013-07-30 Operations
8 8 Tusar 632.80 2014-06-17 FiananceOs pacotes R são uma coleção de funções R, código compilado e dados de amostra. Eles são armazenados em um diretório chamado"library"no ambiente R. Por padrão, R instala um conjunto de pacotes durante a instalação. Mais pacotes são adicionados posteriormente, quando são necessários para algum propósito específico. Quando iniciamos o console R, apenas os pacotes padrão estão disponíveis por padrão. Outros pacotes que já estão instalados devem ser carregados explicitamente para serem usados pelo programa R que irá usá-los.
Todos os pacotes disponíveis na linguagem R estão listados em Pacotes R.
Abaixo está uma lista de comandos a serem usados para verificar, verificar e usar os pacotes R.
Verifique os pacotes R disponíveis
Obtenha localizações de bibliotecas contendo pacotes R
.libPaths()Quando executamos o código acima, ele produz o seguinte resultado. Isso pode variar dependendo das configurações locais do seu PC.
[2] "C:/Program Files/R/R-3.2.2/library"Obtenha a lista de todos os pacotes instalados
library()Quando executamos o código acima, ele produz o seguinte resultado. Isso pode variar dependendo das configurações locais do seu PC.
Packages in library ‘C:/Program Files/R/R-3.2.2/library’:
base The R Base Package
boot Bootstrap Functions (Originally by Angelo Canty
for S)
class Functions for Classification
cluster "Finding Groups in Data": Cluster Analysis
Extended Rousseeuw et al.
codetools Code Analysis Tools for R
compiler The R Compiler Package
datasets The R Datasets Package
foreign Read Data Stored by 'Minitab', 'S', 'SAS',
'SPSS', 'Stata', 'Systat', 'Weka', 'dBase', ...
graphics The R Graphics Package
grDevices The R Graphics Devices and Support for Colours
and Fonts
grid The Grid Graphics Package
KernSmooth Functions for Kernel Smoothing Supporting Wand
& Jones (1995)
lattice Trellis Graphics for R
MASS Support Functions and Datasets for Venables and
Ripley's MASS
Matrix Sparse and Dense Matrix Classes and Methods
methods Formal Methods and Classes
mgcv Mixed GAM Computation Vehicle with GCV/AIC/REML
Smoothness Estimation
nlme Linear and Nonlinear Mixed Effects Models
nnet Feed-Forward Neural Networks and Multinomial
Log-Linear Models
parallel Support for Parallel computation in R
rpart Recursive Partitioning and Regression Trees
spatial Functions for Kriging and Point Pattern
Analysis
splines Regression Spline Functions and Classes
stats The R Stats Package
stats4 Statistical Functions using S4 Classes
survival Survival Analysis
tcltk Tcl/Tk Interface
tools Tools for Package Development
utils The R Utils PackageObtenha todos os pacotes carregados atualmente no ambiente R
search()Quando executamos o código acima, ele produz o seguinte resultado. Isso pode variar dependendo das configurações locais do seu PC.
[1] ".GlobalEnv" "package:stats" "package:graphics"
[4] "package:grDevices" "package:utils" "package:datasets"
[7] "package:methods" "Autoloads" "package:base"Instale um novo pacote
Existem duas maneiras de adicionar novos pacotes R. Um é instalar diretamente do diretório CRAN e outro é baixar o pacote para seu sistema local e instalá-lo manualmente.
Instale diretamente do CRAN
O comando a seguir obtém os pacotes diretamente da página da Web do CRAN e instala o pacote no ambiente R. Você pode ser solicitado a escolher um espelho mais próximo. Escolha o apropriado para sua localização.
install.packages("Package Name")
# Install the package named "XML".
install.packages("XML")Instale o pacote manualmente
Acesse o link Pacotes R para baixar o pacote necessário. Salve o pacote como um.zip arquivo em um local adequado no sistema local.
Agora você pode executar o seguinte comando para instalar este pacote no ambiente R.
install.packages(file_name_with_path, repos = NULL, type = "source")
# Install the package named "XML"
install.packages("E:/XML_3.98-1.3.zip", repos = NULL, type = "source")Carregar pacote na biblioteca
Antes que um pacote possa ser usado no código, ele deve ser carregado no ambiente R atual. Você também precisa carregar um pacote que já está instalado anteriormente, mas não disponível no ambiente atual.
Um pacote é carregado usando o seguinte comando -
library("package Name", lib.loc = "path to library")
# Load the package named "XML"
install.packages("E:/XML_3.98-1.3.zip", repos = NULL, type = "source")A remodelagem de dados em R trata de alterar a maneira como os dados são organizados em linhas e colunas. Na maior parte do tempo, o processamento de dados em R é feito tomando os dados de entrada como um quadro de dados. É fácil extrair dados das linhas e colunas de um quadro de dados, mas há situações em que precisamos do quadro de dados em um formato diferente do formato em que o recebemos. R tem muitas funções para dividir, mesclar e transformar as linhas em colunas e vice-versa em um quadro de dados.
Juntando colunas e linhas em um quadro de dados
Podemos juntar vários vetores para criar um quadro de dados usando o cbind()função. Também podemos fundir dois quadros de dados usandorbind() função.
# Create vector objects.
city <- c("Tampa","Seattle","Hartford","Denver")
state <- c("FL","WA","CT","CO")
zipcode <- c(33602,98104,06161,80294)
# Combine above three vectors into one data frame.
addresses <- cbind(city,state,zipcode)
# Print a header.
cat("# # # # The First data frame\n")
# Print the data frame.
print(addresses)
# Create another data frame with similar columns
new.address <- data.frame(
city = c("Lowry","Charlotte"),
state = c("CO","FL"),
zipcode = c("80230","33949"),
stringsAsFactors = FALSE
)
# Print a header.
cat("# # # The Second data frame\n")
# Print the data frame.
print(new.address)
# Combine rows form both the data frames.
all.addresses <- rbind(addresses,new.address)
# Print a header.
cat("# # # The combined data frame\n")
# Print the result.
print(all.addresses)Quando executamos o código acima, ele produz o seguinte resultado -
# # # # The First data frame
city state zipcode
[1,] "Tampa" "FL" "33602"
[2,] "Seattle" "WA" "98104"
[3,] "Hartford" "CT" "6161"
[4,] "Denver" "CO" "80294"
# # # The Second data frame
city state zipcode
1 Lowry CO 80230
2 Charlotte FL 33949
# # # The combined data frame
city state zipcode
1 Tampa FL 33602
2 Seattle WA 98104
3 Hartford CT 6161
4 Denver CO 80294
5 Lowry CO 80230
6 Charlotte FL 33949Mesclando Quadros de Dados
Podemos fundir dois quadros de dados usando o merge()função. Os quadros de dados devem ter os mesmos nomes de coluna em que ocorre a fusão.
No exemplo abaixo, consideramos os conjuntos de dados sobre Diabetes em Mulheres Indígenas Pima disponíveis nos nomes de biblioteca "MASSA". mesclamos os dois conjuntos de dados com base nos valores da pressão arterial ("bp") e índice de massa corporal ("bmi"). Ao escolher essas duas colunas para fusão, os registros onde os valores dessas duas variáveis correspondem em ambos os conjuntos de dados são combinados para formar um único quadro de dados.
library(MASS)
merged.Pima <- merge(x = Pima.te, y = Pima.tr,
by.x = c("bp", "bmi"),
by.y = c("bp", "bmi")
)
print(merged.Pima)
nrow(merged.Pima)Quando executamos o código acima, ele produz o seguinte resultado -
bp bmi npreg.x glu.x skin.x ped.x age.x type.x npreg.y glu.y skin.y ped.y
1 60 33.8 1 117 23 0.466 27 No 2 125 20 0.088
2 64 29.7 2 75 24 0.370 33 No 2 100 23 0.368
3 64 31.2 5 189 33 0.583 29 Yes 3 158 13 0.295
4 64 33.2 4 117 27 0.230 24 No 1 96 27 0.289
5 66 38.1 3 115 39 0.150 28 No 1 114 36 0.289
6 68 38.5 2 100 25 0.324 26 No 7 129 49 0.439
7 70 27.4 1 116 28 0.204 21 No 0 124 20 0.254
8 70 33.1 4 91 32 0.446 22 No 9 123 44 0.374
9 70 35.4 9 124 33 0.282 34 No 6 134 23 0.542
10 72 25.6 1 157 21 0.123 24 No 4 99 17 0.294
11 72 37.7 5 95 33 0.370 27 No 6 103 32 0.324
12 74 25.9 9 134 33 0.460 81 No 8 126 38 0.162
13 74 25.9 1 95 21 0.673 36 No 8 126 38 0.162
14 78 27.6 5 88 30 0.258 37 No 6 125 31 0.565
15 78 27.6 10 122 31 0.512 45 No 6 125 31 0.565
16 78 39.4 2 112 50 0.175 24 No 4 112 40 0.236
17 88 34.5 1 117 24 0.403 40 Yes 4 127 11 0.598
age.y type.y
1 31 No
2 21 No
3 24 No
4 21 No
5 21 No
6 43 Yes
7 36 Yes
8 40 No
9 29 Yes
10 28 No
11 55 No
12 39 No
13 39 No
14 49 Yes
15 49 Yes
16 38 No
17 28 No
[1] 17Derretimento e Fundição
Um dos aspectos mais interessantes da programação R é sobre como alterar a forma dos dados em várias etapas para obter a forma desejada. As funções usadas para fazer isso são chamadasmelt() e cast().
Consideramos o conjunto de dados denominado navios presente na biblioteca denominada "MASSA".
library(MASS)
print(ships)Quando executamos o código acima, ele produz o seguinte resultado -
type year period service incidents
1 A 60 60 127 0
2 A 60 75 63 0
3 A 65 60 1095 3
4 A 65 75 1095 4
5 A 70 60 1512 6
.............
.............
8 A 75 75 2244 11
9 B 60 60 44882 39
10 B 60 75 17176 29
11 B 65 60 28609 58
............
............
17 C 60 60 1179 1
18 C 60 75 552 1
19 C 65 60 781 0
............
............Derreta os dados
Agora, fundimos os dados para organizá-los, convertendo todas as colunas, exceto tipo e ano, em várias linhas.
molten.ships <- melt(ships, id = c("type","year"))
print(molten.ships)Quando executamos o código acima, ele produz o seguinte resultado -
type year variable value
1 A 60 period 60
2 A 60 period 75
3 A 65 period 60
4 A 65 period 75
............
............
9 B 60 period 60
10 B 60 period 75
11 B 65 period 60
12 B 65 period 75
13 B 70 period 60
...........
...........
41 A 60 service 127
42 A 60 service 63
43 A 65 service 1095
...........
...........
70 D 70 service 1208
71 D 75 service 0
72 D 75 service 2051
73 E 60 service 45
74 E 60 service 0
75 E 65 service 789
...........
...........
101 C 70 incidents 6
102 C 70 incidents 2
103 C 75 incidents 0
104 C 75 incidents 1
105 D 60 incidents 0
106 D 60 incidents 0
...........
...........Lance os dados fundidos
Podemos lançar os dados fundidos em uma nova forma, onde o agregado de cada tipo de navio para cada ano é criado. Isso é feito usando ocast() função.
recasted.ship <- cast(molten.ships, type+year~variable,sum)
print(recasted.ship)Quando executamos o código acima, ele produz o seguinte resultado -
type year period service incidents
1 A 60 135 190 0
2 A 65 135 2190 7
3 A 70 135 4865 24
4 A 75 135 2244 11
5 B 60 135 62058 68
6 B 65 135 48979 111
7 B 70 135 20163 56
8 B 75 135 7117 18
9 C 60 135 1731 2
10 C 65 135 1457 1
11 C 70 135 2731 8
12 C 75 135 274 1
13 D 60 135 356 0
14 D 65 135 480 0
15 D 70 135 1557 13
16 D 75 135 2051 4
17 E 60 135 45 0
18 E 65 135 1226 14
19 E 70 135 3318 17
20 E 75 135 542 1Em R, podemos ler dados de arquivos armazenados fora do ambiente R. Também podemos gravar dados em arquivos que serão armazenados e acessados pelo sistema operacional. R pode ler e gravar em vários formatos de arquivo como csv, excel, xml etc.
Neste capítulo, aprenderemos a ler dados de um arquivo csv e, a seguir, gravar dados em um arquivo csv. O arquivo deve estar presente no diretório de trabalho atual para que R possa lê-lo. Claro que também podemos definir nosso próprio diretório e ler os arquivos a partir dele.
Obtendo e configurando o diretório de trabalho
Você pode verificar para qual diretório o espaço de trabalho R está apontando usando o getwd()função. Você também pode definir um novo diretório de trabalho usandosetwd()função.
# Get and print current working directory.
print(getwd())
# Set current working directory.
setwd("/web/com")
# Get and print current working directory.
print(getwd())Quando executamos o código acima, ele produz o seguinte resultado -
[1] "/web/com/1441086124_2016"
[1] "/web/com"Este resultado depende do seu sistema operacional e do diretório atual onde você está trabalhando.
Entrada como arquivo CSV
O arquivo csv é um arquivo de texto no qual os valores nas colunas são separados por uma vírgula. Vamos considerar os seguintes dados presentes no arquivo chamadoinput.csv.
Você pode criar esse arquivo usando o bloco de notas do Windows, copiando e colando esses dados. Salve o arquivo comoinput.csv usando a opção salvar como todos os arquivos (*. *) no bloco de notas.
id,name,salary,start_date,dept
1,Rick,623.3,2012-01-01,IT
2,Dan,515.2,2013-09-23,Operations
3,Michelle,611,2014-11-15,IT
4,Ryan,729,2014-05-11,HR
5,Gary,843.25,2015-03-27,Finance
6,Nina,578,2013-05-21,IT
7,Simon,632.8,2013-07-30,Operations
8,Guru,722.5,2014-06-17,FinanceLer um arquivo CSV
A seguir está um exemplo simples de read.csv() função para ler um arquivo CSV disponível em seu diretório de trabalho atual -
data <- read.csv("input.csv")
print(data)Quando executamos o código acima, ele produz o seguinte resultado -
id, name, salary, start_date, dept
1 1 Rick 623.30 2012-01-01 IT
2 2 Dan 515.20 2013-09-23 Operations
3 3 Michelle 611.00 2014-11-15 IT
4 4 Ryan 729.00 2014-05-11 HR
5 NA Gary 843.25 2015-03-27 Finance
6 6 Nina 578.00 2013-05-21 IT
7 7 Simon 632.80 2013-07-30 Operations
8 8 Guru 722.50 2014-06-17 FinanceAnalisando o arquivo CSV
Por padrão, o read.csv()função fornece a saída como um quadro de dados. Isso pode ser facilmente verificado da seguinte maneira. Também podemos verificar o número de colunas e linhas.
data <- read.csv("input.csv")
print(is.data.frame(data))
print(ncol(data))
print(nrow(data))Quando executamos o código acima, ele produz o seguinte resultado -
[1] TRUE
[1] 5
[1] 8Depois de ler os dados em um quadro de dados, podemos aplicar todas as funções aplicáveis aos quadros de dados, conforme explicado na seção subsequente.
Obtenha o salário máximo
# Create a data frame.
data <- read.csv("input.csv")
# Get the max salary from data frame.
sal <- max(data$salary)
print(sal)Quando executamos o código acima, ele produz o seguinte resultado -
[1] 843.25Obtenha os detalhes da pessoa com salário máximo
Podemos buscar linhas que atendam a critérios de filtro específicos semelhantes a uma cláusula where do SQL.
# Create a data frame.
data <- read.csv("input.csv")
# Get the max salary from data frame.
sal <- max(data$salary)
# Get the person detail having max salary.
retval <- subset(data, salary == max(salary))
print(retval)Quando executamos o código acima, ele produz o seguinte resultado -
id name salary start_date dept
5 NA Gary 843.25 2015-03-27 FinanceFaça com que todas as pessoas trabalhem no departamento de TI
# Create a data frame.
data <- read.csv("input.csv")
retval <- subset( data, dept == "IT")
print(retval)Quando executamos o código acima, ele produz o seguinte resultado -
id name salary start_date dept
1 1 Rick 623.3 2012-01-01 IT
3 3 Michelle 611.0 2014-11-15 IT
6 6 Nina 578.0 2013-05-21 ITObtenha as pessoas no departamento de TI cujo salário é superior a 600
# Create a data frame.
data <- read.csv("input.csv")
info <- subset(data, salary > 600 & dept == "IT")
print(info)Quando executamos o código acima, ele produz o seguinte resultado -
id name salary start_date dept
1 1 Rick 623.3 2012-01-01 IT
3 3 Michelle 611.0 2014-11-15 ITObtenha as pessoas que aderiram em ou depois de 2014
# Create a data frame.
data <- read.csv("input.csv")
retval <- subset(data, as.Date(start_date) > as.Date("2014-01-01"))
print(retval)Quando executamos o código acima, ele produz o seguinte resultado -
id name salary start_date dept
3 3 Michelle 611.00 2014-11-15 IT
4 4 Ryan 729.00 2014-05-11 HR
5 NA Gary 843.25 2015-03-27 Finance
8 8 Guru 722.50 2014-06-17 FinanceGravando em um arquivo CSV
R pode criar um arquivo csv a partir de um quadro de dados existente. owrite.csv()função é usada para criar o arquivo csv. Este arquivo é criado no diretório de trabalho.
# Create a data frame.
data <- read.csv("input.csv")
retval <- subset(data, as.Date(start_date) > as.Date("2014-01-01"))
# Write filtered data into a new file.
write.csv(retval,"output.csv")
newdata <- read.csv("output.csv")
print(newdata)Quando executamos o código acima, ele produz o seguinte resultado -
X id name salary start_date dept
1 3 3 Michelle 611.00 2014-11-15 IT
2 4 4 Ryan 729.00 2014-05-11 HR
3 5 NA Gary 843.25 2015-03-27 Finance
4 8 8 Guru 722.50 2014-06-17 FinanceAqui, a coluna X vem do conjunto de dados newper. Isso pode ser eliminado usando parâmetros adicionais durante a gravação do arquivo.
# Create a data frame.
data <- read.csv("input.csv")
retval <- subset(data, as.Date(start_date) > as.Date("2014-01-01"))
# Write filtered data into a new file.
write.csv(retval,"output.csv", row.names = FALSE)
newdata <- read.csv("output.csv")
print(newdata)Quando executamos o código acima, ele produz o seguinte resultado -
id name salary start_date dept
1 3 Michelle 611.00 2014-11-15 IT
2 4 Ryan 729.00 2014-05-11 HR
3 NA Gary 843.25 2015-03-27 Finance
4 8 Guru 722.50 2014-06-17 FinanceO Microsoft Excel é o programa de planilhas mais amplamente usado que armazena dados no formato .xls ou .xlsx. R pode ler diretamente desses arquivos usando alguns pacotes específicos do Excel. Poucos pacotes são - XLConnect, xlsx, gdata etc. Estaremos usando o pacote xlsx. R também pode escrever em arquivo excel usando este pacote.
Instale o pacote xlsx
Você pode usar o seguinte comando no console R para instalar o pacote "xlsx". Pode ser necessário instalar alguns pacotes adicionais dos quais este pacote depende. Siga o mesmo comando com o nome do pacote necessário para instalar os pacotes adicionais.
install.packages("xlsx")Verifique e carregue o pacote "xlsx"
Use o seguinte comando para verificar e carregar o pacote "xlsx".
# Verify the package is installed.
any(grepl("xlsx",installed.packages()))
# Load the library into R workspace.
library("xlsx")Quando o script é executado, obtemos a seguinte saída.
[1] TRUE
Loading required package: rJava
Loading required package: methods
Loading required package: xlsxjarsEntrada como arquivo xlsx
Abra o Microsoft Excel. Copie e cole os seguintes dados na planilha chamada planilha1.
id name salary start_date dept
1 Rick 623.3 1/1/2012 IT
2 Dan 515.2 9/23/2013 Operations
3 Michelle 611 11/15/2014 IT
4 Ryan 729 5/11/2014 HR
5 Gary 43.25 3/27/2015 Finance
6 Nina 578 5/21/2013 IT
7 Simon 632.8 7/30/2013 Operations
8 Guru 722.5 6/17/2014 FinanceAlém disso, copie e cole os seguintes dados em outra planilha e renomeie esta planilha para "cidade".
name city
Rick Seattle
Dan Tampa
Michelle Chicago
Ryan Seattle
Gary Houston
Nina Boston
Simon Mumbai
Guru DallasSalve o arquivo Excel como "input.xlsx". Você deve salvá-lo no diretório de trabalho atual da área de trabalho R.
Lendo o arquivo Excel
O input.xlsx é lido usando o read.xlsx()função conforme mostrado abaixo. O resultado é armazenado como um quadro de dados no ambiente R.
# Read the first worksheet in the file input.xlsx.
data <- read.xlsx("input.xlsx", sheetIndex = 1)
print(data)Quando executamos o código acima, ele produz o seguinte resultado -
id, name, salary, start_date, dept
1 1 Rick 623.30 2012-01-01 IT
2 2 Dan 515.20 2013-09-23 Operations
3 3 Michelle 611.00 2014-11-15 IT
4 4 Ryan 729.00 2014-05-11 HR
5 NA Gary 843.25 2015-03-27 Finance
6 6 Nina 578.00 2013-05-21 IT
7 7 Simon 632.80 2013-07-30 Operations
8 8 Guru 722.50 2014-06-17 FinanceUm arquivo binário é um arquivo que contém informações armazenadas apenas na forma de bits e bytes (0's e 1's). Eles não são legíveis por humanos, pois os bytes neles se traduzem em caracteres e símbolos que contêm muitos outros caracteres não imprimíveis. A tentativa de ler um arquivo binário usando qualquer editor de texto mostrará caracteres como Ø e ð.
O arquivo binário deve ser lido por programas específicos para ser utilizável. Por exemplo, o arquivo binário de um programa Microsoft Word pode ser lido em um formato legível apenas pelo programa Word. O que indica que, além do texto legível por humanos, há muito mais informações como formatação de caracteres e números de página, etc., que também são armazenados junto com caracteres alfanuméricos. E, finalmente, um arquivo binário é uma sequência contínua de bytes. A quebra de linha que vemos em um arquivo de texto é um caractere que une a primeira linha à próxima.
Às vezes, os dados gerados por outros programas precisam ser processados por R como um arquivo binário. Além disso, R é necessário para criar arquivos binários que podem ser compartilhados com outros programas.
R tem duas funções WriteBin() e readBin() para criar e ler arquivos binários.
Sintaxe
writeBin(object, con)
readBin(con, what, n )A seguir está a descrição dos parâmetros usados -
con é o objeto de conexão para ler ou gravar o arquivo binário.
object é o arquivo binário a ser gravado.
what é o modo como caractere, inteiro etc. que representa os bytes a serem lidos.
n é o número de bytes a serem lidos do arquivo binário.
Exemplo
Consideramos os dados embutidos de R como "mtcars". Primeiro, criamos um arquivo csv a partir dele e o convertemos em um arquivo binário e o armazenamos como um arquivo do sistema operacional. Em seguida, lemos este arquivo binário criado em R.
Escrevendo o arquivo binário
Lemos o quadro de dados "mtcars" como um arquivo csv e depois o gravamos como um arquivo binário no sistema operacional.
# Read the "mtcars" data frame as a csv file and store only the columns
"cyl", "am" and "gear".
write.table(mtcars, file = "mtcars.csv",row.names = FALSE, na = "",
col.names = TRUE, sep = ",")
# Store 5 records from the csv file as a new data frame.
new.mtcars <- read.table("mtcars.csv",sep = ",",header = TRUE,nrows = 5)
# Create a connection object to write the binary file using mode "wb".
write.filename = file("/web/com/binmtcars.dat", "wb")
# Write the column names of the data frame to the connection object.
writeBin(colnames(new.mtcars), write.filename)
# Write the records in each of the column to the file.
writeBin(c(new.mtcars$cyl,new.mtcars$am,new.mtcars$gear), write.filename)
# Close the file for writing so that it can be read by other program.
close(write.filename)Lendo o arquivo binário
O arquivo binário criado acima armazena todos os dados como bytes contínuos. Portanto, vamos lê-lo escolhendo os valores apropriados dos nomes das colunas, bem como os valores das colunas.
# Create a connection object to read the file in binary mode using "rb".
read.filename <- file("/web/com/binmtcars.dat", "rb")
# First read the column names. n = 3 as we have 3 columns.
column.names <- readBin(read.filename, character(), n = 3)
# Next read the column values. n = 18 as we have 3 column names and 15 values.
read.filename <- file("/web/com/binmtcars.dat", "rb")
bindata <- readBin(read.filename, integer(), n = 18)
# Print the data.
print(bindata)
# Read the values from 4th byte to 8th byte which represents "cyl".
cyldata = bindata[4:8]
print(cyldata)
# Read the values form 9th byte to 13th byte which represents "am".
amdata = bindata[9:13]
print(amdata)
# Read the values form 9th byte to 13th byte which represents "gear".
geardata = bindata[14:18]
print(geardata)
# Combine all the read values to a dat frame.
finaldata = cbind(cyldata, amdata, geardata)
colnames(finaldata) = column.names
print(finaldata)Quando executamos o código acima, ele produz o seguinte resultado e gráfico -
[1] 7108963 1728081249 7496037 6 6 4
[7] 6 8 1 1 1 0
[13] 0 4 4 4 3 3
[1] 6 6 4 6 8
[1] 1 1 1 0 0
[1] 4 4 4 3 3
cyl am gear
[1,] 6 1 4
[2,] 6 1 4
[3,] 4 1 4
[4,] 6 0 3
[5,] 8 0 3Como podemos ver, recuperamos os dados originais lendo o arquivo binário em R.
XML é um formato de arquivo que compartilha o formato de arquivo e os dados na World Wide Web, intranets e em outros lugares usando texto ASCII padrão. Significa Extensible Markup Language (XML). Semelhante ao HTML, ele contém tags de marcação. Mas, ao contrário do HTML, onde a tag de marcação descreve a estrutura da página, em xml as tags de marcação descrevem o significado dos dados contidos no arquivo.
Você pode ler um arquivo xml em R usando o pacote "XML". Este pacote pode ser instalado usando o seguinte comando.
install.packages("XML")Dados de entrada
Crie um arquivo XMl copiando os dados abaixo em um editor de texto como o bloco de notas. Salve o arquivo com um.xml extensão e escolher o tipo de arquivo como all files(*.*).
<RECORDS>
<EMPLOYEE>
<ID>1</ID>
<NAME>Rick</NAME>
<SALARY>623.3</SALARY>
<STARTDATE>1/1/2012</STARTDATE>
<DEPT>IT</DEPT>
</EMPLOYEE>
<EMPLOYEE>
<ID>2</ID>
<NAME>Dan</NAME>
<SALARY>515.2</SALARY>
<STARTDATE>9/23/2013</STARTDATE>
<DEPT>Operations</DEPT>
</EMPLOYEE>
<EMPLOYEE>
<ID>3</ID>
<NAME>Michelle</NAME>
<SALARY>611</SALARY>
<STARTDATE>11/15/2014</STARTDATE>
<DEPT>IT</DEPT>
</EMPLOYEE>
<EMPLOYEE>
<ID>4</ID>
<NAME>Ryan</NAME>
<SALARY>729</SALARY>
<STARTDATE>5/11/2014</STARTDATE>
<DEPT>HR</DEPT>
</EMPLOYEE>
<EMPLOYEE>
<ID>5</ID>
<NAME>Gary</NAME>
<SALARY>843.25</SALARY>
<STARTDATE>3/27/2015</STARTDATE>
<DEPT>Finance</DEPT>
</EMPLOYEE>
<EMPLOYEE>
<ID>6</ID>
<NAME>Nina</NAME>
<SALARY>578</SALARY>
<STARTDATE>5/21/2013</STARTDATE>
<DEPT>IT</DEPT>
</EMPLOYEE>
<EMPLOYEE>
<ID>7</ID>
<NAME>Simon</NAME>
<SALARY>632.8</SALARY>
<STARTDATE>7/30/2013</STARTDATE>
<DEPT>Operations</DEPT>
</EMPLOYEE>
<EMPLOYEE>
<ID>8</ID>
<NAME>Guru</NAME>
<SALARY>722.5</SALARY>
<STARTDATE>6/17/2014</STARTDATE>
<DEPT>Finance</DEPT>
</EMPLOYEE>
</RECORDS>Lendo Arquivo XML
O arquivo xml é lido por R usando a função xmlParse(). Ele é armazenado como uma lista em R.
# Load the package required to read XML files.
library("XML")
# Also load the other required package.
library("methods")
# Give the input file name to the function.
result <- xmlParse(file = "input.xml")
# Print the result.
print(result)Quando executamos o código acima, ele produz o seguinte resultado -
1
Rick
623.3
1/1/2012
IT
2
Dan
515.2
9/23/2013
Operations
3
Michelle
611
11/15/2014
IT
4
Ryan
729
5/11/2014
HR
5
Gary
843.25
3/27/2015
Finance
6
Nina
578
5/21/2013
IT
7
Simon
632.8
7/30/2013
Operations
8
Guru
722.5
6/17/2014
FinanceObtenha o número de nós presentes no arquivo XML
# Load the packages required to read XML files.
library("XML")
library("methods")
# Give the input file name to the function.
result <- xmlParse(file = "input.xml")
# Exract the root node form the xml file.
rootnode <- xmlRoot(result)
# Find number of nodes in the root.
rootsize <- xmlSize(rootnode)
# Print the result.
print(rootsize)Quando executamos o código acima, ele produz o seguinte resultado -
output
[1] 8Detalhes do primeiro nó
Vejamos o primeiro registro do arquivo analisado. Isso nos dará uma ideia dos vários elementos presentes no nó de nível superior.
# Load the packages required to read XML files.
library("XML")
library("methods")
# Give the input file name to the function.
result <- xmlParse(file = "input.xml")
# Exract the root node form the xml file.
rootnode <- xmlRoot(result)
# Print the result.
print(rootnode[1])Quando executamos o código acima, ele produz o seguinte resultado -
$EMPLOYEE
1
Rick
623.3
1/1/2012
IT
attr(,"class")
[1] "XMLInternalNodeList" "XMLNodeList"Obtenha diferentes elementos de um nó
# Load the packages required to read XML files.
library("XML")
library("methods")
# Give the input file name to the function.
result <- xmlParse(file = "input.xml")
# Exract the root node form the xml file.
rootnode <- xmlRoot(result)
# Get the first element of the first node.
print(rootnode[[1]][[1]])
# Get the fifth element of the first node.
print(rootnode[[1]][[5]])
# Get the second element of the third node.
print(rootnode[[3]][[2]])Quando executamos o código acima, ele produz o seguinte resultado -
1
IT
MichelleXML para quadro de dados
Para lidar com os dados de forma eficaz em arquivos grandes, lemos os dados no arquivo xml como um quadro de dados. Em seguida, processe o quadro de dados para análise de dados.
# Load the packages required to read XML files.
library("XML")
library("methods")
# Convert the input xml file to a data frame.
xmldataframe <- xmlToDataFrame("input.xml")
print(xmldataframe)Quando executamos o código acima, ele produz o seguinte resultado -
ID NAME SALARY STARTDATE DEPT
1 1 Rick 623.30 2012-01-01 IT
2 2 Dan 515.20 2013-09-23 Operations
3 3 Michelle 611.00 2014-11-15 IT
4 4 Ryan 729.00 2014-05-11 HR
5 NA Gary 843.25 2015-03-27 Finance
6 6 Nina 578.00 2013-05-21 IT
7 7 Simon 632.80 2013-07-30 Operations
8 8 Guru 722.50 2014-06-17 FinanceComo os dados agora estão disponíveis como um quadro de dados, podemos usar a função relacionada ao quadro de dados para ler e manipular o arquivo.
O arquivo JSON armazena dados como texto em formato legível por humanos. Json significa JavaScript Object Notation. R pode ler arquivos JSON usando o pacote rjson.
Instale o pacote rjson
No console R, você pode emitir o seguinte comando para instalar o pacote rjson.
install.packages("rjson")Dados de entrada
Crie um arquivo JSON copiando os dados abaixo em um editor de texto como o bloco de notas. Salve o arquivo com um.json extensão e escolher o tipo de arquivo como all files(*.*).
{
"ID":["1","2","3","4","5","6","7","8" ],
"Name":["Rick","Dan","Michelle","Ryan","Gary","Nina","Simon","Guru" ],
"Salary":["623.3","515.2","611","729","843.25","578","632.8","722.5" ],
"StartDate":[ "1/1/2012","9/23/2013","11/15/2014","5/11/2014","3/27/2015","5/21/2013",
"7/30/2013","6/17/2014"],
"Dept":[ "IT","Operations","IT","HR","Finance","IT","Operations","Finance"]
}Leia o arquivo JSON
O arquivo JSON é lido por R usando a função de JSON(). Ele é armazenado como uma lista em R.
# Load the package required to read JSON files.
library("rjson")
# Give the input file name to the function.
result <- fromJSON(file = "input.json")
# Print the result.
print(result)Quando executamos o código acima, ele produz o seguinte resultado -
$ID
[1] "1" "2" "3" "4" "5" "6" "7" "8"
$Name [1] "Rick" "Dan" "Michelle" "Ryan" "Gary" "Nina" "Simon" "Guru" $Salary
[1] "623.3" "515.2" "611" "729" "843.25" "578" "632.8" "722.5"
$StartDate [1] "1/1/2012" "9/23/2013" "11/15/2014" "5/11/2014" "3/27/2015" "5/21/2013" "7/30/2013" "6/17/2014" $Dept
[1] "IT" "Operations" "IT" "HR" "Finance" "IT"
"Operations" "Finance"Converter JSON em um quadro de dados
Podemos converter os dados extraídos acima para um quadro de dados R para análise posterior usando o as.data.frame() função.
# Load the package required to read JSON files.
library("rjson")
# Give the input file name to the function.
result <- fromJSON(file = "input.json")
# Convert JSON file to a data frame.
json_data_frame <- as.data.frame(result)
print(json_data_frame)Quando executamos o código acima, ele produz o seguinte resultado -
id, name, salary, start_date, dept
1 1 Rick 623.30 2012-01-01 IT
2 2 Dan 515.20 2013-09-23 Operations
3 3 Michelle 611.00 2014-11-15 IT
4 4 Ryan 729.00 2014-05-11 HR
5 NA Gary 843.25 2015-03-27 Finance
6 6 Nina 578.00 2013-05-21 IT
7 7 Simon 632.80 2013-07-30 Operations
8 8 Guru 722.50 2014-06-17 FinanceMuitos sites fornecem dados para consumo por seus usuários. Por exemplo, a Organização Mundial da Saúde (OMS) fornece relatórios sobre informações médicas e de saúde na forma de arquivos CSV, txt e XML. Usando programas R, podemos extrair programaticamente dados específicos de tais sites. Alguns pacotes em R que são usados para sucatear dados da web são - "RCurl", XML "e" stringr ". Eles são usados para se conectar aos URLs, identificar os links necessários para os arquivos e baixá-los para o ambiente local.
Instale pacotes R
Os pacotes a seguir são necessários para o processamento de URLs e links para os arquivos. Se eles não estiverem disponíveis em seu ambiente R, você pode instalá-los usando os seguintes comandos.
install.packages("RCurl")
install.packages("XML")
install.packages("stringr")
install.packages("plyr")Dados de entrada
Iremos visitar os dados meteorológicos do URL e baixar os arquivos CSV usando R para o ano de 2015.
Exemplo
Vamos usar a função getHTMLLinks()para reunir os URLs dos arquivos. Então usaremos a funçãodownload.file()para salvar os arquivos no sistema local. Como aplicaremos o mesmo código repetidamente para vários arquivos, criaremos uma função a ser chamada várias vezes. Os nomes dos arquivos são passados como parâmetros na forma de um objeto de lista R para esta função.
# Read the URL.
url <- "http://www.geos.ed.ac.uk/~weather/jcmb_ws/"
# Gather the html links present in the webpage.
links <- getHTMLLinks(url)
# Identify only the links which point to the JCMB 2015 files.
filenames <- links[str_detect(links, "JCMB_2015")]
# Store the file names as a list.
filenames_list <- as.list(filenames)
# Create a function to download the files by passing the URL and filename list.
downloadcsv <- function (mainurl,filename) {
filedetails <- str_c(mainurl,filename)
download.file(filedetails,filename)
}
# Now apply the l_ply function and save the files into the current R working directory.
l_ply(filenames,downloadcsv,mainurl = "http://www.geos.ed.ac.uk/~weather/jcmb_ws/")Verifique o download do arquivo
Após executar o código acima, você pode localizar os seguintes arquivos no diretório de trabalho R atual.
"JCMB_2015.csv" "JCMB_2015_Apr.csv" "JCMB_2015_Feb.csv" "JCMB_2015_Jan.csv"
"JCMB_2015_Mar.csv"Os dados são sistemas de banco de dados relacional são armazenados em um formato normalizado. Portanto, para realizar computação estatística, precisaremos de consultas SQL muito avançadas e complexas. Mas R pode se conectar facilmente a muitos bancos de dados relacionais como MySql, Oracle, servidor Sql etc. e buscar registros deles como um quadro de dados. Uma vez que os dados estão disponíveis no ambiente R, eles se tornam um conjunto de dados R normal e podem ser manipulados ou analisados usando todos os pacotes e funções poderosos.
Neste tutorial, usaremos MySql como nosso banco de dados de referência para conexão com R.
Pacote RMySQL
R tem um pacote integrado denominado "RMySQL" que fornece conectividade nativa entre com o banco de dados MySql. Você pode instalar este pacote no ambiente R usando o seguinte comando.
install.packages("RMySQL")Conectando R ao MySql
Uma vez que o pacote é instalado, criamos um objeto de conexão em R para conectar ao banco de dados. Leva o nome de usuário, senha, nome do banco de dados e nome do host como entrada.
# Create a connection Object to MySQL database.
# We will connect to the sampel database named "sakila" that comes with MySql installation.
mysqlconnection = dbConnect(MySQL(), user = 'root', password = '', dbname = 'sakila',
host = 'localhost')
# List the tables available in this database.
dbListTables(mysqlconnection)Quando executamos o código acima, ele produz o seguinte resultado -
[1] "actor" "actor_info"
[3] "address" "category"
[5] "city" "country"
[7] "customer" "customer_list"
[9] "film" "film_actor"
[11] "film_category" "film_list"
[13] "film_text" "inventory"
[15] "language" "nicer_but_slower_film_list"
[17] "payment" "rental"
[19] "sales_by_film_category" "sales_by_store"
[21] "staff" "staff_list"
[23] "store"Consultando as tabelas
Podemos consultar as tabelas do banco de dados no MySql usando a função dbSendQuery(). A consulta é executada no MySql e o conjunto de resultados é retornado usando o Rfetch()função. Finalmente, ele é armazenado como um quadro de dados em R.
# Query the "actor" tables to get all the rows.
result = dbSendQuery(mysqlconnection, "select * from actor")
# Store the result in a R data frame object. n = 5 is used to fetch first 5 rows.
data.frame = fetch(result, n = 5)
print(data.fame)Quando executamos o código acima, ele produz o seguinte resultado -
actor_id first_name last_name last_update
1 1 PENELOPE GUINESS 2006-02-15 04:34:33
2 2 NICK WAHLBERG 2006-02-15 04:34:33
3 3 ED CHASE 2006-02-15 04:34:33
4 4 JENNIFER DAVIS 2006-02-15 04:34:33
5 5 JOHNNY LOLLOBRIGIDA 2006-02-15 04:34:33Consulta com cláusula de filtro
Podemos passar qualquer consulta de seleção válida para obter o resultado.
result = dbSendQuery(mysqlconnection, "select * from actor where last_name = 'TORN'")
# Fetch all the records(with n = -1) and store it as a data frame.
data.frame = fetch(result, n = -1)
print(data)Quando executamos o código acima, ele produz o seguinte resultado -
actor_id first_name last_name last_update
1 18 DAN TORN 2006-02-15 04:34:33
2 94 KENNETH TORN 2006-02-15 04:34:33
3 102 WALTER TORN 2006-02-15 04:34:33Atualizando linhas nas tabelas
Podemos atualizar as linhas em uma tabela Mysql passando a consulta de atualização para a função dbSendQuery ().
dbSendQuery(mysqlconnection, "update mtcars set disp = 168.5 where hp = 110")Após executar o código acima podemos ver a tabela atualizada no ambiente MySql.
Inserindo Dados nas Tabelas
dbSendQuery(mysqlconnection,
"insert into mtcars(row_names, mpg, cyl, disp, hp, drat, wt, qsec, vs, am, gear, carb)
values('New Mazda RX4 Wag', 21, 6, 168.5, 110, 3.9, 2.875, 17.02, 0, 1, 4, 4)"
)Após executar o código acima, podemos ver a linha inserida na tabela no ambiente MySql.
Criação de tabelas no MySql
Podemos criar tabelas no MySql usando a função dbWriteTable(). Ele sobrescreve a tabela se ela já existir e leva um quadro de dados como entrada.
# Create the connection object to the database where we want to create the table.
mysqlconnection = dbConnect(MySQL(), user = 'root', password = '', dbname = 'sakila',
host = 'localhost')
# Use the R data frame "mtcars" to create the table in MySql.
# All the rows of mtcars are taken inot MySql.
dbWriteTable(mysqlconnection, "mtcars", mtcars[, ], overwrite = TRUE)Após executar o código acima, podemos ver a tabela criada no ambiente MySql.
Eliminando tabelas no MySql
Podemos eliminar as tabelas no banco de dados MySql passando a instrução drop table em dbSendQuery () da mesma forma que usamos para consultar dados de tabelas.
dbSendQuery(mysqlconnection, 'drop table if exists mtcars')Depois de executar o código acima, podemos ver que a tabela foi descartada no ambiente MySql.
A linguagem de programação R possui inúmeras bibliotecas para criar tabelas e gráficos. Um gráfico de pizza é uma representação de valores como fatias de um círculo com cores diferentes. As fatias são rotuladas e os números correspondentes a cada fatia também são representados no gráfico.
Em R, o gráfico de pizza é criado usando o pie()função que recebe números positivos como uma entrada vetorial. Os parâmetros adicionais são usados para controlar rótulos, cor, título, etc.
Sintaxe
A sintaxe básica para criar um gráfico de pizza usando o R é -
pie(x, labels, radius, main, col, clockwise)A seguir está a descrição dos parâmetros usados -
x é um vetor que contém os valores numéricos usados no gráfico de pizza.
labels é usado para descrever as fatias.
radius indica o raio do círculo do gráfico de pizza. (valor entre -1 e +1).
main indica o título do gráfico.
col indica a paleta de cores.
clockwise é um valor lógico que indica se as fatias são desenhadas no sentido horário ou anti-horário.
Exemplo
Um gráfico de pizza muito simples é criado usando apenas o vetor de entrada e os rótulos. O script a seguir criará e salvará o gráfico de pizza no diretório de trabalho R atual.
# Create data for the graph.
x <- c(21, 62, 10, 53)
labels <- c("London", "New York", "Singapore", "Mumbai")
# Give the chart file a name.
png(file = "city.png")
# Plot the chart.
pie(x,labels)
# Save the file.
dev.off()Quando executamos o código acima, ele produz o seguinte resultado -
Título e cores do gráfico de pizza
Podemos expandir os recursos do gráfico adicionando mais parâmetros à função. Usaremos parâmetromain adicionar um título ao gráfico e outro parâmetro é colque fará uso da paleta de cores do arco-íris ao desenhar o gráfico. O comprimento do palete deve ser igual ao número de valores que temos para o gráfico. Portanto, usamos comprimento (x).
Exemplo
O script a seguir criará e salvará o gráfico de pizza no diretório de trabalho R atual.
# Create data for the graph.
x <- c(21, 62, 10, 53)
labels <- c("London", "New York", "Singapore", "Mumbai")
# Give the chart file a name.
png(file = "city_title_colours.jpg")
# Plot the chart with title and rainbow color pallet.
pie(x, labels, main = "City pie chart", col = rainbow(length(x)))
# Save the file.
dev.off()Quando executamos o código acima, ele produz o seguinte resultado -
Porcentagens da fatia e legenda do gráfico
Podemos adicionar a porcentagem da fatia e uma legenda do gráfico criando variáveis de gráfico adicionais.
# Create data for the graph.
x <- c(21, 62, 10,53)
labels <- c("London","New York","Singapore","Mumbai")
piepercent<- round(100*x/sum(x), 1)
# Give the chart file a name.
png(file = "city_percentage_legends.jpg")
# Plot the chart.
pie(x, labels = piepercent, main = "City pie chart",col = rainbow(length(x)))
legend("topright", c("London","New York","Singapore","Mumbai"), cex = 0.8,
fill = rainbow(length(x)))
# Save the file.
dev.off()Quando executamos o código acima, ele produz o seguinte resultado -
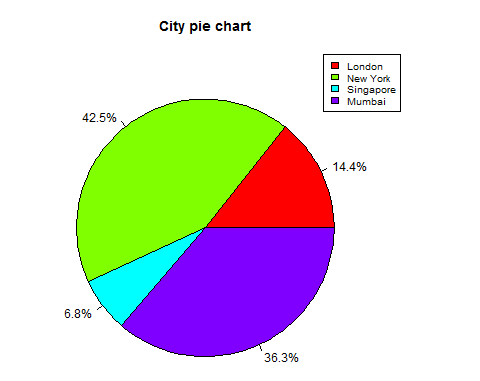
Gráfico Circular 3D
Um gráfico de pizza com 3 dimensões pode ser desenhado usando pacotes adicionais. O pacoteplotrix tem uma função chamada pie3D() que é usado para isso.
# Get the library.
library(plotrix)
# Create data for the graph.
x <- c(21, 62, 10,53)
lbl <- c("London","New York","Singapore","Mumbai")
# Give the chart file a name.
png(file = "3d_pie_chart.jpg")
# Plot the chart.
pie3D(x,labels = lbl,explode = 0.1, main = "Pie Chart of Countries ")
# Save the file.
dev.off()Quando executamos o código acima, ele produz o seguinte resultado -
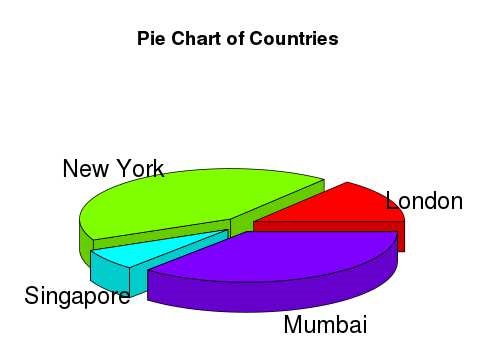
Um gráfico de barras representa os dados em barras retangulares com comprimento da barra proporcional ao valor da variável. R usa a funçãobarplot()para criar gráficos de barras. R pode desenhar barras verticais e horizontais no gráfico de barras. No gráfico de barras, cada uma das barras pode receber cores diferentes.
Sintaxe
A sintaxe básica para criar um gráfico de barras em R é -
barplot(H,xlab,ylab,main, names.arg,col)A seguir está a descrição dos parâmetros usados -
- H é um vetor ou matriz que contém valores numéricos usados no gráfico de barras.
- xlab é o rótulo do eixo x.
- ylab é o rótulo do eixo y.
- main é o título do gráfico de barras.
- names.arg é um vetor de nomes que aparecem em cada barra.
- col é usado para dar cores às barras do gráfico.
Exemplo
Um gráfico de barras simples é criado usando apenas o vetor de entrada e o nome de cada barra.
O script a seguir criará e salvará o gráfico de barras no diretório de trabalho R atual.
# Create the data for the chart
H <- c(7,12,28,3,41)
# Give the chart file a name
png(file = "barchart.png")
# Plot the bar chart
barplot(H)
# Save the file
dev.off()Quando executamos o código acima, ele produz o seguinte resultado -
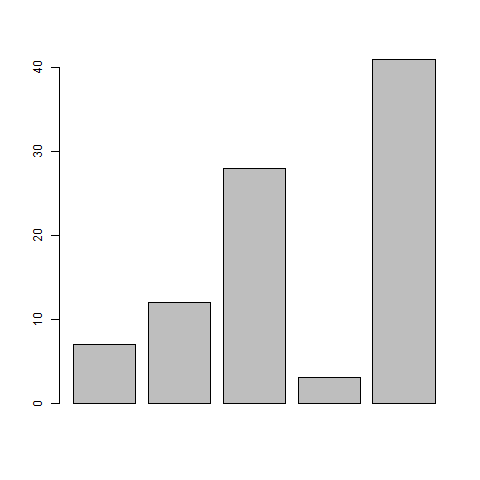
Etiquetas, título e cores do gráfico de barras
Os recursos do gráfico de barras podem ser expandidos adicionando mais parâmetros. omain parâmetro é usado para adicionar title. ocolparâmetro é usado para adicionar cores às barras. oargs.name é um vetor com o mesmo número de valores que o vetor de entrada para descrever o significado de cada barra.
Exemplo
O script a seguir criará e salvará o gráfico de barras no diretório de trabalho R atual.
# Create the data for the chart
H <- c(7,12,28,3,41)
M <- c("Mar","Apr","May","Jun","Jul")
# Give the chart file a name
png(file = "barchart_months_revenue.png")
# Plot the bar chart
barplot(H,names.arg=M,xlab="Month",ylab="Revenue",col="blue",
main="Revenue chart",border="red")
# Save the file
dev.off()Quando executamos o código acima, ele produz o seguinte resultado -
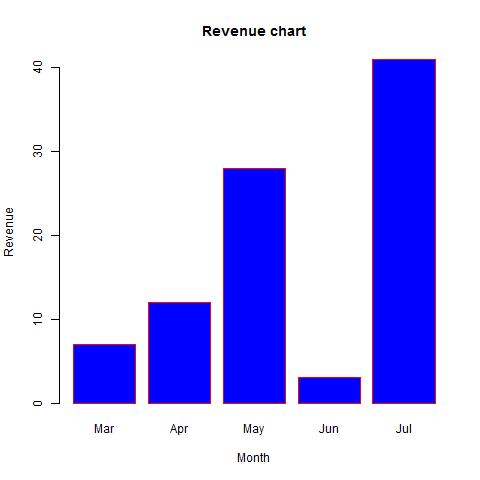
Gráfico de barras de grupo e gráfico de barras empilhadas
Podemos criar gráfico de barras com grupos de barras e pilhas em cada barra usando uma matriz como valores de entrada.
Mais de duas variáveis são representadas como uma matriz que é usada para criar o gráfico de barras do grupo e o gráfico de barras empilhadas.
# Create the input vectors.
colors = c("green","orange","brown")
months <- c("Mar","Apr","May","Jun","Jul")
regions <- c("East","West","North")
# Create the matrix of the values.
Values <- matrix(c(2,9,3,11,9,4,8,7,3,12,5,2,8,10,11), nrow = 3, ncol = 5, byrow = TRUE)
# Give the chart file a name
png(file = "barchart_stacked.png")
# Create the bar chart
barplot(Values, main = "total revenue", names.arg = months, xlab = "month", ylab = "revenue", col = colors)
# Add the legend to the chart
legend("topleft", regions, cex = 1.3, fill = colors)
# Save the file
dev.off()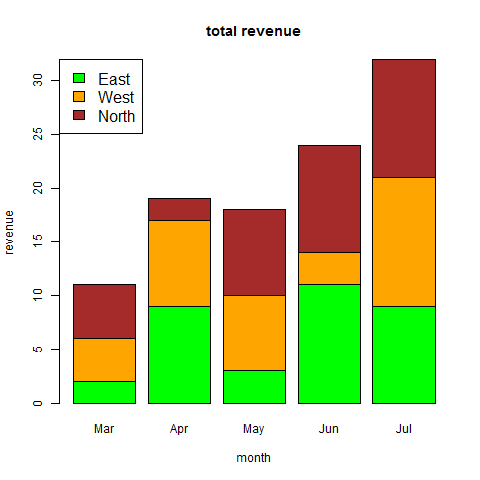
Os boxplots são uma medida de quão bem distribuídos estão os dados em um conjunto de dados. Ele divide o conjunto de dados em três quartis. Este gráfico representa o mínimo, máximo, mediana, primeiro quartil e terceiro quartil no conjunto de dados. Também é útil para comparar a distribuição de dados entre conjuntos de dados desenhando boxplots para cada um deles.
Boxplots são criados em R usando o boxplot() função.
Sintaxe
A sintaxe básica para criar um boxplot em R é -
boxplot(x, data, notch, varwidth, names, main)A seguir está a descrição dos parâmetros usados -
x é um vetor ou uma fórmula.
data é o quadro de dados.
notché um valor lógico. Defina como TRUE para desenhar um entalhe.
varwidthé um valor lógico. Defina como verdadeiro para desenhar a largura da caixa proporcional ao tamanho da amostra.
names são as etiquetas de grupo que serão impressas em cada boxplot.
main é usado para dar um título ao gráfico.
Exemplo
Usamos o conjunto de dados "mtcars" disponível no ambiente R para criar um boxplot básico. Vejamos as colunas "mpg" e "cyl" nos mtcars.
input <- mtcars[,c('mpg','cyl')]
print(head(input))Quando executamos o código acima, ele produz o seguinte resultado -
mpg cyl
Mazda RX4 21.0 6
Mazda RX4 Wag 21.0 6
Datsun 710 22.8 4
Hornet 4 Drive 21.4 6
Hornet Sportabout 18.7 8
Valiant 18.1 6Criação do Boxplot
O script a seguir criará um gráfico de boxplot para a relação entre mpg (milhas por galão) e cyl (número de cilindros).
# Give the chart file a name.
png(file = "boxplot.png")
# Plot the chart.
boxplot(mpg ~ cyl, data = mtcars, xlab = "Number of Cylinders",
ylab = "Miles Per Gallon", main = "Mileage Data")
# Save the file.
dev.off()Quando executamos o código acima, ele produz o seguinte resultado -
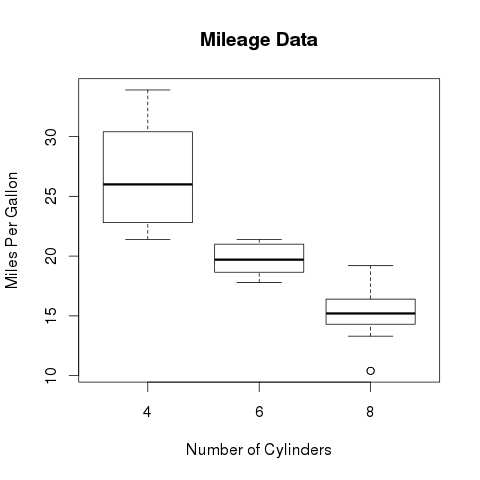
Boxplot com Notch
Podemos desenhar boxplot com entalhe para descobrir como as medianas de diferentes grupos de dados correspondem umas às outras.
O script a seguir criará um gráfico de boxplot com entalhe para cada grupo de dados.
# Give the chart file a name.
png(file = "boxplot_with_notch.png")
# Plot the chart.
boxplot(mpg ~ cyl, data = mtcars,
xlab = "Number of Cylinders",
ylab = "Miles Per Gallon",
main = "Mileage Data",
notch = TRUE,
varwidth = TRUE,
col = c("green","yellow","purple"),
names = c("High","Medium","Low")
)
# Save the file.
dev.off()Quando executamos o código acima, ele produz o seguinte resultado -
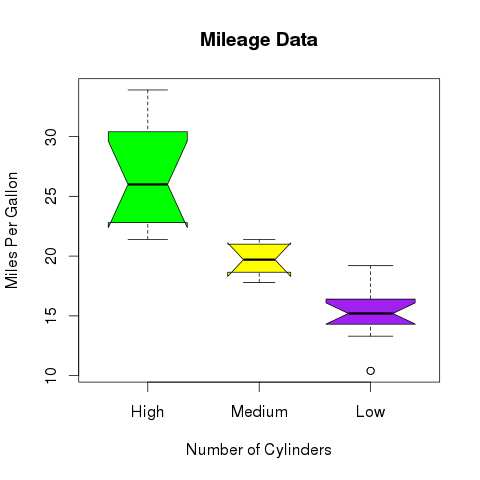
Um histograma representa as frequências dos valores de uma variável dividida em intervalos. O histograma é semelhante ao chat de barra, mas a diferença é que agrupa os valores em intervalos contínuos. Cada barra do histograma representa a altura do número de valores presentes naquele intervalo.
R cria histograma usando hist()função. Esta função recebe um vetor como entrada e usa mais alguns parâmetros para traçar histogramas.
Sintaxe
A sintaxe básica para criar um histograma usando R é -
hist(v,main,xlab,xlim,ylim,breaks,col,border)A seguir está a descrição dos parâmetros usados -
v é um vetor que contém valores numéricos usados no histograma.
main indica o título do gráfico.
col é usado para definir a cor das barras.
border é usado para definir a cor da borda de cada barra.
xlab é usado para dar a descrição do eixo x.
xlim é usado para especificar o intervalo de valores no eixo x.
ylim é usado para especificar o intervalo de valores no eixo y.
breaks é usado para mencionar a largura de cada barra.
Exemplo
Um histograma simples é criado usando parâmetros de vetor, rótulo, col e borda de entrada.
O script fornecido a seguir criará e salvará o histograma no diretório de trabalho R atual.
# Create data for the graph.
v <- c(9,13,21,8,36,22,12,41,31,33,19)
# Give the chart file a name.
png(file = "histogram.png")
# Create the histogram.
hist(v,xlab = "Weight",col = "yellow",border = "blue")
# Save the file.
dev.off()Quando executamos o código acima, ele produz o seguinte resultado -
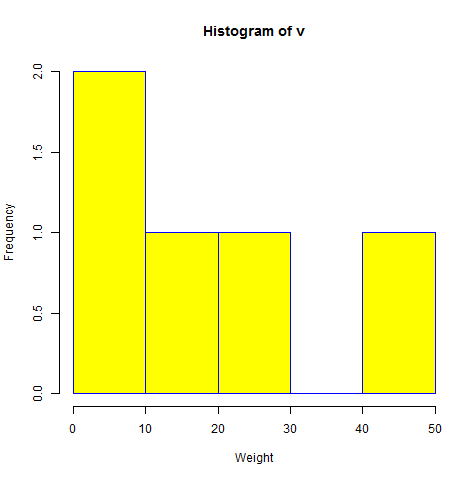
Faixa de valores X e Y
Para especificar a faixa de valores permitidos nos eixos X e Y, podemos usar os parâmetros xlim e ylim.
A largura de cada barra pode ser decidida usando quebras.
# Create data for the graph.
v <- c(9,13,21,8,36,22,12,41,31,33,19)
# Give the chart file a name.
png(file = "histogram_lim_breaks.png")
# Create the histogram.
hist(v,xlab = "Weight",col = "green",border = "red", xlim = c(0,40), ylim = c(0,5),
breaks = 5)
# Save the file.
dev.off()Quando executamos o código acima, ele produz o seguinte resultado -
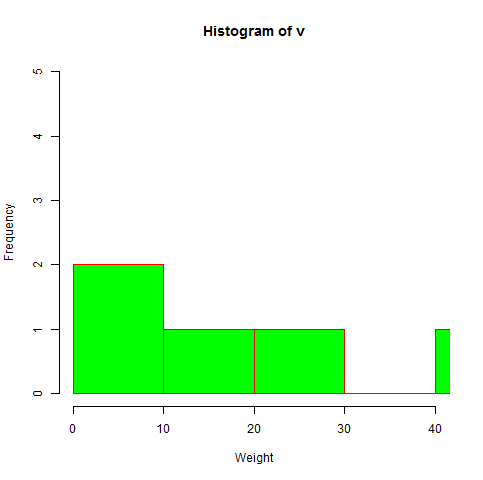
Um gráfico de linha é um gráfico que conecta uma série de pontos desenhando segmentos de linha entre eles. Esses pontos são ordenados em um de seus valores de coordenada (geralmente a coordenada x). Os gráficos de linha são geralmente usados para identificar as tendências nos dados.
o plot() função em R é usada para criar o gráfico de linha.
Sintaxe
A sintaxe básica para criar um gráfico de linha em R é -
plot(v,type,col,xlab,ylab)A seguir está a descrição dos parâmetros usados -
v é um vetor que contém os valores numéricos.
type usa o valor "p" para desenhar apenas os pontos, "l" para desenhar apenas as linhas e "o" para desenhar tanto os pontos quanto as linhas.
xlab é o rótulo do eixo x.
ylab é o rótulo do eixo y.
main é o título do gráfico.
col é usado para dar cores aos pontos e às linhas.
Exemplo
Um gráfico de linha simples é criado usando o vetor de entrada e o parâmetro de tipo como "O". O script a seguir criará e salvará um gráfico de linha no diretório de trabalho R atual.
# Create the data for the chart.
v <- c(7,12,28,3,41)
# Give the chart file a name.
png(file = "line_chart.jpg")
# Plot the bar chart.
plot(v,type = "o")
# Save the file.
dev.off()Quando executamos o código acima, ele produz o seguinte resultado -
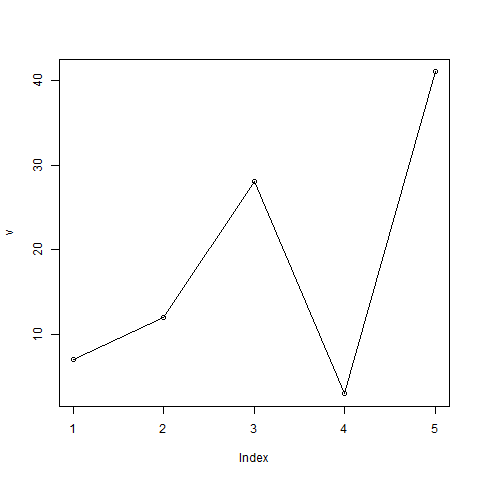
Título, cor e rótulos do gráfico de linha
Os recursos do gráfico de linha podem ser expandidos usando parâmetros adicionais. Adicionamos cor aos pontos e linhas, damos um título ao gráfico e adicionamos rótulos aos eixos.
Exemplo
# Create the data for the chart.
v <- c(7,12,28,3,41)
# Give the chart file a name.
png(file = "line_chart_label_colored.jpg")
# Plot the bar chart.
plot(v,type = "o", col = "red", xlab = "Month", ylab = "Rain fall",
main = "Rain fall chart")
# Save the file.
dev.off()Quando executamos o código acima, ele produz o seguinte resultado -
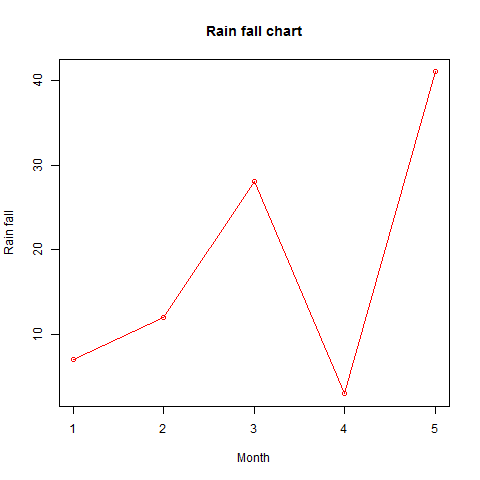
Várias linhas em um gráfico de linha
Mais de uma linha pode ser desenhada no mesmo gráfico usando o lines()função.
Depois que a primeira linha é plotada, a função lines () pode usar um vetor adicional como entrada para desenhar a segunda linha no gráfico,
# Create the data for the chart.
v <- c(7,12,28,3,41)
t <- c(14,7,6,19,3)
# Give the chart file a name.
png(file = "line_chart_2_lines.jpg")
# Plot the bar chart.
plot(v,type = "o",col = "red", xlab = "Month", ylab = "Rain fall",
main = "Rain fall chart")
lines(t, type = "o", col = "blue")
# Save the file.
dev.off()Quando executamos o código acima, ele produz o seguinte resultado -
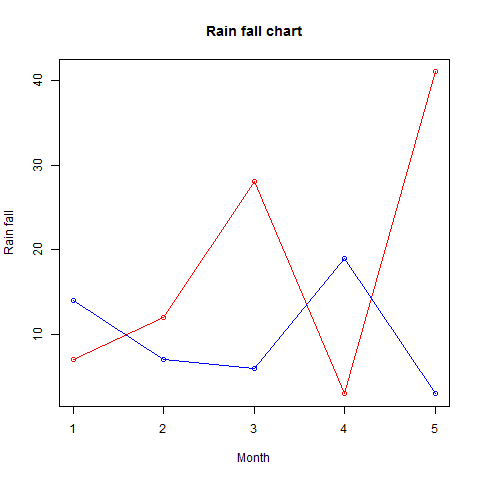
Os gráficos de dispersão mostram muitos pontos plotados no plano cartesiano. Cada ponto representa os valores de duas variáveis. Uma variável é escolhida no eixo horizontal e outra no eixo vertical.
O gráfico de dispersão simples é criado usando o plot() função.
Sintaxe
A sintaxe básica para a criação de gráfico de dispersão em R é -
plot(x, y, main, xlab, ylab, xlim, ylim, axes)A seguir está a descrição dos parâmetros usados -
x é o conjunto de dados cujos valores são as coordenadas horizontais.
y é o conjunto de dados cujos valores são as coordenadas verticais.
main é o bloco do gráfico.
xlab é o rótulo no eixo horizontal.
ylab é o rótulo no eixo vertical.
xlim são os limites dos valores de x usados para plotagem.
ylim são os limites dos valores de y usados para plotagem.
axes indica se ambos os eixos devem ser desenhados no gráfico.
Exemplo
Usamos o conjunto de dados "mtcars"disponível no ambiente R para criar um gráfico de dispersão básico. Vamos usar as colunas "wt" e "mpg" em mtcars.
input <- mtcars[,c('wt','mpg')]
print(head(input))Quando executamos o código acima, ele produz o seguinte resultado -
wt mpg
Mazda RX4 2.620 21.0
Mazda RX4 Wag 2.875 21.0
Datsun 710 2.320 22.8
Hornet 4 Drive 3.215 21.4
Hornet Sportabout 3.440 18.7
Valiant 3.460 18.1Criação do gráfico de dispersão
O script a seguir criará um gráfico de dispersão para a relação entre peso (peso) e mpg (milhas por galão).
# Get the input values.
input <- mtcars[,c('wt','mpg')]
# Give the chart file a name.
png(file = "scatterplot.png")
# Plot the chart for cars with weight between 2.5 to 5 and mileage between 15 and 30.
plot(x = input$wt,y = input$mpg,
xlab = "Weight",
ylab = "Milage",
xlim = c(2.5,5),
ylim = c(15,30),
main = "Weight vs Milage"
)
# Save the file.
dev.off()Quando executamos o código acima, ele produz o seguinte resultado -
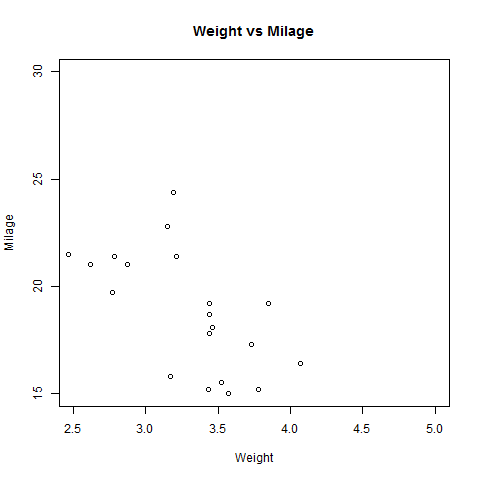
Matrizes de gráfico de dispersão
Quando temos mais de duas variáveis e queremos encontrar a correlação entre uma variável e as restantes, usamos a matriz de gráfico de dispersão. Nós usamospairs() função para criar matrizes de gráficos de dispersão.
Sintaxe
A sintaxe básica para a criação de matrizes de gráfico de dispersão em R é -
pairs(formula, data)A seguir está a descrição dos parâmetros usados -
formula representa a série de variáveis usadas em pares.
data representa o conjunto de dados do qual as variáveis serão obtidas.
Exemplo
Cada variável é pareada com cada uma das variáveis restantes. Um gráfico de dispersão é traçado para cada par.
# Give the chart file a name.
png(file = "scatterplot_matrices.png")
# Plot the matrices between 4 variables giving 12 plots.
# One variable with 3 others and total 4 variables.
pairs(~wt+mpg+disp+cyl,data = mtcars,
main = "Scatterplot Matrix")
# Save the file.
dev.off()Quando o código acima é executado, obtemos a seguinte saída.
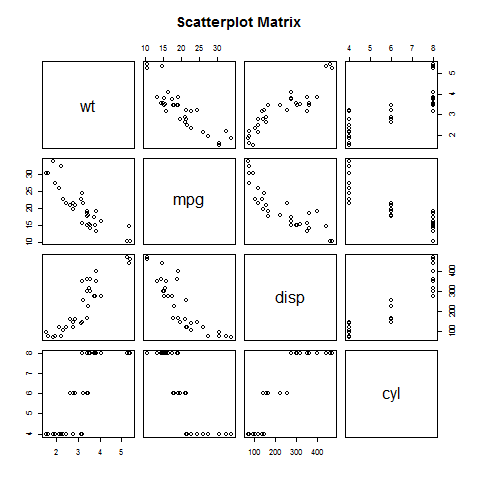
A análise estatística em R é realizada usando muitas funções embutidas. A maioria dessas funções faz parte do pacote R base. Essas funções tomam o vetor R como uma entrada junto com os argumentos e fornecem o resultado.
As funções que estamos discutindo neste capítulo são média, mediana e modo.
Significar
É calculado pegando a soma dos valores e dividindo com o número de valores em uma série de dados.
A função mean() é usado para calcular isso em R.
Sintaxe
A sintaxe básica para calcular a média em R é -
mean(x, trim = 0, na.rm = FALSE, ...)A seguir está a descrição dos parâmetros usados -
x é o vetor de entrada.
trim é usado para eliminar algumas observações de ambas as extremidades do vetor classificado.
na.rm é usado para remover os valores ausentes do vetor de entrada.
Exemplo
# Create a vector.
x <- c(12,7,3,4.2,18,2,54,-21,8,-5)
# Find Mean.
result.mean <- mean(x)
print(result.mean)Quando executamos o código acima, ele produz o seguinte resultado -
[1] 8.22Aplicando Opção de Corte
Quando o parâmetro trim é fornecido, os valores no vetor são classificados e, em seguida, os números necessários de observações são eliminados do cálculo da média.
Quando trim = 0,3, 3 valores de cada extremidade serão retirados dos cálculos para encontrar a média.
Neste caso, o vetor classificado é (−21, −5, 2, 3, 4,2, 7, 8, 12, 18, 54) e os valores removidos do vetor para calcular a média são (−21, −5,2) da esquerda e (12,18,54) da direita.
# Create a vector.
x <- c(12,7,3,4.2,18,2,54,-21,8,-5)
# Find Mean.
result.mean <- mean(x,trim = 0.3)
print(result.mean)Quando executamos o código acima, ele produz o seguinte resultado -
[1] 5.55Aplicando a Opção NA
Se houver valores ausentes, a função média retornará NA.
Para eliminar os valores ausentes do cálculo, use na.rm = TRUE. o que significa remover os valores NA.
# Create a vector.
x <- c(12,7,3,4.2,18,2,54,-21,8,-5,NA)
# Find mean.
result.mean <- mean(x)
print(result.mean)
# Find mean dropping NA values.
result.mean <- mean(x,na.rm = TRUE)
print(result.mean)Quando executamos o código acima, ele produz o seguinte resultado -
[1] NA
[1] 8.22Mediana
O valor mais intermediário em uma série de dados é chamado de mediana. omedian() função é usada em R para calcular este valor.
Sintaxe
A sintaxe básica para calcular a mediana em R é -
median(x, na.rm = FALSE)A seguir está a descrição dos parâmetros usados -
x é o vetor de entrada.
na.rm é usado para remover os valores ausentes do vetor de entrada.
Exemplo
# Create the vector.
x <- c(12,7,3,4.2,18,2,54,-21,8,-5)
# Find the median.
median.result <- median(x)
print(median.result)Quando executamos o código acima, ele produz o seguinte resultado -
[1] 5.6Modo
O modo é o valor que possui o maior número de ocorrências em um conjunto de dados. Ao contrário da média e da mediana, o modo pode ter dados numéricos e de caracteres.
R não tem uma função embutida padrão para calcular o modo. Portanto, criamos uma função de usuário para calcular o modo de um conjunto de dados em R. Essa função recebe o vetor como entrada e fornece o valor do modo como saída.
Exemplo
# Create the function.
getmode <- function(v) {
uniqv <- unique(v)
uniqv[which.max(tabulate(match(v, uniqv)))]
}
# Create the vector with numbers.
v <- c(2,1,2,3,1,2,3,4,1,5,5,3,2,3)
# Calculate the mode using the user function.
result <- getmode(v)
print(result)
# Create the vector with characters.
charv <- c("o","it","the","it","it")
# Calculate the mode using the user function.
result <- getmode(charv)
print(result)Quando executamos o código acima, ele produz o seguinte resultado -
[1] 2
[1] "it"A análise de regressão é uma ferramenta estatística amplamente utilizada para estabelecer um modelo de relacionamento entre duas variáveis. Uma dessas variáveis é chamada de variável preditora, cujo valor é obtido por meio de experimentos. A outra variável é chamada de variável de resposta, cujo valor é derivado da variável preditora.
Na regressão linear, essas duas variáveis são relacionadas por meio de uma equação, onde o expoente (potência) de ambas as variáveis é 1. Matematicamente, uma relação linear representa uma linha reta quando plotada como um gráfico. Uma relação não linear em que o expoente de qualquer variável não é igual a 1 cria uma curva.
A equação matemática geral para uma regressão linear é -
y = ax + bA seguir está a descrição dos parâmetros usados -
y é a variável de resposta.
x é a variável preditora.
a e b são constantes que são chamadas de coeficientes.
Passos para estabelecer uma regressão
Um exemplo simples de regressão é prever o peso de uma pessoa quando sua altura é conhecida. Para fazer isso, precisamos ter a relação entre altura e peso de uma pessoa.
As etapas para criar o relacionamento são -
Faça o experimento de coleta de uma amostra dos valores observados de altura e peso correspondente.
Crie um modelo de relacionamento usando o lm() funções em R.
Encontre os coeficientes do modelo criado e crie a equação matemática usando estes
Obtenha um resumo do modelo de relacionamento para saber o erro médio na previsão. Também chamadoresiduals.
Para prever o peso de novas pessoas, use o predict() função em R.
Dados de entrada
Abaixo estão os dados de amostra que representam as observações -
# Values of height
151, 174, 138, 186, 128, 136, 179, 163, 152, 131
# Values of weight.
63, 81, 56, 91, 47, 57, 76, 72, 62, 48Função lm ()
Esta função cria o modelo de relacionamento entre o preditor e a variável de resposta.
Sintaxe
A sintaxe básica para lm() função na regressão linear é -
lm(formula,data)A seguir está a descrição dos parâmetros usados -
formula é um símbolo que apresenta a relação entre x e y.
data é o vetor no qual a fórmula será aplicada.
Crie um modelo de relacionamento e obtenha os coeficientes
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
# Apply the lm() function.
relation <- lm(y~x)
print(relation)Quando executamos o código acima, ele produz o seguinte resultado -
Call:
lm(formula = y ~ x)
Coefficients:
(Intercept) x
-38.4551 0.6746Obtenha o Resumo do Relacionamento
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
# Apply the lm() function.
relation <- lm(y~x)
print(summary(relation))Quando executamos o código acima, ele produz o seguinte resultado -
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-6.3002 -1.6629 0.0412 1.8944 3.9775
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -38.45509 8.04901 -4.778 0.00139 **
x 0.67461 0.05191 12.997 1.16e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.253 on 8 degrees of freedom
Multiple R-squared: 0.9548, Adjusted R-squared: 0.9491
F-statistic: 168.9 on 1 and 8 DF, p-value: 1.164e-06Função Predict ()
Sintaxe
A sintaxe básica para predizer () em regressão linear é -
predict(object, newdata)A seguir está a descrição dos parâmetros usados -
object é a fórmula que já foi criada usando a função lm ().
newdata é o vetor que contém o novo valor da variável preditora.
Preveja o peso de novas pessoas
# The predictor vector.
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
# The resposne vector.
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
# Apply the lm() function.
relation <- lm(y~x)
# Find weight of a person with height 170.
a <- data.frame(x = 170)
result <- predict(relation,a)
print(result)Quando executamos o código acima, ele produz o seguinte resultado -
1
76.22869Visualize a regressão graficamente
# Create the predictor and response variable.
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
relation <- lm(y~x)
# Give the chart file a name.
png(file = "linearregression.png")
# Plot the chart.
plot(y,x,col = "blue",main = "Height & Weight Regression",
abline(lm(x~y)),cex = 1.3,pch = 16,xlab = "Weight in Kg",ylab = "Height in cm")
# Save the file.
dev.off()Quando executamos o código acima, ele produz o seguinte resultado -
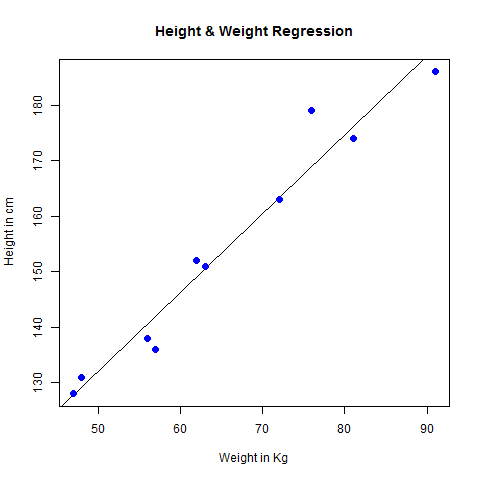
A regressão múltipla é uma extensão da regressão linear no relacionamento entre mais de duas variáveis. Na relação linear simples, temos um preditor e uma variável de resposta, mas na regressão múltipla temos mais de uma variável preditora e uma variável de resposta.
A equação matemática geral para regressão múltipla é -
y = a + b1x1 + b2x2 +...bnxnA seguir está a descrição dos parâmetros usados -
y é a variável de resposta.
a, b1, b2...bn são os coeficientes.
x1, x2, ...xn são as variáveis preditoras.
Criamos o modelo de regressão usando o lm()em R. O modelo determina o valor dos coeficientes usando os dados de entrada. Em seguida, podemos prever o valor da variável de resposta para um determinado conjunto de variáveis preditoras usando esses coeficientes.
Função lm ()
Esta função cria o modelo de relacionamento entre o preditor e a variável de resposta.
Sintaxe
A sintaxe básica para lm() função em regressão múltipla é -
lm(y ~ x1+x2+x3...,data)A seguir está a descrição dos parâmetros usados -
formula é um símbolo que apresenta a relação entre a variável de resposta e as variáveis preditoras.
data é o vetor no qual a fórmula será aplicada.
Exemplo
Dados de entrada
Considere o conjunto de dados "mtcars" disponível no ambiente R. Ele fornece uma comparação entre diferentes modelos de carros em termos de quilometragem por galão (mpg), deslocamento do cilindro ("disp"), cavalos de força ("hp"), peso do carro ("wt") e mais alguns parâmetros.
O objetivo do modelo é estabelecer a relação entre "mpg" como uma variável de resposta com "disp", "hp" e "wt" como variáveis preditoras. Criamos um subconjunto dessas variáveis a partir do conjunto de dados mtcars para esse propósito.
input <- mtcars[,c("mpg","disp","hp","wt")]
print(head(input))Quando executamos o código acima, ele produz o seguinte resultado -
mpg disp hp wt
Mazda RX4 21.0 160 110 2.620
Mazda RX4 Wag 21.0 160 110 2.875
Datsun 710 22.8 108 93 2.320
Hornet 4 Drive 21.4 258 110 3.215
Hornet Sportabout 18.7 360 175 3.440
Valiant 18.1 225 105 3.460Crie um modelo de relacionamento e obtenha os coeficientes
input <- mtcars[,c("mpg","disp","hp","wt")]
# Create the relationship model.
model <- lm(mpg~disp+hp+wt, data = input)
# Show the model.
print(model)
# Get the Intercept and coefficients as vector elements.
cat("# # # # The Coefficient Values # # # ","\n")
a <- coef(model)[1]
print(a)
Xdisp <- coef(model)[2]
Xhp <- coef(model)[3]
Xwt <- coef(model)[4]
print(Xdisp)
print(Xhp)
print(Xwt)Quando executamos o código acima, ele produz o seguinte resultado -
Call:
lm(formula = mpg ~ disp + hp + wt, data = input)
Coefficients:
(Intercept) disp hp wt
37.105505 -0.000937 -0.031157 -3.800891
# # # # The Coefficient Values # # #
(Intercept)
37.10551
disp
-0.0009370091
hp
-0.03115655
wt
-3.800891Criar Equação para Modelo de Regressão
Com base nos valores de interceptação e coeficiente acima, criamos a equação matemática.
Y = a+Xdisp.x1+Xhp.x2+Xwt.x3
or
Y = 37.15+(-0.000937)*x1+(-0.0311)*x2+(-3.8008)*x3Aplicar equação para prever novos valores
Podemos usar a equação de regressão criada acima para prever a quilometragem quando um novo conjunto de valores para deslocamento, cavalos de potência e peso é fornecido.
Para um carro com disp = 221, hp = 102 e wt = 2,91, a quilometragem prevista é -
Y = 37.15+(-0.000937)*221+(-0.0311)*102+(-3.8008)*2.91 = 22.7104A Regressão Logística é um modelo de regressão no qual a variável de resposta (variável dependente) possui valores categóricos, como Verdadeiro / Falso ou 0/1. Na verdade, mede a probabilidade de uma resposta binária como o valor da variável de resposta com base na equação matemática relacionando-a com as variáveis preditoras.
A equação matemática geral para regressão logística é -
y = 1/(1+e^-(a+b1x1+b2x2+b3x3+...))A seguir está a descrição dos parâmetros usados -
y é a variável de resposta.
x é a variável preditora.
a e b são os coeficientes que são constantes numéricas.
A função usada para criar o modelo de regressão é o glm() função.
Sintaxe
A sintaxe básica para glm() função na regressão logística é -
glm(formula,data,family)A seguir está a descrição dos parâmetros usados -
formula é o símbolo que apresenta a relação entre as variáveis.
data é o conjunto de dados que fornece os valores dessas variáveis.
familyé o objeto R para especificar os detalhes do modelo. Seu valor é binomial para regressão logística.
Exemplo
O conjunto de dados integrado "mtcars" descreve diferentes modelos de um carro com suas várias especificações de motor. No conjunto de dados "mtcars", o modo de transmissão (automático ou manual) é descrito pela coluna am, que é um valor binário (0 ou 1). Podemos criar um modelo de regressão logística entre as colunas "am" e 3 outras colunas - hp, wt e cyl.
# Select some columns form mtcars.
input <- mtcars[,c("am","cyl","hp","wt")]
print(head(input))Quando executamos o código acima, ele produz o seguinte resultado -
am cyl hp wt
Mazda RX4 1 6 110 2.620
Mazda RX4 Wag 1 6 110 2.875
Datsun 710 1 4 93 2.320
Hornet 4 Drive 0 6 110 3.215
Hornet Sportabout 0 8 175 3.440
Valiant 0 6 105 3.460Criar modelo de regressão
Nós usamos o glm() função para criar o modelo de regressão e obter seu resumo para análise.
input <- mtcars[,c("am","cyl","hp","wt")]
am.data = glm(formula = am ~ cyl + hp + wt, data = input, family = binomial)
print(summary(am.data))Quando executamos o código acima, ele produz o seguinte resultado -
Call:
glm(formula = am ~ cyl + hp + wt, family = binomial, data = input)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.17272 -0.14907 -0.01464 0.14116 1.27641
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 19.70288 8.11637 2.428 0.0152 *
cyl 0.48760 1.07162 0.455 0.6491
hp 0.03259 0.01886 1.728 0.0840 .
wt -9.14947 4.15332 -2.203 0.0276 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 43.2297 on 31 degrees of freedom
Residual deviance: 9.8415 on 28 degrees of freedom
AIC: 17.841
Number of Fisher Scoring iterations: 8Conclusão
No resumo, como o valor de p na última coluna é maior que 0,05 para as variáveis "cil" e "hp", consideramos que são insignificantes na contribuição para o valor da variável "am". Apenas o peso (peso) impacta o valor "am" neste modelo de regressão.
Em uma coleta aleatória de dados de fontes independentes, geralmente observa-se que a distribuição dos dados é normal. Ou seja, ao traçar um gráfico com o valor da variável no eixo horizontal e a contagem dos valores no eixo vertical, obtemos uma curva em forma de sino. O centro da curva representa a média do conjunto de dados. No gráfico, cinquenta por cento dos valores ficam à esquerda da média e os outros cinquenta por cento ficam à direita do gráfico. Isso é conhecido como distribuição normal nas estatísticas.
R tem quatro funções integradas para gerar distribuição normal. Eles são descritos a seguir.
dnorm(x, mean, sd)
pnorm(x, mean, sd)
qnorm(p, mean, sd)
rnorm(n, mean, sd)A seguir está a descrição dos parâmetros usados nas funções acima -
x é um vetor de números.
p é um vetor de probabilidades.
n é o número de observações (tamanho da amostra).
meané o valor médio dos dados da amostra. Seu valor padrão é zero.
sdé o desvio padrão. Seu valor padrão é 1.
dnorm ()
Esta função fornece a altura da distribuição de probabilidade em cada ponto para uma determinada média e desvio padrão.
# Create a sequence of numbers between -10 and 10 incrementing by 0.1.
x <- seq(-10, 10, by = .1)
# Choose the mean as 2.5 and standard deviation as 0.5.
y <- dnorm(x, mean = 2.5, sd = 0.5)
# Give the chart file a name.
png(file = "dnorm.png")
plot(x,y)
# Save the file.
dev.off()Quando executamos o código acima, ele produz o seguinte resultado -
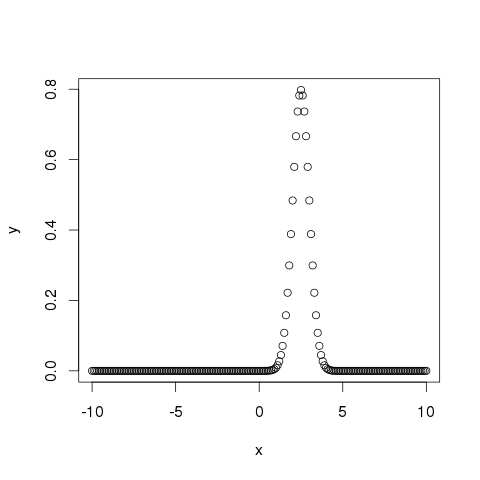
pnorm ()
Essa função fornece a probabilidade de um número aleatório normalmente distribuído ser menor que o valor de um determinado número. Também é chamada de "Função de distribuição cumulativa".
# Create a sequence of numbers between -10 and 10 incrementing by 0.2.
x <- seq(-10,10,by = .2)
# Choose the mean as 2.5 and standard deviation as 2.
y <- pnorm(x, mean = 2.5, sd = 2)
# Give the chart file a name.
png(file = "pnorm.png")
# Plot the graph.
plot(x,y)
# Save the file.
dev.off()Quando executamos o código acima, ele produz o seguinte resultado -
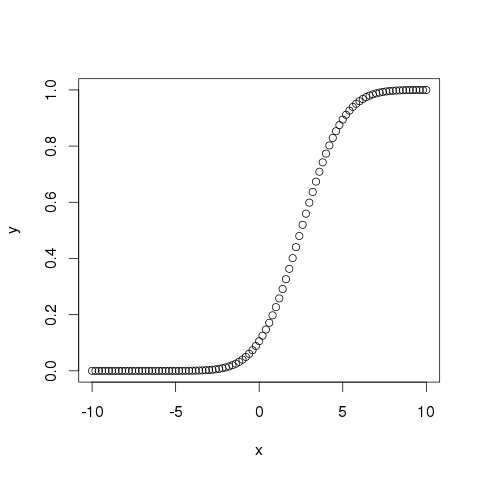
qnorm ()
Esta função obtém o valor da probabilidade e fornece um número cujo valor cumulativo corresponde ao valor da probabilidade.
# Create a sequence of probability values incrementing by 0.02.
x <- seq(0, 1, by = 0.02)
# Choose the mean as 2 and standard deviation as 3.
y <- qnorm(x, mean = 2, sd = 1)
# Give the chart file a name.
png(file = "qnorm.png")
# Plot the graph.
plot(x,y)
# Save the file.
dev.off()Quando executamos o código acima, ele produz o seguinte resultado -
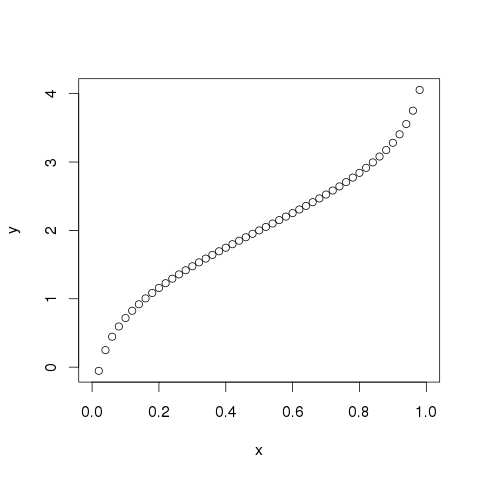
rnorm ()
Esta função é usada para gerar números aleatórios cuja distribuição é normal. Ele pega o tamanho da amostra como entrada e gera muitos números aleatórios. Desenhamos um histograma para mostrar a distribuição dos números gerados.
# Create a sample of 50 numbers which are normally distributed.
y <- rnorm(50)
# Give the chart file a name.
png(file = "rnorm.png")
# Plot the histogram for this sample.
hist(y, main = "Normal DIstribution")
# Save the file.
dev.off()Quando executamos o código acima, ele produz o seguinte resultado -
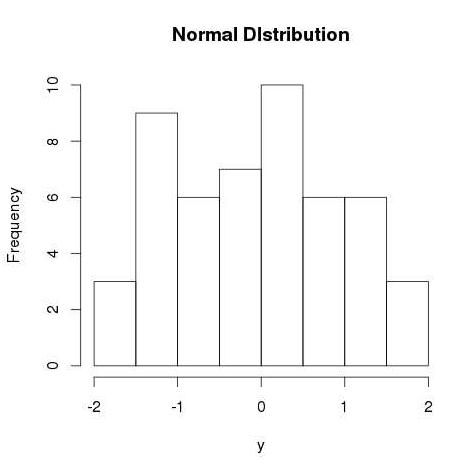
O modelo de distribuição binomial trata de encontrar a probabilidade de sucesso de um evento que tem apenas dois resultados possíveis em uma série de experimentos. Por exemplo, o lançamento de uma moeda sempre dá cara ou coroa. A probabilidade de encontrar exatamente 3 caras ao jogar uma moeda repetidamente por 10 vezes é estimada durante a distribuição binomial.
R tem quatro funções embutidas para gerar distribuição binomial. Eles são descritos a seguir.
dbinom(x, size, prob)
pbinom(x, size, prob)
qbinom(p, size, prob)
rbinom(n, size, prob)A seguir está a descrição dos parâmetros usados -
x é um vetor de números.
p é um vetor de probabilidades.
n é o número de observações.
size é o número de tentativas.
prob é a probabilidade de sucesso de cada tentativa.
dbinom ()
Esta função fornece a distribuição de densidade de probabilidade em cada ponto.
# Create a sample of 50 numbers which are incremented by 1.
x <- seq(0,50,by = 1)
# Create the binomial distribution.
y <- dbinom(x,50,0.5)
# Give the chart file a name.
png(file = "dbinom.png")
# Plot the graph for this sample.
plot(x,y)
# Save the file.
dev.off()Quando executamos o código acima, ele produz o seguinte resultado -
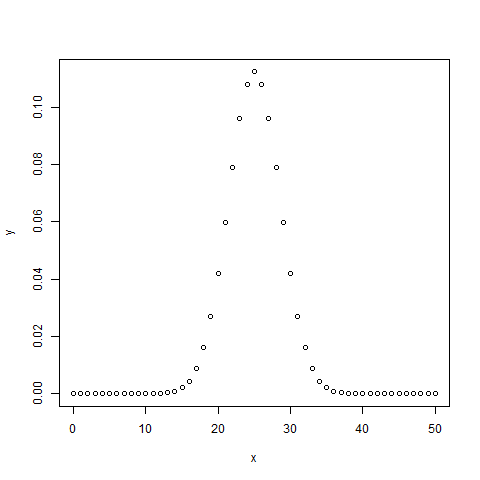
pbinom ()
Esta função fornece a probabilidade cumulativa de um evento. É um único valor que representa a probabilidade.
# Probability of getting 26 or less heads from a 51 tosses of a coin.
x <- pbinom(26,51,0.5)
print(x)Quando executamos o código acima, ele produz o seguinte resultado -
[1] 0.610116qbinom ()
Esta função obtém o valor da probabilidade e fornece um número cujo valor cumulativo corresponde ao valor da probabilidade.
# How many heads will have a probability of 0.25 will come out when a coin
# is tossed 51 times.
x <- qbinom(0.25,51,1/2)
print(x)Quando executamos o código acima, ele produz o seguinte resultado -
[1] 23rbinom ()
Essa função gera o número necessário de valores aleatórios de determinada probabilidade de uma determinada amostra.
# Find 8 random values from a sample of 150 with probability of 0.4.
x <- rbinom(8,150,.4)
print(x)Quando executamos o código acima, ele produz o seguinte resultado -
[1] 58 61 59 66 55 60 61 67A regressão de Poisson envolve modelos de regressão nos quais a variável de resposta está na forma de contagens e não de números fracionários. Por exemplo, a contagem do número de nascimentos ou de vitórias em uma série de partidas de futebol. Além disso, os valores das variáveis de resposta seguem uma distribuição de Poisson.
A equação matemática geral para regressão de Poisson é -
log(y) = a + b1x1 + b2x2 + bnxn.....A seguir está a descrição dos parâmetros usados -
y é a variável de resposta.
a e b são os coeficientes numéricos.
x é a variável preditora.
A função usada para criar o modelo de regressão de Poisson é o glm() função.
Sintaxe
A sintaxe básica para glm() função na regressão de Poisson é -
glm(formula,data,family)A seguir está a descrição dos parâmetros usados nas funções acima -
formula é o símbolo que apresenta a relação entre as variáveis.
data é o conjunto de dados que fornece os valores dessas variáveis.
familyé o objeto R para especificar os detalhes do modelo. Seu valor é 'Poisson' para Regressão Logística.
Exemplo
Temos o conjunto de dados embutido "quebra de urdidura" que descreve o efeito do tipo de lã (A ou B) e tensão (baixa, média ou alta) no número de quebras de urdidura por tear. Vamos considerar "quebras" como a variável de resposta que é uma contagem do número de quebras. O "tipo" e a "tensão" da lã são considerados variáveis de previsão.
Input Data
input <- warpbreaks
print(head(input))Quando executamos o código acima, ele produz o seguinte resultado -
breaks wool tension
1 26 A L
2 30 A L
3 54 A L
4 25 A L
5 70 A L
6 52 A LCriar modelo de regressão
output <-glm(formula = breaks ~ wool+tension, data = warpbreaks,
family = poisson)
print(summary(output))Quando executamos o código acima, ele produz o seguinte resultado -
Call:
glm(formula = breaks ~ wool + tension, family = poisson, data = warpbreaks)
Deviance Residuals:
Min 1Q Median 3Q Max
-3.6871 -1.6503 -0.4269 1.1902 4.2616
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 3.69196 0.04541 81.302 < 2e-16 ***
woolB -0.20599 0.05157 -3.994 6.49e-05 ***
tensionM -0.32132 0.06027 -5.332 9.73e-08 ***
tensionH -0.51849 0.06396 -8.107 5.21e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 297.37 on 53 degrees of freedom
Residual deviance: 210.39 on 50 degrees of freedom
AIC: 493.06
Number of Fisher Scoring iterations: 4No resumo, procuramos que o valor p na última coluna seja inferior a 0,05 para considerar um impacto da variável preditora na variável de resposta. Como visto, o tipo lã B com tensão do tipo M e H tem impacto na contagem de quebras.
Usamos a análise de regressão para criar modelos que descrevem o efeito da variação nas variáveis preditoras na variável de resposta. Às vezes, se tivermos uma variável categórica com valores como Sim / Não ou Masculino / Feminino etc. A análise de regressão simples fornece vários resultados para cada valor da variável categórica. Nesse cenário, podemos estudar o efeito da variável categórica usando-a junto com a variável preditora e comparando as linhas de regressão para cada nível da variável categórica. Essa análise é denominada comoAnalysis of Covariance também chamado de ANCOVA.
Exemplo
Considere o R construído em mtcars de conjunto de dados. Nele observamos que o campo "am" representa o tipo de transmissão (automática ou manual). É uma variável categórica com valores 0 e 1. O valor de milhas por galão (mpg) de um carro também pode depender dele além do valor dos cavalos de força ("hp").
Estudamos o efeito do valor de "am" na regressão entre "mpg" e "hp". Isso é feito usando oaov() função seguida por anova() função para comparar as regressões múltiplas.
Dados de entrada
Crie um quadro de dados contendo os campos "mpg", "hp" e "am" do conjunto de dados mtcars. Aqui, consideramos "mpg" como a variável de resposta, "hp" como a variável preditora e "am" como a variável categórica.
input <- mtcars[,c("am","mpg","hp")]
print(head(input))Quando executamos o código acima, ele produz o seguinte resultado -
am mpg hp
Mazda RX4 1 21.0 110
Mazda RX4 Wag 1 21.0 110
Datsun 710 1 22.8 93
Hornet 4 Drive 0 21.4 110
Hornet Sportabout 0 18.7 175
Valiant 0 18.1 105Análise ANCOVA
Criamos um modelo de regressão tendo "hp" como variável preditora e "mpg" como variável de resposta levando em consideração a interação entre "am" e "hp".
Modelo com interação entre variável categórica e variável preditora
# Get the dataset.
input <- mtcars
# Create the regression model.
result <- aov(mpg~hp*am,data = input)
print(summary(result))Quando executamos o código acima, ele produz o seguinte resultado -
Df Sum Sq Mean Sq F value Pr(>F)
hp 1 678.4 678.4 77.391 1.50e-09 ***
am 1 202.2 202.2 23.072 4.75e-05 ***
hp:am 1 0.0 0.0 0.001 0.981
Residuals 28 245.4 8.8
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Este resultado mostra que os cavalos de potência e o tipo de transmissão têm efeito significativo nas milhas por galão, pois o valor de p em ambos os casos é inferior a 0,05. Mas a interação entre essas duas variáveis não é significativa, pois o valor p é maior que 0,05.
Modelo sem interação entre variável categórica e variável preditora
# Get the dataset.
input <- mtcars
# Create the regression model.
result <- aov(mpg~hp+am,data = input)
print(summary(result))Quando executamos o código acima, ele produz o seguinte resultado -
Df Sum Sq Mean Sq F value Pr(>F)
hp 1 678.4 678.4 80.15 7.63e-10 ***
am 1 202.2 202.2 23.89 3.46e-05 ***
Residuals 29 245.4 8.5
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Este resultado mostra que os cavalos de potência e o tipo de transmissão têm efeito significativo nas milhas por galão, pois o valor de p em ambos os casos é inferior a 0,05.
Comparando Dois Modelos
Agora podemos comparar os dois modelos para concluir se a interação das variáveis é realmente in-significativa. Para isso usamos oanova() função.
# Get the dataset.
input <- mtcars
# Create the regression models.
result1 <- aov(mpg~hp*am,data = input)
result2 <- aov(mpg~hp+am,data = input)
# Compare the two models.
print(anova(result1,result2))Quando executamos o código acima, ele produz o seguinte resultado -
Model 1: mpg ~ hp * am
Model 2: mpg ~ hp + am
Res.Df RSS Df Sum of Sq F Pr(>F)
1 28 245.43
2 29 245.44 -1 -0.0052515 6e-04 0.9806Como o valor p é maior que 0,05, concluímos que a interação entre os cavalos de potência e o tipo de transmissão não é significativa. Portanto, a quilometragem por galão dependerá de maneira semelhante dos cavalos de potência do carro, tanto no modo de transmissão automática quanto manual.
A série temporal é uma série de pontos de dados em que cada ponto de dados está associado a um carimbo de data / hora. Um exemplo simples é o preço de uma ação no mercado de ações em diferentes pontos do tempo em um determinado dia. Outro exemplo é a quantidade de chuvas em uma região em diferentes meses do ano. A linguagem R usa muitas funções para criar, manipular e plotar os dados da série temporal. Os dados da série temporal são armazenados em um objeto R chamadotime-series object. Também é um objeto de dados R como um vetor ou quadro de dados.
O objeto de série temporal é criado usando o ts() função.
Sintaxe
A sintaxe básica para ts() função na análise de série temporal é -
timeseries.object.name <- ts(data, start, end, frequency)A seguir está a descrição dos parâmetros usados -
data é um vetor ou matriz que contém os valores usados na série temporal.
start especifica a hora de início da primeira observação na série temporal.
end especifica a hora de término da última observação na série temporal.
frequency especifica o número de observações por unidade de tempo.
Exceto o parâmetro "dados", todos os outros parâmetros são opcionais.
Exemplo
Considere os detalhes da precipitação anual em um local a partir de janeiro de 2012. Criamos um objeto de série temporal R por um período de 12 meses e o plotamos.
# Get the data points in form of a R vector.
rainfall <- c(799,1174.8,865.1,1334.6,635.4,918.5,685.5,998.6,784.2,985,882.8,1071)
# Convert it to a time series object.
rainfall.timeseries <- ts(rainfall,start = c(2012,1),frequency = 12)
# Print the timeseries data.
print(rainfall.timeseries)
# Give the chart file a name.
png(file = "rainfall.png")
# Plot a graph of the time series.
plot(rainfall.timeseries)
# Save the file.
dev.off()Quando executamos o código acima, ele produz o seguinte resultado e gráfico -
Jan Feb Mar Apr May Jun Jul Aug Sep
2012 799.0 1174.8 865.1 1334.6 635.4 918.5 685.5 998.6 784.2
Oct Nov Dec
2012 985.0 882.8 1071.0O gráfico de série temporal -
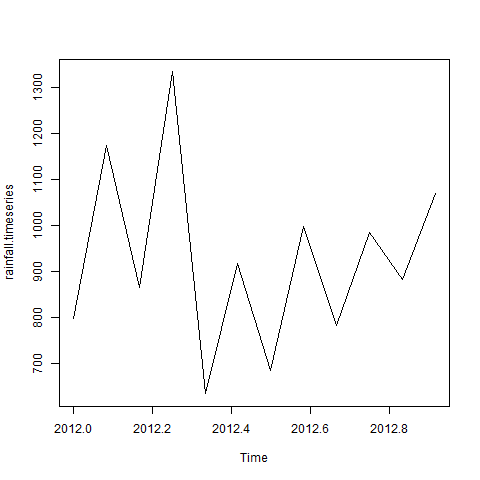
Diferentes intervalos de tempo
O valor do frequencyparâmetro na função ts () decide os intervalos de tempo nos quais os pontos de dados são medidos. Um valor de 12 indica que a série temporal é de 12 meses. Outros valores e seu significado são os seguintes -
frequency = 12 rastreia os pontos de dados para cada mês do ano.
frequency = 4 rastreia os pontos de dados para cada trimestre de um ano.
frequency = 6 rastreia os pontos de dados a cada 10 minutos de uma hora.
frequency = 24*6 rastreia os pontos de dados a cada 10 minutos de um dia.
Várias Séries Temporais
Podemos plotar várias séries temporais em um gráfico, combinando ambas as séries em uma matriz.
# Get the data points in form of a R vector.
rainfall1 <- c(799,1174.8,865.1,1334.6,635.4,918.5,685.5,998.6,784.2,985,882.8,1071)
rainfall2 <-
c(655,1306.9,1323.4,1172.2,562.2,824,822.4,1265.5,799.6,1105.6,1106.7,1337.8)
# Convert them to a matrix.
combined.rainfall <- matrix(c(rainfall1,rainfall2),nrow = 12)
# Convert it to a time series object.
rainfall.timeseries <- ts(combined.rainfall,start = c(2012,1),frequency = 12)
# Print the timeseries data.
print(rainfall.timeseries)
# Give the chart file a name.
png(file = "rainfall_combined.png")
# Plot a graph of the time series.
plot(rainfall.timeseries, main = "Multiple Time Series")
# Save the file.
dev.off()Quando executamos o código acima, ele produz o seguinte resultado e gráfico -
Series 1 Series 2
Jan 2012 799.0 655.0
Feb 2012 1174.8 1306.9
Mar 2012 865.1 1323.4
Apr 2012 1334.6 1172.2
May 2012 635.4 562.2
Jun 2012 918.5 824.0
Jul 2012 685.5 822.4
Aug 2012 998.6 1265.5
Sep 2012 784.2 799.6
Oct 2012 985.0 1105.6
Nov 2012 882.8 1106.7
Dec 2012 1071.0 1337.8O gráfico de várias séries temporais -
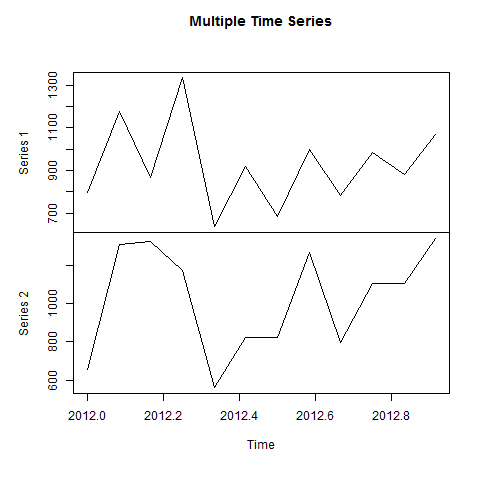
Ao modelar dados do mundo real para análise de regressão, observamos que raramente é o caso em que a equação do modelo é uma equação linear fornecendo um gráfico linear. Na maioria das vezes, a equação do modelo de dados do mundo real envolve funções matemáticas de alto grau, como um expoente de 3 ou uma função de pecado. Nesse cenário, o gráfico do modelo fornece uma curva em vez de uma linha. O objetivo da regressão linear e não linear é ajustar os valores dos parâmetros do modelo para encontrar a linha ou curva que mais se aproxima de seus dados. Ao encontrar esses valores, seremos capazes de estimar a variável de resposta com boa precisão.
Na regressão de Mínimos Quadrados, estabelecemos um modelo de regressão no qual a soma dos quadrados das distâncias verticais de diferentes pontos da curva de regressão é minimizada. Geralmente começamos com um modelo definido e assumimos alguns valores para os coeficientes. Em seguida, aplicamos onls() função de R para obter os valores mais precisos junto com os intervalos de confiança.
Sintaxe
A sintaxe básica para criar um teste de mínimos quadrados não linear em R é -
nls(formula, data, start)A seguir está a descrição dos parâmetros usados -
formula é uma fórmula de modelo não linear que inclui variáveis e parâmetros.
data é um quadro de dados usado para avaliar as variáveis na fórmula.
start é uma lista nomeada ou vetor numérico nomeado de estimativas iniciais.
Exemplo
Vamos considerar um modelo não linear com suposição de valores iniciais de seus coeficientes. A seguir, veremos quais são os intervalos de confiança desses valores assumidos para que possamos avaliar o quão bem esses valores se encaixam no modelo.
Então, vamos considerar a equação abaixo para este propósito -
a = b1*x^2+b2Vamos supor que os coeficientes iniciais sejam 1 e 3 e ajustar esses valores na função nls ().
xvalues <- c(1.6,2.1,2,2.23,3.71,3.25,3.4,3.86,1.19,2.21)
yvalues <- c(5.19,7.43,6.94,8.11,18.75,14.88,16.06,19.12,3.21,7.58)
# Give the chart file a name.
png(file = "nls.png")
# Plot these values.
plot(xvalues,yvalues)
# Take the assumed values and fit into the model.
model <- nls(yvalues ~ b1*xvalues^2+b2,start = list(b1 = 1,b2 = 3))
# Plot the chart with new data by fitting it to a prediction from 100 data points.
new.data <- data.frame(xvalues = seq(min(xvalues),max(xvalues),len = 100))
lines(new.data$xvalues,predict(model,newdata = new.data))
# Save the file.
dev.off()
# Get the sum of the squared residuals.
print(sum(resid(model)^2))
# Get the confidence intervals on the chosen values of the coefficients.
print(confint(model))Quando executamos o código acima, ele produz o seguinte resultado -
[1] 1.081935
Waiting for profiling to be done...
2.5% 97.5%
b1 1.137708 1.253135
b2 1.497364 2.496484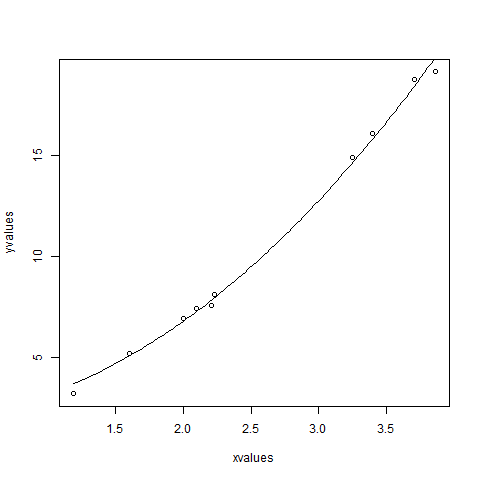
Podemos concluir que o valor de b1 está mais próximo de 1 enquanto o valor de b2 está mais próximo de 2 e não de 3.
A árvore de decisão é um gráfico que representa as escolhas e seus resultados na forma de uma árvore. Os nós no gráfico representam um evento ou escolha e as arestas do gráfico representam as regras ou condições de decisão. É usado principalmente em aplicativos de aprendizado de máquina e mineração de dados usando R.
Exemplos de uso de tress de decisão são - prever um email como spam ou não spam, prever que um tumor é canceroso ou prever um empréstimo como um risco de crédito bom ou ruim com base nos fatores de cada um deles. Geralmente, um modelo é criado com dados observados, também chamados de dados de treinamento. Em seguida, um conjunto de dados de validação é usado para verificar e melhorar o modelo. R tem pacotes que são usados para criar e visualizar árvores de decisão. Para um novo conjunto de variável preditora, usamos este modelo para chegar a uma decisão sobre a categoria (sim / Não, spam / não spam) dos dados.
O pacote R "party" é usado para criar árvores de decisão.
Instale o pacote R
Use o comando abaixo no console R para instalar o pacote. Você também deve instalar os pacotes dependentes, se houver.
install.packages("party")O pacote "festa" tem a função ctree() que é usado para criar e analisar a árvore de decisão.
Sintaxe
A sintaxe básica para criar uma árvore de decisão em R é -
ctree(formula, data)A seguir está a descrição dos parâmetros usados -
formula é uma fórmula que descreve o preditor e as variáveis de resposta.
data é o nome do conjunto de dados usado.
Dados de entrada
Usaremos o conjunto de dados embutido do R denominado readingSkillspara criar uma árvore de decisão. Descreve a pontuação das habilidades de leitura de alguém se conhecermos as variáveis "idade", "tamanho do calçado", "pontuação" e se a pessoa é falante nativo ou não.
Aqui estão os dados de amostra.
# Load the party package. It will automatically load other
# dependent packages.
library(party)
# Print some records from data set readingSkills.
print(head(readingSkills))Quando executamos o código acima, ele produz o seguinte resultado e gráfico -
nativeSpeaker age shoeSize score
1 yes 5 24.83189 32.29385
2 yes 6 25.95238 36.63105
3 no 11 30.42170 49.60593
4 yes 7 28.66450 40.28456
5 yes 11 31.88207 55.46085
6 yes 10 30.07843 52.83124
Loading required package: methods
Loading required package: grid
...............................
...............................Exemplo
Vamos usar o ctree() função para criar a árvore de decisão e ver seu gráfico.
# Load the party package. It will automatically load other
# dependent packages.
library(party)
# Create the input data frame.
input.dat <- readingSkills[c(1:105),]
# Give the chart file a name.
png(file = "decision_tree.png")
# Create the tree.
output.tree <- ctree(
nativeSpeaker ~ age + shoeSize + score,
data = input.dat)
# Plot the tree.
plot(output.tree)
# Save the file.
dev.off()Quando executamos o código acima, ele produz o seguinte resultado -
null device
1
Loading required package: methods
Loading required package: grid
Loading required package: mvtnorm
Loading required package: modeltools
Loading required package: stats4
Loading required package: strucchange
Loading required package: zoo
Attaching package: ‘zoo’
The following objects are masked from ‘package:base’:
as.Date, as.Date.numeric
Loading required package: sandwich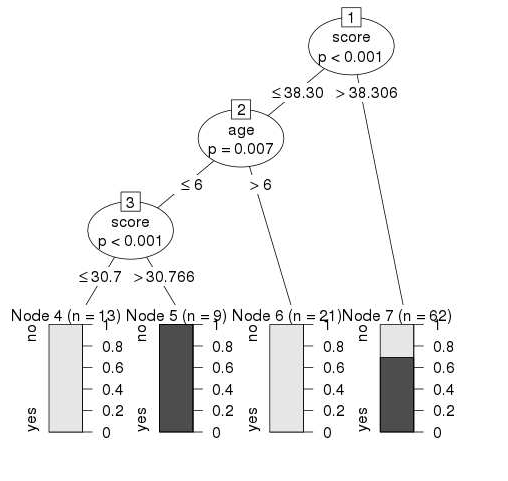
Conclusão
A partir da árvore de decisão mostrada acima, podemos concluir que qualquer pessoa cuja pontuação em habilidades de leitura seja inferior a 38,3 e a idade seja superior a 6 não é um falante nativo.
Na abordagem de floresta aleatória, um grande número de árvores de decisão é criado. Cada observação é inserida em cada árvore de decisão. O resultado mais comum para cada observação é usado como resultado final. Uma nova observação é inserida em todas as árvores e obtendo uma votação majoritária para cada modelo de classificação.
Uma estimativa de erro é feita para os casos que não foram usados durante a construção da árvore. Isso é chamado deOOB (Out-of-bag) estimativa de erro que é mencionada como uma porcentagem.
O pacote R "randomForest" é usado para criar florestas aleatórias.
Instale o pacote R
Use o comando abaixo no console R para instalar o pacote. Você também deve instalar os pacotes dependentes, se houver.
install.packages("randomForest)O pacote "randomForest" tem a função randomForest() que é usado para criar e analisar florestas aleatórias.
Sintaxe
A sintaxe básica para criar uma floresta aleatória em R é -
randomForest(formula, data)A seguir está a descrição dos parâmetros usados -
formula é uma fórmula que descreve o preditor e as variáveis de resposta.
data é o nome do conjunto de dados usado.
Dados de entrada
Usaremos o conjunto de dados embutido do R denominado readingSkills para criar uma árvore de decisão. Descreve a pontuação das habilidades de leitura de alguém se conhecermos as variáveis "idade", "tamanho do calçado", "pontuação" e se a pessoa é falante nativo.
Aqui estão os dados de amostra.
# Load the party package. It will automatically load other
# required packages.
library(party)
# Print some records from data set readingSkills.
print(head(readingSkills))Quando executamos o código acima, ele produz o seguinte resultado e gráfico -
nativeSpeaker age shoeSize score
1 yes 5 24.83189 32.29385
2 yes 6 25.95238 36.63105
3 no 11 30.42170 49.60593
4 yes 7 28.66450 40.28456
5 yes 11 31.88207 55.46085
6 yes 10 30.07843 52.83124
Loading required package: methods
Loading required package: grid
...............................
...............................Exemplo
Vamos usar o randomForest() função para criar a árvore de decisão e ver seu gráfico.
# Load the party package. It will automatically load other
# required packages.
library(party)
library(randomForest)
# Create the forest.
output.forest <- randomForest(nativeSpeaker ~ age + shoeSize + score,
data = readingSkills)
# View the forest results.
print(output.forest)
# Importance of each predictor.
print(importance(fit,type = 2))Quando executamos o código acima, ele produz o seguinte resultado -
Call:
randomForest(formula = nativeSpeaker ~ age + shoeSize + score,
data = readingSkills)
Type of random forest: classification
Number of trees: 500
No. of variables tried at each split: 1
OOB estimate of error rate: 1%
Confusion matrix:
no yes class.error
no 99 1 0.01
yes 1 99 0.01
MeanDecreaseGini
age 13.95406
shoeSize 18.91006
score 56.73051Conclusão
Da floresta aleatória mostrada acima, podemos concluir que o tamanho do calçado e a pontuação são os fatores importantes para decidir se alguém é falante nativo ou não. Além disso, o modelo tem apenas 1% de erro, o que significa que podemos prever com 99% de precisão.
A análise de sobrevivência trata de prever o momento em que um evento específico irá ocorrer. Também é conhecido como análise do tempo de falha ou análise do tempo até a morte. Por exemplo, prever o número de dias que uma pessoa com câncer sobreviverá ou quando um sistema mecânico irá falhar.
O pacote R denominado survivalé usado para realizar análises de sobrevivência. Este pacote contém a funçãoSurv()que pega os dados de entrada como uma fórmula R e cria um objeto de sobrevivência entre as variáveis escolhidas para análise. Então usamos a funçãosurvfit() para criar um gráfico para a análise.
Pacote de instalação
install.packages("survival")Sintaxe
A sintaxe básica para a criação de análise de sobrevivência em R é -
Surv(time,event)
survfit(formula)A seguir está a descrição dos parâmetros usados -
time é o tempo de acompanhamento até que o evento ocorra.
event indica o status de ocorrência do evento esperado.
formula é a relação entre as variáveis preditoras.
Exemplo
Vamos considerar o conjunto de dados denominado "pbc" presente nos pacotes de sobrevivência instalados acima. Ele descreve os pontos de dados de sobrevivência sobre pessoas afetadas com cirrose biliar primária (PBC) do fígado. Entre as muitas colunas presentes no conjunto de dados, estamos principalmente preocupados com os campos "hora" e "status". O tempo representa o número de dias entre o registro do paciente e antes do evento entre o paciente que recebe um transplante de fígado ou a morte do paciente.
# Load the library.
library("survival")
# Print first few rows.
print(head(pbc))Quando executamos o código acima, ele produz o seguinte resultado e gráfico -
id time status trt age sex ascites hepato spiders edema bili chol
1 1 400 2 1 58.76523 f 1 1 1 1.0 14.5 261
2 2 4500 0 1 56.44627 f 0 1 1 0.0 1.1 302
3 3 1012 2 1 70.07255 m 0 0 0 0.5 1.4 176
4 4 1925 2 1 54.74059 f 0 1 1 0.5 1.8 244
5 5 1504 1 2 38.10541 f 0 1 1 0.0 3.4 279
6 6 2503 2 2 66.25873 f 0 1 0 0.0 0.8 248
albumin copper alk.phos ast trig platelet protime stage
1 2.60 156 1718.0 137.95 172 190 12.2 4
2 4.14 54 7394.8 113.52 88 221 10.6 3
3 3.48 210 516.0 96.10 55 151 12.0 4
4 2.54 64 6121.8 60.63 92 183 10.3 4
5 3.53 143 671.0 113.15 72 136 10.9 3
6 3.98 50 944.0 93.00 63 NA 11.0 3Com base nos dados acima, estamos considerando o tempo e o status de nossa análise.
Aplicando as funções Surv () e survfit ()
Agora passamos a aplicar o Surv() função para o conjunto de dados acima e crie um gráfico que mostrará a tendência.
# Load the library.
library("survival")
# Create the survival object.
survfit(Surv(pbc$time,pbc$status == 2)~1) # Give the chart file a name. png(file = "survival.png") # Plot the graph. plot(survfit(Surv(pbc$time,pbc$status == 2)~1))
# Save the file.
dev.off()Quando executamos o código acima, ele produz o seguinte resultado e gráfico -
Call: survfit(formula = Surv(pbc$time, pbc$status == 2) ~ 1)
n events median 0.95LCL 0.95UCL
418 161 3395 3090 3853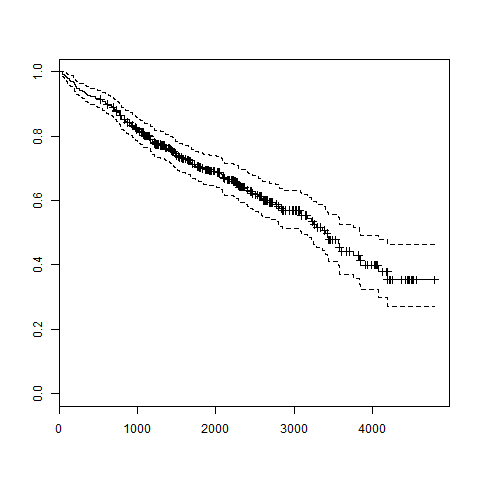
A tendência no gráfico acima nos ajuda a prever a probabilidade de sobrevivência ao final de um determinado número de dias.
Chi-Square testé um método estatístico para determinar se duas variáveis categóricas têm uma correlação significativa entre elas. Ambas as variáveis devem ser da mesma população e devem ser categóricas, como - Sim / Não, Masculino / Feminino, Vermelho / Verde etc.
Por exemplo, podemos construir um conjunto de dados com observações sobre o padrão de compra de sorvete das pessoas e tentar correlacionar o gênero de uma pessoa com o sabor do sorvete de sua preferência. Se uma correlação for encontrada, podemos planejar um estoque apropriado de sabores, sabendo o número de gênero das pessoas que os visitam.
Sintaxe
A função usada para realizar o teste qui-quadrado é chisq.test().
A sintaxe básica para criar um teste qui-quadrado em R é -
chisq.test(data)A seguir está a descrição dos parâmetros usados -
data são os dados em forma de tabela contendo o valor de contagem das variáveis da observação.
Exemplo
Levaremos os dados do Cars93 na biblioteca "MASSA" que representa as vendas de diferentes modelos de automóveis no ano de 1993.
library("MASS")
print(str(Cars93))Quando executamos o código acima, ele produz o seguinte resultado -
'data.frame': 93 obs. of 27 variables:
$ Manufacturer : Factor w/ 32 levels "Acura","Audi",..: 1 1 2 2 3 4 4 4 4 5 ...
$ Model : Factor w/ 93 levels "100","190E","240",..: 49 56 9 1 6 24 54 74 73 35 ... $ Type : Factor w/ 6 levels "Compact","Large",..: 4 3 1 3 3 3 2 2 3 2 ...
$ Min.Price : num 12.9 29.2 25.9 30.8 23.7 14.2 19.9 22.6 26.3 33 ... $ Price : num 15.9 33.9 29.1 37.7 30 15.7 20.8 23.7 26.3 34.7 ...
$ Max.Price : num 18.8 38.7 32.3 44.6 36.2 17.3 21.7 24.9 26.3 36.3 ... $ MPG.city : int 25 18 20 19 22 22 19 16 19 16 ...
$ MPG.highway : int 31 25 26 26 30 31 28 25 27 25 ... $ AirBags : Factor w/ 3 levels "Driver & Passenger",..: 3 1 2 1 2 2 2 2 2 2 ...
$ DriveTrain : Factor w/ 3 levels "4WD","Front",..: 2 2 2 2 3 2 2 3 2 2 ... $ Cylinders : Factor w/ 6 levels "3","4","5","6",..: 2 4 4 4 2 2 4 4 4 5 ...
$ EngineSize : num 1.8 3.2 2.8 2.8 3.5 2.2 3.8 5.7 3.8 4.9 ... $ Horsepower : int 140 200 172 172 208 110 170 180 170 200 ...
$ RPM : int 6300 5500 5500 5500 5700 5200 4800 4000 4800 4100 ... $ Rev.per.mile : int 2890 2335 2280 2535 2545 2565 1570 1320 1690 1510 ...
$ Man.trans.avail : Factor w/ 2 levels "No","Yes": 2 2 2 2 2 1 1 1 1 1 ... $ Fuel.tank.capacity: num 13.2 18 16.9 21.1 21.1 16.4 18 23 18.8 18 ...
$ Passengers : int 5 5 5 6 4 6 6 6 5 6 ... $ Length : int 177 195 180 193 186 189 200 216 198 206 ...
$ Wheelbase : int 102 115 102 106 109 105 111 116 108 114 ... $ Width : int 68 71 67 70 69 69 74 78 73 73 ...
$ Turn.circle : int 37 38 37 37 39 41 42 45 41 43 ... $ Rear.seat.room : num 26.5 30 28 31 27 28 30.5 30.5 26.5 35 ...
$ Luggage.room : int 11 15 14 17 13 16 17 21 14 18 ... $ Weight : int 2705 3560 3375 3405 3640 2880 3470 4105 3495 3620 ...
$ Origin : Factor w/ 2 levels "USA","non-USA": 2 2 2 2 2 1 1 1 1 1 ... $ Make : Factor w/ 93 levels "Acura Integra",..: 1 2 4 3 5 6 7 9 8 10 ...O resultado acima mostra que o conjunto de dados tem muitas variáveis de fator que podem ser consideradas como variáveis categóricas. Para o nosso modelo, consideraremos as variáveis "AirBags" e "Tipo". Pretendemos aqui descobrir qualquer correlação significativa entre os tipos de carro vendidos e o tipo de airbag que possui. Se a correlação for observada, podemos estimar quais tipos de carros podem vender melhor com quais tipos de air bag.
# Load the library.
library("MASS")
# Create a data frame from the main data set.
car.data <- data.frame(Cars93$AirBags, Cars93$Type)
# Create a table with the needed variables.
car.data = table(Cars93$AirBags, Cars93$Type)
print(car.data)
# Perform the Chi-Square test.
print(chisq.test(car.data))Quando executamos o código acima, ele produz o seguinte resultado -
Compact Large Midsize Small Sporty Van
Driver & Passenger 2 4 7 0 3 0
Driver only 9 7 11 5 8 3
None 5 0 4 16 3 6
Pearson's Chi-squared test
data: car.data
X-squared = 33.001, df = 10, p-value = 0.0002723
Warning message:
In chisq.test(car.data) : Chi-squared approximation may be incorrectConclusão
O resultado mostra o valor p inferior a 0,05, o que indica uma correlação de string.