Булева алгебра

Булева алгебра используется для анализа и упрощения цифровых (логических) схем. Он использует только двоичные числа, то есть 0 и 1. Он также называетсяBinary Algebra или logical Algebra. Булева алгебра была изобретенаGeorge Boole в 1854 г.

Правило в булевой алгебре

Ниже приведены важные правила, используемые в булевой алгебре.

• Используемая переменная может иметь только два значения. Двоичный 1 для ВЫСОКОГО и двоичного 0 для НИЗКОГО.

• Дополнение переменной обозначается чертой сверху (-). Таким образом, дополнение переменной B представлено как

  
  . Таким образом, если B = 0, то
  
  = 1 и B = 1, то
  
  = 0.

• Операция ИЛИ переменных обозначается знаком плюс (+) между ними. Например, операция OR для A, B, C представлена ​​как A + B + C.

• Логическое «И» двух или более переменных представлено записью точки между ними, например ABC. Иногда точка может быть опущена, как ABC.

Булевы законы

Есть шесть типов логических законов.

Коммутативный закон

Любая бинарная операция, удовлетворяющая следующему выражению, называется коммутативной операцией.

Закон коммутации гласит, что изменение последовательности переменных не влияет на выходной сигнал логической схемы.

Ассоциативный закон

Этот закон гласит, что порядок, в котором выполняются логические операции, не имеет значения, поскольку их эффект одинаков.

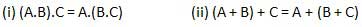
Распределительное право

Распределительный закон устанавливает следующее условие.

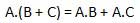
И закон

В этих законах используется операция И. Поэтому их называютAND законы.

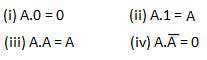
ИЛИ закон

В этих законах используется операция ИЛИ. Поэтому их называютOR законы.

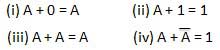
ЗАКОН ИНВЕРСИИ

Этот закон использует операцию НЕ. Закон инверсии гласит, что двойное обращение переменной приводит к самой исходной переменной.

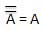
Важные булевы теоремы

Ниже приведены несколько важных булевых теорем.

Булева функция / теоремы	Описание
Булевы функции	Логические функции и выражения, реализация K-Map и NAND Gates
Теоремы Де Моргана	Теорема Де Моргана 1 и теорема 2