Шестнадцатеричная арифметика
Шестнадцатеричная система счисления
Ниже приведены характеристики шестнадцатеричной системы счисления.
Использует 10 цифр и 6 букв, 0,1,2,3,4,5,6,7,8,9, A, B, C, D, E, F.
Буквы обозначают числа, начинающиеся с 10. A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
Также называется системой счисления с основанием 16.
Каждая позиция в шестнадцатеричном числе представляет собой степень 0 основания (16). Пример - 16 0
Последняя позиция в шестнадцатеричном числе представляет собой степень x основания (16). Пример - 16 x, где x представляет последнюю позицию - 1.
пример
Шестнадцатеричное число - 19FDE 16
Расчет десятичного эквивалента -
| Шаг | Шестнадцатеричное число | Десятичное число |
|---|---|---|
| Шаг 1 | 19FDE 16 | ((1 × 16 4 ) + (9 × 16 3 ) + (F × 16 2 ) + (D × 16 1 ) + (E × 16 0 )) 10 |
| Шаг 2 | 19FDE 16 | ((1 × 16 4 ) + (9 × 16 3 ) + (15 × 16 2 ) + (13 × 16 1 ) + (14 × 16 0 )) 10 |
| Шаг 3 | 19FDE 16 | (65536 + 36864 + 3840 + 208 + 14) 10 |
| Шаг 4 | 19FDE 16 | 106462 10 |
Note −19FDE 16 обычно записывается как 19FDE.
Шестнадцатеричное сложение
Следующая таблица шестнадцатеричного сложения очень поможет вам справиться с шестнадцатеричным сложением.
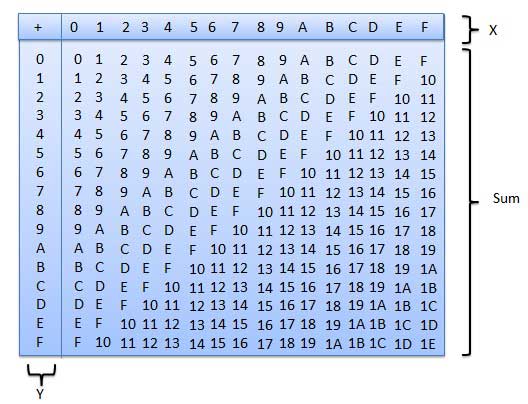
Чтобы использовать эту таблицу, просто следуйте инструкциям, использованным в этом примере - сложите A 16 и 5 16 . Найдите A в столбце X, затем найдите 5 в столбце Y. Точка в области «сумма», где пересекаются эти два столбца, представляет собой сумму двух чисел.
A16 + 516 = F16.Пример - Дополнение
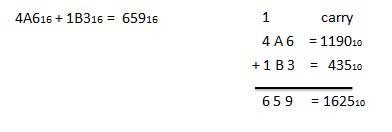
Шестнадцатеричное вычитание
Вычитание шестнадцатеричных чисел осуществляется по тем же правилам, что и вычитание чисел в любой другой системе счисления. Единственная вариация - заимствованное количество. В десятичной системе вы заимствуете группу из 10 10 . В двоичной системе вы заимствуете группу из 2 10 . В шестнадцатеричной системе вы заимствуете группу из 16 10 .
Пример - вычитание
