MATLAB - Арифметические операции
MATLAB позволяет выполнять два разных типа арифметических операций -
- Матричные арифметические операции
- Арифметические операции с массивами
Матричные арифметические операции такие же, как и в линейной алгебре. Операции с массивами выполняются поэлементно, как над одномерным, так и с многомерным массивом.
Матричные операторы и операторы массивов различаются символом точки (.). Однако, поскольку операции сложения и вычитания одинаковы для матриц и массивов, оператор одинаков для обоих случаев.
В следующей таблице дано краткое описание операторов -
| Sr. No. | Оператор и описание |
|---|---|
| 1 | + Дополнение или одинарный плюс. A + B складывает значения, хранящиеся в переменных A и B. A и B должны иметь одинаковый размер, если только один не является скаляром. Скаляр можно добавить к матрице любого размера. |
| 2 | - Вычитание или унарный минус. AB вычитает значение B из A. A и B должны иметь одинаковый размер, если только один не является скаляром. Скаляр можно вычесть из матрицы любого размера. |
| 3 | * Умножение матриц. C = A * B - линейное алгебраическое произведение матриц A и B. Точнее,
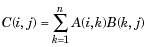
Для нескалярных A и B количество столбцов A должно быть равно количеству строк B. Скаляр может умножать матрицу любого размера. |
| 4 | .* Умножение массива. A. * B - это поэлементное произведение массивов A и B. A и B должны иметь одинаковый размер, если только один из них не является скаляром. |
| 5 | / Косая черта или матричное деление справа. B / A примерно то же самое, что B * inv (A). Точнее, B / A = (A '\ B') '. |
| 6 | ./ Правое деление массива. A./B - матрица с элементами A (i, j) / B (i, j). A и B должны иметь одинаковый размер, если один из них не является скаляром. |
| 7 | \ Обратная косая черта или матричное левое деление. Если A - квадратная матрица, A \ B примерно то же самое, что inv (A) * B, за исключением того, что вычисляется другим способом. Если А является п-по-п матрицы и В представляет собой вектор - столбец с п компонентами, или матрицу с несколькими такими столбцами, то Х = А \ В является решением уравнения AX = B . Предупреждающее сообщение отображается, если A плохо масштабирован или почти единичный. |
| 8 | .\ Левое деление массива. A. \ B - матрица с элементами B (i, j) / A (i, j). A и B должны иметь одинаковый размер, если один из них не является скаляром. |
| 9 | ^ Матрица мощности. X ^ p - это X в степени p, если p - скаляр. Если p - целое число, мощность вычисляется путем повторного возведения в квадрат. Если целое число отрицательное, сначала инвертируется X. Для других значений p в вычислении используются собственные значения и собственные векторы, так что если [V, D] = eig (X), то X ^ p = V * D. ^ p / V. |
| 10 | .^ Мощность массива. A. ^ B - матрица с элементами A (i, j) в степени B (i, j). A и B должны иметь одинаковый размер, если один из них не является скаляром. |
| 11 | ' Матрица транспонирована. A '- это линейное алгебраическое транспонирование A. Для комплексных матриц это комплексно-сопряженное транспонирование. |
| 12 | .' Транспонирование массива. А. ' - это массив, транспонированный к A. Для сложных матриц это не требует сопряжения. |
пример
В следующих примерах показано использование арифметических операторов для скалярных данных. Создайте файл сценария со следующим кодом -
a = 10;
b = 20;
c = a + b
d = a - b
e = a * b
f = a / b
g = a \ b
x = 7;
y = 3;
z = x ^ yКогда вы запускаете файл, он дает следующий результат -
c = 30
d = -10
e = 200
f = 0.50000
g = 2
z = 343Функции для арифметических операций
Помимо вышеупомянутых арифметических операторов, MATLAB предоставляет следующие команды / функции, используемые для аналогичной цели:
| Sr. No. | Описание функции |
|---|---|
| 1 | uplus(a) Унарный плюс; увеличивается на величину a |
| 2 | plus (a,b) Плюс; возвращает a + b |
| 3 | uminus(a) Унарный минус; уменьшается на величину a |
| 4 | minus(a, b) Минус; возвращает a - b |
| 5 | times(a, b) Умножение массива; возвращает a. * b |
| 6 | mtimes(a, b) Умножение матриц; возвращает a * b |
| 7 | rdivide(a, b) Деление правого массива; возвращает a ./ b |
| 8 | ldivide(a, b) Левое деление массива; возвращает a. \ b |
| 9 | mrdivide(A, B) Решите системы линейных уравнений xA = B относительно x |
| 10 | mldivide(A, B) Решите системы линейных уравнений Ax = B относительно x |
| 11 | power(a, b) Мощность массива; возвращает a. ^ b |
| 12 | mpower(a, b) Мощность матрицы; возвращает a ^ b |
| 13 | cumprod(A) Накопительный продукт; возвращает массив того же размера, что и массив A, содержащий совокупный продукт.
|
| 14 | cumprod(A, dim) Возвращает совокупный продукт по размеру dim . |
| 15 | cumsum(A) Накопительная сумма; возвращает массив A, содержащий совокупную сумму.
|
| 16 | cumsum(A, dim) Возвращает совокупную сумму элементов по размеру dim . |
| 17 | diff(X) Различия и приблизительные производные; вычисляет различия между соседними элементами X.
|
| 18 | diff(X,n) Применяет diff рекурсивно n раз, в результате получается n-я разница. |
| 19 | diff(X,n,dim) Это n-я функция разности, вычисляемая по измерению, заданному скалярным dim. Если порядок n равен или превышает длину измерения dim, diff возвращает пустой массив. |
| 20 | prod(A) Произведение элементов массива; возвращает произведение элементов массива A.
Функция prod вычисляет и возвращает B как single, если вход A является одиночным. Для всех остальных числовых и логических типов данных prod вычисляет и возвращает B как double. |
| 21 год | prod(A,dim) Возвращает товары по размеру dim. Например, если A - матрица, prod (A, 2) - вектор-столбец, содержащий произведения каждой строки. |
| 22 | prod(___,datatype) умножается и возвращает массив в классе, заданном типом данных. |
| 23 | sum(A)
|
| 24 | sum(A,dim) Суммирует по размерности A, указанной скалярным dim . |
| 25 | sum(..., 'double') sum(..., dim,'double') Выполните сложение с двойной точностью и верните ответ типа double, даже если A имеет тип данных single или целочисленный тип данных. Это значение по умолчанию для целочисленных типов данных. |
| 26 | sum(..., 'native') sum(..., dim,'native') Выполните добавления в собственном типе данных A и верните ответ того же типа данных. Это значение по умолчанию для одинарных и двойных. |
| 27 | ceil(A) Округлить в сторону положительной бесконечности; округляет элементы A до ближайших целых чисел, больших или равных A. |
| 28 | fix(A) Округлить к нулю |
| 29 | floor(A) Округлить в сторону отрицательной бесконечности; округляет элементы A до ближайших целых чисел, меньших или равных A. |
| 30 | idivide(a, b) idivide(a, b,'fix') Целочисленное деление с возможностью округления; то же самое, что и a./b, за исключением того, что дробные частные округляются в сторону нуля до ближайших целых чисел. |
| 31 год | idivide(a, b, 'round') Дробные частные округляются до ближайшего целого числа. |
| 32 | idivide(A, B, 'floor') Дробные частные округляются в сторону отрицательной бесконечности до ближайших целых чисел. |
| 33 | idivide(A, B, 'ceil') Дробные частные округляются до бесконечности до ближайших целых чисел. |
| 34 | mod (X,Y) Модуль после деления; возвращает X - n. * Y, где n = этаж (X./Y). Если Y не является целым числом, а частное X./Y находится в пределах ошибки округления целого числа, то n является этим целым числом. Входные данные X и Y должны быть реальными массивами одинакового размера или реальными скалярами (при условии, что Y ~ = 0). Обратите внимание -
|
| 35 год | rem (X,Y) Остаток после разделения; возвращает X - n. * Y, где n = fix (X./Y). Если Y не является целым числом, а отношение X./Y находится в пределах ошибки округления целого числа, то n - это целое число. Входные данные X и Y должны быть реальными массивами одинакового размера или реальными скалярами (при условии, что Y ~ = 0). Обратите внимание, что -
|
| 36 | round(X) Округлить до ближайшего целого числа; округляет элементы X до ближайших целых чисел. Положительные элементы с дробной частью 0,5 округляются до ближайшего положительного целого числа. Отрицательные элементы с дробной частью -0,5 округляются до ближайшего отрицательного целого числа. |