MATLAB - Расчет

MATLAB предоставляет различные способы решения задач дифференциального и интегрального исчисления, решения дифференциальных уравнений любой степени и вычисления пределов. Лучше всего то, что вы можете легко построить графики сложных функций и проверить максимумы, минимумы и другие стационарные точки на графике, решив исходную функцию, а также ее производную.

В этой главе будут рассмотрены проблемы исчисления. В этой главе мы обсудим концепции предварительного исчисления, т. Е. Вычисление пределов функций и проверку свойств пределов.

В следующей главе « Дифференциал» мы вычислим производную выражения и найдем локальные максимумы и минимумы на графике. Мы также обсудим решение дифференциальных уравнений.

Наконец, в главе « Интеграция» мы обсудим интегральное исчисление.

Расчет пределов

MATLAB предоставляет limitфункция для расчета пределов. В своей основной формеlimit функция принимает выражение в качестве аргумента и находит предел выражения, когда независимая переменная стремится к нулю.

Например, давайте вычислим предел функции f (x) = (x ³ + 5) / (x ⁴ + 7), когда x стремится к нулю.

syms x
limit((x^3 + 5)/(x^4 + 7))

MATLAB выполнит вышеуказанный оператор и вернет следующий результат -

ans =
   5/7

Функция предела относится к сфере символических вычислений; вам нужно использоватьsymsфункция, чтобы сообщить MATLAB, какие символьные переменные вы используете. Вы также можете вычислить предел функции, поскольку переменная стремится к некоторому числу, отличному от нуля. Чтобы вычислить lim _{x-> a} (f (x)), мы используем команду limit с аргументами. Первое - это выражение, а второе - число, к которому приближается x , здесь это a .

Например, давайте вычислим предел функции f (x) = (x-3) / (x-1), когда x стремится к 1.

limit((x - 3)/(x-1),1)

MATLAB выполнит вышеуказанный оператор и вернет следующий результат -

ans =
   NaN

Возьмем другой пример,

limit(x^2 + 5, 3)

MATLAB выполнит вышеуказанный оператор и вернет следующий результат -

ans =
   14

Расчет пределов с использованием октавы

Ниже приведена Octave-версия приведенного выше примера с использованием symbolic пакет, попробуйте выполнить и сравните результат -

pkg load symbolic
symbols

x = sym("x");
subs((x^3+5)/(x^4+7),x,0)

Octave выполнит вышеуказанный оператор и вернет следующий результат -

ans =
   0.7142857142857142857

Проверка основных свойств пределов.

Алгебраическая предельная теорема дает некоторые основные свойства пределов. Это следующие -

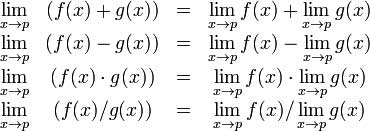
Давайте рассмотрим две функции -

f (x) = (3x + 5) / (x - 3)
г (х) знак равно х ² + 1.

Давайте вычислим пределы функций, когда x стремится к 5, обеих функций и проверим основные свойства пределов, используя эти две функции и MATLAB.

пример

Создайте файл сценария и введите в него следующий код -

syms x
f = (3*x + 5)/(x-3);
g = x^2 + 1;
l1 = limit(f, 4)
l2 = limit (g, 4)
lAdd = limit(f + g, 4)
lSub = limit(f - g, 4)
lMult = limit(f*g, 4)
lDiv = limit (f/g, 4)

Когда вы запускаете файл, он отображает -

l1 =
   17
  
l2 =
   17
  
lAdd =
   34
 
lSub =
   0
  
lMult =
   289
  
lDiv =
   1

Проверка основных свойств пределов с помощью Octave

pkg load symbolic
symbols

x = sym("x");
f = (3*x + 5)/(x-3);
g = x^2 + 1;

l1 = subs(f, x, 4)
l2 = subs (g, x, 4)
lAdd = subs (f+g, x, 4)
lSub = subs (f-g, x, 4)
lMult = subs (f*g, x, 4)
lDiv = subs (f/g, x, 4)

Octave выполнит вышеуказанный оператор и вернет следующий результат -

l1 =
   17.0
l2 =
   17.0
lAdd =
   34.0
lSub =
   0.0
lMult =
   289.0
lDiv =
   1.0

Левый и правый пределы

Когда функция имеет разрыв для некоторого конкретного значения переменной, предел в этой точке не существует. Другими словами, пределы функции f (x) имеют разрыв при x = a, когда значение предела, когда x приближается к x с левой стороны, не равно значению предела, когда x приближается с правой стороны.

Это приводит к концепции ограничения для левой и правой руки. Левый предел определяется как предел как x -> a слева, т. Е. X приближается к a для значений x <a. Правосторонний предел определяется как предел, когда x -> a, справа, т. Е. X приближается к a для значений x> a. Когда левый предел и правый предел не равны, предел не существует.

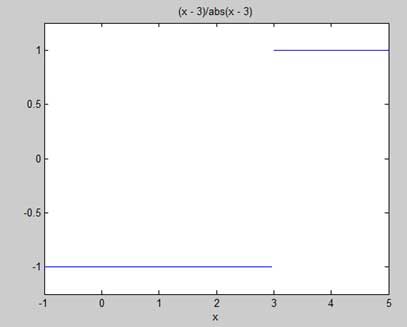
Давайте рассмотрим функцию -

f(x) = (x - 3)/|x - 3|

Покажем, что lim _{x-> 3} f (x) не существует. MATLAB помогает нам установить этот факт двумя способами:

Построив график функции и показывая разрыв.
Вычислив пределы и показывая, что оба они разные.

Пределы для левой и правой руки вычисляются путем передачи символьных строк «left» и «right» команде limit в качестве последнего аргумента.

пример

Создайте файл сценария и введите в него следующий код -

f = (x - 3)/abs(x-3);
ezplot(f,[-1,5])
l = limit(f,x,3,'left')
r = limit(f,x,3,'right')

Когда вы запускаете файл, MATLAB рисует следующий график

После этого отображается следующий вывод -

l =
   -1
  
r =
   1