MATLAB - Интеграция
Интеграция решает два принципиально разных типа проблем.
В первом типе дана производная функции, и мы хотим найти функцию. Таким образом, мы в основном обращаем вспять процесс дифференциации. Этот обратный процесс известен как антидифференциация, или нахождение примитивной функции, или нахождениеindefinite integral.
Второй тип проблем заключается в суммировании очень большого числа очень малых величин и последующем установлении предела, когда размер величин приближается к нулю, в то время как количество членов стремится к бесконечности. Этот процесс приводит к определениюdefinite integral.
Определенные интегралы используются для определения площади, объема, центра тяжести, момента инерции, работы, совершаемой силой, и во многих других приложениях.
Нахождение неопределенного интеграла с помощью MATLAB
По определению, если производная функции f (x) равна f '(x), то мы говорим, что неопределенный интеграл от f' (x) относительно x равен f (x). Например, поскольку производная (по x) x 2 равна 2x, мы можем сказать, что неопределенный интеграл от 2x равен x 2 .
В символах -
f'(x2) = 2x, следовательно,
∫ 2xdx = x2.
Неопределенный интеграл не уникален, потому что производная x 2 + c для любого значения константы c также будет 2x.
Это выражается символами как -
∫ 2xdx = x2 + c.
Где c называется «произвольной константой».
MATLAB предоставляет intкоманда для вычисления интеграла выражения. Чтобы получить выражение для неопределенного интеграла функции, мы пишем -
int(f);Например, из нашего предыдущего примера -
syms x
int(2*x)MATLAB выполняет вышеуказанный оператор и возвращает следующий результат -
ans =
x^2Пример 1
В этом примере давайте найдем интеграл некоторых часто используемых выражений. Создайте файл сценария и введите в него следующий код -
syms x n
int(sym(x^n))
f = 'sin(n*t)'
int(sym(f))
syms a t
int(a*cos(pi*t))
int(a^x)Когда вы запускаете файл, он отображает следующий результат -
ans =
piecewise([n == -1, log(x)], [n ~= -1, x^(n + 1)/(n + 1)])
f =
sin(n*t)
ans =
-cos(n*t)/n
ans =
(a*sin(pi*t))/pi
ans =
a^x/log(a)Пример 2
Создайте файл сценария и введите в него следующий код -
syms x n
int(cos(x))
int(exp(x))
int(log(x))
int(x^-1)
int(x^5*cos(5*x))
pretty(int(x^5*cos(5*x)))
int(x^-5)
int(sec(x)^2)
pretty(int(1 - 10*x + 9 * x^2))
int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2)
pretty(int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2))Обратите внимание, что pretty функция возвращает выражение в более читаемом формате.
Когда вы запускаете файл, он отображает следующий результат -
ans =
sin(x)
ans =
exp(x)
ans =
x*(log(x) - 1)
ans =
log(x)
ans =
(24*cos(5*x))/3125 + (24*x*sin(5*x))/625 - (12*x^2*cos(5*x))/125 + (x^4*cos(5*x))/5 - (4*x^3*sin(5*x))/25 + (x^5*sin(5*x))/5
2 4
24 cos(5 x) 24 x sin(5 x) 12 x cos(5 x) x cos(5 x)
----------- + ------------- - -------------- + ------------
3125 625 125 5
3 5
4 x sin(5 x) x sin(5 x)
------------- + -----------
25 5
ans =
-1/(4*x^4)
ans =
tan(x)
2
x (3 x - 5 x + 1)
ans =
- (7*x^6)/12 - (3*x^5)/5 + (5*x^4)/8 + x^3/2
6 5 4 3
7 x 3 x 5 x x
- ---- - ---- + ---- + --
12 5 8 2Нахождение определенного интеграла с помощью MATLAB
По определению, определенный интеграл - это, по сути, предел суммы. Мы используем определенные интегралы, чтобы найти такие области, как площадь между кривой и осью x и площадь между двумя кривыми. Определенные интегралы могут также использоваться в других ситуациях, когда требуемая величина может быть выражена как предел суммы.
В int Функцию можно использовать для точного интегрирования, перейдя границы, за которые вы хотите вычислить интеграл.
Вычислять
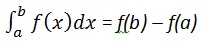
мы пишем,
int(x, a, b)Например, чтобы рассчитать значение,

int(x, 4, 9)MATLAB выполняет вышеуказанный оператор и возвращает следующий результат -
ans =
65/2Ниже приведен октавный эквивалент приведенного выше расчета.
pkg load symbolic
symbols
x = sym("x");
f = x;
c = [1, 0];
integral = polyint(c);
a = polyval(integral, 9) - polyval(integral, 4);
display('Area: '), disp(double(a));Octave выполняет код и возвращает следующий результат -
Area:
32.500Альтернативное решение может быть предоставлено с использованием функции quad (), предоставляемой Octave, следующим образом:
pkg load symbolic
symbols
f = inline("x");
[a, ierror, nfneval] = quad(f, 4, 9);
display('Area: '), disp(double(a));Octave выполняет код и возвращает следующий результат -
Area:
32.500Пример 1
Вычислим площадь, заключенную между осью x, кривой y = x 3 −2x + 5 и ординатами x = 1 и x = 2.
Требуемая площадь определяется как -
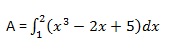
Создайте файл сценария и введите следующий код -
f = x^3 - 2*x +5;
a = int(f, 1, 2)
display('Area: '), disp(double(a));Когда вы запускаете файл, он отображает следующий результат -
a =
23/4
Area:
5.7500Ниже приведен октавный эквивалент приведенного выше расчета.
pkg load symbolic
symbols
x = sym("x");
f = x^3 - 2*x +5;
c = [1, 0, -2, 5];
integral = polyint(c);
a = polyval(integral, 2) - polyval(integral, 1);
display('Area: '), disp(double(a));Octave выполняет код и возвращает следующий результат -
Area:
5.7500Альтернативное решение может быть предоставлено с использованием функции quad (), предоставляемой Octave, следующим образом:
pkg load symbolic
symbols
x = sym("x");
f = inline("x^3 - 2*x +5");
[a, ierror, nfneval] = quad(f, 1, 2);
display('Area: '), disp(double(a));Octave выполняет код и возвращает следующий результат -
Area:
5.7500Пример 2
Найдите площадь под кривой: f (x) = x 2 cos (x) для −4 ≤ x ≤ 9.
Создайте файл сценария и напишите следующий код -
f = x^2*cos(x);
ezplot(f, [-4,9])
a = int(f, -4, 9)
disp('Area: '), disp(double(a));Когда вы запускаете файл, MATLAB строит график -
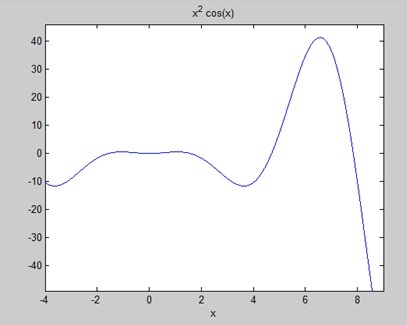
Результат приведен ниже -
a =
8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9)
Area:
0.3326Ниже приведен октавный эквивалент приведенного выше расчета.
pkg load symbolic
symbols
x = sym("x");
f = inline("x^2*cos(x)");
ezplot(f, [-4,9])
print -deps graph.eps
[a, ierror, nfneval] = quad(f, -4, 9);
display('Area: '), disp(double(a));