MATLAB - Полиномы
MATLAB представляет полиномы как векторы-строки, содержащие коэффициенты, упорядоченные по убыванию степеней. Например, уравнение P (x) = x 4 + 7x 3 - 5x + 9 может быть представлено как -
р = [1 7 0 -5 9];
Оценка многочленов
В polyvalФункция используется для вычисления полинома по заданному значению. Например, чтобы оценить наш предыдущий многочленp, при x = 4 введите -
p = [1 7 0 -5 9];
polyval(p,4)MATLAB выполняет вышеуказанные операторы и возвращает следующий результат -
ans = 693MATLAB также предоставляет polyvalmфункция для вычисления матричного полинома. Матричный полином - этоpolynomial с матрицами в качестве переменных.
Например, давайте создадим квадратную матрицу X и вычислим многочлен p, в X -
p = [1 7 0 -5 9];
X = [1 2 -3 4; 2 -5 6 3; 3 1 0 2; 5 -7 3 8];
polyvalm(p, X)MATLAB выполняет вышеуказанные операторы и возвращает следующий результат -
ans =
2307 -1769 -939 4499
2314 -2376 -249 4695
2256 -1892 -549 4310
4570 -4532 -1062 9269Поиск корней многочленов
В rootsфункция вычисляет корни многочлена. Например, чтобы вычислить корни нашего многочлена p, введите -
p = [1 7 0 -5 9];
r = roots(p)MATLAB выполняет вышеуказанные операторы и возвращает следующий результат -
r =
-6.8661 + 0.0000i
-1.4247 + 0.0000i
0.6454 + 0.7095i
0.6454 - 0.7095iФункция polyявляется функцией, обратной корням, и возвращается к полиномиальным коэффициентам. Например -
p2 = poly(r)MATLAB выполняет вышеуказанные операторы и возвращает следующий результат -
p2 =
Columns 1 through 3:
1.00000 + 0.00000i 7.00000 + 0.00000i 0.00000 + 0.00000i
Columns 4 and 5:
-5.00000 - 0.00000i 9.00000 + 0.00000iАппроксимация полиномиальной кривой
В polyfitФункция находит коэффициенты полинома, который соответствует набору данных методом наименьших квадратов. Если x и y - два вектора, содержащие данные x и y, которые нужно подогнать под полином n-й степени, то мы получаем полином, соответствующий данным, записывая -
p = polyfit(x,y,n)пример
Создайте файл сценария и введите следующий код -
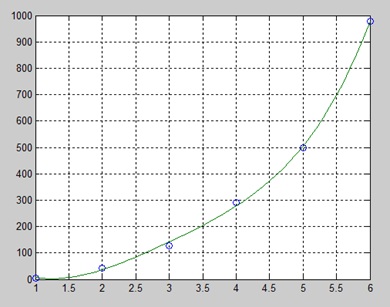
x = [1 2 3 4 5 6]; y = [5.5 43.1 128 290.7 498.4 978.67]; %data
p = polyfit(x,y,4) %get the polynomial
% Compute the values of the polyfit estimate over a finer range,
% and plot the estimate over the real data values for comparison:
x2 = 1:.1:6;
y2 = polyval(p,x2);
plot(x,y,'o',x2,y2)
grid onКогда вы запускаете файл, MATLAB отображает следующий результат -
p =
4.1056 -47.9607 222.2598 -362.7453 191.1250И строит следующий график -