MATLAB - Операторы
Оператор - это символ, который сообщает компилятору о необходимости выполнения определенных математических или логических операций. MATLAB предназначен для работы в первую очередь с целыми матрицами и массивами. Следовательно, операторы в MATLAB работают как со скалярными, так и с нескалярными данными. MATLAB позволяет выполнять следующие типы элементарных операций -
- Арифметические операторы
- Операторы отношения
- Логические операторы
- Побитовые операции
- Установить операции
Арифметические операторы
MATLAB позволяет выполнять два разных типа арифметических операций -
- Матричные арифметические операции
- Арифметические операции с массивами
Матричные арифметические операции такие же, как и в линейной алгебре. Операции с массивами выполняются поэлементно, как над одномерным, так и с многомерным массивом.
Операторы матрицы и операторы массива различаются символом точки (.). Однако, поскольку операции сложения и вычитания одинаковы для матриц и массивов, оператор одинаков для обоих случаев. В следующей таблице дано краткое описание операторов -
Показать примеры
| Sr. No. | Оператор и описание |
|---|---|
| 1 | + Дополнение или одинарный плюс. A + B складывает значения, хранящиеся в переменных A и B. A и B должны иметь одинаковый размер, если только один не является скаляром. Скаляр можно добавить к матрице любого размера. |
| 2 | - Вычитание или унарный минус. AB вычитает значение B из A. A и B должны иметь одинаковый размер, если только один не является скаляром. Скаляр можно вычесть из матрицы любого размера. |
| 3 | * Умножение матриц. C = A * B - линейное алгебраическое произведение матриц A и B. Точнее,
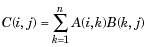
Для нескалярных A и B количество столбцов A должно быть равно количеству строк B. Скаляр может умножать матрицу любого размера. |
| 4 | .* Умножение массива. A. * B - это поэлементное произведение массивов A и B. A и B должны иметь одинаковый размер, если только один из них не является скаляром. |
| 5 | / Косая черта или матричное деление справа. B / A примерно то же самое, что B * inv (A). Точнее, B / A = (A '\ B') '. |
| 6 | ./ Правое деление массива. A./B - матрица с элементами A (i, j) / B (i, j). A и B должны иметь одинаковый размер, если один из них не является скаляром. |
| 7 | \ Обратная косая черта или матричное левое деление. Если A - квадратная матрица, A \ B примерно то же самое, что inv (A) * B, за исключением того, что вычисляется другим способом. Если А является п-по-п матрицы и В представляет собой вектор - столбец с п компонентами, или матрицу с несколькими такими столбцами, то Х = А \ В является решением уравнения AX = B . Предупреждающее сообщение отображается, если A плохо масштабирован или почти единичный. |
| 8 | .\ Левое деление массива. A. \ B - матрица с элементами B (i, j) / A (i, j). A и B должны иметь одинаковый размер, если один из них не является скаляром. |
| 9 | ^ Матрица мощности. X ^ p - это X в степени p, если p - скаляр. Если p - целое число, мощность вычисляется путем повторного возведения в квадрат. Если целое число отрицательное, сначала инвертируется X. Для других значений p в вычислении используются собственные значения и собственные векторы, так что если [V, D] = eig (X), то X ^ p = V * D. ^ p / V. |
| 10 | .^ Мощность массива. A. ^ B - матрица с элементами A (i, j) в степени B (i, j). A и B должны иметь одинаковый размер, если один из них не является скаляром. |
| 11 | ' Матрица транспонирована. A '- это линейное алгебраическое транспонирование A. Для комплексных матриц это комплексно-сопряженное транспонирование. |
| 12 | .' Транспонирование массива. А. ' - это массив, транспонированный к A. Для сложных матриц это не требует сопряжения. |
Операторы отношения
Операторы отношения также могут работать как с скалярными, так и с нескалярными данными. Операторы отношения для массивов выполняют поэлементное сравнение между двумя массивами и возвращают логический массив того же размера с элементами, установленными на логическую 1 (истина), где отношение истинно, и элементами, установленными на логический 0 (ложь), где это не.
В следующей таблице показаны реляционные операторы, доступные в MATLAB -
Показать примеры
| Sr. No. | Оператор и описание |
|---|---|
| 1 | < Меньше, чем |
| 2 | <= Меньше или равно |
| 3 | > Лучше чем |
| 4 | >= Больше или равно |
| 5 | == Равно |
| 6 | ~= Не равно |
Логические операторы
MATLAB предлагает два типа логических операторов и функций -
Поэлементно - эти операторы работают с соответствующими элементами логических массивов.
Короткое замыкание - эти операторы работают со скалярными и логическими выражениями.
Поэлементные логические операторы работают с логическими массивами поэлементно. Символы &, | и ~ являются операторами логического массива И, ИЛИ и НЕ.
Логические операторы короткого замыкания позволяют замыкать логические операции. Символы && и || - логические операторы короткого замыкания И и ИЛИ.
Показать примеры
Побитовые операции
Побитовые операторы работают с битами и выполняют побитовые операции. Таблицы истинности для &, | и ^ следующие:
| п | q | p & q | p | q | p ^ q |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 |
Допустим, если A = 60; и B = 13; Теперь в двоичном формате они будут такими:
А = 0011 1100
В = 0000 1101
-----------------
A&B = 0000 1100
А | В = 0011 1101
A ^ B = 0011 0001
~ А = 1100 0011
MATLAB предоставляет различные функции для побитовых операций, таких как операции «побитовое и», «побитовое или» и «побитовое не», операция сдвига и т. Д.
В следующей таблице показаны часто используемые побитовые операции -
Показать примеры
| Функция | Цель |
|---|---|
| битанд (а, б) | Побитовое И целых чисел a и b |
| bitcmp (а) | Двоичное дополнение а |
| bitget (a, pos) | Получить бит в указанной позиции pos в целочисленном массиве a |
| битор (а, б) | Побитовое ИЛИ целых чисел a и b |
| bitset (a, pos) | Набор бит в определенном месте поз из а |
| битовый сдвиг (а, к) | Возвращает сдвинуто влево на K битов, что эквивалентно умножению на 2 к . Отрицательные значения k соответствуют сдвигу битов вправо или делению на 2 | k | и округление до ближайшего целого числа в сторону отрицательной бесконечности. Любые биты переполнения усекаются. |
| bitxor (а, б) | Побитовое исключающее ИЛИ целых чисел a и b |
| swapbytes | Поменять местами порядок байтов |
Установить операции
MATLAB предоставляет различные функции для операций с множеством, такие как объединение, пересечение и проверка принадлежности к множеству и т. Д.
В следующей таблице показаны некоторые часто используемые операции с наборами -
Показать примеры
| Sr. No. | Описание функции |
|---|---|
| 1 | intersect(A,B) Установить пересечение двух массивов; возвращает значения, общие для A и B. Возвращаемые значения отсортированы. |
| 2 | intersect(A,B,'rows') Обрабатывает каждую строку A и каждую строку B как отдельные объекты и возвращает строки, общие для A и B. Строки возвращенной матрицы отсортированы. |
| 3 | ismember(A,B) Возвращает массив того же размера, что и A, содержащий 1 (истина), где элементы A находятся в B. В другом месте он возвращает 0 (ложь). |
| 4 | ismember(A,B,'rows') Обрабатывает каждую строку A и каждую строку B как отдельные объекты и возвращает вектор, содержащий 1 (истина), где строки матрицы A также являются строками B. В другом месте он возвращает 0 (ложь). |
| 5 | issorted(A) Возвращает логическую 1 (истина), если элементы A находятся в отсортированном порядке, и логический 0 (ложь) в противном случае. Вход A может быть вектором или массивом ячеек N на 1 или 1 на N строк.A is considered to be sorted if A и выход sort (A) равны. |
| 6 | issorted(A, 'rows') Возвращает логическую 1 (истина), если строки двумерной матрицы A находятся в отсортированном порядке, и логический 0 (ложь) в противном случае. Matrix A is considered to be sorted if A и результат сортировки (A) равен. |
| 7 | setdiff(A,B) Устанавливает разницу двух массивов; возвращает значения в A, которых нет в B. Значения в возвращаемом массиве отсортированы. |
| 8 | setdiff(A,B,'rows') Обрабатывает каждую строку A и каждую строку B как отдельные объекты и возвращает строки из A, которых нет в B. Строки возвращенной матрицы расположены в отсортированном порядке. Параметр "rows" не поддерживает массивы ячеек. |
| 9 | setxor Устанавливает исключающее ИЛИ двух массивов |
| 10 | union Устанавливает объединение двух массивов |
| 11 | unique Уникальные значения в массиве |