การออกแบบ VLSI - ทรานซิสเตอร์ MOS
เทคโนโลยี MOSFET เสริม (CMOS) ใช้กันอย่างแพร่หลายในปัจจุบันเพื่อสร้างวงจรในการใช้งานที่หลากหลายและหลากหลาย คอมพิวเตอร์ซีพียูและโทรศัพท์มือถือในปัจจุบันใช้ประโยชน์จาก CMOS เนื่องจากข้อดีหลายประการ CMOS ให้การกระจายพลังงานต่ำความเร็วค่อนข้างสูงขอบสัญญาณรบกวนสูงในทั้งสองสถานะและจะทำงานกับแรงดันไฟฟ้าต้นทางและอินพุตที่หลากหลาย (หากแรงดันไฟฟ้าของแหล่งจ่ายคงที่)
สำหรับกระบวนการที่เราจะพูดถึงประเภทของทรานซิสเตอร์ที่มีคือ Metal-Oxide-Semiconductor Field Effect Transistor (MOSFET) ทรานซิสเตอร์เหล่านี้เกิดขึ้นas a ‘sandwich’ประกอบด้วยชั้นเซมิคอนดักเตอร์โดยปกติจะเป็นชิ้นหรือแผ่นเวเฟอร์จากผลึกซิลิกอนเดี่ยว ชั้นของซิลิกอนไดออกไซด์ (ออกไซด์) และชั้นของโลหะ
โครงสร้างของ MOSFET
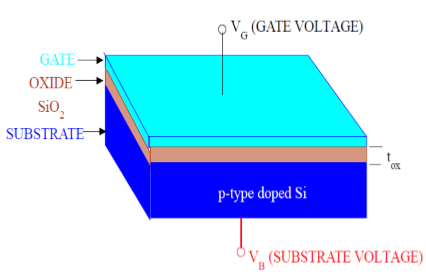
ดังแสดงในรูปโครงสร้าง MOS ประกอบด้วยสามชั้น -
The Metal Gate Electrode
The Insulating Oxide Layer (SiO2)
P – type Semiconductor (Substrate)
โครงสร้าง MOS เป็นตัวเก็บประจุโดยมีประตูและพื้นผิวเป็นแผ่นสองแผ่นและชั้นออกไซด์เป็นวัสดุอิเล็กทริก ความหนาของวัสดุอิเล็กทริก (SiO 2 ) มักอยู่ระหว่าง 10 นาโนเมตรถึง 50 นาโนเมตร ความเข้มข้นและการกระจายตัวของพาหะภายในวัสดุพิมพ์สามารถจัดการได้โดยแรงดันภายนอกที่ใช้กับประตูและขั้วของวัสดุพิมพ์ ตอนนี้เพื่อทำความเข้าใจโครงสร้างของ MOS ก่อนอื่นให้พิจารณาคุณสมบัติทางไฟฟ้าพื้นฐานของสารตั้งต้นเซมิคอนดักเตอร์ชนิด P
ความเข้มข้นของตัวพาในวัสดุเซมิคอนดักเตอร์เป็นไปตาม Mass Action Law. Mass Action Law กำหนดโดย -
$$ np = n_ {i} ^ {2} $$
ที่ไหน
n คือความเข้มข้นของอิเล็กตรอนแบบพาหะ
p คือผู้ให้บริการความเข้มข้นของรู
ni เป็นความเข้มข้นของผู้ให้บริการภายในของซิลิคอน
ตอนนี้ถือว่าพื้นผิวที่มีการเจืออย่างเท่าเทียมกันกับใบเสร็จ (โบรอน) ความเข้มข้น N ดังนั้นความเข้มข้นของอิเล็กตรอนและโฮลในสารตั้งต้นชนิด p คือ
$$ n_ {po} = \ frac {n_ {i} ^ {2}} {N_ {A}} $$
$$ p_ {po} = N_ {A} $$
ที่นี่ความเข้มข้นของยาสลบ NAคือ (10 15ถึง 10 16ซม. −3 ) มากกว่าความเข้มข้นภายใน ni ตอนนี้เพื่อทำความเข้าใจโครงสร้าง MOS ให้พิจารณาแผนภาพระดับพลังงานของพื้นผิวซิลิคอนชนิด p
ดังแสดงในรูปช่องว่างของวงดนตรีระหว่างแถบการนำไฟฟ้าและแถบคาดเอวคือ 1.1eV ที่นี่ Fermi potential Φ Fคือความแตกต่างระหว่างระดับภายใน Fermi (E i ) และระดับ Fermi (E FP )
โดยที่ Fermi ระดับ E Fขึ้นอยู่กับความเข้มข้นของยาสลบ Fermi potential Φ Fคือความแตกต่างระหว่างระดับภายใน Fermi (E i ) และระดับ Fermi (E FP )
ในทางคณิตศาสตร์
$$ \ Phi_ {Fp} = \ frac {E_ {F} -E_ {i}} {q} $$
ความต่างศักย์ระหว่างแถบการนำไฟฟ้าและพื้นที่ว่างเรียกว่าความสัมพันธ์ของอิเล็กตรอนและแสดงด้วย qx
ดังนั้นพลังงานที่จำเป็นสำหรับอิเล็กตรอนในการเคลื่อนที่จากระดับเฟอร์มิไปยังพื้นที่ว่างเรียกว่าฟังก์ชันการทำงาน (qΦ S ) และได้รับจาก
$$ q \ Phi _ {s} = (E_ {c} -E_ {F}) + qx $$
รูปต่อไปนี้แสดงแผนภาพแถบพลังงานของส่วนประกอบที่ประกอบเป็น MOS
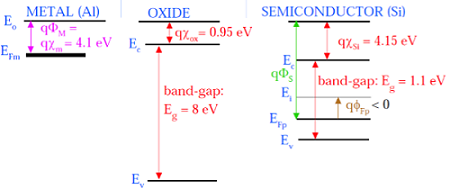
ดังแสดงในรูปด้านบนฉนวนชั้นSiO 2มีช่องว่างแถบพลังงานขนาดใหญ่ที่ 8eV และฟังก์ชันการทำงานเท่ากับ 0.95 eV ประตูโลหะมีฟังก์ชันการทำงาน 4.1eV ที่นี่ฟังก์ชั่นการทำงานแตกต่างกันดังนั้นมันจะสร้างแรงดันตกคร่อมระบบ MOS รูปด้านล่างแสดงแผนภาพแถบพลังงานรวมของระบบ MOS
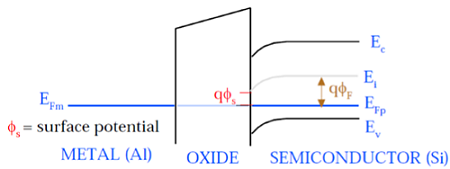
ดังแสดงในรูปนี้ระดับศักย์ไฟฟ้าของประตูโลหะและเซมิคอนดักเตอร์ (Si) มีศักยภาพเท่ากัน ศักยภาพของเฟอร์มีที่พื้นผิวเรียกว่าศักย์พื้นผิวΦ Sและมีขนาดเล็กกว่าศักยภาพเฟอร์มิ i Fในขนาด
การทำงานของ MOSFET
MOSFET ประกอบด้วยตัวเก็บประจุ MOS ที่มีทางแยก pn สองตัววางปิดกับพื้นที่ช่องสัญญาณและพื้นที่นี้ถูกควบคุมโดยแรงดันประตู ในการทำให้ทางแยก pn ทั้งสองมีความเอนเอียงแบบย้อนกลับศักยภาพของสารตั้งต้นจะต่ำกว่าศักยภาพของขั้วต่ออีกสามขั้ว
หากแรงดันเกตเพิ่มขึ้นเกินขีด จำกัด แรงดันไฟฟ้า (V GS > V TO ) ชั้นผกผันจะถูกสร้างขึ้นบนพื้นผิวและช่องประเภท n จะเกิดขึ้นระหว่างแหล่งจ่ายและท่อระบายน้ำ นี้ n - ช่องประเภทจะดำเนินการระบายน้ำในปัจจุบันให้เป็นไปตาม V DSคุ้มค่า
สำหรับค่า V DS ที่แตกต่างกันMOSFET สามารถใช้งานได้ในภูมิภาคต่างๆตามที่อธิบายไว้ด้านล่าง
ภูมิภาคเชิงเส้น
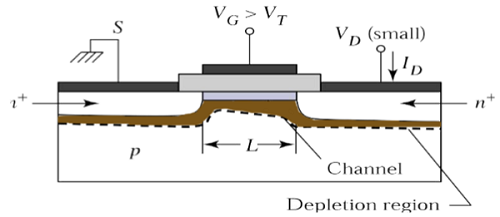
ที่ V DS = 0 สมดุลทางความร้อนมีอยู่ในพื้นที่ช่องกลับด้านและระบายกระแส I D = 0 ตอนนี้ถ้าแรงดันท่อระบายน้ำขนาดเล็กใช้ V DS > 0 กระแสระบายที่เป็นสัดส่วนกับ V DSจะเริ่มไหลจากแหล่งที่มาไปยัง ระบายผ่านช่อง
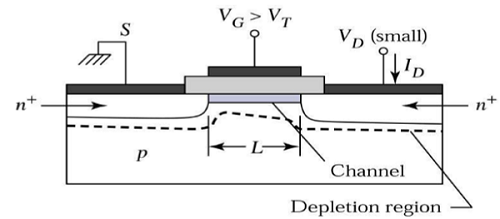
ช่องสัญญาณให้เส้นทางต่อเนื่องสำหรับการไหลของกระแสจากแหล่งที่มาไปยังท่อระบายน้ำ โหมดการทำงานนี้เรียกว่าlinear region. มุมมองภาพตัดขวางของ MOSFET แบบ n-channel ซึ่งทำงานในพื้นที่เชิงเส้นแสดงในรูปด้านล่าง
ที่ Edge of Saturation Region
ตอนนี้ถ้า V DSเพิ่มขึ้นประจุในช่องสัญญาณและความลึกของช่องจะลดลงเมื่อสิ้นสุดท่อระบายน้ำ สำหรับ V DS = V DSATประจุในช่องสัญญาณจะลดลงเป็นศูนย์ซึ่งเรียกว่าpinch – off point. มุมมองภาพตัดขวางของ N-channel MOSFET ที่ทำงานที่ขอบของขอบเขตความอิ่มตัวจะแสดงในรูปด้านล่าง
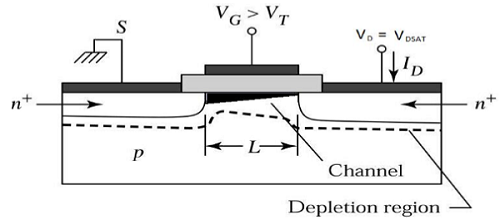
ภาคความอิ่มตัว
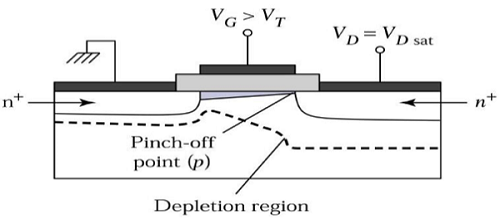
สำหรับ V DS > V DSATพื้นผิวที่หมดอยู่ใกล้จะระบายออกและโดยการเพิ่มแรงดันไฟฟ้าของท่อระบายน้ำบริเวณที่หมดลงนี้จะขยายไปยังแหล่งกำเนิด
โหมดการทำงานนี้เรียกว่า Saturation region. อิเล็กตรอนที่มาจากแหล่งกำเนิดไปยังปลายช่องป้อนในบริเวณท่อระบายน้ำ - พื้นที่พร่องและถูกเร่งไปยังท่อระบายน้ำในสนามไฟฟ้าสูง
MOSFET Current - ลักษณะแรงดันไฟฟ้า
เพื่อทำความเข้าใจลักษณะกระแส - แรงดันไฟฟ้าของ MOSFET การประมาณสำหรับช่องสัญญาณเสร็จสิ้น หากไม่มีการประมาณนี้การวิเคราะห์สามมิติของระบบ MOS จะซับซ้อน Gradual Channel Approximation (GCA) สำหรับลักษณะแรงดันไฟฟ้าในปัจจุบันจะช่วยลดปัญหาในการวิเคราะห์
การประมาณช่องแบบค่อยเป็นค่อยไป (GCA)
พิจารณามุมมองตัดขวางของ n channel MOSFET ที่ทำงานในโหมดเชิงเส้น ที่นี่แหล่งที่มาและวัสดุพิมพ์เชื่อมต่อกับพื้นดิน V S = V B = 0 ประตู - เพื่อ - แหล่งที่มา (V GS ) และท่อระบายน้ำ - เพื่อ - แรงดันไฟฟ้าที่แหล่งที่มา (V DS ) แรงดันไฟฟ้าที่เป็นพารามิเตอร์ภายนอกที่ควบคุมการระบายน้ำในปัจจุบันผมD
แรงดันไฟฟ้า V GSถูกตั้งค่าเป็นแรงดันไฟฟ้าที่มากกว่าแรงดันไฟฟ้าเกณฑ์ V TOเพื่อสร้างช่องระหว่างแหล่งจ่ายและท่อระบายน้ำ ดังแสดงในรูปทิศทาง x ตั้งฉากกับพื้นผิวและทิศทาง y ขนานกับพื้นผิว
ที่นี่ y = 0 ที่ปลายต้นทางดังแสดงในรูป แรงดันไฟฟ้าของช่องเกี่ยวกับแหล่งที่มาจะแสดงโดยVC(Y). สมมติว่าแรงดันไฟฟ้าเกณฑ์ VTO คงที่ตามพื้นที่ช่องระหว่าง y = 0 ถึง y = L เงื่อนไขขอบเขตสำหรับแรงดันช่อง V Cคือ -
$$ V_ {c} \ left (y = 0 \ right) = V_ {s} = 0 \ และ \, V_ {c} \ left (y = L \ right) = V_ {DS} $$
เรายังสามารถสันนิษฐานได้ว่า
$$ V_ {GS} \ geq V_ {TO} $$ และ
$$ V_ {GD} = V_ {GS} -V_ {DS} \ geq V_ {TO} $$
ให้ Q1 (y) เป็นประจุอิเล็กตรอนเคลื่อนที่ทั้งหมดในชั้นผกผันของพื้นผิว ประจุอิเล็กตรอนนี้สามารถแสดงเป็น -
$$ Q1 (y) = - C_ {ox}. [V_ {GS} -V_ {C (Y)} - V_ {TO}] $$
รูปด้านล่างแสดงรูปทรงเรขาคณิตเชิงพื้นที่ของชั้นผกผันพื้นผิวและระบุขนาดของมัน ชั้นผกผันจะเรียวลงเมื่อเราย้ายจากท่อระบายน้ำไปยังแหล่งที่มา ตอนนี้ถ้าเราพิจารณาสีย้อมพื้นที่เล็ก ๆ ของความยาวช่อง L แล้วความต้านทานที่เพิ่มขึ้น dR ที่เสนอโดยภูมิภาคนี้สามารถแสดงเป็น
$$ dR = - \ frac {dy} {w. \ mu _ {n} .Q1 (y)} $$
ที่นี่เครื่องหมายลบเกิดจากขั้วลบของประจุชั้นผกผัน Q1 และμ nคือความคล่องตัวของพื้นผิวซึ่งคงที่ ตอนนี้แทนที่ค่าของ Q1 (y) ในสมการ dR -
$$ dR = - \ frac {dy} {w. \ mu _ {n}. \ left \ {-C_ {ox} \ left [V_ {GS} -V_ {C \ left (Y \ right)} \ right ] -V_ {TO} \ right \}} $$
$$ dR = \ frac {dy} {w. \ mu _ {n} .C_ {ox} \ left [V_ {GS} -V_ {C \ left (Y \ right)} \ right] -V_ {TO} } $$
ตอนนี้แรงดันตกในพื้นที่ dy ขนาดเล็กสามารถกำหนดได้
$$ dV_ {c} = I_ {D} .dR $$
ใส่ค่าของ dR ในสมการด้านบน
$$ dV_ {C} = I_ {D}. \ frac {dy} {w. \ mu_ {n} .C_ {ox} \ left [V_ {GS} -V_ {C (Y)} \ right] -V_ {TO}} $$
$$ w. \ mu _ {n} .C_ {ox} \ left [V_ {GS} -V_ {C (Y)} - V_ {TO} \ right] .dV_ {C} = I_ {D} .dy $$
เพื่อให้ได้ ID ปัจจุบันของท่อระบายน้ำในพื้นที่ช่องสัญญาณทั้งหมดสมการข้างต้นสามารถรวมเข้ากับช่องจาก y = 0 ถึง y = L และแรงดันไฟฟ้า V C (y) = 0 ถึง V C (y) = V DS ,
$$ C_ {ox} .w. \ mu _ {n}. \ int_ {V_ {c} = 0} ^ {V_ {DS}} \ left [V_ {GS} -V_ {C \ left (Y \ right )} - V_ {TO} \ right] .dV_ {C} = \ int_ {Y = 0} ^ {L} I_ {D} .dy $$
$$ \ frac {C_ {ox} .w. \ mu _ {n}} {2} \ left (2 \ left [V_ {GS} -V_ {TO} \ right] V_ {DS} -V_ {DS} ^ {2} \ right) = I_ {D} \ left [L-0 \ right] $$
$$ I_ {D} = \ frac {C_ {ox}. \ mu _ {n}} {2}. \ frac {w} {L} \ left (2 \ left [V_ {GS} -V_ {TO} \ right] V_ {DS} -V_ {DS} ^ {2} \ right) $$
สำหรับภูมิภาคเชิงเส้น V DS <V GS - V TO สำหรับพื้นที่อิ่มตัวค่าของ V DSจะมากกว่า (V GS - V TO ) ดังนั้นสำหรับพื้นที่อิ่มตัว V DS = (V GS - V TO )
$$ I_ {D} = C_ {ox}. \ mu _ {n}. \ frac {w} {2} \ left (\ frac {\ left [2V_ {DS} \ right] V_ {DS} -V_ { DS} ^ {2}} {L} \ right) $$
$$ I_ {D} = C_ {ox}. \ mu _ {n}. \ frac {w} {2} \ left (\ frac {2V_ {DS} ^ {2} -V_ {DS} ^ {2} } {L} \ right) $$
$$ I_ {D} = C_ {ox}. \ mu _ {n}. \ frac {w} {2} \ left (\ frac {V_ {DS} ^ {2}} {L} \ right) $$
$$ I_ {D} = C_ {ox}. \ mu _ {n}. \ frac {w} {2} \ left (\ frac {\ left [V_ {GS} -V_ {TO} \ right] ^ { 2}} {L} \ right) $$