2D Dönüşüm
Dönüşüm, bazı grafikleri kurallar uygulayarak başka bir şeye dönüştürmek anlamına gelir. Çevirme, büyütme veya küçültme, döndürme, yamultma, vb. Gibi çeşitli dönüştürme türlerine sahip olabiliriz. Bir 2D düzlemde bir dönüşüm gerçekleştiğinde, buna 2D dönüştürme denir.
Dönüşümler, ekrandaki grafikleri yeniden konumlandırmak ve boyutlarını veya yönlerini değiştirmek için bilgisayar grafiklerinde önemli bir rol oynar.
Homojen Koordinatlar
Çevirme ve ardından döndürme ve ölçekleme gibi bir dönüşüm dizisi gerçekleştirmek için, sıralı bir süreci izlememiz gerekir -
- Koordinatları çevirin,
- Çevrilen koordinatları döndürün ve ardından
- Bileşik dönüştürmeyi tamamlamak için döndürülen koordinatları ölçekleyin.
Bu süreci kısaltmak için 2 × 2 dönüşüm matrisi yerine 3 × 3 dönüşüm matrisi kullanmalıyız. 2 × 2 matrisi 3 × 3 matrise dönüştürmek için fazladan bir yapay koordinat W eklemeliyiz.
Bu şekilde noktayı 2 sayı yerine 3 sayı ile temsil edebiliriz ki buna Homogenous Coordinatesistemi. Bu sistemde tüm dönüşüm denklemlerini matris çarpımında temsil edebiliriz. Herhangi bir Kartezyen noktası P (X, Y), P '(X h , Y h , h) ile homojen koordinatlara dönüştürülebilir .
Tercüme
Çeviri, bir nesneyi ekranda farklı bir konuma taşır. Yeni koordinatı (X ', Y') elde etmek için orijinal koordinata (X, Y) çeviri koordinatını (t x , t y ) ekleyerek 2B'de bir noktayı çevirebilirsiniz .
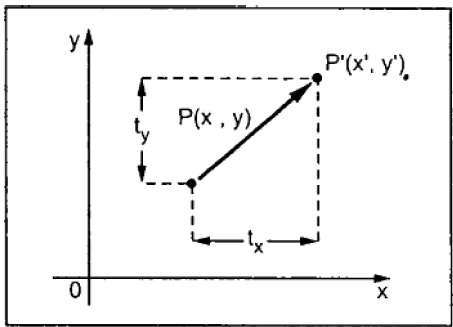
Yukarıdaki şekilden şunu yazabilirsiniz -
X’ = X + tx
Y’ = Y + ty
Çift (t x , t y ), çeviri vektörü veya kaydırma vektörü olarak adlandırılır. Yukarıdaki denklemler, sütun vektörleri kullanılarak da gösterilebilir.
$ P = \ frac {[X]} {[Y]} $ p '= $ \ frac {[X']} {[Y ']} $ T = $ \ frac {[t_ {x}]} {[ t_ {y}]} $
Bunu şu şekilde yazabiliriz -
P’ = P + T
Rotasyon
Dönüşte, nesneyi başlangıç noktasından belirli bir θ (teta) açısıyla döndürürüz. Aşağıdaki şekilden, P (X, Y) noktasının, orijinden r mesafesi ile yatay X koordinatından φ açısında bulunduğunu görebiliriz.
Θ açısında döndürmek istediğinizi varsayalım. Yeni bir konuma döndürdükten sonra, yeni bir P '(X', Y ') noktası alacaksınız.

Standart trigonometrik kullanılarak P (X, Y) noktasının orijinal koordinatı şu şekilde gösterilebilir:
$ X = r \, cos \, \ phi ...... (1) $
$ Y = r \, sin \, \ phi ...... (2) $
Aynı şekilde P '(X', Y ') noktasını -
$ {x} '= r \: cos \: \ left (\ phi \: + \: \ theta \ right) = r \: cos \: \ phi \: cos \: \ theta \: - \: r \ : sin \: \ phi \: sin \: \ theta ....... (3) $
$ {y} '= r \: sin \: \ left (\ phi \: + \: \ theta \ right) = r \: cos \: \ phi \: sin \: \ theta \: + \: r \ : sin \: \ phi \: cos \: \ theta ....... (4) $
Sırasıyla (3) ve (4) 'te (1) ve (2) denklemini değiştirerek
$ {x} '= x \: cos \: \ theta - \: y \: sin \: \ theta $
$ {y} '= x \: sin \: \ theta + \: y \: cos \: \ theta $
Yukarıdaki denklemi matris formunda temsil eden,
$$ [X 'Y'] = [XY] \ begin {bmatrix} cos \ theta & sin \ theta \\ −sin \ theta & cos \ theta \ end {bmatrix} OR $$
P '= P. R
R, rotasyon matrisidir
$$ R = \ begin {bmatrix} cos \ theta & sin \ theta \\ −sin \ theta & cos \ theta \ end {bmatrix} $$
Dönüş açısı pozitif ve negatif olabilir.
Pozitif dönüş açısı için yukarıdaki rotasyon matrisini kullanabiliriz. Ancak, negatif açı dönüşü için, matris aşağıda gösterildiği gibi değişecektir -
$$ R = \ begin {bmatrix} cos (- \ theta) & sin (- \ theta) \\ -sin (- \ theta) & cos (- \ theta) \ end {bmatrix} $$
$$ = \ begin {bmatrix} cos \ theta & −sin \ theta \\ sin \ theta & cos \ theta \ end {bmatrix} \ left (\ çünkü cos (- \ theta) = cos \ theta \; ve \; sin (- \ theta) = −sin \ theta \ right) $$
Ölçeklendirme
Bir nesnenin boyutunu değiştirmek için ölçeklendirme dönüşümü kullanılır. Ölçekleme sürecinde, nesnenin boyutlarını genişletir veya sıkıştırırsınız. Ölçekleme, istenen sonucu elde etmek için nesnenin orijinal koordinatlarını ölçekleme faktörüyle çarparak elde edilebilir.
Orijinal koordinatların (X, Y), ölçekleme faktörlerinin (S X , S Y ) ve üretilen koordinatların (X ', Y') olduğunu varsayalım . Bu, aşağıda gösterildiği gibi matematiksel olarak temsil edilebilir -
X' = X . SX and Y' = Y . SY
Ölçekleme faktörü S X , S Y , nesneyi sırasıyla X ve Y yönünde ölçeklendirir. Yukarıdaki denklemler aşağıdaki gibi matris formunda da gösterilebilir -
$$ \ binom {X '} {Y'} = \ binom {X} {Y} \ begin {bmatrix} S_ {x} & 0 \\ 0 & S_ {y} \ end {bmatrix} $$
VEYA
P’ = P . S
S ölçekleme matrisidir. Ölçekleme işlemi aşağıdaki şekilde gösterilmektedir.
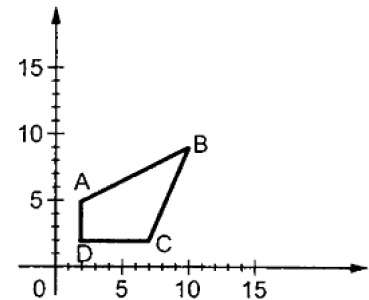
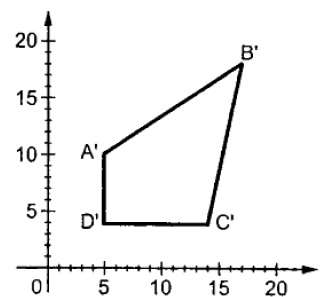
S ölçekleme faktörüne 1'den küçük değerler verirsek, nesnenin boyutunu küçültebiliriz. 1'den büyük değerler sağlarsak, nesnenin boyutunu artırabiliriz.
Yansıma
Yansıma, orijinal nesnenin ayna görüntüsüdür. Yani 180 ° 'lik bir rotasyon işlemi olduğunu söyleyebiliriz. Yansıma dönüşümünde, nesnenin boyutu değişmez.
Aşağıdaki şekiller, sırasıyla X ve Y eksenlerine göre ve orijine ilişkin yansımaları göstermektedir.
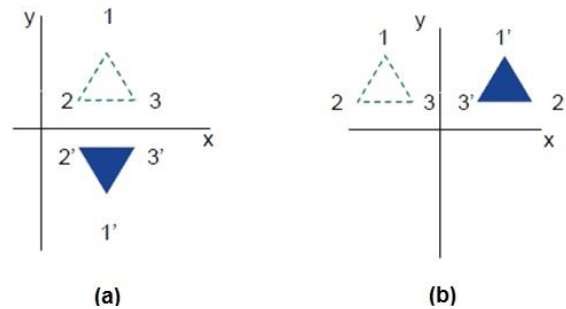
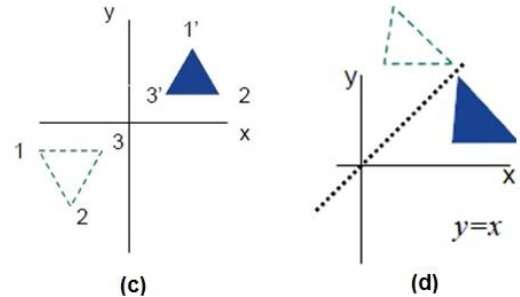
Kesme
Bir nesnenin şeklini eğimli hale getiren bir dönüşüme kesme dönüşümü denir. İki kayma dönüşümü vardırX-Shear ve Y-Shear. Biri X koordinat değerlerini, diğeri Y koordinat değerlerini kaydırır. Ancak; her iki durumda da yalnızca bir koordinat koordinatlarını değiştirir ve diğeri değerlerini korur. Kesme ayrıca şu şekilde adlandırılır:Skewing.
X-Shear
X-Shear, Y koordinatını korur ve X koordinatlarında değişiklikler yapılır, bu da dikey çizgilerin aşağıdaki şekilde gösterildiği gibi sağa veya sola eğilmesine neden olur.
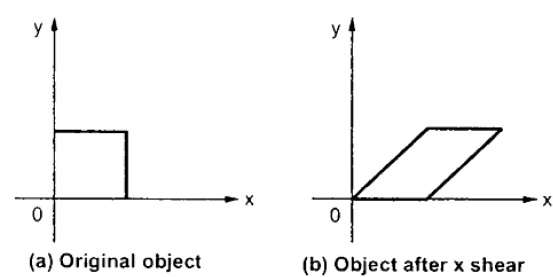
X-Shear için dönüşüm matrisi şu şekilde temsil edilebilir:
$$ X_ {sh} = \ başla {bmatrix} 1 & shx & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} $$
Y '= Y + Sh y . X
X '= X
Y-Kesme
Y Kayması, X koordinatlarını korur ve Y koordinatlarını değiştirerek yatay çizgilerin aşağıdaki şekilde gösterildiği gibi yukarı veya aşağı eğimli çizgilere dönüşmesine neden olur.
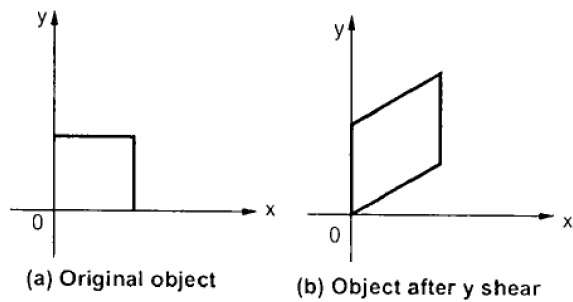
Y-Shear aşağıdaki gibi matriste gösterilebilir:
$$ Y_ {sh} \ başla {bmatrix} 1 & 0 & 0 \\ utangaç & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} $$
X '= X + Sh x . Y
Y '= Y
Kompozit Dönüşüm
T1 düzleminin bir dönüşümünü ikinci bir düzlem dönüşümü T2 takip ediyorsa, o zaman sonucun kendisi, bu sırayla alınan T1 ve T2'nin bileşimi olan tek bir dönüşüm T ile temsil edilebilir. Bu, T = T1 ∙ T2 şeklinde yazılır.
Birleşik dönüşüm, birleşik bir dönüşüm matrisi elde etmek için dönüşüm matrislerinin birleştirilmesiyle elde edilebilir.
Birleşik bir matris -
[T][X] = [X] [T1] [T2] [T3] [T4] …. [Tn]
[Ti] şunun herhangi bir kombinasyonu
- Translation
- Scaling
- Shearing
- Rotation
- Reflection
Dönüşüm sırasındaki değişiklik, genel matris çarpımının kümülatif olmadığı, yani [A] olduğu için farklı sonuçlara yol açacaktır. [B] ≠ [B]. [A] ve çarpma sırası. Dönüşümleri oluşturmanın temel amacı, bir dizi dönüşümü arka arkaya uygulamak yerine, bir noktaya tek bir bileşik dönüşüm uygulayarak verimlilik elde etmektir.
Örneğin, bir nesneyi gelişigüzel bir nokta (X p , Y p ) etrafında döndürmek için , üç adım gerçekleştirmeliyiz -
- Noktayı (X p , Y p ) orijine çevirin.
- Başlangıç noktası etrafında döndürün.
- Son olarak, dönme merkezini ait olduğu yere geri çevirin.