Bilgisayar Grafiği - Hızlı Kılavuz

Bilgisayar grafikleri, bilgisayar ekranlarında programlama yardımı ile resim çizme sanatıdır. Verilerin hesaplanmasını, oluşturulmasını ve değiştirilmesini içerir. Başka bir deyişle, bilgisayar grafiklerinin görüntülerin oluşturulması ve manipülasyonu için bir işleme aracı olduğunu söyleyebiliriz.

Katot Işın Tüpü

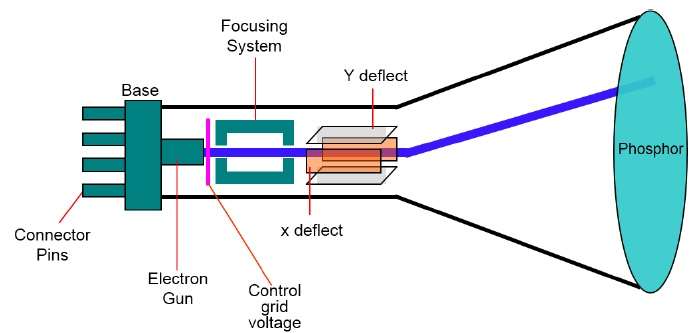
Bir grafik sistemdeki birincil çıkış cihazı video monitörüdür. Bir video monitörünün ana öğesi,Cathode Ray Tube (CRT), aşağıdaki şekilde gösterilmiştir.

CRT'nin çalışması çok basittir -

• Elektron tabancası bir elektron ışını (katot ışınları) yayar.

• Elektron ışını, onu fosfor kaplı ekran üzerinde belirli konumlara yönlendiren odaklama ve saptırma sistemlerinden geçer.

• Işın ekrana çarptığında, fosfor elektron ışınının temas ettiği her konumda küçük bir ışık noktası yayar.

• Elektron ışınını aynı ekran noktalarına hızla geri yönlendirerek resmi yeniden çizer.

Ekranda bir nesneyi görüntülemenin iki yolu vardır (Rastgele tarama ve Raster tarama).

Raster Tarama

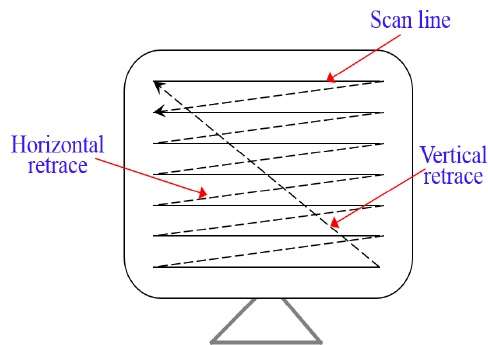
Bir raster tarama sisteminde, elektron ışını ekran boyunca yukarıdan aşağıya doğru birer birer taranır. Elektron ışını her sıra boyunca hareket ederken, ışıklı noktaların bir modelini oluşturmak için ışın yoğunluğu açılır ve kapanır.

Resim tanımı, adı verilen hafıza alanında saklanır. Refresh Buffer veya Frame Buffer. Bu bellek alanı, tüm ekran noktaları için yoğunluk değerleri kümesini tutar. Depolanan yoğunluk değerleri daha sonra yenileme arabelleğinden alınır ve aşağıdaki şekilde gösterildiği gibi her seferinde bir satır (tarama çizgisi) ekranda "boyanır".

Her bir tarama noktası, bir pixel (picture element) veya pel. Her tarama çizgisinin sonunda, elektron ışını, sonraki tarama çizgisini görüntülemeye başlamak için ekranın sol tarafına döner.

Rastgele Tarama (Vektör Tarama)

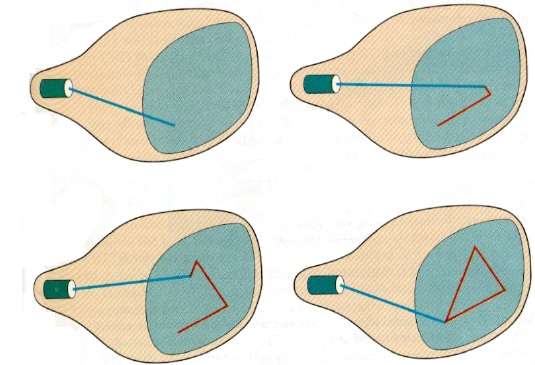
Bu teknikte, elektron ışını, raster taramada olduğu gibi soldan sağa ve yukarıdan aşağıya taramak yerine, ekranın yalnızca resmin çizileceği kısmına yönlendirilir. Aynı zamandavector display, stroke-writing display, veya calligraphic display.

Resim tanımı, bir dizi çizgi çizim komutları olarak anılan hafıza alanında saklanır. refresh display file. Belirli bir resmi görüntülemek için, sistem, her bir bileşen çizgisini sırayla çizerek, görüntüleme dosyasındaki komutlar kümesi arasında geçiş yapar. Tüm çizgi çizme komutları işlendikten sonra, sistem listedeki ilk satır komutuna geri döner.

Rastgele tarama görüntüleri, bir resmin tüm bileşen çizgilerini saniyede 30 ila 60 kez çizecek şekilde tasarlanmıştır.

Bilgisayar Grafiklerinin Uygulanması

Computer Graphics, bazıları aşağıda listelenen çok sayıda uygulamaya sahiptir -

• Computer graphics user interfaces (GUIs) - Kullanıcının bir bilgisayarla etkileşime girmesine olanak tanıyan grafik, fare odaklı bir paradigma.

• Business presentation graphics - "Bir resim bin kelimeye bedeldir".

• Cartography - Harita çizimi.

• Weather Maps - Gerçek zamanlı haritalama, sembolik temsiller.

• Satellite Imaging - Jeodezik görüntüler.

• Photo Enhancement - Bulanık fotoğrafları netleştirme.

• Medical imaging - MRI'lar, CAT taramaları, vb. - Non-invaziv dahili muayene.

• Engineering drawings - mekanik, elektrik, inşaat vb. - Geçmişin planlarını değiştirmek.

• Typography - Yayıncılıkta karakter imgelerinin kullanımı - geçmişin sert tipinin yerini alıyor.

• Architecture - İnşaat planları, dış eskizler - geçmişin planlarını ve el çizimlerini değiştirmek.

• Art - Bilgisayarlar sanatçılar için yeni bir ortam sağlar.

• Training - Uçuş simülatörleri, bilgisayar destekli talimat vb.

• Entertainment - Filmler ve oyunlar.

• Simulation and modeling - Fiziksel modelleme ve canlandırmaların değiştirilmesi

Bir çizgi iki noktayı birleştirir. Grafikte temel bir unsurdur. Bir çizgi çizmek için, aralarına çizgi çizebileceğiniz iki noktaya ihtiyacınız vardır. Aşağıdaki üç algoritmada, çizginin bir noktasını şöyle adlandırıyoruz$X_{0}, Y_{0}$ ve çizginin ikinci noktası $X_{1}, Y_{1}$.

DDA Algoritması

Sayısal Diferansiyel Analiz (DDA) algoritması, burada adım adım açıklanan basit hat oluşturma algoritmasıdır.

Step 1 - İki uç noktanın girdisini alın $(X_{0}, Y_{0})$ ve $(X_{1}, Y_{1})$.

Step 2 - İki uç nokta arasındaki farkı hesaplayın.

dx = X1 - X0
dy = Y1 - Y0

Step 3- 2. adımda hesaplanan farka bağlı olarak, piksel koymak için adım sayısını belirlemeniz gerekir. Dx> dy ise, x koordinatında daha fazla adıma ihtiyacınız vardır; aksi takdirde y koordinatında.

if (absolute(dx) > absolute(dy))
   Steps = absolute(dx);
else
   Steps = absolute(dy);

Step 4 - x koordinatı ve y koordinatındaki artışı hesaplayın.

Xincrement = dx / (float) steps;
Yincrement = dy / (float) steps;

Step 5 - x ve y koordinatlarını uygun şekilde artırarak pikseli yerleştirin ve çizginin çizimini tamamlayın.

for(int v=0; v < Steps; v++)
{
   x = x + Xincrement;
   y = y + Yincrement;
   putpixel(Round(x), Round(y));
}

Bresenham'ın Hat Üretimi

Bresenham algoritması, başka bir artımlı tarama dönüştürme algoritmasıdır. Bu algoritmanın en büyük avantajı, yalnızca tamsayı hesaplamaları kullanmasıdır. X ekseni boyunca birim aralıklarla hareket edin ve her adımda iki farklı y koordinatı arasından seçim yapın.

Örneğin, aşağıdaki çizimde gösterildiği gibi, (2, 3) konumundan (3, 3) ve (3, 4) arasından seçim yapmanız gerekir. Orijinal çizgiye daha yakın olan noktayı istersiniz.

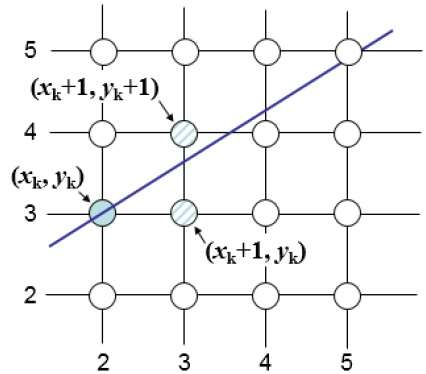
Örnek pozisyonda $X_{k}+1,$ matematiksel çizgiden dikey ayrımlar şu şekilde etiketlenir: $d_{upper}$ ve $d_{lower}$.

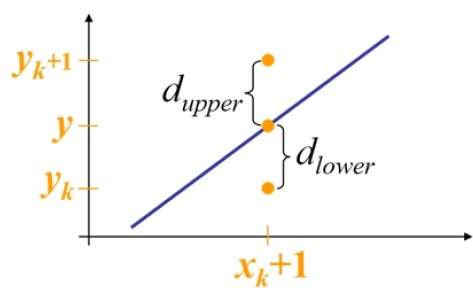
Yukarıdaki çizimden, matematiksel doğrudaki y koordinatı $x_{k}+1$ -

Y = m ($X_{k}$+1) + b

Yani, $d_{upper}$ ve $d_{lower}$ aşağıdaki gibi verilmiştir -

$$d_{lower} = y-y_{k}$$

$$= m(X_{k} + 1) + b - Y_{k}$$

ve

$$d_{upper} = (y_{k} + 1) - y$$

$= Y_{k} + 1 - m (X_{k} + 1) - b$

Bunları hangi pikselin matematiksel çizgiye daha yakın olduğuna dair basit bir karar vermek için kullanabilirsiniz. Bu basit karar, iki piksel konumu arasındaki farka dayanmaktadır.

$$d_{lower} - d_{upper} = 2m(x_{k} + 1) - 2y_{k} + 2b - 1$$

Bize yerine olsun m ile dy / dx burada dx ve dy son noktaları arasındaki farklar bulunmaktadır.

$$dx (d_{lower} - d_{upper}) =dx(2\frac{\mathrm{d} y}{\mathrm{d} x}(x_{k} + 1) - 2y_{k} + 2b - 1)$$

$$ = 2dy.x_{k} - 2dx.y_{k} + 2dy + 2dx(2b-1)$$

$$ = 2dy.x_{k} - 2dx.y_{k} + C$$

Yani bir karar parametresi $P_{k}$için k bir hat boyunca inci adım verilir -

$$p_{k} = dx(d_{lower} - d_{upper})$$

$$ = 2dy.x_{k} - 2dx.y_{k} + C$$

Karar parametresinin işareti $P_{k}$ ile aynı $d_{lower} - d_{upper}$.

Eğer $p_{k}$ negatifse alt pikseli seçin, aksi takdirde üst pikseli seçin.

Unutmayın, koordinat değişiklikleri x ekseni boyunca birim adımlarla gerçekleşir, böylece her şeyi tam sayı hesaplamalarıyla yapabilirsiniz. K + 1 adımında, karar parametresi şu şekilde verilir -

$$p_{k +1} = 2dy.x_{k + 1} - 2dx.y_{k + 1} + C$$

Çıkarma $p_{k}$ bundan anlıyoruz -

$$p_{k + 1} - p_{k} = 2dy(x_{k + 1} - x_{k}) - 2dx(y_{k + 1} - y_{k})$$

Fakat, $x_{k+1}$ aynıdır $x_{k+1}$. Yani -

$$p_{k+1} = p_{k} + 2dy - 2dx(y_{k+1} - y_{k})$$

Nerede, $Y_{k+1} – Y_{k}$ işaretine bağlı olarak 0 veya 1'dir $P_{k}$.

İlk karar parametresi $p_{0}$ değerlendirilir $(x_{0}, y_{0})$ olarak verilir -

$$p_{0} = 2dy - dx$$

Şimdi, yukarıdaki tüm noktaları ve hesaplamaları göz önünde bulundurarak, işte m <1 eğimi için Bresenham algoritması -

Step 1 - Sol uç noktayı buraya kaydederek, çizginin iki bitiş noktasını girin. $(x_{0}, y_{0})$.

Step 2 - Noktayı çizin $(x_{0}, y_{0})$.

Step 3 - dx, dy, 2dy ve (2dy - 2dx) sabitlerini hesaplayın ve karar parametresi için ilk değeri şu şekilde alın:

$$p_{0} = 2dy - dx$$

Step 4 - Her birinde $X_{k}$ çizgi boyunca, k = 0'dan başlayarak aşağıdaki testi gerçekleştirin -

Eğer $p_{k}$ <0, arsa için sonraki nokta $(x_{k}+1, y_{k})$ ve

$$p_{k+1} = p_{k} + 2dy$$ Aksi takdirde,

$$(x_{k}, y_{k}+1)$$

$$p_{k+1} = p_{k} + 2dy - 2dx$$

Step 5 - 4. adımı (dx - 1) kez tekrarlayın.

M> 1 için, her seferinde y'yi artırırken x'i artırmanız gerekip gerekmediğini öğrenin.

Çözdükten sonra karar parametresi için denklem $P_{k}$ çok benzer olacaktır, sadece denklemdeki x ve y birbirinin yerine geçer.

Orta Nokta Algoritması

Orta nokta algoritması, Pitteway ve Van Aken tarafından modifiye edilen Bresenham'dan kaynaklanmaktadır. P noktasını (x, y) koordinatına zaten koyduğunuzu ve aşağıdaki şekilde gösterildiği gibi doğrunun eğiminin 0 ≤ k ≤ 1 olduğunu varsayalım.

Şimdi bir sonraki noktayı E'ye mi yoksa N'ye mi koyacağınıza karar vermelisiniz. Bu, N veya E noktasına en yakın Q kesişme noktasını belirleyerek seçilebilir. Q kesişme noktası N noktasına en yakınsa, N olarak kabul edilir. sonraki nokta; aksi takdirde E.

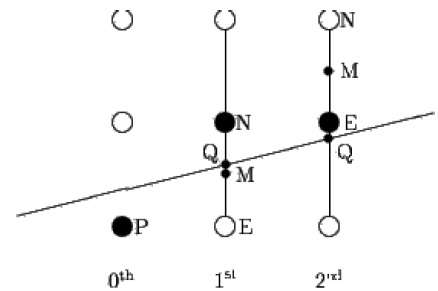
Bunu belirlemek için önce orta noktayı M (x + 1, y + ½) hesaplayın. E ve N'yi birleştiren dikey çizgi ile çizginin Q kesişme noktası M'nin altındaysa, bir sonraki nokta olarak E'yi alın; aksi takdirde bir sonraki nokta olarak N'yi alın.

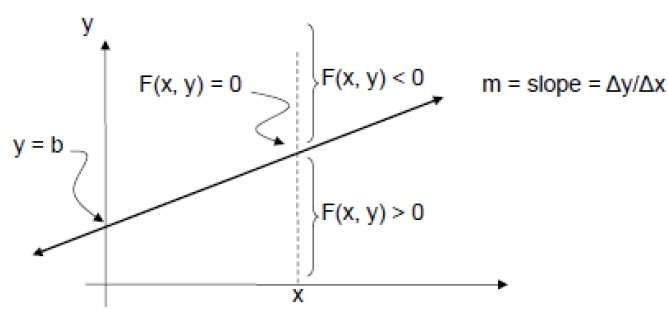
Bunu kontrol etmek için örtük denklemi dikkate almalıyız -

F (x, y) = mx + b - y

Herhangi bir X'de pozitif m için,

• Y satır üzerindeyse, F (x, y) = 0
• Y çizginin üstündeyse, F (x, y) <0
• Y çizginin altındaysa, F (x, y)> 0

Ekranda daire çizmek, çizgi çizmekten biraz daha karmaşıktır. Bir daire oluşturmak için iki popüler algoritma vardır -Bresenham’s Algorithm ve Midpoint Circle Algorithm. Bu algoritmalar, daireyi çizmek için gerekli olan sonraki noktaları belirleme fikrine dayanmaktadır. Algoritmaları ayrıntılı olarak tartışalım -

Çemberin denklemi $X^{2} + Y^{2} = r^{2},$ burada r yarıçaptır.

Bresenham Algoritması

Tarama ekranında sürekli bir yay görüntüleyemiyoruz. Bunun yerine yayı tamamlamak için en yakın piksel konumunu seçmeliyiz.

Aşağıdaki resimden, pikseli (X, Y) konumuna koyduğumuzu ve şimdi bir sonraki pikseli nereye koyacağımıza karar vermemiz gerektiğini görebilirsiniz - N (X + 1, Y) veya S (X + 1, Y-1).

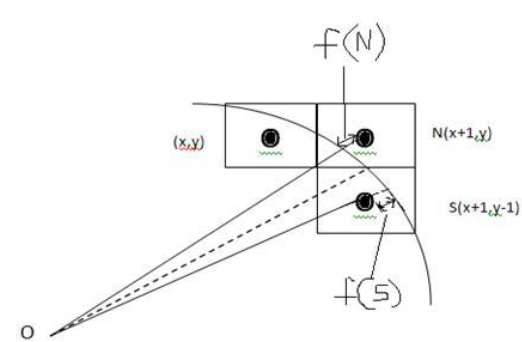
Buna karar parametresi ile karar verilebilir d.

• D <= 0 ise, sonraki piksel olarak N (X + 1, Y) seçilecektir.
• D> 0 ise, sonraki piksel olarak S (X + 1, Y-1) seçilecektir.

Algoritma

Step 1- Çemberin ve yarıçapın merkezinin koordinatlarını alın ve bunları sırasıyla x, y ve R'de saklayın. P = 0 ve Q = R olarak ayarlayın.

Step 2 - Karar parametresi D = 3 - 2R'yi ayarlayın.

Step 3 - P ≤ Q iken 8. adımı tekrarlayın.

Step 4 - Draw Circle (X, Y, P, Q) arayın.

Step 5 - P'nin değerini artırın.

Step 6 - D <0 ise D = D + 4P + 6.

Step 7 - Başka Küme R = R - 1, D = D + 4 (PQ) + 10.

Step 8 - Draw Circle (X, Y, P, Q) arayın.

Draw Circle Method(X, Y, P, Q).

Call Putpixel (X + P, Y + Q).
Call Putpixel (X - P, Y + Q).
Call Putpixel (X + P, Y - Q).
Call Putpixel (X - P, Y - Q).
Call Putpixel (X + Q, Y + P).
Call Putpixel (X - Q, Y + P).
Call Putpixel (X + Q, Y - P).
Call Putpixel (X - Q, Y - P).

Orta Nokta Algoritması

Step 1 - Giriş yarıçapı r ve daire merkezi $(x_{c,} y_{c})$ ve başlangıç ​​noktasında ortalanmış dairenin çevresi üzerindeki ilk noktayı şu şekilde elde edin:

(x0, y0) = (0, r)

Step 2 - Karar parametresinin başlangıç ​​değerini şu şekilde hesaplayın:

$P_{0}$ = 5/4 - r (Bu denklemin basitleştirilmesi için aşağıdaki açıklamaya bakın.)

f(x, y) = x2 + y2 - r2 = 0

f(xi - 1/2 + e, yi + 1)
        = (xi - 1/2 + e)2 + (yi + 1)2 - r2 
        = (xi- 1/2)2 + (yi + 1)2 - r2 + 2(xi - 1/2)e + e2
        = f(xi - 1/2, yi + 1) + 2(xi - 1/2)e + e2 = 0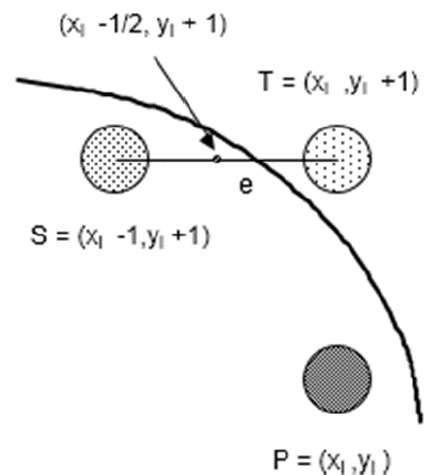

Let di = f(xi - 1/2, yi + 1) = -2(xi - 1/2)e - e2
Thus,

If e < 0 then di > 0 so choose point S = (xi - 1, yi + 1).
di+1    = f(xi - 1 - 1/2, yi + 1 + 1) = ((xi - 1/2) - 1)2 + ((yi + 1) + 1)2 - r2
        = di - 2(xi - 1) + 2(yi + 1) + 1
        = di + 2(yi + 1 - xi + 1) + 1
		  
If e >= 0 then di <= 0 so choose point T = (xi, yi + 1)
   di+1 = f(xi - 1/2, yi + 1 + 1)
       = di + 2yi+1 + 1
		  
The initial value of di is
   d0 = f(r - 1/2, 0 + 1) = (r - 1/2)2 + 12 - r2
      = 5/4 - r {1-r can be used if r is an integer}
		
When point S = (xi - 1, yi + 1) is chosen then
   di+1 = di + -2xi+1 + 2yi+1 + 1
	
When point T = (xi, yi + 1) is chosen then
   di+1 = di + 2yi+1 + 1

Step 3 - Her birinde $X_{K}$ K = 0'dan başlayan konum, aşağıdaki testi gerçekleştirin -

If PK < 0 then next point on circle (0,0) is (XK+1,YK) and
   PK+1 = PK + 2XK+1 + 1
Else
   PK+1 = PK + 2XK+1 + 1 – 2YK+1
	
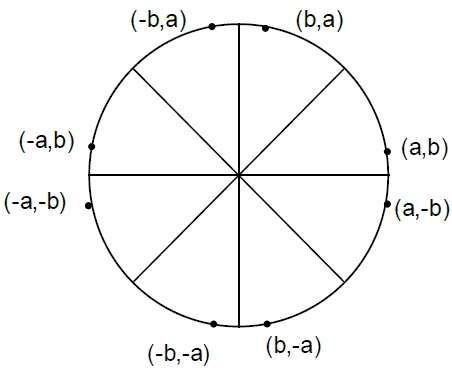
Where, 2XK+1 = 2XK+2 and 2YK+1 = 2YK-2.

Step 4 - Diğer yedi oktttaki simetri noktalarını belirleyin.

Step 5 - Hesaplanan her piksel konumunu (X, Y) ortalanmış dairesel yola taşıyın $(X_{C,} Y_{C})$ ve koordinat değerlerini çizin.

X = X + XC,   Y = Y + YC

Step 6 - X> = Y olana kadar 3. ila 5. adımları tekrarlayın.

Çokgen, aşağıdaki şekilde gösterildiği gibi sıralı bir köşe noktası listesidir. Çokgenleri belirli renklerle doldurmak için, çokgenin sınırına düşen pikselleri ve çokgenin içine düşenleri belirlemeniz gerekir. Bu bölümde, çokgenleri farklı teknikler kullanarak nasıl doldurabileceğimizi göreceğiz.

Tarama Çizgisi Algoritması

Bu algoritma, tarama çizgisini çokgen kenarlarla keserek çalışır ve çokgeni kesişim çiftleri arasında doldurur. Aşağıdaki adımlar, bu algoritmanın nasıl çalıştığını göstermektedir.

Step 1 - Verilen çokgenden Ymin ve Ymax'ı bulun.

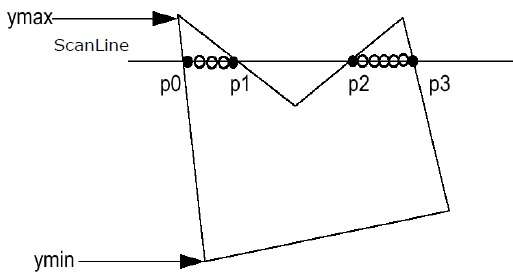
Step 2- ScanLine, Ymin'den Ymax'a kadar poligonun her kenarıyla kesişir. Çokgenin her kesişme noktasını adlandırın. Yukarıda gösterilen şekle göre p0, p1, p2, p3 olarak adlandırılırlar.

Step 3 - Kesişme noktasını artan X koordinatına göre sıralayın, yani (p0, p1), (p1, p2) ve (p2, p3).

Step 4 - Çokgenlerin içindeki tüm koordinat çiftlerini doldurun ve alternatif çiftleri göz ardı edin.

Taşkın Doldurma Algoritması

Bazen alanı ve sınırını farklı renklerle doldurmak istediğimiz bir nesneye rastlıyoruz. Bu tür nesneleri, sınır doldurma algoritmasında olduğu gibi belirli bir sınır rengini aramak yerine belirli bir iç renkle boyayabiliriz.

Nesnenin sınırına güvenmek yerine, dolgu rengine güvenir. Başka bir deyişle, nesnenin iç rengini dolgu rengiyle değiştirir. Orijinal iç rengin artık pikselleri kalmadığında, algoritma tamamlanır.

Bir kez daha, bu algoritma pikselleri doldurmak için Four-connect veya Sekiz-bağlantı yöntemine dayanır. Ancak sınır rengini aramak yerine, iç mekanın bir parçası olan tüm bitişik pikselleri arıyor.

Sınır Doldurma Algoritması

Sınır doldurma algoritması, adı olarak çalışır. Bu algoritma, bir nesnenin içindeki bir noktayı seçer ve nesnenin sınırına ulaşana kadar doldurmaya başlar. Bu algoritmanın çalışması için sınırın rengi ve doldurduğumuz renk farklı olmalıdır.

Bu algoritmada, sınırın renginin tüm nesne için aynı olduğunu varsayıyoruz. Sınır doldurma algoritması 4 bağlantılı pikseller veya 8 bağlantılı pikseller ile uygulanabilir.

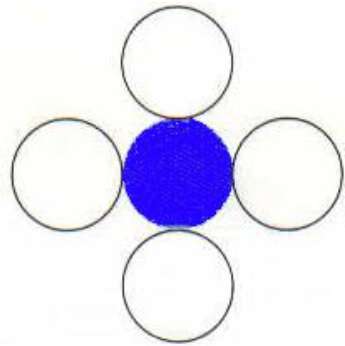
4 Bağlantılı Çokgen

Bu teknikte şekilde gösterildiği gibi 4 bağlantılı pikseller kullanılır. Pikselleri mevcut piksellerin üstüne, altına, sağına ve soluna koyuyoruz ve bu işlem farklı renkte bir sınır bulana kadar devam edecek.

Algoritma

Step 1 - Tohum noktası (seedx, seedy), fcolor ve dcol değerini başlatın.

Step 2 - Poligonun sınır değerlerini tanımlayın.

Step 3 - Geçerli tohum noktasının varsayılan renk olup olmadığını kontrol edin, ardından sınır piksellerine ulaşana kadar 4. ve 5. adımları tekrarlayın.

If getpixel(x, y) = dcol then repeat step 4 and 5

Step 4 - Tohum noktasındaki dolgu rengiyle varsayılan rengi değiştirin.

setPixel(seedx, seedy, fcol)

Step 5 - Prosedürü dört mahalle noktasıyla yinelemeli olarak izleyin.

FloodFill (seedx – 1, seedy, fcol, dcol)
FloodFill (seedx + 1, seedy, fcol, dcol)
FloodFill (seedx, seedy - 1, fcol, dcol)
FloodFill (seedx – 1, seedy + 1, fcol, dcol)

Step 6 - Çıkış

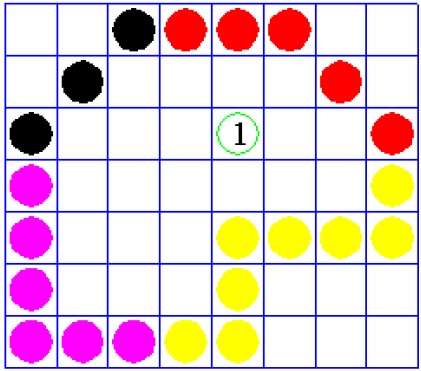
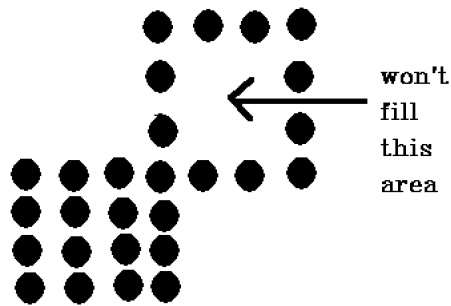
Bu teknikte bir sorun var. Tüm bölgeyi doldurmaya çalıştığımız durumu aşağıda gösterilen şekilde düşünün. Burada görüntü sadece kısmen doldurulur. Bu gibi durumlarda 4 bağlantılı piksel tekniği kullanılamaz.

8-Bağlı Çokgen

Bu teknikte şekilde gösterildiği gibi 8 bağlantılı pikseller kullanılır. 4 bağlantılı teknikte yaptığımız gibi pikselleri mevcut piksellerin üstüne, altına, sağına ve soluna koyuyoruz.

Buna ek olarak, mevcut pikselin tüm alanı kapsanacak şekilde pikselleri köşegenlere de yerleştiriyoruz. Bu süreç farklı renkte bir sınır bulana kadar devam edecek.

Algoritma

Step 1 - Tohum noktası (seedx, seedy), fcolor ve dcol değerini başlatın.

Step 2 - Poligonun sınır değerlerini tanımlayın.

Step 3 - Geçerli tohum noktasının varsayılan renk olup olmadığını kontrol edin, ardından sınır piksellerine ulaşana kadar 4. ve 5. adımları tekrarlayın

If getpixel(x,y) = dcol then repeat step 4 and 5

Step 4 - Tohum noktasındaki dolgu rengiyle varsayılan rengi değiştirin.

setPixel(seedx, seedy, fcol)

Step 5 - Prosedürü dört mahalle noktasıyla yinelemeli olarak izleyin

FloodFill (seedx – 1, seedy, fcol, dcol)
FloodFill (seedx + 1, seedy, fcol, dcol)
FloodFill (seedx, seedy - 1, fcol, dcol)
FloodFill (seedx, seedy + 1, fcol, dcol)
FloodFill (seedx – 1, seedy + 1, fcol, dcol)
FloodFill (seedx + 1, seedy + 1, fcol, dcol)
FloodFill (seedx + 1, seedy - 1, fcol, dcol)
FloodFill (seedx – 1, seedy - 1, fcol, dcol)

Step 6 - Çıkış

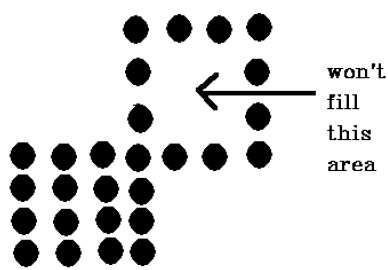
4 bağlantılı piksel tekniği, 8 bağlantılı teknikte olmayacak şekilde aşağıdaki şekilde işaretlenen alanı doldurmayı başaramadı.

İç-Dış Test

Bu yöntem aynı zamanda counting number method. Bir nesneyi doldururken, genellikle belirli bir noktanın nesnenin içinde mi yoksa dışında mı olduğunu belirlememiz gerekir. Belirli bir noktanın bir nesnenin içinde mi yoksa dışında mı olduğunu belirleyebileceğimiz iki yöntem vardır.

• Tek-Çift Kuralı
• Sıfır olmayan sargı numarası kuralı

Tek-Çift Kuralı

Bu teknikte, çizgi boyunca herhangi bir noktadan (x, y) sonsuza kadar geçen kenarı sayarız. Etkileşim sayısı tekse (x, y) noktası bir iç noktadır. Etkileşim sayısı çift ise, nokta (x, y) bir dış noktadır. İşte size net bir fikir verecek örnek -

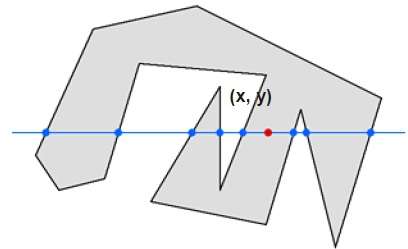
Yukarıdaki şekilden, (x, y) noktasından, sol taraftaki etkileşim noktası sayısının 5 ve sağ taraftaki etkileşim noktasının 3 olduğunu görebiliriz. Yani toplam etkileşim noktası sayısı 8'dir ki bu tek sayıdır. . Bu nedenle nokta, nesne içinde değerlendirilir.

Sıfır Olmayan Sargı Numarası Kuralı

Bu yöntem, verilen noktanın iç olup olmadığını test etmek için basit çokgenlerle de kullanılır. Bir pim ve bir lastik bant yardımıyla basitçe anlaşılabilir. Pimi poligonun kenarlarından birine sabitleyin ve lastik bandı buna bağlayın ve ardından lastik bandı poligonun kenarları boyunca gerdirin.

Poligonun tüm kenarları lastik bantla kaplandığında, test edilecek noktada sabitlenmiş olan pimi kontrol edin. Poligon içinde düşündüğümüz noktada en az bir rüzgar bulursak, aksi takdirde noktanın poligonun içinde olmadığını söyleyebiliriz.

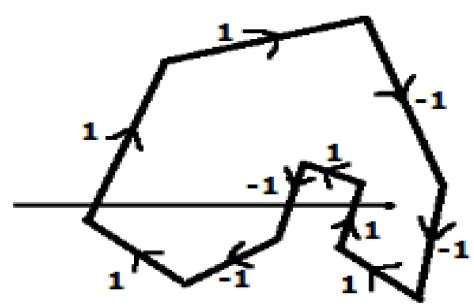
Başka bir alternatif yöntemde, çokgenin tüm kenarlarına yön verin. Test edilecek noktadan X yönünün en soluna doğru bir tarama çizgisi çizin.

• Yukarı doğru giden tüm kenarlara 1 değerini ve yön değeri olarak tüm diğer -1 değerini verin.

• Tarama çizgisinin içinden geçtiği kenar yönü değerlerini kontrol edin ve toplayın.

• Bu yön değerinin toplam toplamı sıfır değilse, test edilecek bu nokta bir interior point, aksi halde bir exterior point.

• Yukarıdaki şekilde, tarama hattının geçtiği yön değerlerini topluyoruz ve ardından toplam 1 - 1 + 1 = 1; sıfır olmayan. Yani noktanın bir iç nokta olduğu söyleniyor.

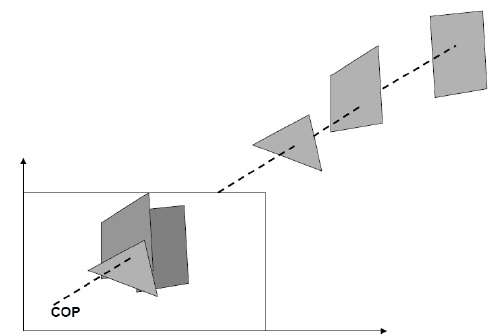
Bilgisayar grafiklerinde kırpmanın birincil kullanımı, görüntüleme bölmesinin dışındaki nesneleri, çizgileri veya çizgi parçalarını kaldırmaktır. Görüntüleme dönüşümü, izleme hacmine göre noktaların konumuna - özellikle izleyicinin arkasındaki noktalara - duyarsızdır ve görünümü oluşturmadan önce bu noktaların kaldırılması gerekir.

Nokta Kırpma

Belirli bir pencereden bir noktayı kırpmak çok kolaydır. Dikdörtgenin pencereyi gösterdiği aşağıdaki şekli düşünün. Nokta kırpma bize verilen noktanın (X, Y) verilen pencere içinde olup olmadığını söyler; ve pencerenin minimum ve maksimum koordinatlarını kullanıp kullanmayacağımıza karar verir.

X, Wx1 ≤ X ≤ Wx2 arasında yer alıyorsa, verilen noktanın X koordinatı pencerenin içindedir. Aynı şekilde, Y Wy1 ≤ Y ≤ Wy2 arasında yer alıyorsa, verilen noktanın Y koordinatı pencerenin içindedir.

Çizgi Kırpma

Çizgi kırpma kavramı, nokta kırpma ile aynıdır. Çizgi kırpmada, çizginin pencere dışında kalan kısmını keseceğiz ve sadece pencere içinde kalan kısmı tutacağız.

Cohen-Sutherland Hat Küpürleri

Bu algoritma, aşağıdaki şekilde gösterildiği gibi kırpma penceresini kullanır. Kırpma bölgesi için minimum koordinat$(XW_{min,} YW_{min})$ ve kırpma bölgesi için maksimum koordinat $(XW_{max,} YW_{max})$.

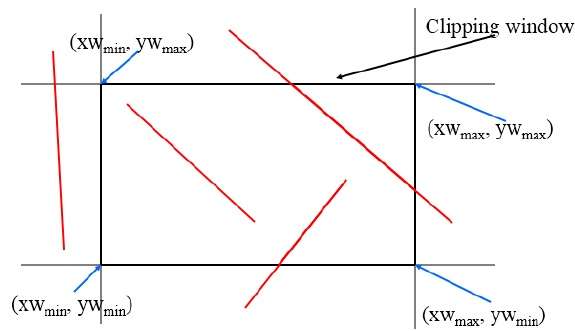
Tüm bölgeyi bölmek için 4 bit kullanacağız. Bu 4 bit, aşağıdaki şekilde gösterildiği gibi bölgenin Üst, Alt, Sağ ve Solunu temsil eder. BuradaTOP ve LEFT bit 1 olarak ayarlanmıştır çünkü TOP-LEFT köşe.

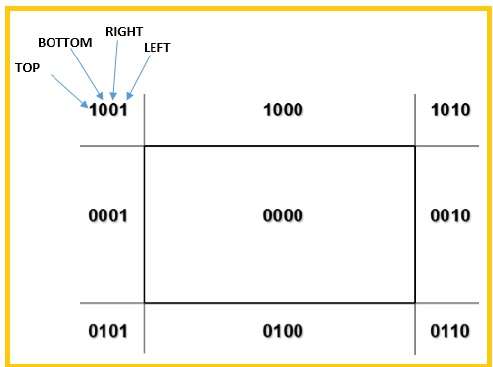
Hat için 3 olasılık vardır -

• Satır tamamen pencere içinde olabilir (Bu satır kabul edilmelidir).

• Satır tamamen pencere dışında olabilir (Bu satır bölgeden tamamen kaldırılacaktır).

• Çizgi kısmen pencerenin içinde olabilir (Kesişme noktasını bulacağız ve çizginin sadece bölgenin içindeki kısmını çizeceğiz).

Algoritma

Step 1 - Her uç nokta için bir bölge kodu atayın.

Step 2 - Her iki uç noktanın da bölge kodu varsa 0000 sonra bu satırı kabul edin.

Step 3 - Aksi takdirde, mantıklı yapın ANDher iki bölge kodu için işlem.

Step 3.1 - Sonuç değilse 0000, sonra hattı reddedin.

Step 3.2 - Aksi halde kırpmaya ihtiyacın var.

Step 3.2.1 - Pencerenin dışındaki çizginin bir uç noktasını seçin.

Step 3.2.2 - Pencere sınırındaki kesişme noktasını bulun (bölge koduna göre).

Step 3.2.3 - Uç noktayı kesişim noktasıyla değiştirin ve bölge kodunu güncelleyin.

Step 3.2.4 - Önemsiz bir şekilde kabul edilen veya önemsiz bir şekilde reddedilen kırpılmış bir çizgi bulana kadar 2. adımı tekrarlayın.

Step 4 - Diğer satırlar için 1. adımı tekrarlayın.

Cyrus-Beck Çizgi Kırpma Algoritması

Bu algoritma, Cohen-Sutherland algoritmasından daha etkilidir. Parametrik çizgi gösterimini ve basit nokta ürünlerini kullanır.

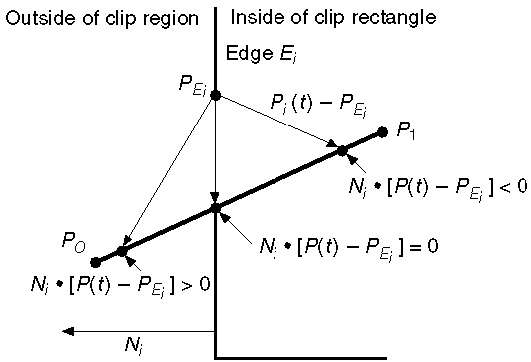
Doğrunun parametrik denklemi -

P0P1:P(t) = P0 + t(P1-P0)

N _i dışa doğru normal kenar E _{i olsun} . Şimdi E _i kenarındaki herhangi bir rastgele noktayı P _{Ei seçin} ve ardından nokta çarpımı N _i ∙ [P (t) - P _Ei ], P (t) noktasının "klips kenarının içinde" mi yoksa "dışında" mı olduğunu belirler Klip kenarında "açık".

N _i ise P (t) noktası içerdedir . [P (t) - P _Ei ] <0

N _i ise P (t) noktası dışarıdadır . [P (t) - P _Ei ]> 0

N _i ise P (t) noktası _kenardadır . [P (t) - P _Ei ] = 0 (Kesişme noktası)

N _ben . [P (t) - P _Ei ] = 0

N _i . [P ₀ + t (P _1- P ₀ ) - P _Ei ] = 0 (P (t) yerine P ₀ + t (P _1- P ₀ ))

N _i . [P ₀ - P _Ei ] + N _i .t [P _1- P ₀ ] = 0

N _i . [P ₀ - P _Ei ] + N _i ∙ tD = 0 ([P _1- P ₀ ] yerine D yerine geçerek )

N _ben . [P ₀ - P _Ei ] = - N _ben ∙ tD

T'nin denklemi,

$$t = \tfrac{N_{i}.[P_{o} - P_{Ei}]}{{- N_{i}.D}}$$

Aşağıdaki koşullar için geçerlidir -

• N _i ≠ 0 (hata olamaz)
• D ≠ 0 (P ₁ ≠ P ₀ )
• N _ben ∙ D ≠ 0 (P ₀ P ₁ E _i'ye paralel değil )

Çokgen Kırpma (Sutherland Hodgman Algoritması)

Bir çokgen, kırpma penceresi belirlenerek de kırpılabilir. Poligon kırpma için Sutherland Hodgeman poligon kırpma algoritması kullanılmıştır. Bu algoritmada, çokgenin tüm köşeleri, kırpma penceresinin her bir kenarına doğru kırpılır.

İlk önce, çokgenin yeni köşelerini elde etmek için çokgen, çokgen penceresinin sol kenarına doğru kırpılır. Bu yeni köşeler, aşağıdaki şekilde gösterildiği gibi çokgeni kırpma penceresinin sağ kenarına, üst kenarına, alt kenarına kırpmak için kullanılır.

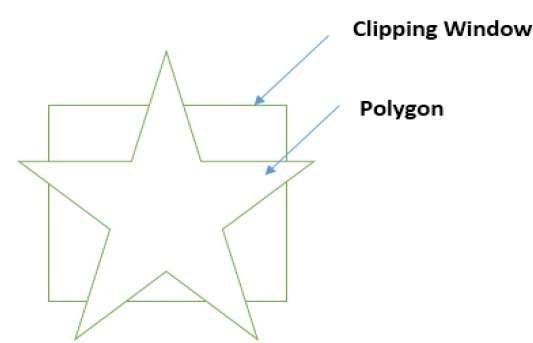
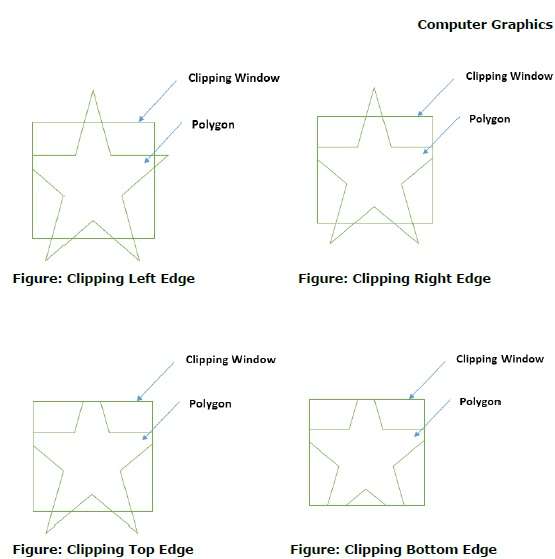
Kırpma pencereli bir çokgenin bir kenarını işlerken, kenar tamamen kırpma penceresinin içinde değilse ve kesişme noktasından dış kenara kısmi bir kenar kırpılmışsa bir kesişim noktası bulunur. Aşağıdaki şekiller sol, sağ, üst ve alt kenar kesmelerini göstermektedir -

Metin Kırpma

Bir bilgisayar grafiğinde metin kırpma sağlamak için çeşitli teknikler kullanılır. Karakterleri oluşturmak için kullanılan yöntemlere ve belirli bir uygulamanın gereksinimlerine bağlıdır. Aşağıda listelenen üç metin kırpma yöntemi vardır -

• Tümü veya hiçbiri dize kırpma
• Tümü veya hiçbiri karakter kırpma
• Metin kırpma

Aşağıdaki şekil dize kırpmanın tamamını veya hiçbirini göstermez -

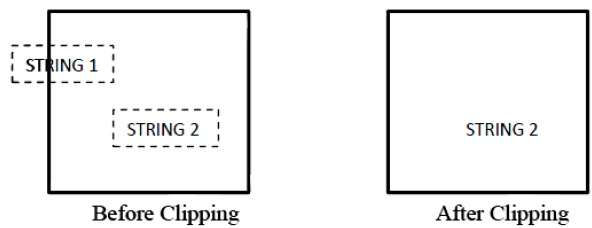
Tümü veya hiçbiri dizge kırpma yönteminde, dizenin tamamını tutarız veya tüm dizeyi kırpma penceresine göre reddederiz. Yukarıdaki şekilde gösterildiği gibi, STRING2 tamamen kırpma penceresinin içinde olduğundan onu tutuyoruz ve STRING1 sadece kısmen pencerenin içinde kalıyor, reddediyoruz.

Aşağıdaki şekil, karakter kırpmanın tümünü veya hiçbirini göstermez -

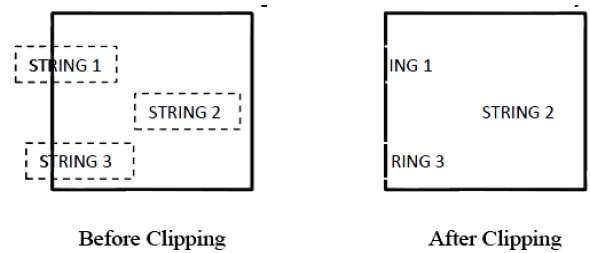
Bu kırpma yöntemi dizenin tamamı yerine karakterlere dayanmaktadır. Bu yöntemde dizge tamamen kırpma penceresinin içindeyse, onu saklarız. Kısmen pencerenin dışındaysa, o zaman -

• İpin sadece dışarıdaki kısmını reddediyorsunuz

• Karakter, kırpma penceresinin sınırındaysa, o karakterin tamamını atarız ve kalan dizeyi saklarız.

Aşağıdaki şekil metin kırpmayı göstermektedir -

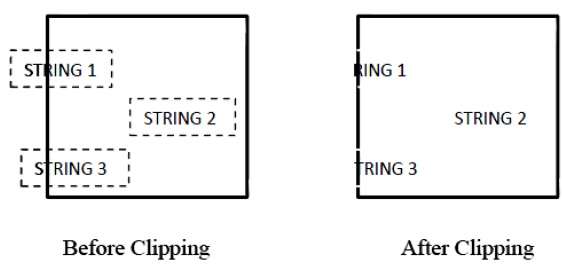
Bu kırpma yöntemi dizenin tamamı yerine karakterlere dayanmaktadır. Bu yöntemde dizge tamamen kırpma penceresinin içindeyse, onu saklarız. Kısmen pencerenin dışındaysa, o zaman

• İpin sadece dışarıdaki kısmını reddediyorsunuz.

• Karakter, kırpma penceresinin sınırındaysa, o zaman karakterin yalnızca kırpma penceresinin dışında kalan kısmını atarız.

Bitmap Grafikleri

Bir bitmap, bir görüntüyü tanımlayan bir pikseller koleksiyonudur. Bilgisayarın resimleri saklamak ve görüntülemek için kullandığı bir bilgisayar grafiği türüdür. Bu tür grafiklerde, görüntüler parça parça saklanır ve bu nedenle Bit-harita grafikleri olarak adlandırılır. Daha iyi anlamak için, bit harita grafiklerini kullanarak gülen yüz çizdiğimiz aşağıdaki örneği ele alalım.

Şimdi bu gülen yüzün bilgisayar grafiklerinde parça parça nasıl saklandığını göreceğiz.

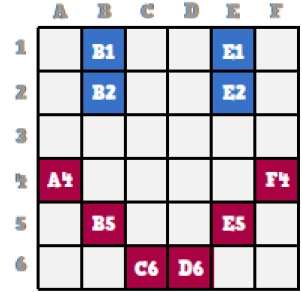
Orijinal gülen yüze yakından bakıldığında yukarıdaki şekilde B1, B2 ve E1, E2 olarak temsil edilen iki mavi çizgi olduğunu görebiliriz.

Aynı şekilde, gülen yüz, sırasıyla A4, B5, C6, D6, E5 ve F4'ün kombinasyon bitleri kullanılarak temsil edilir.

Bitmap grafiklerin ana dezavantajları şunlardır:

• Bitmap görüntüsünü yeniden boyutlandıramıyoruz. Yeniden boyutlandırmaya çalışırsanız pikseller bulanıklaşır.

• Renkli bit eşlemler çok büyük olabilir.

Dönüşüm, bazı grafikleri kurallar uygulayarak başka bir şeye dönüştürmek anlamına gelir. Çevirme, büyütme veya küçültme, döndürme, yamultma, vb. Gibi çeşitli dönüştürme türlerine sahip olabiliriz. Bir 2D düzlemde bir dönüşüm gerçekleştiğinde, buna 2D dönüştürme denir.

Dönüşümler, ekrandaki grafikleri yeniden konumlandırmak ve boyutlarını veya yönlerini değiştirmek için bilgisayar grafiklerinde önemli bir rol oynar.

Homojen Koordinatlar

Çevirme ve ardından döndürme ve ölçekleme gibi bir dönüşüm dizisi gerçekleştirmek için, sıralı bir süreci izlememiz gerekir -

• Koordinatları çevirin,
• Çevrilen koordinatları döndürün ve ardından
• Bileşik dönüştürmeyi tamamlamak için döndürülen koordinatları ölçekleyin.

Bu süreci kısaltmak için 2 × 2 dönüşüm matrisi yerine 3 × 3 dönüşüm matrisi kullanmalıyız. 2 × 2 bir matrisi 3 × 3 matrise dönüştürmek için fazladan bir kukla koordinat W eklemeliyiz.

Bu şekilde noktayı 2 sayı yerine 3 sayı ile temsil edebiliriz ki buna Homogenous Coordinatesistemi. Bu sistemde tüm dönüşüm denklemlerini matris çarpımında temsil edebiliriz. Herhangi bir Kartezyen noktası P (X, Y), P '(X _h , Y _h , h) ile homojen koordinatlara dönüştürülebilir .

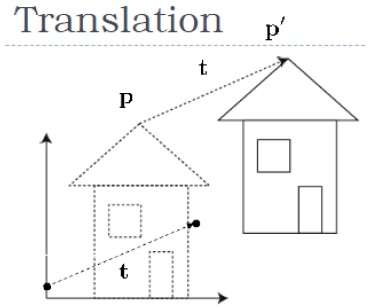
Tercüme

Çeviri, bir nesneyi ekranda farklı bir konuma taşır. Yeni koordinatı (X ', Y') elde etmek için orijinal koordinata (X, Y) çeviri koordinatını (t _x , t _y ) ekleyerek bir noktayı 2D olarak çevirebilirsiniz .

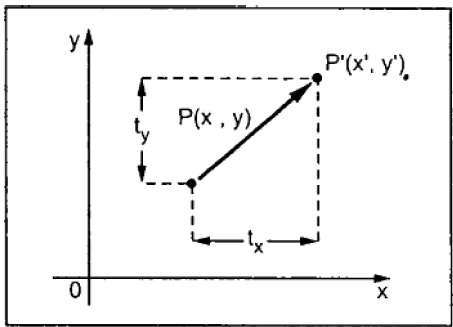
Yukarıdaki şekilden şunu yazabilirsiniz -

X’ = X + t_x

Y’ = Y + t_y

Çift (t _x , t _y ), çeviri vektörü veya kaydırma vektörü olarak adlandırılır. Yukarıdaki denklemler, sütun vektörleri kullanılarak da gösterilebilir.

$P = \frac{[X]}{[Y]}$ p '= $\frac{[X']}{[Y']}$T = $\frac{[t_{x}]}{[t_{y}]}$

Bunu şu şekilde yazabiliriz -

P’ = P + T

Rotasyon

Dönüşte, nesneyi başlangıç ​​noktasından belirli bir θ (teta) açısıyla döndürürüz. Aşağıdaki şekilden, P (X, Y) noktasının, orijinden r mesafesi ile yatay X koordinatından φ açısında bulunduğunu görebiliriz.

Θ açısında döndürmek istediğinizi varsayalım. Yeni bir konuma döndürdükten sonra, yeni bir P '(X', Y ') noktası alacaksınız.

Standart trigonometrik kullanılarak P (X, Y) noktasının orijinal koordinatı şu şekilde temsil edilebilir:

$X = r \, cos \, \phi ...... (1)$

$Y = r \, sin \, \phi ...... (2)$

Aynı şekilde P '(X', Y ') noktasını -

${x}'= r \: cos \: \left ( \phi \: + \: \theta \right ) = r\: cos \: \phi \: cos \: \theta \: − \: r \: sin \: \phi \: sin \: \theta ....... (3)$

${y}'= r \: sin \: \left ( \phi \: + \: \theta \right ) = r\: cos \: \phi \: sin \: \theta \: + \: r \: sin \: \phi \: cos \: \theta ....... (4)$

Sırasıyla (3) ve (4) 'te (1) ve (2) denklemini değiştirerek, alacağız

${x}'= x \: cos \: \theta − \: y \: sin \: \theta $

${y}'= x \: sin \: \theta + \: y \: cos \: \theta $

Yukarıdaki denklemi matris formunda temsil eden,

$$[X' Y'] = [X Y] \begin{bmatrix} cos\theta & sin\theta \\ −sin\theta & cos\theta \end{bmatrix}OR $$

P '= P ∙ R

R, rotasyon matrisidir

$$R = \begin{bmatrix} cos\theta & sin\theta \\ −sin\theta & cos\theta \end{bmatrix}$$

Dönüş açısı pozitif ve negatif olabilir.

Pozitif dönüş açısı için yukarıdaki rotasyon matrisini kullanabiliriz. Bununla birlikte, negatif açı dönüşü için, matris aşağıda gösterildiği gibi değişecektir -

$$R = \begin{bmatrix} cos(−\theta) & sin(−\theta) \\ -sin(−\theta) & cos(−\theta) \end{bmatrix}$$

$$=\begin{bmatrix} cos\theta & −sin\theta \\ sin\theta & cos\theta \end{bmatrix} \left (\because cos(−\theta ) = cos \theta \; and\; sin(−\theta ) = −sin \theta \right )$$

Ölçeklendirme

Bir nesnenin boyutunu değiştirmek için ölçeklendirme dönüşümü kullanılır. Ölçekleme sürecinde, nesnenin boyutlarını genişletir veya sıkıştırırsınız. Ölçekleme, istenen sonucu elde etmek için nesnenin orijinal koordinatlarını ölçekleme faktörüyle çarparak gerçekleştirilebilir.

Orijinal koordinatların (X, Y), ölçekleme faktörlerinin (S _X , S _Y ) ve üretilen koordinatların (X ', Y') olduğunu varsayalım . Bu, aşağıda gösterildiği gibi matematiksel olarak temsil edilebilir -

X' = X . S_X and Y' = Y . S_Y

Ölçekleme faktörü S _X , S _Y , nesneyi sırasıyla X ve Y yönünde ölçeklendirir. Yukarıdaki denklemler aşağıdaki gibi matris formunda da gösterilebilir -

$$\binom{X'}{Y'} = \binom{X}{Y} \begin{bmatrix} S_{x} & 0\\ 0 & S_{y} \end{bmatrix}$$

VEYA

P’ = P . S

S ölçekleme matrisidir. Ölçekleme işlemi aşağıdaki şekilde gösterilmektedir.

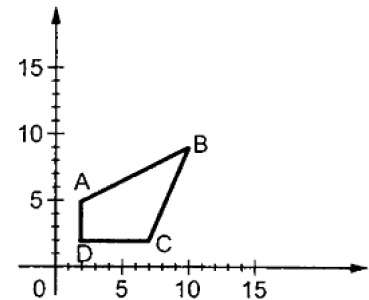
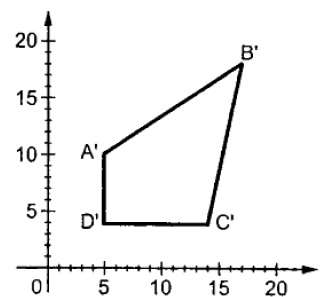
S ölçekleme faktörüne 1'den küçük değerler verirsek, nesnenin boyutunu küçültebiliriz. 1'den büyük değerler sağlarsak, nesnenin boyutunu artırabiliriz.

Yansıma

Yansıma, orijinal nesnenin ayna görüntüsüdür. Yani 180 ° 'lik bir rotasyon işlemi olduğunu söyleyebiliriz. Yansıma dönüşümünde nesnenin boyutu değişmez.

Aşağıdaki şekiller, sırasıyla X ve Y eksenlerine göre ve orijine ilişkin yansımaları göstermektedir.

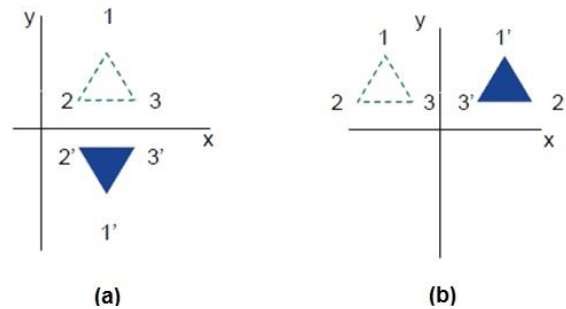
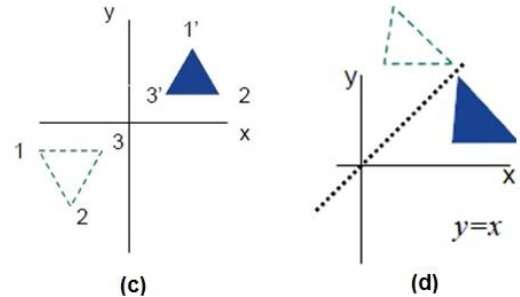
Kesme

Bir nesnenin şeklini eğimli hale getiren dönüşüme kesme dönüşümü denir. İki kayma dönüşümü vardırX-Shear ve Y-Shear. Biri X koordinat değerlerini, diğeri ise Y koordinat değerlerini kaydırır. Ancak; her iki durumda da sadece bir koordinat koordinatlarını değiştirir ve diğeri değerlerini korur. Kesme ayrıca şu şekilde adlandırılır:Skewing.

X-Shear

X-Shear, Y koordinatını korur ve X koordinatlarında değişiklikler yapılır, bu da dikey çizgilerin aşağıdaki şekilde gösterildiği gibi sağa veya sola eğilmesine neden olur.

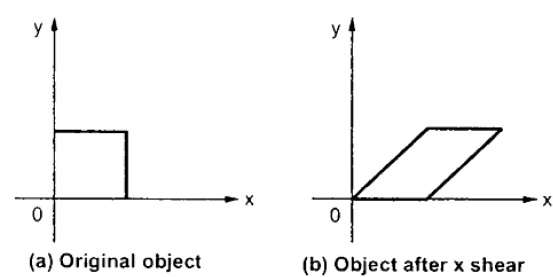
X-Shear için dönüşüm matrisi şu şekilde temsil edilebilir:

$$X_{sh} = \begin{bmatrix} 1& shx& 0\\ 0& 1& 0\\ 0& 0& 1 \end{bmatrix}$$

Y '= Y + Sh _y . X

X '= X

Y Kesme

Y Kayması, X koordinatlarını korur ve Y koordinatlarını değiştirerek yatay çizgilerin aşağıdaki şekilde gösterildiği gibi yukarı veya aşağı eğimli çizgilere dönüşmesine neden olur.

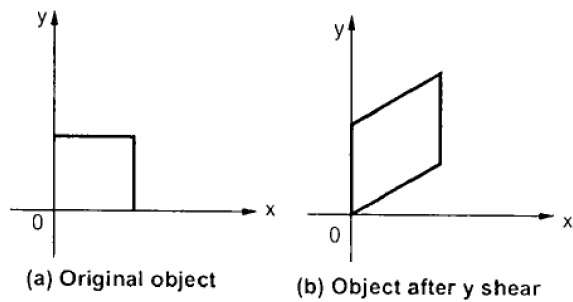
Y-Shear aşağıdaki gibi matriste gösterilebilir:

$$Y_{sh} \begin{bmatrix} 1& 0& 0\\ shy& 1& 0\\ 0& 0& 1 \end{bmatrix}$$

X '= X + Sh _x . Y

Y '= Y

Kompozit Dönüşüm

T1 düzleminin bir dönüşümünü ikinci bir düzlem dönüşümü T2 takip ediyorsa, o zaman sonucun kendisi, bu sırayla alınan T1 ve T2'nin bileşimi olan tek bir dönüşüm T ile temsil edilebilir. Bu, T = T1 ∙ T2 olarak yazılır.

Birleşik dönüşüm, birleşik bir dönüşüm matrisi elde etmek için dönüşüm matrislerinin birleştirilmesiyle elde edilebilir.

Birleşik bir matris -

[T][X] = [X] [T1] [T2] [T3] [T4] …. [Tn]

[Ti] şunun herhangi bir kombinasyonu

• Translation
• Scaling
• Shearing
• Rotation
• Reflection

Dönüşüm sırasındaki değişiklik, genel matris çarpımının kümülatif olmadığı, yani [A] olduğu için farklı sonuçlara yol açacaktır. [B] ≠ [B]. [A] ve çarpma sırası. Dönüşümleri oluşturmanın temel amacı, bir dizi dönüşümü birbiri ardına uygulamak yerine, tek bir bileşik dönüşümü bir noktaya uygulayarak verimlilik elde etmektir.

Örneğin, bir nesneyi gelişigüzel bir nokta (X _p , Y _p ) etrafında döndürmek için üç adım gerçekleştirmeliyiz -

• Noktayı (X _p , Y _p ) orijine çevirin.
• Başlangıç ​​noktası etrafında döndürün.
• Son olarak, dönme merkezini ait olduğu yere geri çevirin.

2D sistemde, yalnızca iki koordinat X ve Y kullanıyoruz, ancak 3D'de fazladan bir Z koordinatı ekleniyor. 3D grafik teknikleri ve uygulamaları eğlence, oyun ve bilgisayar destekli tasarım endüstrileri için temeldir. Bilimsel görselleştirmede devam eden bir araştırma alanıdır.

Ayrıca, 3B grafik bileşenleri artık hemen hemen her kişisel bilgisayarın bir parçasıdır ve geleneksel olarak oyunlar gibi grafik yoğun yazılımlar için tasarlansa da, diğer uygulamalar tarafından giderek daha fazla kullanılmaktadır.

Paralel Projeksiyon

Paralel projeksiyon, z koordinatını atar ve nesne üzerindeki her bir tepe noktasından gelen paralel çizgiler, görünüm düzlemiyle kesişene kadar uzatılır. Paralel projeksiyonda, projeksiyon merkezi yerine bir projeksiyon yönü belirleriz.

Paralel projeksiyonda, projeksiyon merkezinden yansıtma düzlemine olan mesafe sonsuzdur. Bu tür projeksiyonda, yansıtılan köşeleri orijinal nesne üzerindeki bağlantılara karşılık gelen çizgi segmentleriyle birleştiririz.

Paralel projeksiyonlar daha az gerçekçidir, ancak kesin ölçümler için iyidirler. Bu tür projeksiyonlarda paralel çizgiler paralel kalır ve açılar korunmaz. Aşağıdaki hiyerarşide çeşitli paralel projeksiyon türleri gösterilmektedir.

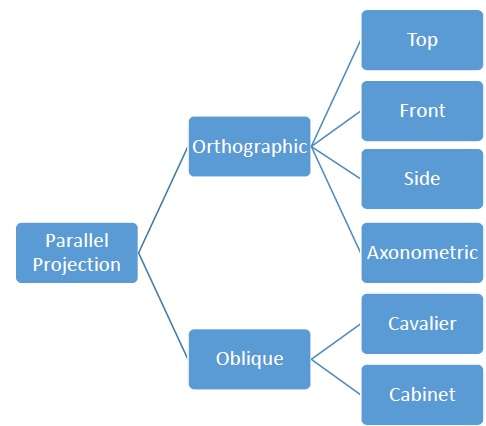
Ortografik projeksiyon

Ortografik izdüşümde, izdüşüm yönü düzlemin izdüşümüne normaldir. Üç tür ortografik izdüşüm vardır -

• Ön Projeksiyon
• En İyi Projeksiyon
• Yan Projeksiyon

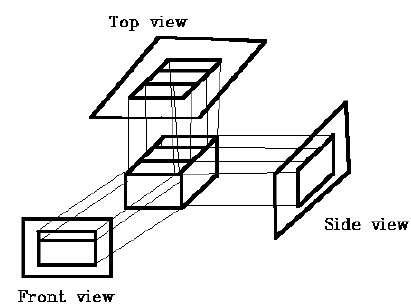
Eğik Projeksiyon

Eğik projeksiyonda, projeksiyonun yönü düzlemin izdüşümüne normal değildir. Eğik projeksiyonda, nesneyi ortografik izdüşümden daha iyi görebiliriz.

İki tür eğik çıkıntı vardır - Cavalier ve Cabinet. Cavalier projeksiyonu, projeksiyon düzlemi ile 45 ° açı yapar. Görüş düzlemine dik bir çizginin izdüşümü, Cavalier projeksiyonundaki çizginin kendisiyle aynı uzunluğa sahiptir. Bir şövalye projeksiyonunda, üç ana yönün tümü için kısaltma faktörleri eşittir.

Kabin projeksiyonu, projeksiyon düzlemi ile 63.4 ° açı yapar. Kabin projeksiyonunda, izleme yüzeyine dik olan çizgiler gerçek uzunluklarında ½ yansıtılır. Her iki çıkıntı aşağıdaki şekilde gösterilmektedir -

İzometrik Projeksiyonlar

Bir nesnenin birden fazla tarafını gösteren ortografik izdüşümler denir axonometric orthographic projections. En yaygın aksonometrik izdüşüm,isometric projectionprojeksiyon düzleminin model koordinat sistemindeki her bir koordinat eksenini eşit bir mesafede kesiştiği yer. Bu izdüşümde doğruların paralelliği korunur ancak açılar korunmaz. Aşağıdaki şekil izometrik projeksiyonu göstermektedir -

Perspektif Projeksiyon

Perspektif projeksiyonda, projeksiyonun merkezinden proje düzlemine olan mesafe sonludur ve nesnenin boyutu, daha gerçekçi görünen mesafe ile ters orantılı olarak değişir.

Mesafe ve açılar korunmaz ve paralel çizgiler paralel kalmaz. Bunun yerine, hepsi tek bir noktada birleşirler.center of projection veya projection reference point. Aşağıdaki çizelgede gösterilen 3 tür perspektif projeksiyonu vardır.

• One point perspektif izdüşümünün çizilmesi basittir.

• Two point perspektif projeksiyon daha iyi derinlik izlenimi verir.

• Three point perspektif izdüşümü çizmek en zordur.

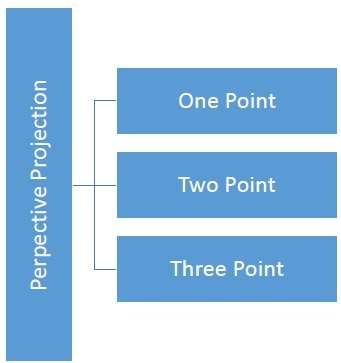
Aşağıdaki şekil, üç tür perspektif izdüşümünü göstermektedir -

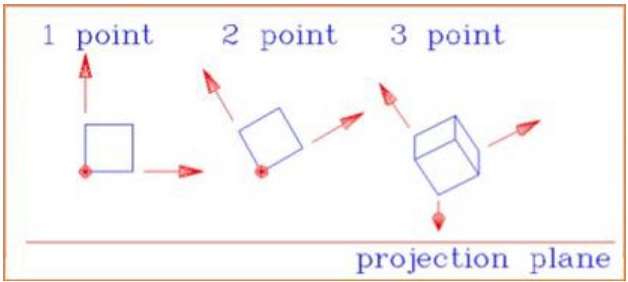
Tercüme

3D çeviride, Z koordinatını X ve Y koordinatlarıyla birlikte aktarıyoruz. 3D çeviri süreci, 2D çeviriye benzer. Çeviri, bir nesneyi ekranda farklı bir konuma taşır.

Aşağıdaki şekil, çevirinin etkisini göstermektedir -

Çeviri koordinatı eklenerek bir nokta 3B'ye çevrilebilir $(t_{x,} t_{y,} t_{z})$ yeni koordinatı (X ', Y', Z ') almak için orijinal koordinata (X, Y, Z).

$T = \begin{bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ t_{x}& t_{y}& t_{z}& 1\\ \end{bmatrix}$

P '= P ∙ T

$[X′ \:\: Y′ \:\: Z′ \:\: 1] \: = \: [X \:\: Y \:\: Z \:\: 1] \: \begin{bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ t_{x}& t_{y}& t_{z}& 1\\ \end{bmatrix}$

$= [X + t_{x} \:\:\: Y + t_{y} \:\:\: Z + t_{z} \:\:\: 1]$

Rotasyon

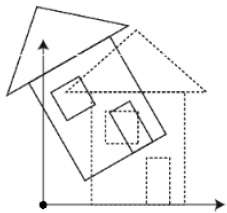
3B döndürme, 2B döndürme ile aynı değildir. 3B döndürmede, dönme açısını döndürme ekseni ile birlikte belirlememiz gerekir. X, Y ve Z eksenleri etrafında 3 boyutlu döndürme yapabiliriz. Aşağıdaki gibi matris biçiminde temsil edilirler -

$$R_{x}(\theta) = \begin{bmatrix} 1& 0& 0& 0\\ 0& cos\theta & −sin\theta& 0\\ 0& sin\theta & cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix} R_{y}(\theta) = \begin{bmatrix} cos\theta& 0& sin\theta& 0\\ 0& 1& 0& 0\\ −sin\theta& 0& cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix} R_{z}(\theta) =\begin{bmatrix} cos\theta & −sin\theta & 0& 0\\ sin\theta & cos\theta & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1 \end{bmatrix}$$

Aşağıdaki şekil, çeşitli eksenler etrafındaki dönüşü açıklamaktadır -

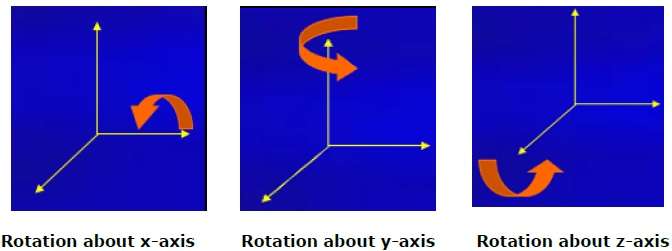
Ölçeklendirme

Ölçekleme dönüştürmesini kullanarak bir nesnenin boyutunu değiştirebilirsiniz. Ölçekleme sürecinde, nesnenin boyutlarını genişletir veya sıkıştırırsınız. Ölçekleme, istenen sonucu elde etmek için nesnenin orijinal koordinatlarını ölçekleme faktörüyle çarparak gerçekleştirilebilir. Aşağıdaki şekil, 3D ölçeklemenin etkisini göstermektedir -

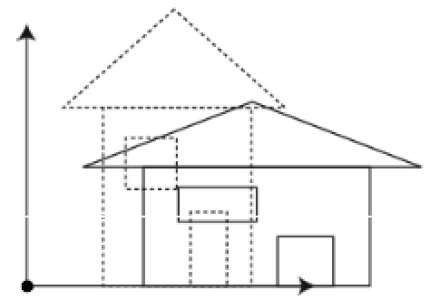
3D ölçekleme işleminde üç koordinat kullanılır. Orijinal koordinatların (X, Y, Z) olduğunu, ölçekleme faktörlerinin olduğunu varsayalım$(S_{X,} S_{Y,} S_{z})$sırasıyla ve üretilen koordinatlar (X ', Y', Z '). Bu, aşağıda gösterildiği gibi matematiksel olarak temsil edilebilir -

$S = \begin{bmatrix} S_{x}& 0& 0& 0\\ 0& S_{y}& 0& 0\\ 0& 0& S_{z}& 0\\ 0& 0& 0& 1 \end{bmatrix}$

P '= P ∙ S

$[{X}' \:\:\: {Y}' \:\:\: {Z}' \:\:\: 1] = [X \:\:\:Y \:\:\: Z \:\:\: 1] \:\: \begin{bmatrix} S_{x}& 0& 0& 0\\ 0& S_{y}& 0& 0\\ 0& 0& S_{z}& 0\\ 0& 0& 0& 1 \end{bmatrix}$

$ = [X.S_{x} \:\:\: Y.S_{y} \:\:\: Z.S_{z} \:\:\: 1]$

Kesme

Bir nesnenin şeklini eğimli bir dönüşüme denir. shear transformation. 2B yamultmada olduğu gibi, bir nesneyi 3B'de X ekseni, Y ekseni veya Z ekseni boyunca yamultabiliriz.

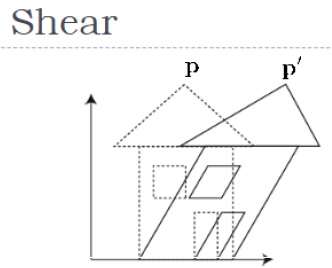
Yukarıdaki şekilde gösterildiği gibi, bir P koordinatı vardır, aşağıdaki gibi 3B matris formunda gösterilebilen yeni bir P 'koordinatını elde etmek için onu kesebilirsiniz -

$Sh = \begin{bmatrix} 1 & sh_{x}^{y} & sh_{x}^{z} & 0 \\ sh_{y}^{x} & 1 & sh_{y}^{z} & 0 \\ sh_{z}^{x} & sh_{z}^{y} & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$

P '= P ∙ Sh

$X’ = X + Sh_{x}^{y} Y + Sh_{x}^{z} Z$

$Y' = Sh_{y}^{x}X + Y +sh_{y}^{z}Z$

$Z' = Sh_{z}^{x}X + Sh_{z}^{y}Y + Z$

Dönüşüm Matrisleri

Dönüşüm matrisi, dönüşüm için temel bir araçtır. Nxm boyutlarına sahip bir matris, nesnelerin koordinatları ile çarpılır. Dönüşüm için genellikle 3 x 3 veya 4 x 4 matris kullanılır. Örneğin, çeşitli işlemler için aşağıdaki matrisi düşünün.

$T = \begin{bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ t_{x}& t_{y}& t_{z}& 1\\ \end{bmatrix}$	$S = \begin{bmatrix} S_{x}& 0& 0& 0\\ 0& S_{y}& 0& 0\\ 0& 0& S_{z}& 0\\ 0& 0& 0& 1 \end{bmatrix}$	$Sh = \begin{bmatrix} 1& sh_{x}^{y}& sh_{x}^{z}& 0\\ sh_{y}^{x}& 1 & sh_{y}^{z}& 0\\ sh_{z}^{x}& sh_{z}^{y}& 1& 0\\ 0& 0& 0& 1 \end{bmatrix}$
Translation Matrix	Scaling Matrix	Shear Matrix
$R_{x}(\theta) = \begin{bmatrix} 1& 0& 0& 0\\ 0& cos\theta & -sin\theta& 0\\ 0& sin\theta & cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix}$	$R_{y}(\theta) = \begin{bmatrix} cos\theta& 0& sin\theta& 0\\ 0& 1& 0& 0\\ -sin\theta& 0& cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix}$	$R_{z}(\theta) = \begin{bmatrix} cos\theta & -sin\theta & 0& 0\\ sin\theta & cos\theta & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1 \end{bmatrix}$
Rotation Matrix

Bilgisayar grafiklerinde, genellikle ekrana farklı türde nesneler çizmemiz gerekir. Nesneler her zaman düz değildir ve bir nesneyi çizmek için birçok kez eğri çizmemiz gerekir.

Eğri Türleri

Bir eğri, sonsuz büyüklükte bir nokta kümesidir. Uç noktalar dışında her noktanın iki komşusu vardır. Eğriler genel olarak üç kategoriye ayrılabilir -explicit, implicit, ve parametric curves.

Örtük Eğriler

Örtülü eğri temsilleri, eğri üzerinde bir noktanın olup olmadığını görmek için test edebilen bir prosedür kullanarak bir eğri üzerindeki nokta kümesini tanımlar. Genellikle, örtük bir eğri, formun örtük bir işlevi ile tanımlanır -

f (x, y) = 0

Birden çok değerli eğrileri temsil edebilir (bir x değeri için birden çok y değeri). Yaygın bir örnek, örtük temsili olan çemberdir.

x² + y² - R² = 0

Açık Eğriler

Bir matematiksel fonksiyon y = f (x) bir eğri olarak çizilebilir. Böyle bir fonksiyon, eğrinin açık temsilidir. Açık gösterim genel değildir çünkü dikey çizgileri temsil edemez ve ayrıca tek değerlidir. Her x değeri için, normalde işlev tarafından yalnızca tek bir y değeri hesaplanır.

Parametrik Eğriler

Parametrik biçime sahip eğrilere parametrik eğriler denir. Açık ve örtük eğri gösterimleri yalnızca işlev bilindiğinde kullanılabilir. Pratikte parametrik eğriler kullanılır. İki boyutlu bir parametrik eğri aşağıdaki forma sahiptir -

P (t) = f (t), g (t) veya P (t) = x (t), y (t)

F ve g fonksiyonları, eğri üzerindeki herhangi bir noktanın (x, y) koordinatları haline gelir ve noktalar, t parametresi belirli bir aralık [a, b], normalde [0, 1] boyunca değiştirildiğinde elde edilir.

Bezier Eğrileri

Bezier eğrisi Fransız mühendis tarafından keşfedildi Pierre Bézier. Bu eğriler, diğer noktaların kontrolü altında oluşturulabilir. Eğri oluşturmak için kontrol noktaları kullanılarak yaklaşık teğetler kullanılır. Bezier eğrisi matematiksel olarak şu şekilde gösterilebilir:

$$\sum_{k=0}^{n} P_{i}{B_{i}^{n}}(t)$$

Nerede $p_{i}$ puan kümesidir ve ${B_{i}^{n}}(t)$ - ile verilen Bernstein polinomlarını temsil eder -

$${B_{i}^{n}}(t) = \binom{n}{i} (1 - t)^{n-i}t^{i}$$

Nerede n polinom derecesi, i endeks ve t değişkendir.

En basit Bézier eğrisi, noktadan itibaren düz çizgidir $P_{0}$ -e $P_{1}$. İkinci dereceden bir Bezier eğrisi, üç kontrol noktası ile belirlenir. Kübik Bezier eğrisi, dört kontrol noktası tarafından belirlenir.

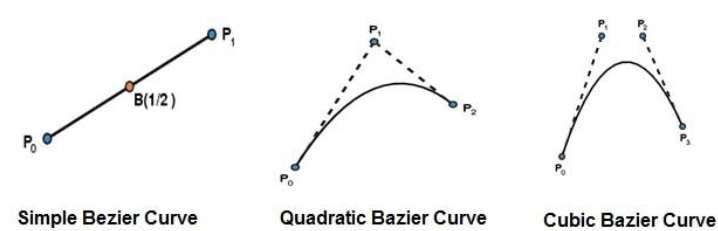
Bezier Eğrilerinin Özellikleri

Bezier eğrileri aşağıdaki özelliklere sahiptir -

• Genellikle, kontrol noktalarını birleştiren segmentlerden oluşan kontrol poligonunun şeklini takip ederler.

• Her zaman ilk ve son kontrol noktalarından geçerler.

• Tanımlayıcı kontrol noktalarının dışbükey gövdesinde bulunurlar.

• Eğri parçasını tanımlayan polinomun derecesi, tanımlayan çokgen noktasının sayısından bir eksiktir. Bu nedenle, 4 kontrol noktası için, polinomun derecesi 3'tür, yani kübik polinomdur.

• Bir Bezier eğrisi genellikle tanımlayıcı çokgenin şeklini takip eder.

• Uç noktalardaki teğet vektörün yönü, ilk ve son bölümler tarafından belirlenen vektörün yönü ile aynıdır.

• Bezier eğrisinin dışbükey gövde özelliği, polinomun kontrol noktalarını sorunsuz bir şekilde takip etmesini sağlar.

• Hiçbir düz çizgi, bir Bezier eğrisiyle, kontrol çokgeniyle kesiştiğinden daha fazla kesişmez.

• Afin bir dönüşüm altında değişmezler.

• Bezier eğrileri küresel kontrol gösterir, bir kontrol noktasını hareket ettirmek tüm eğrinin şeklini değiştirir.

• Belirli bir Bezier eğrisi, t = t0 noktasında t = t0 parametre değerine karşılık gelen noktada birleşen iki Bezier segmentine bölünebilir.

B-Spline Eğrileri

Bernstein temel işlevi tarafından üretilen Bezier eğrisi sınırlı esnekliğe sahiptir.

• İlk olarak, belirtilen çokgen köşelerinin sayısı, eğriyi tanımlayan sonuçta elde edilen polinomun sırasını sabitler.

• İkinci sınırlayıcı özellik, harmanlama fonksiyonunun değerinin, tüm eğri boyunca tüm parametre değerleri için sıfır olmamasıdır.

B-spline temeli, özel durum olarak Bernstein temelini içerir. B-spline temeli global değildir.

Bir B-spline eğrisi, kontrol noktaları Pi ve B-spline temel fonksiyonunun doğrusal bir kombinasyonu olarak tanımlanır $N_{i,}$ k (t) tarafından verilen

$C(t) = \sum_{i=0}^{n}P_{i}N_{i,k}(t),$ $n\geq k-1,$ $t\: \epsilon \: [ tk-1,tn+1 ]$

Nerede,

• {$p_{i}$: i = 0, 1, 2… .n} kontrol noktalarıdır

• k, B-spline eğrisinin polinom segmentlerinin sırasıdır. K sırası, eğrinin k - 1 dereceli parçalı polinom bölümlerinden oluştuğu anlamına gelir,

• $N_{i,k}(t)$"normalleştirilmiş B-spline karıştırma fonksiyonları" dır. Bunlar, k sırası ve normalde "düğüm dizisi" olarak adlandırılan azalan olmayan bir gerçek sayı dizisi ile tanımlanır.

$${t_{i}:i = 0, ... n + K}$$

N _i , k işlevleri aşağıdaki şekilde açıklanmıştır -

$$N_{i,1}(t) = \left\{\begin{matrix} 1,& if \:u \: \epsilon \: [t_{i,}t_{i+1}) \\ 0,& Otherwise \end{matrix}\right.$$

ve k> 1 ise,

$$N_{i,k}(t) = \frac{t-t_{i}}{t_{i+k-1}} N_{i,k-1}(t) + \frac{t_{i+k}-t}{t_{i+k} - t_{i+1}} N_{i+1,k-1}(t)$$

ve

$$t \: \epsilon \: [t_{k-1},t_{n+1})$$

B-spline Eğrisinin Özellikleri

B-spline eğrileri aşağıdaki özelliklere sahiptir -

• Herhangi bir parametre değeri için B-spline temel fonksiyonlarının toplamı 1'dir.

• Her temel fonksiyon, tüm parametre değerleri için pozitif veya sıfırdır.

• Her temel fonksiyonun k = 1 dışında tam olarak bir maksimum değeri vardır.

• Eğrinin maksimum sırası, çokgeni tanımlayan köşe sayısına eşittir.

• B-spline polinomunun derecesi, tanımlayan çokgenin köşe sayısından bağımsızdır.

• B-spline, eğri yüzeyi üzerinde yerel kontrole izin verir çünkü her köşe, bir eğrinin şeklini yalnızca ilişkili temel fonksiyonunun sıfır olmadığı bir dizi parametre değeri üzerinde etkiler.

• Eğri, varyasyonu azaltma özelliğini sergiler.

• Eğri genellikle tanımlayıcı çokgen şeklini takip eder.

• Herhangi bir afin dönüşüm, çokgeni tanımlayan köşelere uygulanarak eğriye uygulanabilir.

• Tanımlayıcı çokgeninin dışbükey gövdesi içindeki eğri çizgisi.

Poligon Yüzeyler

Nesneler bir yüzeyler koleksiyonu olarak temsil edilir. 3D nesne gösterimi iki kategoriye ayrılmıştır.

• Boundary Representations (B-reps) - Bir 3B nesneyi, nesnenin iç kısmını ortamdan ayıran bir dizi yüzey olarak tanımlar.

• Space–partitioning representations - Bir nesneyi içeren uzamsal bölgeyi bir dizi küçük, üst üste binmeyen, bitişik katılara (genellikle küpler) bölerek iç özellikleri tanımlamak için kullanılır.

Bir 3B grafik nesnesi için en yaygın kullanılan sınır temsili, nesnenin iç kısmını çevreleyen bir dizi yüzey poligonudur. Birçok grafik sistemi bu yöntemi kullanır. Nesne açıklaması için çokgen seti saklanır. Bu, tüm yüzeyler doğrusal denklemlerle tanımlanabildiğinden, yüzey işlemesini ve nesnenin görüntülenmesini basitleştirir ve hızlandırır.

Çokgen yüzeyler, tasarım ve katı modelleme uygulamalarında yaygındır, çünkü wireframe displayyüzey yapısı hakkında genel bir fikir vermek için hızlı bir şekilde yapılabilir. Ardından, aydınlatmak için çokgen yüzey boyunca gölgelendirme desenlerinin enterpolasyonuyla gerçekçi sahneler üretilir.

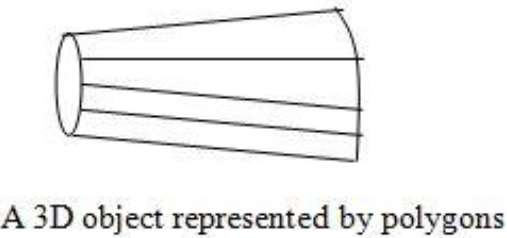
Poligon Tabloları

Bu yöntemde yüzey, köşe koordinatları ve ilişkili nitelikler kümesi tarafından belirlenir. Aşağıdaki şekilde gösterildiği gibi, v _1'den v _5'e kadar beş köşe vardır .

• Her köşe, tabloda v ₁ : x ₁ , y ₁ , z ₁ olarak temsil edilen x, y ve z koordinat bilgilerini depolar .

• Kenar tablosu, çokgenin kenar bilgilerini saklamak için kullanılır. Aşağıdaki şekilde, E ₁ kenarı , tabloda E ₁ : v ₁ , v ₂ olarak gösterilen köşe v ₁ ve v ₂ arasında yer alır .

• Poligon yüzey tablosu, poligonda bulunan yüzeylerin sayısını depolar. Aşağıdaki şekilden, S ₁ yüzeyi , çokgen yüzey tablosunda S ₁ olarak gösterilebilen E ₁ , E ₂ ve E ₃ kenarları ile kaplanmıştır : E ₁ , E ₂ ve E ₃ .

Düzlem Denklemleri

Düzlem yüzey denklemi şu şekilde ifade edilebilir:

Ax + By + Cz + D = 0

Burada (x, y, z) düzlemdeki herhangi bir noktadır ve A, B, C ve D katsayıları düzlemin uzamsal özelliklerini tanımlayan sabitlerdir. Düzlemdeki eşdoğrusal olmayan üç nokta için koordinat değerlerini kullanarak bir dizi üç düzlem denklemi çözerek A, B, C ve D değerlerini elde edebiliriz. Düzlemin üç köşesinin (x ₁ , y ₁ , z ₁ ), (x ₂ , y ₂ , z ₂ ) ve (x ₃ , y ₃ , z ₃ ) olduğunu varsayalım .

A / D, B / D ve C / D oranları için aşağıdaki eşzamanlı denklemleri çözelim. A, B, C ve D değerlerini alırsınız.

(A / D) x ₁ + (B / D) y ₁ + (C / D) z ₁ = -1

(A / D) x ₂ + (B / D) y ₂ + (C / D) z ₂ = -1

(A / D) x ₃ + (B / D) y ₃ + (C / D) z ₃ = -1

Yukarıdaki denklemleri determinant formda elde etmek için, Cramer kuralını yukarıdaki denklemlere uygulayın.

$A = \begin{bmatrix} 1& y_{1}& z_{1}\\ 1& y_{2}& z_{2}\\ 1& y_{3}& z_{3} \end{bmatrix} B = \begin{bmatrix} x_{1}& 1& z_{1}\\ x_{2}& 1& z_{2}\\ x_{3}& 1& z_{3} \end{bmatrix} C = \begin{bmatrix} x_{1}& y_{1}& 1\\ x_{2}& y_{2}& 1\\ x_{3}& y_{3}& 1 \end{bmatrix} D = - \begin{bmatrix} x_{1}& y_{1}& z_{1}\\ x_{2}& y_{2}& z_{2}\\ x_{3}& y_{3}& z_{3} \end{bmatrix}$

A, B, C ve D parametreli herhangi bir nokta (x, y, z) için şunu söyleyebiliriz -

• Ax + By + Cz + D ≠ 0, noktanın düzlemde olmadığı anlamına gelir.

• Ax + By + Cz + D <0, noktanın yüzeyin içinde olduğu anlamına gelir.

• Ax + By + Cz + D> 0, noktanın yüzeyin dışında olduğu anlamına gelir.

Poligon Kafesler

3B yüzeyler ve katılar, bir dizi çokgen ve çizgi elemanıyla yaklaşık olarak tahmin edilebilir. Bu tür yüzeyler denirpolygonal meshes. Çokgen ağda, her kenar en fazla iki çokgen tarafından paylaşılır. Çokgenler veya yüzler kümesi birlikte nesnenin "kaplamasını" oluşturur.

Bu yöntem, grafiklerde geniş bir katı / yüzey sınıfını temsil etmek için kullanılabilir. Gizli yüzey kaldırma algoritmaları kullanılarak çokgen bir ağ oluşturulabilir. Çokgen ağ, üç yolla temsil edilebilir -

• Açık temsil
• Köşe listesine işaretçiler
• Bir kenar listesine işaretçiler

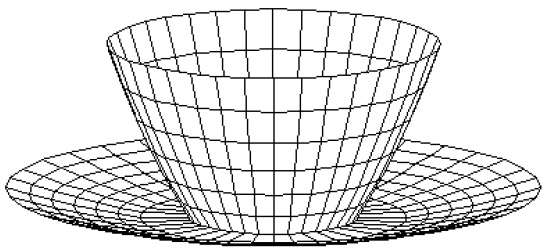
Avantajlar

• Hemen hemen her nesneyi modellemek için kullanılabilir.
• Bir köşe koleksiyonu olarak gösterilmeleri kolaydır.
• Dönüştürmeleri kolaydır.
• Bilgisayar ekranında çizmeleri kolaydır.

Dezavantajları

• Eğimli yüzeyler yalnızca yaklaşık olarak tanımlanabilir.
• Saç veya sıvı gibi bazı nesnelerin simülasyonunu yapmak zordur.

Saydam olmayan nesneler ve yüzeyler içeren bir resmi gördüğümüzde, göze yakın nesnelerin arkasında bulunan nesneleri görüşten göremeyiz. Gerçekçi bir ekran görüntüsü elde etmek için bu gizli yüzeyleri kaldırmalıyız. Bu yüzeylerin tanımlanmasına ve kaldırılmasına denirHidden-surface problem.

Gizli yüzey sorunlarını ortadan kaldırmak için iki yaklaşım vardır - Object-Space method ve Image-space method. Nesne-uzay yöntemi fiziksel koordinat sisteminde, görüntü-uzay yöntemi ise ekran koordinat sisteminde uygulanmaktadır.

Bir 2B ekranda bir 3B nesneyi görüntülemek istediğimizde, ekranın seçilen bir görüntüleme konumundan görülebilen kısımlarını tanımlamamız gerekir.

Derinlik Tamponu (Z-Tampon) Yöntemi

Bu yöntem Cutmull tarafından geliştirilmiştir. Bu bir görüntü-uzay yaklaşımıdır. Temel fikir, en yakın (görünür) yüzeyi belirlemek için her yüzeyin Z derinliğini test etmektir.

Bu yöntemde, her yüzey, yüzey boyunca bir seferde bir piksel konumunda ayrı ayrı işlenir. Bir piksel için derinlik değerleri karşılaştırılır ve en yakın (en küçük z) yüzey, çerçeve arabelleğinde görüntülenecek rengi belirler.

Poligon yüzeylerine çok verimli bir şekilde uygulanır. Yüzeyler herhangi bir sırayla işlenebilir. Uzaktaki poligonları geçersiz kılmak için iki tampon adıframe buffer ve depth buffer, kullanılmış.

Depth buffer yüzeyler işlenirken (0 ≤ derinlik ≤ 1) (x, y) konumu için derinlik değerlerini depolamak için kullanılır.

frame buffer her konumdaki (x, y) renk değerinin yoğunluk değerini saklamak için kullanılır.

Z koordinatları genellikle [0, 1] aralığına normalleştirilir. Z koordinatı için 0 değeri geri kırpma bölmesini belirtir ve z koordinatları için 1 değer ön kırpma bölmesini belirtir.

Algoritma

Step-1 - Tampon değerlerini ayarlayın -

Depthbuffer (x, y) = 0

Framebuffer (x, y) = arka plan rengi

Step-2 - Her çokgeni işleyin (Bir defada bir)

Bir çokgenin öngörülen her (x, y) piksel konumu için derinliği z hesaplayın.

Z> deepbuffer (x, y) ise

Yüzey rengini hesaplayın,

derinlik tamponunu (x, y) = z olarak ayarla,

framebuffer (x, y) = yüzey rengi (x, y)

Avantajlar

• Uygulaması kolaydır.
• Donanıma uygulanırsa hız problemini azaltır.
• Her seferinde bir nesneyi işler.

Dezavantajları

• Büyük hafıza gerektirir.
• Zaman alıcı bir süreçtir.

Tarama Satırı Yöntemi

Görünür yüzeyi tanımlamak için kullanılan bir görüntü-uzay yöntemidir. Bu yöntem, yalnızca tek tarama satırı için derinlik bilgisine sahiptir. Tek bir tarama satırı derinlik değerleri gerektirmek için, bir sonraki tarama çizgisini işlemeden önce belirli bir tarama çizgisini aynı anda kesen tüm çokgenleri gruplamalı ve işlemeliyiz. İki önemli tablo,edge table ve polygon table, bunun için muhafaza edilmektedir.

The Edge Table - Sahnedeki her çizginin koordinat uç noktalarını, her çizginin ters eğimini ve kenarları yüzeylere bağlamak için poligon tablosundaki işaretçileri içerir.

The Polygon Table - Düzlem katsayılarını, yüzey malzemesi özelliklerini, diğer yüzey verilerini içerir ve kenar tablosuna işaret edebilir.

Belirli bir tarama çizgisini geçen yüzeylerin aranmasını kolaylaştırmak için, aktif bir kenar listesi oluşturulur. Aktif liste, yalnızca artan x sırasına göre tarama çizgisini geçen kenarları depolar. Ayrıca, bir tarama çizgisi boyunca bir konumun yüzeyin içinde mi yoksa dışında mı olduğunu belirtmek için her yüzey için bir bayrak yerleştirilir.

Her bir tarama çizgisindeki piksel konumları soldan sağa doğru işlenir. Yüzeyle sol kesişme noktasında yüzey bayrağı açılır ve sağda bayrak kapatılır. Yalnızca belirli bir tarama hattı konumunda birden çok yüzey bayrakları açıkken derinlik hesaplamaları yapmanız gerekir.

Alan-Alt Bölüm Yöntemi

Alan-altbölüm yöntemi, tek bir yüzeyin parçasını temsil eden bu görünüm alanlarını konumlandırarak avantaj sağlar. Toplam görüntüleme alanını, her küçük alan tek bir görünür yüzeyin bir kısmının izdüşümü oluncaya veya hiç yüzey olmayana kadar daha küçük dikdörtgenlere bölün.

Alt bölümler tek bir yüzeye ait olarak kolayca analiz edilene veya tek bir piksel boyutuna küçültülene kadar bu işleme devam edin. Bunu yapmanın kolay bir yolu, alanı her adımda art arda dört eşit parçaya bölmektir. Bir yüzeyin belirli bir alan sınırıyla sahip olabileceği dört olası ilişki vardır.

• Surrounding surface - Alanı tamamen çevreleyen bir tane.

• Overlapping surface - Kısmen alanın içinde ve kısmen dışında olan.

• Inside surface - Tamamen bölgenin içinde olan bir tane.

• Outside surface - Tamamen bölgenin dışında olan bir tane.

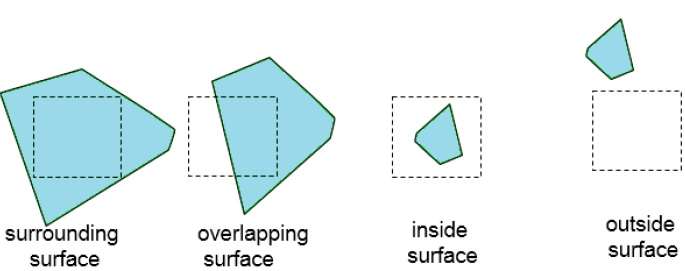
Bir alan içinde yüzey görünürlüğünü belirlemeye yönelik testler bu dört sınıflandırma açısından ifade edilebilir. Aşağıdaki koşullardan biri doğruysa, belirli bir alanın başka alt bölümlerine gerek yoktur -

• Tüm yüzeyler alana göre dış yüzeylerdir.
• Bölgede yalnızca bir iç, üst üste binen veya çevreleyen yüzey vardır.
• Çevreleyen bir yüzey, alan sınırları içindeki diğer tüm yüzeyleri gizler.

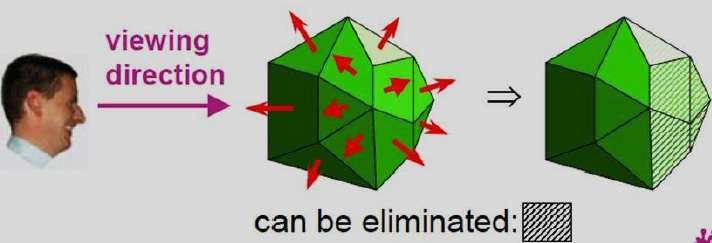
Arka Yüz Algılama

Bir çokyüzlünün arka yüzlerini tanımlamaya yönelik hızlı ve basit bir nesne-uzay yöntemi, "iç-dış" testlere dayanır. Bir nokta (x, y, z), eğer A, B, C ve D düzlem parametreleri olan bir poligon yüzeyinin "içindedir". Bir iç nokta yüzeyin görüş hattı boyunca olduğunda, çokgen bir arka yüz olmalıdır o yüzün içindeyiz ve önünü bizim bakış açımızdan göremiyoruz).

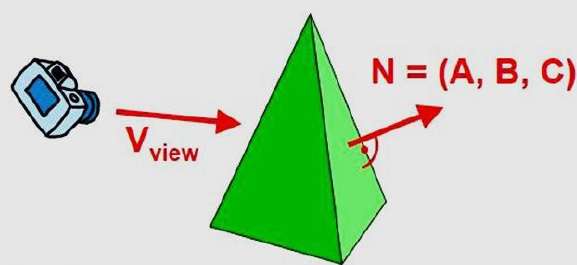
Normal vektörü dikkate alarak bu testi basitleştirebiliriz N Kartezyen bileşenlere (A, B, C) sahip çokgen bir yüzeye.

Genel olarak, V, göz (veya "kamera") konumundan görüntüleme yönünde bir vektörse, bu çokgen bir arka yüzdür.

V.N > 0

Ayrıca, nesne açıklamaları projeksiyon koordinatlarına dönüştürülürse ve görüntüleme yönünüz görüntüleme z eksenine paralelse, o zaman -

V = (0, 0, V _z ) ve V.N = V _Z C

Böylece sadece C'nin işaretini normal vektörün bileşeni olarak düşünmemiz gerekir. N.

Negatif yön boyunca bakış yönü olan sağ elini kullanan bir görüntüleme sisteminde $Z_{V}$eksen, C <0 ise çokgen bir arka yüzdür. Ayrıca, normal z bileşeni C = 0 olan herhangi bir yüzü göremeyiz, çünkü sizin bakış yönünüz o çokgene doğrudur. Bu nedenle, genel olarak herhangi bir poligonu, normal vektörü az bileşen değerine sahipse arka yüz olarak etiketleyebiliriz -

C <= 0

Solak görüntüleme sistemi kullanan paketlerde de benzer yöntemler kullanılabilir. Bu paketlerde, A, B, C ve D düzlem parametreleri, saat yönünde belirtilen çokgen köşe koordinatlarından hesaplanabilir (sağ elini kullanan bir sistemde kullanılan saatin tersi yönünün aksine).

Ayrıca, arka yüzler, görüntüleme konumundan uzaklaşan normal vektörlere sahiptir ve görüş yönü pozitif boyunca olduğunda C> = 0 ile tanımlanır. $Z_{v}$eksen. Bir nesneyi tanımlayan farklı düzlemler için C parametresini inceleyerek, tüm arka yüzleri anında belirleyebiliriz.

A-Buffer Yöntemi

A-arabellek yöntemi, derinlik-arabelleği yönteminin bir uzantısıdır. A-arabellek yöntemi, Lucas Film Stüdyolarında, Gördüğünüz Her Şeyi Renders You Ever (REYES) işleme sistemi için geliştirilmiş bir görünürlük algılama yöntemidir.

A-arabellek, asetatlara izin vermek için derinlik arabelleği yöntemini genişletir. A-tamponundaki anahtar veri yapısı biriktirme tamponudur.

A-arabellekteki her pozisyonun iki alanı vardır -

• Depth field - Pozitif veya negatif bir gerçek sayı depolar

• Intensity field - Yüzey yoğunluğu bilgilerini veya bir işaretçi değerini depolar

Derinlik> = 0 ise, bu konumda depolanan sayı, karşılık gelen piksel alanıyla örtüşen tek bir yüzeyin derinliğidir. Yoğunluk alanı daha sonra bu noktada yüzey renginin RGB bileşenlerini ve piksel kapsama yüzdesini depolar.

Derinlik <0 ise, piksel yoğunluğuna çoklu yüzey katkılarını gösterir. Yoğunluk alanı daha sonra bağlantılı bir yüzey verileri listesine bir işaretçi depolar. A tamponundaki yüzey tamponu şunları içerir:

• RGB yoğunluk bileşenleri
• Opaklık Parametresi
• Depth
• Alan kapsama yüzdesi
• Yüzey tanımlayıcı

Algoritma, derinlik tampon algoritması gibi ilerler. Derinlik ve opaklık değerleri, bir pikselin son rengini belirlemek için kullanılır.

Derinlik Sıralama Yöntemi

Derinlik sıralama yöntemi hem görüntü alanı hem de nesne alanı işlemlerini kullanır. Derinlemesine sıralama yöntemi iki temel işlevi yerine getirir -

• Önce yüzeyler azalan derinliğe göre sıralanır.

• İkincisi, yüzeyler, en derin yüzeyden başlayarak sırayla taranarak dönüştürülür.

Çokgen yüzeylerin tarama dönüşümü, görüntü uzayında gerçekleştirilir. Gizli yüzey problemini çözmek için kullanılan bu yöntem genelliklepainter's algorithm. Aşağıdaki şekil, derinlik sınıflandırmasının etkisini göstermektedir -

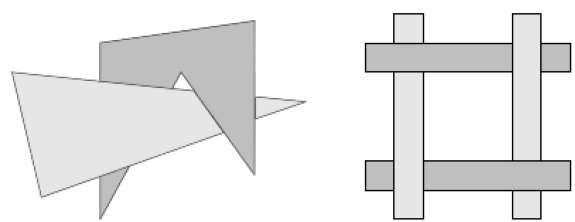
Algoritma, derinliğe göre sıralayarak başlar. Örneğin, bir çokgenin başlangıç ​​"derinlik" tahmini, çokgenin herhangi bir tepe noktasına en yakın z değeri olarak alınabilir.

Listenin sonundaki P poligonunu alalım. Z kapsamları P'lerle örtüşen tüm Q çokgenlerini düşünün. P'yi çizmeden önce aşağıdaki testleri yapıyoruz. Aşağıdaki testlerden herhangi biri pozitifse, P'nin Q'dan önce çizilebileceğini varsayabiliriz.

• X-uzantıları çakışmıyor mu?
• Y uzantıları çakışmıyor mu?
• P, bakış açısından Q'nun düzleminin tamamen zıt tarafında mı?
• Q, bakış açısı ile tamamen P'nin düzleminin aynı tarafında mı?
• Çokgenlerin izdüşümleri çakışmıyor mu?

Tüm testler başarısız olursa, diğerinin düzlemini kullanarak P veya Q'yu böleriz. Yeni kesilmiş çokgenler derinlik sırasına giriyor ve işlem devam ediyor. Teorik olarak, bu bölümleme O (n ² ) ayrı çokgen oluşturabilir, ancak pratikte çokgen sayısı çok daha azdır.

İkili Uzay Bölme (BSP) Ağaçları

Görünürlüğü hesaplamak için ikili alan bölümleme kullanılır. BSP ağaçlarını oluşturmak için çokgenlerle başlamalı ve tüm kenarları etiketlemelisiniz. Bir seferde yalnızca bir kenarı ele alarak, her kenarı, düzlemi ikiye bölecek şekilde uzatın. Ağacın ilk kenarını kök olarak yerleştirin. İçeride veya dışarıda olmalarına göre sonraki kenarları ekleyin. Zaten ağaçta bulunan bir kenarın uzantısına yayılan kenarlar ikiye bölünür ve her ikisi de ağaca eklenir.

• Yukarıdaki şekilden önce alın A bir kök olarak.

• Şekil (a) 'daki tüm düğümlerin bir listesini yapın.

• Kökün önüne gelen tüm düğümleri koyun A düğümün sol tarafına A ve kökün arkasındaki tüm bu düğümleri A Şekil (b) 'de gösterildiği gibi sağ tarafa.

• Önce tüm ön düğümleri, ardından arkadaki düğümleri işleyin.

• Şekil (c) 'de gösterildiği gibi, önce düğümü işleyeceğiz B. Düğümün önünde hiçbir şey olmadığı içinBNIL koyduk. Ancak, düğümümüz varC düğümün arkasında Byani düğüm C düğümün sağ tarafına gidecek B.

• Düğüm için aynı işlemi tekrarlayın D.

Bir Fransız / Amerikalı matematikçi Dr Benoit Mandelbrot Fraktalleri keşfetti. Fraktal kelimesi , kırık anlamına gelen Latince bir kelime olan fractus'tan türetilmiştir .

Fraktal nedir?

Fraktallar, bir bilgisayar tarafından tek bir formülle oluşturulan çok karmaşık resimlerdir. Yinelemeler kullanılarak oluşturulurlar. Bu, önceki yinelemenin sonuçları dikkate alınarak bir formülün biraz farklı değerlerle tekrar tekrar tekrarlandığı anlamına gelir.

Fraktallar aşağıdakiler gibi birçok alanda kullanılır:

• Astronomy - Galaksileri, Satürn halkalarını vb. Analiz etmek için.

• Biology/Chemistry - Bakteri kültürlerini, Kimyasal reaksiyonları, insan anatomisini, molekülleri, bitkileri tasvir etmek için,

• Others - Bulutları, kıyı şeridini ve sınır çizgilerini, veri sıkıştırma, yayılma, ekonomi, fraktal sanat, fraktal müzik, manzara, özel efekt vb.

Fraktalların Üretimi

Aşağıdaki şekilde gösterildiği gibi aynı şeklin tekrar tekrar tekrarlanmasıyla fraktallar oluşturulabilir. Şekil (a) bir eşkenar üçgeni göstermektedir. Şekil (b) 'de yıldız benzeri bir şekil oluşturmak için üçgenin tekrarlandığını görebiliriz. Şekil (c) 'de, şekil (b)' deki yıldız şeklinin yeni bir şekil oluşturmak için tekrar tekrar tekrarlandığını görebiliriz.

İstenilen bir şekli oluşturmak için sınırsız sayıda yineleme yapabiliriz. Programlama terimlerinde, bu tür şekilleri oluşturmak için özyineleme kullanılır.

Geometrik Fraktallar

Geometrik fraktallar, doğada bulunan, tam sayı olmayan veya fraktal boyutlara sahip şekillerle ilgilenir. Geometrik olarak deterministik (rastgele olmayan) kendine benzer bir fraktal oluşturmak için, belirli bir geometrik şekille başlıyoruz.initiator. Başlatıcı alt bölümleri daha sonra, adı verilen bir modelle değiştirilir.generator.

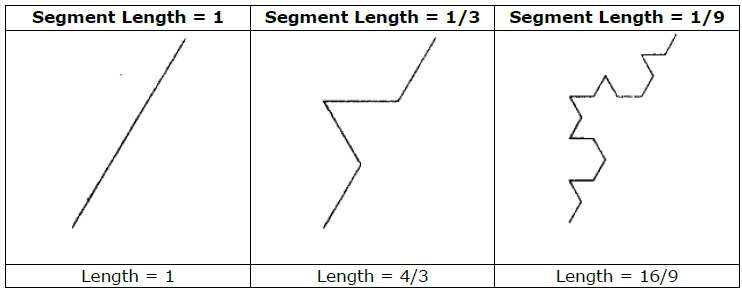
Örnek olarak, yukarıdaki şekilde gösterilen başlatıcı ve oluşturucuyu kullanırsak, onu tekrarlayarak iyi bir model oluşturabiliriz. Başlatıcıdaki her düz çizgi parçası, her adımda dört eşit uzunlukta çizgi parçasıyla değiştirilir. Ölçekleme faktörü 1 / 3'tür, dolayısıyla fraktal boyut D = ln 4 / ln 3 ≈ 1.2619'dur.

Ayrıca, başlatıcıdaki her çizgi parçasının uzunluğu her adımda 4/3 kat artar, böylece aşağıdaki şekilde gösterildiği gibi eğriye daha fazla ayrıntı eklendikçe fraktal eğrinin uzunluğu sonsuza meyleder -

Animasyon, bilgisayar grafiklerinde herhangi bir nesneye hayat vermek demektir. Cansız görünen nesnelere enerji ve duyguları enjekte etme gücüne sahiptir. Bilgisayar destekli animasyon ve bilgisayar tarafından oluşturulan animasyon, bilgisayar animasyonunun iki kategorisidir. Film veya video ile sunulabilir.

Animasyonun arkasındaki temel fikir, kaydedilen görüntüleri insan gözünü yanıltarak onları sürekli hareket olarak yorumlamaya yetecek hızlarda oynatmaktır. Animasyon, bir dizi ölü görüntünün canlanmasını sağlayabilir. Animasyon, eğlence, bilgisayar destekli tasarım, bilimsel görselleştirme, eğitim, eğitim, e-ticaret ve bilgisayar sanatı gibi birçok alanda kullanılabilir.

Animasyon Teknikleri

Animatörler, çeşitli farklı animasyon teknikleri icat etmiş ve kullanmıştır. Temel olarak bu bölümde tek tek tartışacağımız altı animasyon tekniği var.

Geleneksel Animasyon (kare kare)

Geleneksel olarak animasyonun çoğu elle yapıldı. Bir animasyondaki tüm karelerin elle çizilmesi gerekiyordu. Her bir animasyon saniyesi 24 kare (film) gerektirdiğinden, en kısa filmleri bile yaratmak için gereken çaba muazzam olabilir.

Keyframe oluşturma

Bu teknikte, bir hikaye panosu oluşturulur ve ardından sanatçılar animasyonun ana karelerini çizerler. Ana çerçeveler, belirgin değişikliklerin gerçekleştiği çerçevelerdir. Bunlar animasyonun kilit noktalarıdır. Anahtar çerçeve oluşturma, animatörün nesneler için kritik veya anahtar konumlar belirlemesini gerektirir. Bilgisayar daha sonra bu konumlar arasında sorunsuz bir şekilde enterpolasyon yaparak eksik kareleri otomatik olarak doldurur.

Prosedürel

Prosedürel bir animasyonda, nesnelere anahtar kare oluşturmayla değil, bir prosedürle (bir kurallar dizisi) canlandırılır. Animatör, kuralları ve başlangıç ​​koşullarını belirler ve simülasyonu çalıştırır. Kurallar genellikle matematiksel denklemlerle ifade edilen gerçek dünyanın fiziksel kurallarına dayanır.

Davranışsal

Davranışsal animasyonda, özerk bir karakter, en azından bir dereceye kadar kendi eylemlerini belirler. Bu, karaktere doğaçlama yapma yeteneği verir ve animatörü her karakterin hareketinin her ayrıntısını belirleme ihtiyacından kurtarır.

Performans Tabanlı (Hareket Yakalama)

Başka bir teknik de, manyetik veya görüş tabanlı sensörlerin bir insan veya hayvan nesnesinin hareketlerini üç boyutlu olarak kaydettiği Hareket Yakalama tekniğidir. Bir bilgisayar daha sonra nesneyi canlandırmak için bu verileri kullanır.

Bu teknoloji, bir dizi ünlü sporcunun spor video oyunlarındaki karakterler için eylemler sağlamasını sağlamıştır. Hareket yakalama animatörler arasında oldukça popülerdir çünkü bazı sıradan insan eylemleri nispeten kolaylıkla yakalanabilir. Bununla birlikte, konunun şekilleri veya boyutları ile grafiksel karakter arasında ciddi farklılıklar olabilir ve bu da tam uygulama sorunlarına yol açabilir.

Fiziksel Temelli (Dinamik)

Temel çerçeveleme ve sinema filmlerinden farklı olarak simülasyon, resimlerin ve diğer nesnelerin hareketini oluşturmak için fizik kanunlarını kullanır. Simülasyonlar, fiziksel gerçekçiliği korurken biraz farklı diziler üretmek için kolayca kullanılabilir. İkinci olarak, gerçek zamanlı simülasyonlar, gerçek kişinin simüle edilmiş karakterin eylemlerini yönetebildiği daha yüksek bir etkileşim derecesine izin verir.

Aksine, anahtar çerçeveleme ve hareket seçme ve değiştirme hareketlerine dayalı uygulamalar, önceden hesaplanmış bir hareket kitaplığı oluşturur. Simülasyonun uğradığı bir dezavantaj, uygun kontrol sistemlerini elle işlemek için gereken uzmanlık ve zamandır.

Anahtar Çerçeveleme

Anahtar kare, animasyondaki değişiklikleri tanımladığımız bir karedir. Her kare, kare kare animasyon oluşturduğumuzda bir anahtar karedir. Bir kişi bilgisayarda bir 3B animasyon oluşturduğunda, genellikle herhangi bir nesnenin her karede tam konumunu belirtmez. Anahtar kareler oluştururlar.

Anahtar kareler, bir nesnenin boyutunu, yönünü, şeklini veya diğer özelliklerini değiştirdiği önemli çerçevelerdir. Bilgisayar daha sonra aradaki tüm kareleri belirler ve animatör için çok fazla zaman kazandırır. Aşağıdaki resimler, kullanıcı tarafından çizilen çerçeveleri ve bilgisayar tarafından oluşturulan çerçeveleri tasvir etmektedir.

Morphing

Nesne şekillerinin bir formdan diğerine dönüştürülmesine morphing denir. En karmaşık dönüşümlerden biridir.

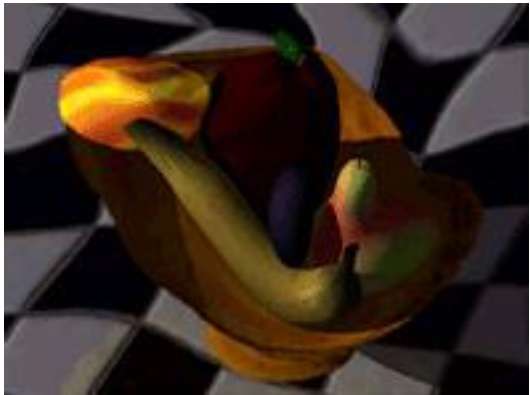
Morf, iki görüntü çok akıcı bir hareketle birbirine karışıyormuş gibi görünür. Teknik açıdan, iki görüntü bozulur ve aralarında bir solma meydana gelir.