Daire Oluşturma Algoritması
Ekranda daire çizmek, çizgi çizmekten biraz daha karmaşıktır. Bir daire oluşturmak için iki popüler algoritma vardır -Bresenham’s Algorithm ve Midpoint Circle Algorithm. Bu algoritmalar, daireyi çizmek için gerekli olan sonraki noktaları belirleme fikrine dayanmaktadır. Algoritmaları ayrıntılı olarak tartışalım -
Dairenin denklemi $ X ^ {2} + Y ^ {2} = r ^ {2}, $ burada r yarıçaptır.
Bresenham Algoritması
Tarama ekranında sürekli bir yay görüntüleyemiyoruz. Bunun yerine yayı tamamlamak için en yakın piksel konumunu seçmeliyiz.
Aşağıdaki resimden, pikseli (X, Y) konumuna koyduğumuzu ve şimdi bir sonraki pikseli nereye koyacağımıza karar vermemiz gerektiğini görebilirsiniz - N (X + 1, Y) veya S (X + 1, Y-1).
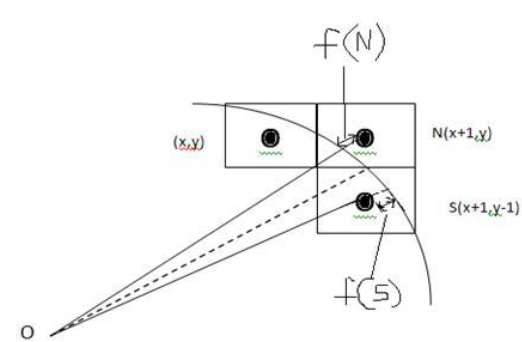
Buna karar parametresi ile karar verilebilir d.
- D <= 0 ise, sonraki piksel olarak N (X + 1, Y) seçilecektir.
- D> 0 ise, sonraki piksel olarak S (X + 1, Y-1) seçilecektir.
Algoritma
Step 1- Çemberin ve yarıçapın merkezinin koordinatlarını alın ve bunları sırasıyla x, y ve R'de saklayın. P = 0 ve Q = R olarak ayarlayın.
Step 2 - Karar parametresi D = 3 - 2R'yi ayarlayın.
Step 3 - P ≤ Q iken 8. adımı tekrarlayın.
Step 4 - Çizim Dairesini (X, Y, P, Q) arayın.
Step 5 - P değerini artırın.
Step 6 - D <0 ise D = D + 4P + 6.
Step 7 - Başka Küme R = R - 1, D = D + 4 (PQ) + 10.
Step 8 - Çizim Dairesini (X, Y, P, Q) arayın.
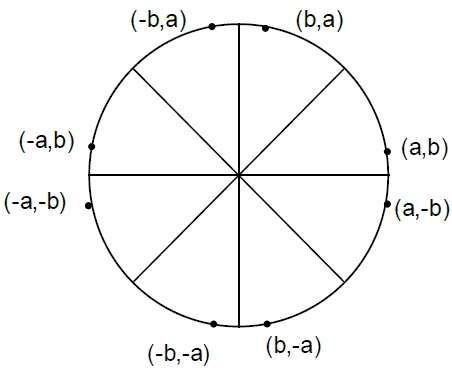
Draw Circle Method(X, Y, P, Q).
Call Putpixel (X + P, Y + Q).
Call Putpixel (X - P, Y + Q).
Call Putpixel (X + P, Y - Q).
Call Putpixel (X - P, Y - Q).
Call Putpixel (X + Q, Y + P).
Call Putpixel (X - Q, Y + P).
Call Putpixel (X + Q, Y - P).
Call Putpixel (X - Q, Y - P).Orta Nokta Algoritması
Step 1 - Giriş yarıçapı r ve $ (x_ {c,} y_ {c}) $ merkezini daire içine alın ve başlangıç noktasında ortalanmış olan dairenin çevresindeki ilk noktayı
(x0, y0) = (0, r)Step 2 - Karar parametresinin başlangıç değerini şu şekilde hesaplayın:
$ P_ {0} $ = 5/4 - r (Bu denklemin basitleştirilmesi için aşağıdaki açıklamaya bakın.)
f(x, y) = x2 + y2 - r2 = 0
f(xi - 1/2 + e, yi + 1)
= (xi - 1/2 + e)2 + (yi + 1)2 - r2
= (xi- 1/2)2 + (yi + 1)2 - r2 + 2(xi - 1/2)e + e2
= f(xi - 1/2, yi + 1) + 2(xi - 1/2)e + e2 = 0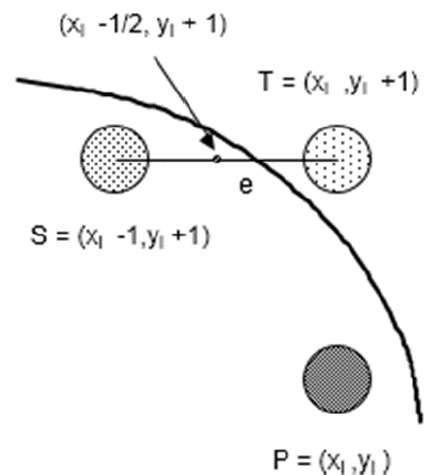
Let di = f(xi - 1/2, yi + 1) = -2(xi - 1/2)e - e2
Thus,
If e < 0 then di > 0 so choose point S = (xi - 1, yi + 1).
di+1 = f(xi - 1 - 1/2, yi + 1 + 1) = ((xi - 1/2) - 1)2 + ((yi + 1) + 1)2 - r2
= di - 2(xi - 1) + 2(yi + 1) + 1
= di + 2(yi + 1 - xi + 1) + 1
If e >= 0 then di <= 0 so choose point T = (xi, yi + 1)
di+1 = f(xi - 1/2, yi + 1 + 1)
= di + 2yi+1 + 1
The initial value of di is
d0 = f(r - 1/2, 0 + 1) = (r - 1/2)2 + 12 - r2
= 5/4 - r {1-r can be used if r is an integer}
When point S = (xi - 1, yi + 1) is chosen then
di+1 = di + -2xi+1 + 2yi+1 + 1
When point T = (xi, yi + 1) is chosen then
di+1 = di + 2yi+1 + 1Step 3 - K = 0'dan başlayan her bir $ X_ {K} $ konumunda aşağıdaki testi gerçekleştirin -
If PK < 0 then next point on circle (0,0) is (XK+1,YK) and
PK+1 = PK + 2XK+1 + 1
Else
PK+1 = PK + 2XK+1 + 1 – 2YK+1
Where, 2XK+1 = 2XK+2 and 2YK+1 = 2YK-2.Step 4 - Diğer yedi oktttaki simetri noktalarını belirleyin.
Step 5 - Hesaplanan her piksel konumunu (X, Y) $ (X_ {C,} Y_ {C}) $ üzerinde ortalanmış dairesel yola taşıyın ve koordinat değerlerini çizin.
X = X + XC, Y = Y + YCStep 6 - X> = Y olana kadar 3. ila 5. adımları tekrarlayın.