Bilgisayar Grafik Eğrileri

Bilgisayar grafiklerinde, genellikle ekrana farklı türde nesneler çizmemiz gerekir. Nesneler her zaman düz değildir ve bir nesneyi çizmek için birçok kez eğri çizmemiz gerekir.

Eğri Türleri

Eğri, sonsuz büyüklükte bir nokta kümesidir. Uç noktalar dışında her noktanın iki komşusu vardır. Eğriler genel olarak üç kategoriye ayrılabilir -explicit, implicit, ve parametric curves.

Örtük Eğriler

Örtülü eğri temsilleri, eğri üzerinde bir noktanın olup olmadığını görmek için test edebilen bir prosedür kullanarak bir eğri üzerindeki nokta kümesini tanımlar. Genellikle, örtük bir eğri, formun örtük bir işlevi ile tanımlanır -

f (x, y) = 0

Birden çok değerli eğrileri temsil edebilir (bir x değeri için birden çok y değeri). Yaygın bir örnek, örtük temsili olan çemberdir.

x² + y² - R² = 0

Açık Eğriler

Bir matematiksel fonksiyon y = f (x) bir eğri olarak çizilebilir. Böyle bir fonksiyon, eğrinin açık temsilidir. Açık gösterim genel değildir çünkü dikey çizgileri temsil edemez ve ayrıca tek değerlidir. Her x değeri için, normalde işlev tarafından yalnızca tek bir y değeri hesaplanır.

Parametrik Eğriler

Parametrik biçime sahip eğrilere parametrik eğriler denir. Açık ve örtük eğri gösterimleri yalnızca işlev bilindiğinde kullanılabilir. Uygulamada parametrik eğriler kullanılır. İki boyutlu bir parametrik eğri aşağıdaki forma sahiptir -

P (t) = f (t), g (t) veya P (t) = x (t), y (t)

F ve g fonksiyonları, eğri üzerindeki herhangi bir noktanın (x, y) koordinatları haline gelir ve noktalar, t parametresi belirli bir aralık [a, b], normalde [0, 1] boyunca değiştirildiğinde elde edilir.

Bezier Eğrileri

Bezier eğrisi Fransız mühendis tarafından keşfedildi Pierre Bézier. Bu eğriler, diğer noktaların kontrolü altında oluşturulabilir. Eğri oluşturmak için kontrol noktaları kullanılarak yaklaşık teğetler kullanılır. Bezier eğrisi matematiksel olarak şu şekilde gösterilebilir:

$$ \ sum_ {k = 0} ^ {n} P_ {i} {B_ {i} ^ {n}} (t) $$

$ P_ {i} $ nokta kümesidir ve $ {B_ {i} ^ {n}} (t) $, - ile verilen Bernstein polinomlarını temsil eder.

$$ {B_ {i} ^ {n}} (t) = \ binom {n} {i} (1 - t) ^ {ni} t ^ {i} $$

Nerede n polinom derecesi, i endeks ve t değişkendir.

En basit Bézier eğrisi, $ P_ {0} $ ile $ P_ {1} $ arasındaki düz çizgidir. İkinci dereceden bir Bezier eğrisi, üç kontrol noktası ile belirlenir. Kübik Bezier eğrisi, dört kontrol noktası tarafından belirlenir.

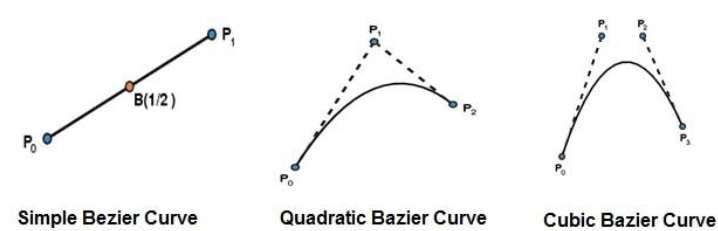
Bezier Eğrilerinin Özellikleri

Bezier eğrileri aşağıdaki özelliklere sahiptir -

Genellikle, kontrol noktalarını birleştiren segmentlerden oluşan kontrol poligonunun şeklini takip ederler.
Her zaman ilk ve son kontrol noktalarından geçerler.
Tanımlayıcı kontrol noktalarının dışbükey gövdesinde bulunurlar.
Eğri parçasını tanımlayan polinomun derecesi, tanımlayan çokgen noktasının sayısından bir eksiktir. Bu nedenle, 4 kontrol noktası için, polinomun derecesi 3'tür, yani kübik polinomdur.
Bir Bezier eğrisi genellikle tanımlayıcı çokgenin şeklini takip eder.
Uç noktalardaki teğet vektörün yönü, ilk ve son bölümler tarafından belirlenen vektörün yönü ile aynıdır.
Bezier eğrisinin dışbükey gövde özelliği, polinomun kontrol noktalarını sorunsuz bir şekilde takip etmesini sağlar.
Hiçbir düz çizgi, bir Bezier eğrisini, kontrol çokgeniyle kesiştiğinden daha fazla kesemez.
Afin bir dönüşüm altında değişmezler.
Bezier eğrileri küresel kontrol gösterir, bir kontrol noktasını hareket ettirmek tüm eğrinin şeklini değiştirir.
Belirli bir Bezier eğrisi, t = t0 noktasında, t = t0 parametre değerine karşılık gelen noktada birleşen iki Bezier segmentine bölünebilir.

B-Spline Eğrileri

Bernstein temel işlevi tarafından üretilen Bezier eğrisi sınırlı esnekliğe sahiptir.

İlk olarak, belirtilen çokgen köşelerinin sayısı, eğriyi tanımlayan sonuçta elde edilen polinomun sırasını sabitler.
İkinci sınırlayıcı özellik, harmanlama fonksiyonunun değerinin, tüm eğri boyunca tüm parametre değerleri için sıfır olmamasıdır.

B-spline temeli, özel durum olarak Bernstein temelini içerir. B-spline temeli global değildir.

Bir B-spline eğrisi, Pi ve B-spline temel fonksiyonu $ N_ {i,} $ k (t) kontrol noktalarının doğrusal bir kombinasyonu olarak tanımlanır.

$ C (t) = \ sum_ {i = 0} ^ {n} P_ {i} N_ {i, k} (t), $ $ n \ geq k-1, $ $ t \: \ epsilon \: [ tk-1, tn + 1] $

Nerede,

{$ p_ {i} $: i = 0, 1, 2… .n} kontrol noktalarıdır
k, B-spline eğrisinin polinom segmentlerinin sırasıdır. K sırası, eğrinin k - 1 dereceli parçalı polinom bölümlerinden oluştuğu anlamına gelir,
$ N_ {i, k} (t) $ “normalleştirilmiş B-spline karıştırma fonksiyonlarıdır”. Bunlar k sırası ile ve normalde "düğüm dizisi" olarak adlandırılan azalan olmayan bir gerçek sayı dizisi ile tanımlanır.

$$ {t_ {i}: i = 0, ... n + K} $$

N _i , k işlevleri aşağıdaki şekilde açıklanmıştır -

$$ N_ {i, 1} (t) = \ left \ {\ begin {matrix} 1, & if \: u \: \ epsilon \: [t_ {i,} t_ {i + 1}) \\ 0 , & Aksi takdirde \ end {matrix} \ right. $$

ve k> 1 ise,

$$ N_ {i, k} (t) = \ frac {t-t_ {i}} {t_ {i + k-1}} N_ {i, k-1} (t) + \ frac {t_ {i + k} -t} {t_ {i + k} - t_ {i + 1}} N_ {i + 1, k-1} (t) $$

$$ t \: \ epsilon \: [t_ {k-1}, t_ {n + 1}) $$

B-spline Eğrisinin Özellikleri

B-spline eğrileri aşağıdaki özelliklere sahiptir -

Herhangi bir parametre değeri için B-spline temel fonksiyonlarının toplamı 1'dir.
Her temel fonksiyon, tüm parametre değerleri için pozitif veya sıfırdır.
Her temel fonksiyon, k = 1 dışında tam olarak bir maksimum değere sahiptir.
Eğrinin maksimum sırası, çokgeni tanımlayan köşe sayısına eşittir.
B-spline polinomunun derecesi, tanımlayan çokgenin köşe sayısından bağımsızdır.
B-spline, eğri yüzeyi üzerinde yerel kontrole izin verir çünkü her köşe, bir eğrinin şeklini yalnızca ilişkili temel fonksiyonunun sıfır olmadığı bir dizi parametre değeri üzerinde etkiler.
Eğri, varyasyonu azaltıcı özelliği sergiler.
Eğri genellikle tanımlayıcı çokgen şeklini takip eder.
Eğriyi tanımlayan çokgenin köşelerine uygulanarak herhangi bir afin dönüşüm uygulanabilir.
Tanımlayıcı çokgeninin dışbükey gövdesi içindeki eğri çizgisi.