Kontrol Sistemleri - Blok Diyagram Cebiri
Blok diyagram cebiri, blok diyagramın temel unsurlarıyla ilgili cebirden başka bir şey değildir. Bu cebir, cebirsel denklemlerin resimsel gösterimi ile ilgilidir.
Bloklar için Temel Bağlantılar
İki blok arasında üç temel bağlantı türü vardır.
Seri Bağlantı
Seri bağlantı da denir cascade connection. Aşağıdaki şekilde, $ G_1 (s) $ ve $ G_2 (s) $ transfer fonksiyonlarına sahip iki blok seri olarak bağlanmıştır.

Bu kombinasyon için $ Y (s) $ çıktısını şu şekilde alacağız:
$$ Y (ler) = G_2 Z (s) $$
$ Z (s) = G_1 (s) X (s) $
$$ \ Rightarrow Y (s) = G_2 (s) [G_1 (s) X (s)] = G_1 (s) G_2 (s) X (s) $$
$$ \ Rightarrow Y (s) = \ lbrace G_1 (s) G_2 (s) \ rbrace X (s) $$
Bu denklemi çıktı denkleminin standart formuyla karşılaştırın, $ Y (s) = G (s) X (s) $. Nerede, $ G (s) = G_1 (s) G_2 (s) $.
Bu, temsil edebileceğimiz anlamına gelir series connectiontek bloklu iki blok. Bu tek bloğun transfer fonksiyonu,product of the transfer functionsbu iki bloktan. Eşdeğer blok şeması aşağıda gösterilmiştir.
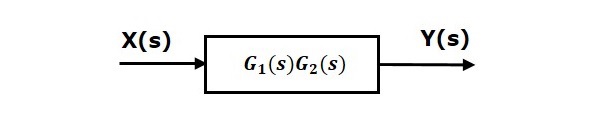
Benzer şekilde, 'n' bloğunun seri bağlantısını tek bir blokla temsil edebilirsiniz. Bu tek bloğun transfer fonksiyonu, tüm bu 'n' bloklarının transfer fonksiyonlarının ürünüdür.
Paralel bağlantı
Bağlı olan bloklar parallel sahip olacak same input. Aşağıdaki şekilde, $ G_1 (s) $ ve $ G_2 (s) $ transfer fonksiyonlarına sahip iki blok paralel olarak bağlanmıştır. Bu iki bloğun çıkışları toplama noktasına bağlıdır.

Bu kombinasyon için $ Y (s) $ çıktısını şu şekilde alacağız:
$$ Y = Y_1 + Y_2 $ $$
Burada, $ Y_1 (s) = G_1 (s) X (s) $ ve $ Y_2 (s) = G_2 (s) X (s) $
$$ \ Rightarrow Y (s) = G_1 (s) X (s) + G_2 (s) X (s) = \ lbrace G_1 (s) + G_2 (s) \ rbrace X (s) $$
Bu denklemi çıktı denkleminin standart formuyla karşılaştırın, $ Y (s) = G (s) X (s) $.
Nerede, $ G (s) = G_1 (s) + G_2 (s) $.
Bu, temsil edebileceğimiz anlamına gelir parallel connectiontek bloklu iki blok. Bu tek bloğun transfer fonksiyonu,sum of the transfer functionsbu iki bloktan. Eşdeğer blok şeması aşağıda gösterilmiştir.

Benzer şekilde, 'n' bloğunun paralel bağlantısını tek bir blokla temsil edebilirsiniz. Bu tek bloğun transfer fonksiyonu, tüm bu 'n' bloklarının transfer fonksiyonlarının cebirsel toplamıdır.
Geri Bildirim Bağlantısı
Önceki bölümlerde tartıştığımız gibi, iki tür feedback- olumlu geribildirim ve olumsuz geri bildirim. Aşağıdaki şekil negatif geri besleme kontrol sistemini göstermektedir. Burada, $ G (s) $ ve $ H (s) $ transfer fonksiyonlarına sahip iki blok kapalı bir döngü oluşturur.

Toplama noktasının çıktısı -
$$ E (s) = X (s) -H (s) Y (s) $$
$ Y (s) $ çıktısı -
$$ Y (s) = E (s) G (s) $$
Yukarıdaki denklemde $ E (s) $ değerini değiştirin.
$$ Y (s) = \ sol \ {X (s) -H (s) Y (s) \ rbrace G (s) \ sağ \} $$
$$ Y (s) \ sol \ {1 + G (s) H (s) \ rbrace = X (s) G (s) \ sağ \} $$
$$ \ Rightarrow \ frac {Y (s)} {X (s)} = \ frac {G (s)} {1 + G (s) H (s)} $$
Bu nedenle, negatif geri besleme kapalı döngü aktarım işlevi $ \ frac {G (s)} {1 + G (s) H (s)} $ şeklindedir.
Bu, iki bloğun negatif geri besleme bağlantısını tek bir blokla temsil edebileceğimiz anlamına gelir. Bu tek bloğun transfer fonksiyonu, negatif geri beslemenin kapalı döngü transfer fonksiyonudur. Eşdeğer blok şeması aşağıda gösterilmiştir.

Benzer şekilde, iki bloğun pozitif geri besleme bağlantısını tek bir blokla temsil edebilirsiniz. Bu tek bloğun transfer fonksiyonu, pozitif geri beslemenin kapalı döngü transfer fonksiyonudur, yani $ \ frac {G (s)} {1-G (s) H (s)} $
Toplama Noktaları için Blok Şeması Cebiri
Bloklara göre toplama noktalarını değiştirmenin iki olasılığı vardır -
- Bloktan sonra değişen toplama noktası
- Bloktan önce toplama noktasının değiştirilmesi
Şimdi yukarıdaki iki durumda tek tek ne tür düzenlemelerin yapılması gerektiğini görelim.
Bloktan Sonra Toplama Noktasını Kaydırma
Aşağıdaki şekilde gösterilen blok şemayı düşünün. Burada, toplama noktası bloktan önce mevcuttur.

Toplama noktasının iki girişi vardır $ R (s) $ ve $ X (s) $. Bunun çıktısı $ \ left \ {R (s) + X (s) \ right \} $ şeklindedir.
Dolayısıyla, $ G (s) $ bloğunun girdisi $ \ left \ {R (s) + X (s) \ right \} $ ve bunun çıktısı -
$$ Y (s) = G (s) \ sol \ {R (s) + X (s) \ sağ \} $$
$ \ Rightarrow Y (s) = G (s) R (s) + G (s) X (s) $ (Equation 1)
Şimdi, toplama noktasını bloktan sonra kaydırın. Bu blok diyagram aşağıdaki şekilde gösterilmektedir.

$ G (s) $ bloğunun çıktısı $ G (s) R (s) $ 'dır.
Toplama noktasının çıktısı
$ Y (s) = G (s) R (s) + X (s) $ (Equation 2)
Denklem 1 ve Denklem 2'yi karşılaştırın.
İlk terim $ 'G (s) R (s)' $ her iki denklemde de aynıdır. Ancak ikinci dönemde farklılık var. İkinci terimi de aynı hale getirmek için, bir tane daha $ G (s) $ bloğuna ihtiyacımız var. $ X (s) $ girdisine sahip ve bu bloğun çıktısı $ X (s) $ yerine toplama noktasına girdi olarak veriliyor. Bu blok diyagram aşağıdaki şekilde gösterilmektedir.
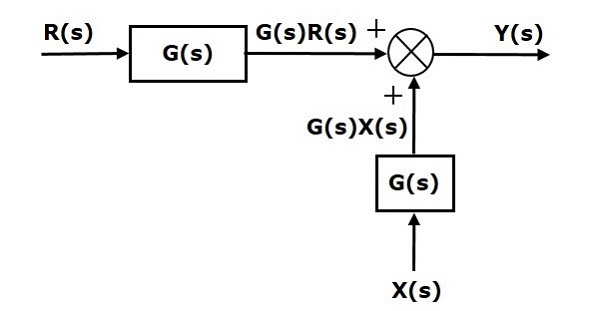
Toplama Noktasını Bloktan Önce Kaydırma
Aşağıdaki şekilde gösterilen blok şemayı düşünün. Burada, toplama noktası bloktan sonra mevcuttur.

Bu blok diyagramın çıktısı -
$ Y (s) = G (s) R (s) + X (s) $ (Equation 3)
Şimdi, toplama noktasını bloktan önce kaydırın. Bu blok diyagram aşağıdaki şekilde gösterilmektedir.

Bu blok diyagramın çıktısı -
$ Y (S) = G (s) R (s) + G (s) X (s) $ (Equation 4)
Denklem 3 ve Denklem 4'ü karşılaştırın,
İlk terim $ 'G (s) R (s)' $ her iki denklemde de aynıdır. Ancak ikinci dönemde farklılık var. İkinci terimi de aynı elde etmek için, bir tane daha $ \ frac {1} {G (s)} $ bloğuna ihtiyacımız var. $ X (s) $ girdisine sahip ve bu bloğun çıktısı $ X (s) $ yerine toplama noktasına girdi olarak veriliyor. Bu blok diyagram aşağıdaki şekilde gösterilmektedir.

Kalkış Noktaları için Blok Şeması Cebiri
Kalkış noktalarını bloklara göre kaydırmanın iki olasılığı vardır -
- Bloktan sonra kalkış noktasının kaydırılması
- Kalkış noktasının bloktan önce kaydırılması
Şimdi yukarıdaki iki durumda tek tek ne tür düzenlemeler yapılacağını görelim.
Bloktan Sonra Kalkış Noktasının Değiştirilmesi
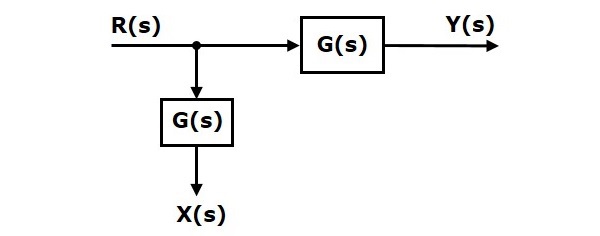
Aşağıdaki şekilde gösterilen blok şemayı düşünün. Bu durumda kalkış noktası bloktan önce mevcuttur.

Burada, $ X (s) = R (s) $ ve $ Y (s) = G (s) R (s) $
Kalkış noktasını bloktan sonra kaydırdığınızda, $ Y (s) $ çıkışı aynı olacaktır. Ancak $ X (s) $ değerinde fark var. Dolayısıyla, aynı $ X (s) $ değerini elde etmek için, bir blok daha $ \ frac {1} {G (s)} $ gerekiyor. $ Y (s) $ girdisine sahip ve çıktı $ X (s) $. Bu blok diyagram aşağıdaki şekilde gösterilmektedir.

Kalkış Noktasının Bloktan Önce Kaydırılması
Aşağıdaki şekilde gösterilen blok şemayı düşünün. Burada kalkış noktası bloktan sonra mevcuttur.

Burada, $ X (s) = Y (s) = G (s) R (s) $
Kalkış noktasını bloktan önce kaydırdığınızda, $ Y (s) $ çıkışı aynı olacaktır. Ancak $ X (s) $ değerinde fark var. Dolayısıyla, aynı $ X (s) $ değerini elde etmek için, bir tane daha $ G (s) $ bloğuna ihtiyacımız var. $ R (s) $ girdisine sahip ve çıktı $ X (s) $. Bu blok diyagram aşağıdaki şekilde gösterilmektedir.