Kontrol Sistemleri - Zaman Tepki Analizi
Kontrol sistemlerinin tepkisini hem zaman alanında hem de frekans alanında analiz edebiliriz. Daha sonraki bölümlerde kontrol sistemlerinin frekans yanıt analizini tartışacağız. Şimdi kontrol sistemlerinin zaman yanıt analizini tartışalım.
Zaman Tepkisi nedir?
Bir giriş için kontrol sisteminin çıkışı zamana göre değişiklik gösteriyorsa, buna time responsekontrol sisteminin. Zaman cevabı iki bölümden oluşur.
- Geçici tepki
- Kararlı durum yanıtı
Kontrol sisteminin zaman alanındaki tepkisi aşağıdaki şekilde gösterilmiştir.

Burada hem geçici hem de sabit durumlar şekilde gösterilmektedir. Bu durumlara karşılık gelen yanıtlar, geçici ve sabit durum yanıtları olarak bilinir.
Matematiksel olarak, c (t) zaman yanıtını şu şekilde yazabiliriz:
$$ c (t) = c_ {tr} (t) + c_ {ss} (t) $$
Nerede,
- c tr (t) geçici yanıttır
- c ss (t) kararlı durum cevabıdır
Geçici tepki
Kontrol sistemine girdi uyguladıktan sonra, çıkışın kararlı duruma ulaşması belirli bir zaman alır. Böylece, sabit bir duruma geçene kadar çıkış geçici durumda olacaktır. Bu nedenle, geçici durum sırasında kontrol sisteminin tepkisi olarak bilinirtransient response.
Büyük 't' değerleri için geçici yanıt sıfır olacaktır. İdeal olarak, bu 't' değeri sonsuzdur ve pratikte beş kat sabittir.
Matematiksel olarak şöyle yazabiliriz
$$ \ lim_ {t \ rightarrow \ infty} c_ {tr} (t) = 0 $$
Kararlı durum tepkisi
Büyük 't' değerleri için geçici yanıt sıfır değerine sahip olduktan sonra bile kalan zaman yanıtının parçası olarak bilinir steady state response. Bu, geçici yanıtın sabit durumda bile sıfır olacağı anlamına gelir.
Example
$ C (t) = 10 + 5e ^ {- t} $ kontrol sisteminin zaman cevabının geçici ve sabit durum terimlerini bulalım
Burada, ikinci terim $ 5e ^ {- t} $ şu şekilde sıfır olacaktır: tsonsuzluğu belirtir. Yani, butransient term. Ve ilk 10 terim şu şekilde kalır:tsonsuza yaklaşır. Yani, busteady state term.
Standart Test Sinyalleri
Standart test sinyalleri impuls, adım, rampa ve paraboliktir. Bu sinyaller, çıkışın zaman yanıtını kullanarak kontrol sistemlerinin performansını bilmek için kullanılır.
Birim Darbe Sinyali
Bir birim dürtü sinyali, δ (t) olarak tanımlanır
$ \ delta (t) = 0 $, $ t \ neq 0 $ için
ve $ \ int_ {0 ^ -} ^ {0 ^ +} \ delta (t) dt = 1 $
Aşağıdaki şekil birim darbe sinyalini göstermektedir.

Dolayısıyla, birim dürtü sinyali yalnızca 't' sıfıra eşit olduğunda mevcuttur. Bu sinyalin alanı 't' etrafında küçük bir zaman aralığı altında sıfıra eşittir birdir. Birim dürtü sinyalinin değeri, diğer tüm 't' değerleri için sıfırdır.
Birim Adım Sinyali
Bir birim adım sinyali, u (t) olarak tanımlanır
$$ u (t) = 1; t \ geq 0 $$
$ = 0; t <0 $
Aşağıdaki şekil birim adım sinyalini göstermektedir.

Dolayısıyla, sıfır dahil tüm pozitif 't' değerleri için birim adım sinyali mevcuttur. Ve değeri bu aralıkta birdir. Birim adım sinyalinin değeri, "t" nin tüm negatif değerleri için sıfırdır.
Birim Rampa Sinyali
Bir birim rampa sinyali, r (t) şu şekilde tanımlanır:
$$ r (t) = t; t \ geq 0 $$
$ = 0; t <0 $
Birim rampa sinyali, birim adım sinyali cinsinden $ r (t) $, $ u (t) $ as
$$ r (t) = tu (t) $$
Aşağıdaki şekil birim rampa sinyalini göstermektedir.

Dolayısıyla, sıfır dahil tüm pozitif 't' değerleri için birim rampa sinyali mevcuttur. Ve değeri bu aralıkta 't'ye göre doğrusal olarak artar. Birim rampa sinyalinin değeri, 't'nin tüm negatif değerleri için sıfırdır.
Birim Parabolik Sinyal
Bir birim parabolik sinyal, p (t) şu şekilde tanımlanır:
$$ p (t) = \ frac {t ^ 2} {2}; t \ geq 0 $$
$ = 0; t <0 $
Birim parabolik sinyali, birim adım sinyali cinsinden $ p (t) $, $ u (t) $ as,
$$ p (t) = \ frac {t ^ 2} {2} u (t) $$
Aşağıdaki şekil birim parabolik sinyali gösterir.
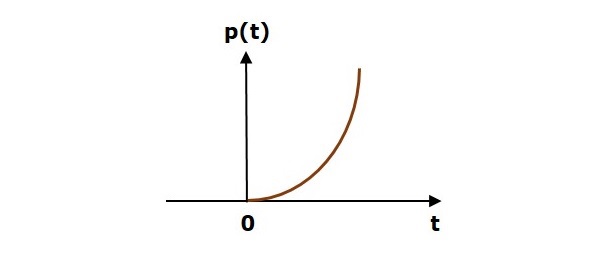
Bu nedenle, birim parabolik sinyalin tüm pozitif değerleri için mevcuttur. ‘t’sıfır dahil. Ve değeri bu aralıkta 't'ye göre doğrusal olmayan bir şekilde artar. Birim parabolik sinyalin değeri, "t" nin tüm negatif değerleri için sıfırdır.