Mekanik Sistemlerin Elektriksel Analojileri
İki sistemin olduğu söyleniyor analogous Aşağıdaki iki koşul karşılanırsa birbirine.
- İki sistem fiziksel olarak farklı
- Bu iki sistemin diferansiyel denklem modellemesi aynıdır
Elektrik sistemleri ve mekanik sistemler fiziksel olarak farklı iki sistemdir. Öteleme mekanik sistemlerin iki tür elektriksel analojisi vardır. Bunlar kuvvet voltajı analojisi ve kuvvet akımı analojisidir.
Kuvvet Gerilimi Analojisi
Kuvvet gerilim analojisinde, matematiksel denklemler translational mechanical system Elektrik sisteminin örgü denklemleri ile karşılaştırılır.
Aşağıdaki şekilde gösterildiği gibi, aşağıdaki translasyonel mekanik sistemi düşünün.
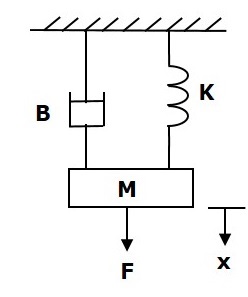
force balanced equation bu sistem için
$$ F = F_m + F_b + F_k $$
$ \ Rightarrow F = M \ frac {\ text {d} ^ 2x} {\ text {d} t ^ 2} + B \ frac {\ text {d} x} {\ text {d} t} + Kx $ (Equation 1)
Aşağıdaki şekilde gösterildiği gibi aşağıdaki elektrik sistemini düşünün. Bu devre bir direnç, bir indüktör ve bir kapasitörden oluşur. Tüm bu elektriksel elemanlar bir seri olarak bağlanmıştır. Bu devreye uygulanan giriş voltajı $ V $ volt ve devreden akan akım $ i $ Amps'dir.

Bu devre için örgü denklemi
$ V = Ri + L \ frac {\ text {d} i} {\ text {d} t} + \ frac {1} {c} \ int idt $ (Equation 2)
Denklem 2'deki $ i = \ frac {\ text {d} q} {\ text {d} t} $ 'ı değiştirin.
$$ V = R \ frac {\ text {d} q} {\ text {d} t} + L \ frac {\ text {d} ^ 2q} {\ text {d} t ^ 2} + \ frac { q} {C} $$
$ \ Rightarrow V = L \ frac {\ text {d} ^ 2q} {\ text {d} t ^ 2} + R \ frac {\ text {d} q} {\ text {d} t} + \ sol (\ frac {1} {c} \ sağ) q $ (Equation 3)
Denklem 1 ve Denklem 3'ü karşılaştırarak, öteleme mekanik sistem ve elektrik sisteminin analog miktarlarını elde edeceğiz. Aşağıdaki tablo bu benzer büyüklükleri göstermektedir.
| Öteleme Mekanik Sistem | Elektrik sistemi |
|---|---|
| Kuvvet (F) | Gerilim (V) |
| Kütle (M) | Endüktans (L) |
| Sürtünme Katsayısı (B) | Direnç (R) |
| Yay Sabiti (K) | Karşılıklı Kapasitans $ (\ frac {1} {c}) $ |
| Yer değiştirme (x) | Şarj (q) |
| Hız (v) | Akım (i) |
Benzer şekilde, rotasyonel mekanik sistemler için tork voltajı analojisi vardır. Şimdi bu benzetmeyi tartışalım.
Tork Gerilimi Analojisi
Bu benzetmede, matematiksel denklemler rotational mechanical system Elektrik sisteminin örgü denklemleri ile karşılaştırılır.
Rotasyonel mekanik sistem aşağıdaki şekilde gösterilmektedir.

Tork dengeli denklem
$$ T = T_j + T_b + T_k $$
$ \ Rightarrow T = J \ frac {\ text {d} ^ 2 \ theta} {\ text {d} t ^ 2} + B \ frac {\ text {d} \ theta} {\ text {d} t} + k \ theta $ (Equation 4)
Denklem 4 ve Denklem 3'ü karşılaştırarak, döner mekanik sistem ve elektrik sisteminin benzer miktarlarını elde edeceğiz. Aşağıdaki tablo bu benzer büyüklükleri göstermektedir.
| Rotasyonel Mekanik Sistem | Elektrik sistemi |
|---|---|
| Tork (T) | Gerilim (V) |
| Atalet Momenti (J) | Endüktans (L) |
| Dönme sürtünme katsayısı (B) | Direnç (R) |
| Burulma yay sabiti (K) | Karşılıklı Kapasitans $ (\ frac {1} {c}) $ |
| Açısal Yer Değiştirme (θ) | Şarj (q) |
| Açısal Hız (ω) | Akım (i) |
Geçerli Analojiyi Zorla
Kuvvet akım analojisinde, matematiksel denklemler translational mechanical system elektrik sisteminin düğüm denklemleri ile karşılaştırılır.
Aşağıdaki şekilde gösterildiği gibi aşağıdaki elektrik sistemini düşünün. Bu devre akım kaynağı, direnç, indüktör ve kapasitörden oluşur. Tüm bu elektriksel elemanlar paralel olarak bağlanmıştır.

Düğüm denklemi
$ i = \ frac {V} {R} + \ frac {1} {L} \ int Vdt + C \ frac {\ text {d} V} {\ text {d} t} $ (Equation 5)
Denklem 5'teki $ V = \ frac {\ text {d} \ Psi} {\ text {d} t} $ yerine koyun.
$$ i = \ frac {1} {R} \ frac {\ text {d} \ Psi} {\ text {d} t} + \ left (\ frac {1} {L} \ right) \ Psi + C \ frac {\ text {d} ^ 2 \ Psi} {\ text {d} t ^ 2} $$
$ \ Rightarrow i = C \ frac {\ text {d} ^ 2 \ Psi} {\ text {d} t ^ 2} + \ left (\ frac {1} {R} \ right) \ frac {\ text { d} \ Psi} {\ text {d} t} + \ left (\ frac {1} {L} \ right) \ Psi $ (Equation 6)
Denklem 1 ve Denklem 6'yı karşılaştırarak, translasyonel mekanik sistem ve elektrik sisteminin analog miktarlarını elde edeceğiz. Aşağıdaki tablo bu benzer büyüklükleri göstermektedir.
| Öteleme Mekanik Sistem | Elektrik sistemi |
|---|---|
| Kuvvet (F) | Akım (i) |
| Kütle (M) | Kapasite (C) |
| Sürtünme katsayısı (B) | Karşılıklı Direnç $ (\ frac {1} {R}) $ |
| Yay sabiti (K) | Karşılıklı Endüktans $ (\ frac {1} {L}) $ |
| Yer değiştirme (x) | Manyetik Akı (ψ) |
| Hız (v) | Gerilim (V) |
Benzer şekilde, rotasyonel mekanik sistemler için bir tork akımı analojisi vardır. Şimdi bu benzetmeyi tartışalım.
Tork Akımı Analojisi
Bu benzetmede, matematiksel denklemler rotational mechanical system elektrik sisteminin düğümlü ağ denklemleri ile karşılaştırılır.
Denklem 4 ve Denklem 6'yı karşılaştırarak, döner mekanik sistem ve elektrik sisteminin benzer miktarlarını elde edeceğiz. Aşağıdaki tablo bu benzer büyüklükleri göstermektedir.
| Rotasyonel Mekanik Sistem | Elektrik sistemi |
|---|---|
| Tork (T) | Akım (i) |
| Eylemsizlik momenti (J) | Kapasite (C) |
| Dönme sürtünme katsayısı (B) | Karşılıklı Direnç $ (\ frac {1} {R}) $ |
| Burulma yay sabiti (K) | Karşılıklı Endüktans $ (\ frac {1} {L}) $ |
| Açısal yer değiştirme (θ) | Manyetik akı (ψ) |
| Açısal hız (ω) | Gerilim (V) |
Bu bölümde, mekanik sistemlerin elektriksel benzerliklerini tartıştık. Bu benzetmeler, analog elektrik sisteminden mekanik sistem gibi elektriksel olmayan sistemi incelemek ve analiz etmek için yararlıdır.