Kontrol Sistemleri - Hızlı Kılavuz
Kontrol sistemi, çıkışı kontrol ederek istenilen yanıtı sağlayan bir sistemdir. Aşağıdaki şekil bir kontrol sisteminin basit blok şemasını göstermektedir.

Burada kontrol sistemi tek bir blokla temsil edilmektedir. Çıkış değişken girişlerle kontrol edildiğinden, kontrol sistemi bu adı almıştır. Bu girdiyi bazı mekanizmalarla değiştireceğiz. Açık döngü ve kapalı döngü kontrol sistemleri ile ilgili bir sonraki bölümde, istenen yanıtı elde etmek için kontrol sistemi içindeki blokları ve bu girdiyi nasıl değiştireceğimizi detaylı olarak inceleyeceğiz.
Examples - Trafik ışıkları kontrol sistemi, çamaşır makinesi
Traffic lights control systembir kontrol sistemi örneğidir. Burada, bu kontrol sistemine bir dizi giriş sinyali uygulanır ve çıkış, belirli bir süre yanacak olan üç ışıktan biridir. Bu süre zarfında diğer iki ışık sönecektir. Belirli bir kavşaktaki trafik çalışmasına bağlı olarak, ışıkların açık ve kapalı süreleri belirlenebilir. Buna göre, giriş sinyali çıkışı kontrol eder. Böylece trafik ışıkları kontrol sistemi zamana göre çalışmaktadır.
Kontrol Sistemlerinin Sınıflandırılması
Bazı parametrelere dayanarak, kontrol sistemlerini aşağıdaki şekillerde sınıflandırabiliriz.
Sürekli zaman ve Kesikli Zaman Kontrol Sistemleri
Kontrol Sistemleri, sürekli zamanlı kontrol sistemleri ve ayrık zamanlı kontrol sistemleri olarak sınıflandırılabilir. type of the signal Kullanılmış.
İçinde continuous timekontrol sistemleri, tüm sinyaller zaman içinde süreklidir. Ama içindediscrete time kontrol sistemleri, bir veya daha fazla ayrık zaman sinyali vardır.
SISO ve MIMO Kontrol Sistemleri
Kontrol Sistemleri, SISO kontrol sistemleri ve MIMO kontrol sistemleri olarak sınıflandırılabilir. number of inputs and outputs mevcut.
SISO(Tek Girişli ve Tek Çıkışlı) kontrol sistemleri bir giriş ve bir çıkışa sahiptir. Buna karşılık,MIMO (Çoklu Girişler ve Çoklu Çıkışlar) kontrol sistemlerinin birden fazla girişi ve birden fazla çıkışı vardır.
Açık Döngü ve Kapalı Döngü Kontrol Sistemleri
Kontrol Sistemleri, açık çevrim kontrol sistemleri ve kapalı çevrim kontrol sistemleri olarak sınıflandırılabilir. feedback path.
İçinde open loop control systems, çıktı girişe geri beslenmez. Dolayısıyla, kontrol işlemi istenen çıktıdan bağımsızdır.
Aşağıdaki şekil, açık döngü kontrol sisteminin blok şemasını göstermektedir.

Burada, bir kontrolöre bir giriş uygulanır ve bir çalıştırma sinyali veya kontrol sinyali üretir. Bu sinyal, kontrol edilecek bir tesis veya sürece girdi olarak verilir. Böylece tesis kontrollü bir çıktı üretir. Daha önce tartıştığımız trafik ışıkları kontrol sistemi, bir açık döngü kontrol sistemi örneğidir.
İçinde closed loop control systemsçıkış, girişe geri beslenir. Bu nedenle, kontrol işlemi istenen çıktıya bağlıdır.
Aşağıdaki şekil, negatif geri beslemeli kapalı döngü kontrol sisteminin blok şemasını göstermektedir.
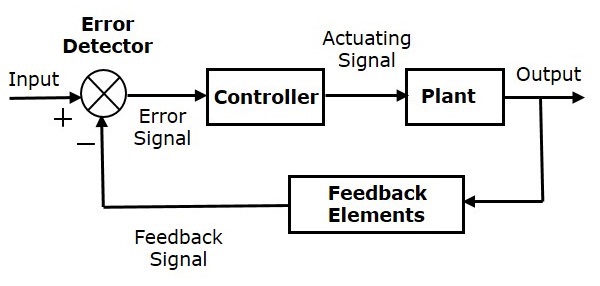
Hata detektörü, giriş ve geri besleme sinyali arasındaki fark olan bir hata sinyali üretir. Bu geri besleme sinyali, tüm sistemin çıktısını bu bloğa bir girdi olarak düşünerek bloktan (geri besleme elemanları) elde edilir. Doğrudan giriş yerine, hata sinyali bir kontrolöre giriş olarak uygulanır.
Böylece, kontrolör tesisi kontrol eden bir çalıştırma sinyali üretir. Bu kombinasyonda, istenen yanıtı elde edene kadar kontrol sisteminin çıkışı otomatik olarak ayarlanır. Bu nedenle, kapalı döngü kontrol sistemlerine otomatik kontrol sistemleri de denir. Girişte sensör bulunan trafik ışıkları kontrol sistemi, kapalı döngü kontrol sistemine bir örnektir.
Açık döngü ve kapalı döngü kontrol sistemleri arasındaki farklar aşağıdaki tabloda belirtilmiştir.
| Açık Döngü Kontrol Sistemleri | Kapalı Çevrim Kontrol Sistemleri |
|---|---|
| Kontrol işlemi istenen çıktıdan bağımsızdır. | Kontrol işlemi istenen çıktıya bağlıdır. |
| Geri bildirim yolu mevcut değil. | Geri bildirim yolu mevcut. |
| Bunlar aynı zamanda non-feedback control systems. | Bunlar aynı zamanda feedback control systems. |
| Tasarımı kolay. | Tasarımı zor. |
| Bunlar ekonomiktir. | Bunlar daha pahalıdır. |
| Yanlış. | Doğru. |
Çıktı veya çıktının bir kısmı giriş tarafına döndürülür ve sistem girdisinin bir parçası olarak kullanılırsa, o zaman feedback. Geri bildirim, kontrol sistemlerinin performansını iyileştirmek için önemli bir rol oynar. Bu bölümde, geribildirim türlerini ve geri bildirimlerin etkilerini tartışalım.
Geri Bildirim Türleri
İki tür geri bildirim vardır -
- Olumlu geribildirim
- Olumsuz geribildirim
Olumlu geribildirim
Olumlu geri bildirim, referans girişini ekler, $R(s)$ve geri bildirim çıkışı. Aşağıdaki şekil blok şemasını göstermektedir.positive feedback control system.

Transfer fonksiyonu kavramı sonraki bölümlerde tartışılacaktır. Şimdilik, pozitif geri besleme kontrol sisteminin transfer fonksiyonunun,
$T=\frac{G}{1-GH}$ (Denklem 1)
Nerede,
T pozitif geri besleme kontrol sisteminin transfer fonksiyonu veya toplam kazancıdır.
G frekansın bir fonksiyonu olan açık döngü kazancıdır.
H frekansın bir fonksiyonu olan geri besleme yolunun kazancıdır.
Olumsuz geribildirim
Negatif geri besleme, referans girişi arasındaki hatayı azaltır, $R(s)$ve sistem çıkışı. Aşağıdaki şekil, cihazın blok şemasını göstermektedir.negative feedback control system.

Negatif geri besleme kontrol sisteminin transfer işlevi,
$T=\frac{G}{1+GH}$ (Denklem 2)
Nerede,
T negatif geri besleme kontrol sisteminin transfer fonksiyonu veya toplam kazancıdır.
G frekansın bir fonksiyonu olan açık döngü kazancıdır.
H frekansın bir fonksiyonu olan geri besleme yolunun kazancıdır.
Yukarıdaki transfer fonksiyonunun türetilmesi sonraki bölümlerde mevcuttur.
Geri Bildirimin Etkileri
Şimdi geri bildirimin etkilerini anlayalım.
Geribildirimin Genel Kazanç Üzerindeki Etkisi
Denklem 2'den, negatif geri beslemeli kapalı döngü kontrol sisteminin genel kazancının 'G' ve (1 + GH) oranı olduğunu söyleyebiliriz. Dolayısıyla, genel kazanç (1 + GH) değerine bağlı olarak artabilir veya azalabilir.
(1 + GH) değeri 1'den küçükse, genel kazanç artar. Bu durumda, 'GH' değeri negatiftir çünkü geri besleme yolunun kazancı negatiftir.
(1 + GH) değeri 1'den büyükse, genel kazanç azalır. Bu durumda 'GH' değeri pozitiftir çünkü geri besleme yolunun kazancı pozitiftir.
Genel olarak, 'G' ve 'H' frekansın işlevleridir. Böylece geri besleme, bir frekans aralığında sistemin toplam kazancını artıracak ve diğer frekans aralığında azalacaktır.
Geribildirimin Duyarlılık Üzerindeki Etkisi
Sensitivity negatif geri beslemeli kapalı döngü kontrol sisteminin toplam kazancının (T) açık döngü kazancındaki varyasyona (G) olarak tanımlanır
$S_{G}^{T} = \frac{\frac{\partial T}{T}}{\frac{\partial G}{G}}=\frac{Percentage\: change \: in \:T}{Percentage\: change \: in \:G}$ (Denklem 3)
Nerede, ∂T G'deki artan değişiklik nedeniyle T'deki artımlı değişikliktir.
Denklem 3'ü şu şekilde yeniden yazabiliriz:
$S_{G}^{T}=\frac{\partial T}{\partial G}\frac{G}{T}$ (Denklem 4)
Denklem 2'nin her iki tarafında G'ye göre kısmi farklılaşma yapın.
$\frac{\partial T}{\partial G}=\frac{\partial}{\partial G}\left (\frac{G}{1+GH} \right )=\frac{(1+GH).1-G(H)}{(1+GH)^2}=\frac{1}{(1+GH)^2}$ (Denklem 5)
Denklem 2'den alacaksın
$\frac{G}{T}=1+GH$ (Denklem 6)
Denklem 4'teki Denklem 5 ve Denklem 6'yı değiştirin.
$$S_{G}^{T}=\frac{1}{(1+GH)^2}(1+GH)=\frac{1}{1+GH}$$
Yani, biz var sensitivity(1 + GH) 'nin tersi olarak kapalı döngü kontrol sisteminin toplam kazancının Dolayısıyla (1 + GH) değerine bağlı olarak Duyarlılık artabilir veya azalabilir.
(1 + GH) değeri 1'den küçükse duyarlılık artar. Bu durumda, 'GH' değeri negatiftir çünkü geri besleme yolunun kazancı negatiftir.
(1 + GH) değeri 1'den büyükse duyarlılık azalır. Bu durumda 'GH' değeri pozitiftir çünkü geribildirim yolunun kazanımı pozitiftir.
Genel olarak, 'G' ve 'H' frekansın işlevleridir. Böylece geri besleme, bir frekans aralığında sistem kazancının hassasiyetini artıracak ve diğer frekans aralığında azalacaktır. Bu nedenle, 'GH' değerlerini, sistemin duyarsız veya parametre değişikliklerine daha az duyarlı olacağı şekilde seçmeliyiz.
Geribildirimin Kararlılık Üzerindeki Etkisi
Çıkışı kontrol altındaysa bir sistemin kararlı olduğu söylenir. Aksi takdirde kararsız olduğu söylenir.
Denklem 2'de, payda değeri sıfır ise (yani, GH = -1), o zaman kontrol sisteminin çıktısı sonsuz olacaktır. Böylece kontrol sistemi kararsız hale gelir.
Bu nedenle, kontrol sistemini kararlı hale getirmek için geri bildirimi doğru şekilde seçmemiz gerekir.
Geribildirimin Gürültü Üzerindeki Etkisi
Geri beslemenin gürültü üzerindeki etkisini bilmek için, sadece gürültü sinyalinden kaynaklanan geri beslemeli ve geri beslemesiz transfer fonksiyonu ilişkilerini karşılaştıralım.
Bir düşünün open loop control system aşağıda gösterildiği gibi gürültü sinyali ile.

open loop transfer function tek başına gürültü sinyali nedeniyle
$\frac{C(s)}{N(s)}=G_b$ (Denklem 7)
Diğer girdi yapılarak elde edilir $R(s)$ sıfıra eşit.
Bir düşünün closed loop control system aşağıda gösterildiği gibi gürültü sinyali ile.

closed loop transfer function tek başına gürültü sinyali nedeniyle
$\frac{C(s)}{N(s)}=\frac{G_b}{1+G_aG_bH}$ (Denklem 8)
Diğer girdi yapılarak elde edilir $R(s)$ sıfıra eşit.
Denklem 7 ve Denklem 8'i karşılaştırın,
Kapalı döngü kontrol sisteminde, gürültü sinyalinden kaynaklanan kazanç, bir faktör kadar azaltılır. $(1+G_a G_b H)$ şartı ile $(1+G_a G_b H)$ birden büyüktür.
Kontrol sistemleri olarak bilinen bir dizi matematiksel denklem ile temsil edilebilir. mathematical model. Bu modeller, kontrol sistemlerinin analizi ve tasarımı için kullanışlıdır. Kontrol sisteminin analizi, girdiyi ve matematiksel modeli bildiğimizde çıktıyı bulmak anlamına gelir. Kontrol sisteminin tasarımı, girdi ve çıktıyı bildiğimizde matematiksel modeli bulmak anlamına gelir.
Aşağıdaki matematiksel modeller çoğunlukla kullanılmaktadır.
- Diferansiyel denklem modeli
- Transfer fonksiyonu modeli
- Durum uzayı modeli
Bu bölümde ilk iki modeli tartışalım.
Diferansiyel Denklem Modeli
Diferansiyel denklem modeli, kontrol sistemlerinin zaman alanı matematiksel modelidir. Diferansiyel denklem modeli için şu adımları izleyin.
Verilen kontrol sistemine temel kanunları uygulayın.
Ara değişken (ler) i eleyerek diferansiyel denklemi girdi ve çıktı cinsinden alın.
Misal
Aşağıdaki şekilde gösterildiği gibi aşağıdaki elektrik sistemini düşünün. Bu devre direnç, indüktör ve kapasitörden oluşur. Tüm bu elektriksel elemanlar birbirine bağlıdırseries. Bu devreye uygulanan giriş voltajı$v_i$ ve kapasitördeki voltaj, çıkış voltajıdır $v_o$.

Bu devre için örgü denklemi
$$v_i=Ri+L\frac{\text{d}i}{\text{d}t}+v_o$$
İkame, kapasitörden geçen akım $i=c\frac{\text{d}v_o}{\text{d}t}$ yukarıdaki denklemde.
$$\Rightarrow\:v_i=RC\frac{\text{d}v_o}{\text{d}t}+LC\frac{\text{d}^2v_o}{\text{d}t^2}+v_o$$
$$\Rightarrow\frac{\text{d}^2v_o}{\text{d}t^2}+\left ( \frac{R}{L} \right )\frac{\text{d}v_o}{\text{d}t}+\left ( \frac{1}{LC} \right )v_o=\left ( \frac{1}{LC} \right )v_i$$
Yukarıdaki denklem ikinci dereceden differential equation.
Transfer Fonksiyonu Modeli
Transfer fonksiyonu modeli, kontrol sistemlerinin s-alanı matematiksel bir modelidir. Transfer function Doğrusal Zamanla Değişmeyen (LTI) sistemin, tüm başlangıç koşullarının sıfır olduğu varsayılarak, çıkışın Laplace dönüşümü ile girdinin Laplace dönüşümünün oranı olarak tanımlanır.
Eğer $x(t)$ ve $y(t)$ bir LTI sisteminin girdisi ve çıktısı ise, karşılık gelen Laplace dönüşümleri $X(s)$ ve $Y(s)$.
Bu nedenle, LTI sisteminin transfer fonksiyonu oranına eşittir. $Y(s)$ ve $X(s)$.
$$i.e.,\: Transfer\: Function =\frac{Y(s)}{X(s)}$$
Bir LTI sisteminin transfer fonksiyonu modeli aşağıdaki şekilde gösterilmektedir.

Burada, içinde transfer işlevi olan bir bloğu olan bir LTI sistemini temsil ettik. Ve bu bloğun bir girişi var$X(s)$ & çıktı $Y(s)$.
Misal
Daha önce, bir elektrik sisteminin diferansiyel denklemini şu şekilde aldık:
$$\frac{\text{d}^2v_o}{\text{d}t^2}+\left ( \frac{R}{L} \right )\frac{\text{d}v_o}{\text{d}t}+\left ( \frac{1}{LC} \right )v_o=\left ( \frac{1}{LC} \right )v_i$$
Her iki tarafa da Laplace dönüşümü uygulayın.
$$s^2V_o(s)+\left ( \frac{sR}{L} \right )V_o(s)+\left ( \frac{1}{LC} \right )V_o(s)=\left ( \frac{1}{LC} \right )V_i(s)$$
$$\Rightarrow \left \{ s^2+\left ( \frac{R}{L} \right )s+\frac{1}{LC} \right \}V_o(s)=\left ( \frac{1}{LC} \right )V_i(s)$$
$$\Rightarrow \frac{V_o(s)}{V_i(s)}=\frac{\frac{1}{LC}}{s^2+\left ( \frac{R}{L} \right )s+\frac{1}{LC}}$$
Nerede,
$v_i(s)$ giriş voltajının Laplace dönüşümüdür $v_i$
$v_o(s)$ çıkış geriliminin Laplace dönüşümüdür $v_o$
Yukarıdaki denklem bir transfer functionikinci dereceden elektrik sisteminin. Bu sistemin transfer fonksiyonu modeli aşağıda gösterilmiştir.

Burada, içinde transfer işlevine sahip bir bloğun bulunduğu ikinci dereceden bir elektrik sistemini gösteriyoruz. Ve bu bloğun bir girişi var$V_i(s)$ & bir çıktı $V_o(s)$.
Bu bölümde tartışalım differential equation modelingmekanik sistemlerin. Hareketin türüne göre iki tür mekanik sistem vardır.
- Translasyonel mekanik sistemler
- Rotasyonel mekanik sistemler
Translasyonel Mekanik Sistemlerin Modellenmesi
Translasyonel mekanik sistemler bir straight line. Bu sistemler esas olarak üç temel unsurdan oluşur. Bunlar kütle, yay ve gösterge veya sönümleyicidir.
Öteleme mekanik bir sisteme bir kuvvet uygulanırsa, sistemin kütlesi, esnekliği ve sürtünmesi nedeniyle karşıt kuvvetler tarafından karşı çıkar. Uygulanan kuvvet ve karşıt kuvvetler zıt yönlerde olduğundan, sisteme etkiyen kuvvetlerin cebirsel toplamı sıfırdır. Şimdi bu üç unsurun karşı koyduğu kuvveti ayrı ayrı görelim.
kitle
Kütle, depolayan bir bedenin özelliğidir kinetic energy. Kütlesi olan bir cisme kuvvet uygulanırsaM, o zaman kütle nedeniyle karşıt bir kuvvet tarafından karşı çıkar. Bu karşıt kuvvet, vücudun ivmesi ile orantılıdır. Esnekliğin ve sürtünmenin ihmal edilebilir olduğunu varsayın.

$$F_m\propto\: a$$
$$\Rightarrow F_m=Ma=M\frac{\text{d}^2x}{\text{d}t^2}$$
$$F=F_m=M\frac{\text{d}^2x}{\text{d}t^2}$$
Nerede,
F uygulanan kuvvet
Fm kütle nedeniyle karşıt kuvvettir
M kütle
a ivme
x yer değiştirme
İlkbahar
Bahar depolayan bir unsurdur potential energy. Yaya kuvvet uygulanırsaK, o zaman yay esnekliğinden dolayı karşıt bir kuvvetle karşı karşıya gelir. Bu zıt kuvvet, yayın yer değiştirmesiyle orantılıdır. Kütle ve sürtünmenin ihmal edilebilir olduğunu varsayın.

$$F\propto\: x$$
$$\Rightarrow F_k=Kx$$
$$F=F_k=Kx$$
Nerede,
F uygulanan kuvvet
Fk yay esnekliğinden kaynaklanan zıt kuvvettir
K bahar sabiti
x yer değiştirme
Dashpot
Dashpot üzerine bir kuvvet uygulanırsa B, daha sonra karşı bir güç tarafından karşı çıkıyor frictionDashpot'un. Bu zıt kuvvet, cismin hızıyla orantılıdır. Kütle ve esnekliğin ihmal edilebilir olduğunu varsayın.

$$F_b\propto\: \nu$$
$$\Rightarrow F_b=B\nu=B\frac{\text{d}x}{\text{d}t}$$
$$F=F_b=B\frac{\text{d}x}{\text{d}t}$$
Nerede,
Fb Dashpot'un sürtünmesinden kaynaklanan karşıt güçtür
B sürtünme katsayısı
v hız
x yer değiştirme
Rotasyonel Mekanik Sistemlerin Modellenmesi
Rotasyonel mekanik sistemler sabit bir eksen etrafında hareket eder. Bu sistemler esas olarak üç temel unsurdan oluşur. Onlarmoment of inertia, torsional spring ve dashpot.
Dönme mekanik bir sisteme bir tork uygulanırsa, sistemin atalet momenti, esnekliği ve sürtünmesi nedeniyle ters torklarla karşı karşıya kalır. Uygulanan tork ve karşıt torklar zıt yönlerde olduğundan, sisteme etki eden torkların cebirsel toplamı sıfırdır. Şimdi bu üç elementin karşı koyduğu torku ayrı ayrı görelim.
Atalet Momenti
Öteleme mekanik sistemde, kütle kinetik enerjiyi depolar. Benzer şekilde, rotasyonel mekanik sistemde eylemsizlik momenti depolarkinetic energy.
Eylemsizlik momentine sahip bir gövdeye bir tork uygulanırsa J, daha sonra eylemsizlik momenti nedeniyle karşıt bir tork ile karşı karşıya gelir. Bu zıt tork, gövdenin açısal ivmesiyle orantılıdır. Esnekliğin ve sürtünmenin ihmal edilebilir olduğunu varsayın.

$$T_j\propto\: \alpha$$
$$\Rightarrow T_j=J\alpha=J\frac{\text{d}^2\theta}{\text{d}t^2}$$
$$T=T_j=J\frac{\text{d}^2\theta}{\text{d}t^2}$$
Nerede,
T uygulanan torktur
Tj atalet momentinden kaynaklanan zıt torktur
J atalet momentidir
α açısal ivmedir
θ açısal yer değiştirme
Burulma Yayı
Öteleme mekanik sistemde, yay potansiyel enerjiyi depolar. Benzer şekilde, rotasyonel mekanik sistemde burulma yayı depolarpotential energy.
Burulma yayına bir tork uygulanırsa K, daha sonra burulma yayının esnekliği nedeniyle karşıt bir tork ile karşı karşıya gelir. Bu zıt tork, burulma yayının açısal yer değiştirmesi ile orantılıdır. Eylemsizlik ve sürtünme momentinin ihmal edilebilir olduğunu varsayın.
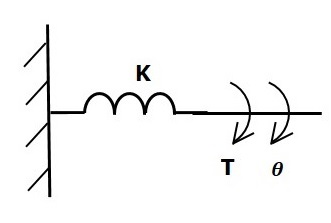
$$T_k\propto\: \theta$$
$$\Rightarrow T_k=K\theta$$
$$T=T_k=K\theta$$
Nerede,
T uygulanan torktur
Tk burulma yayının esnekliğinden kaynaklanan zıt torktur
K burulma yay sabitidir
θ açısal yer değiştirme
Dashpot
Dashpot'a bir tork uygulanırsa B, daha sonra karşı bir torkla karşı çıkıyor rotational frictionDashpot'un. Bu zıt tork, gövdenin açısal hızıyla orantılıdır. Eylemsizlik momentinin ve esnekliğin ihmal edilebilir olduğunu varsayın.
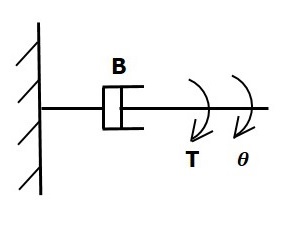
$$T_b\propto\: \omega$$
$$\Rightarrow T_b=B\omega=B\frac{\text{d}\theta}{\text{d}t}$$
$$T=T_b=B\frac{\text{d}\theta}{\text{d}t}$$
Nerede,
Tb gösterge panelinin dönme sürtünmesinden kaynaklanan zıt torktur
B dönme sürtünme katsayısıdır
ω açısal hızdır
θ açısal yer değiştirme
İki sistemin olduğu söyleniyor analogous Aşağıdaki iki koşul karşılanırsa birbirine.
- İki sistem fiziksel olarak farklı
- Bu iki sistemin diferansiyel denklem modellemesi aynıdır
Elektrik sistemleri ve mekanik sistemler fiziksel olarak farklı iki sistemdir. Öteleme mekanik sistemlerin iki tür elektriksel analojisi vardır. Bunlar kuvvet voltajı analojisi ve kuvvet akımı analojisidir.
Kuvvet Gerilimi Analojisi
Kuvvet voltajı analojisinde, matematiksel denklemler translational mechanical system Elektrik sisteminin örgü denklemleri ile karşılaştırılır.
Aşağıdaki şekilde gösterildiği gibi, aşağıdaki translasyonel mekanik sistemi düşünün.
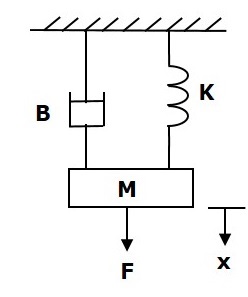
force balanced equation bu sistem için
$$F=F_m+F_b+F_k$$
$\Rightarrow F=M\frac{\text{d}^2x}{\text{d}t^2}+B\frac{\text{d}x}{\text{d}t}+Kx$ (Equation 1)
Aşağıdaki şekilde gösterildiği gibi aşağıdaki elektrik sistemini düşünün. Bu devre bir direnç, bir indüktör ve bir kapasitörden oluşur. Tüm bu elektriksel elemanlar bir seri olarak bağlanmıştır. Bu devreye uygulanan giriş voltajı$V$ volt ve devreden geçen akım $i$ Amper.

Bu devre için örgü denklemi
$V=Ri+L\frac{\text{d}i}{\text{d}t}+\frac{1}{c}\int idt$ (Equation 2)
Vekil, $i=\frac{\text{d}q}{\text{d}t}$ Denklem 2'de.
$$V=R\frac{\text{d}q}{\text{d}t}+L\frac{\text{d}^2q}{\text{d}t^2}+\frac{q}{C}$$
$\Rightarrow V=L\frac{\text{d}^2q}{\text{d}t^2}+R\frac{\text{d}q}{\text{d}t}+\left ( \frac{1}{c} \right )q$ (Equation 3)
Denklem 1 ve Denklem 3'ü karşılaştırarak, öteleme mekanik sistem ve elektrik sisteminin analog miktarlarını elde edeceğiz. Aşağıdaki tablo bu benzer büyüklükleri göstermektedir.
| Öteleme Mekanik Sistem | Elektrik sistemi |
|---|---|
| Kuvvet (F) | Gerilim (V) |
| Kütle (M) | Endüktans (L) |
| Sürtünme Katsayısı (B) | Direnç (R) |
| Yay Sabiti (K) | Kapasitans Karşılıklı $(\frac{1}{c})$ |
| Yer değiştirme (x) | Şarj (q) |
| Hız (v) | Akım (i) |
Benzer şekilde, rotasyonel mekanik sistemler için tork voltajı analojisi vardır. Şimdi bu benzetmeyi tartışalım.
Tork Gerilimi Analojisi
Bu benzetmede, matematiksel denklemler rotational mechanical system Elektrik sisteminin örgü denklemleri ile karşılaştırılır.
Rotasyonel mekanik sistem aşağıdaki şekilde gösterilmektedir.

Tork dengeli denklem
$$T=T_j+T_b+T_k$$
$\Rightarrow T=J\frac{\text{d}^2\theta}{\text{d}t^2}+B\frac{\text{d}\theta}{\text{d}t}+k\theta$ (Equation 4)
Denklem 4 ve Denklem 3'ü karşılaştırarak, döner mekanik sistem ve elektrik sisteminin analog miktarlarını elde edeceğiz. Aşağıdaki tablo bu benzer büyüklükleri göstermektedir.
| Rotasyonel Mekanik Sistem | Elektrik sistemi |
|---|---|
| Tork (T) | Gerilim (V) |
| Atalet Momenti (J) | Endüktans (L) |
| Dönme sürtünme katsayısı (B) | Direnç (R) |
| Burulma yay sabiti (K) | Kapasitans Karşılıklı $(\frac{1}{c})$ |
| Açısal Yer Değiştirme (θ) | Şarj (q) |
| Açısal Hız (ω) | Akım (i) |
Geçerli Analojiyi Zorla
Kuvvet akım analojisinde, matematiksel denklemler translational mechanical system elektrik sisteminin düğüm denklemleri ile karşılaştırılır.
Aşağıdaki şekilde gösterildiği gibi aşağıdaki elektrik sistemini düşünün. Bu devre akım kaynağı, direnç, indüktör ve kapasitörden oluşur. Tüm bu elektriksel elemanlar paralel olarak bağlanmıştır.

Düğüm denklemi
$i=\frac{V}{R}+\frac{1}{L}\int Vdt+C\frac{\text{d}V}{\text{d}t}$ (Equation 5)
Vekil, $V=\frac{\text{d}\Psi}{\text{d}t}$ Denklem 5'te.
$$i=\frac{1}{R}\frac{\text{d}\Psi}{\text{d}t}+\left ( \frac{1}{L} \right )\Psi+C\frac{\text{d}^2\Psi}{\text{d}t^2}$$
$\Rightarrow i=C\frac{\text{d}^2\Psi}{\text{d}t^2}+\left ( \frac{1}{R} \right )\frac{\text{d}\Psi}{\text{d}t}+\left ( \frac{1}{L} \right )\Psi$ (Equation 6)
Denklem 1 ve Denklem 6'yı karşılaştırarak, öteleme mekanik sistem ve elektrik sisteminin analog miktarlarını elde edeceğiz. Aşağıdaki tablo bu benzer büyüklükleri göstermektedir.
| Öteleme Mekanik Sistem | Elektrik sistemi |
|---|---|
| Kuvvet (F) | Akım (i) |
| Kütle (M) | Kapasite (C) |
| Sürtünme katsayısı (B) | Karşılıklı Direniş$(\frac{1}{R})$ |
| Yay sabiti (K) | Endüktans Karşılıklı$(\frac{1}{L})$ |
| Yer değiştirme (x) | Manyetik Akı (ψ) |
| Hız (v) | Gerilim (V) |
Benzer şekilde, rotasyonel mekanik sistemler için bir tork akımı analojisi vardır. Şimdi bu benzetmeyi tartışalım.
Tork Akımı Analojisi
Bu benzetmede, matematiksel denklemler rotational mechanical system elektrik sisteminin düğüm ağ denklemleri ile karşılaştırılır.
Denklem 4 ve Denklem 6'yı karşılaştırarak, benzer miktarlarda döner mekanik sistem ve elektrik sistemi elde edeceğiz. Aşağıdaki tablo bu benzer büyüklükleri göstermektedir.
| Rotasyonel Mekanik Sistem | Elektrik sistemi |
|---|---|
| Tork (T) | Akım (i) |
| Eylemsizlik momenti (J) | Kapasite (C) |
| Dönme sürtünme katsayısı (B) | Karşılıklı Direniş$(\frac{1}{R})$ |
| Burulma yay sabiti (K) | Endüktans Karşılıklı$(\frac{1}{L})$ |
| Açısal yer değiştirme (θ) | Manyetik akı (ψ) |
| Açısal hız (ω) | Gerilim (V) |
Bu bölümde, mekanik sistemlerin elektriksel analojilerini tartıştık. Bu benzetmeler, analog elektrik sisteminden mekanik sistem gibi elektriksel olmayan sistemi incelemek ve analiz etmek için yararlıdır.
Blok diyagramlar tek bir bloktan veya blokların bir kombinasyonundan oluşur. Bunlar, kontrol sistemlerini resimli biçimde temsil etmek için kullanılır.
Blok Diyagramın Temel Öğeleri
Bir blok diyagramın temel öğeleri bir blok, toplama noktası ve kalkış noktasıdır. Bu elemanları tanımlamak için aşağıdaki şekilde gösterildiği gibi bir kapalı döngü kontrol sisteminin blok diyagramını ele alalım.

Yukarıdaki blok diyagram, G (s) ve H (s) transfer fonksiyonlarına sahip iki bloktan oluşur. Aynı zamanda bir toplama noktası ve bir kalkış noktası var. Oklar, sinyallerin akış yönünü gösterir. Şimdi bu unsurları tek tek tartışalım.
Blok
Bir bileşenin transfer fonksiyonu bir blok ile temsil edilir. Blok tek girişli ve tek çıkışlıdır.
Aşağıdaki şekil, giriş X (s), çıkış Y (s) ve transfer fonksiyonu G (s) olan bir bloğu göstermektedir.

Transfer Fonksiyonu,$G(s)=\frac{Y(s)}{X(s)}$
$$\Rightarrow Y(s)=G(s)X(s)$$
Bloğun çıkışı, bloğun transfer fonksiyonunun girdi ile çarpılmasıyla elde edilir.
Toplama Noktası
Toplama noktası, içinde çarpı işareti (X) olan bir daire ile temsil edilir. İki veya daha fazla girişi ve tek çıkışı vardır. Girişlerin cebirsel toplamını üretir. Ayrıca, girişlerin polaritesine bağlı olarak girişlerin toplanması veya çıkarılması veya toplama ve çıkarma kombinasyonunu da gerçekleştirir. Gelin bu üç işlemi tek tek görelim.
Aşağıdaki şekil iki girişli (A, B) ve bir çıkışlı (Y) toplama noktasını göstermektedir. Burada, A ve B girişlerinin pozitif bir işareti vardır. Böylece, toplama noktası Y çıktısını üretir.sum of A and B.
yani, Y = A + B.

Aşağıdaki şekil iki girişli (A, B) ve bir çıkışlı (Y) toplama noktasını göstermektedir. Burada, A ve B girişleri zıt işaretlere sahiptir, yani A pozitif işarete ve B negatif işarete sahiptir. Böylece, toplama noktası çıktıyı üretirY olarak difference of A and B.
Y = A + (-B) = A - B.

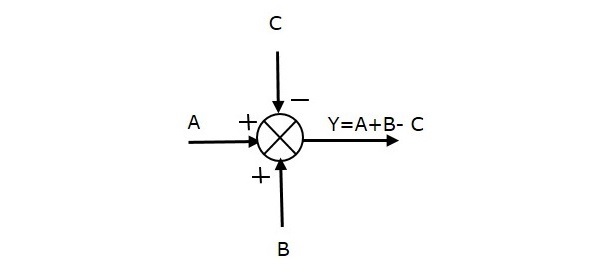
Aşağıdaki şekil, üç giriş (A, B, C) ve bir çıkış (Y) ile toplama noktasını göstermektedir. Burada, A ve B girişleri pozitif işaretlere sahiptir ve C, bir negatif işarete sahiptir. Böylece, toplama noktası çıktıyı üretirY gibi
Y = A + B + (−C) = A + B - C.
Kalkış Noktası
Kalkış noktası, aynı giriş sinyalinin birden fazla daldan geçirilebildiği bir noktadır. Bu, kalkış noktası yardımıyla, aynı girdiyi bir veya daha fazla bloğa, toplama noktalarına uygulayabiliriz.
Aşağıdaki şekilde, kalkış noktası aynı girişi, R (s) iki bloğa daha bağlamak için kullanılır.

Aşağıdaki şekilde, kalkış noktası girişlerden biri olarak C (ler) çıkışını toplama noktasına bağlamak için kullanılır.
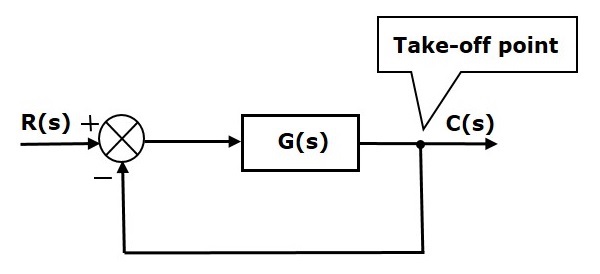
Elektrik Sistemlerinin Blok Şema Gösterimi
Bu bölümde bir elektrik sistemini blok diyagramla gösterelim. Elektrik sistemleri temel olarak üç temel unsur içerir -resistor, inductor and capacitor.
Aşağıdaki şekilde gösterildiği gibi bir dizi RLC devresini düşünün. Burada, V i (t) ve V o (t) giriş ve çıkış voltajlarıdır. Devreden geçen akım ben (t) olsun. Bu devre zaman etki alanı içindedir.

By applying the Laplace transform to this circuit, will get the circuit in s-domain. The circuit is as shown in the following figure.
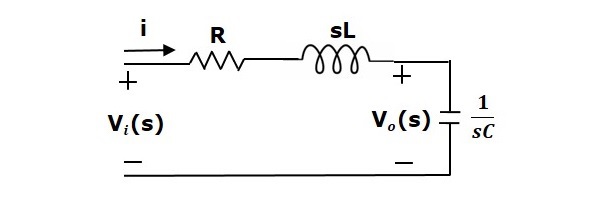
From the above circuit, we can write
$$I(s)=\frac{V_i(s)-V_o(s)}{R+sL}$$
$\Rightarrow I(s)=\left \{ \frac{1}{R+sL} \right \}\left \{ V_i(s)-V_o(s) \right \}$ (Equation 1)
$V_o(s)=\left ( \frac{1}{sC} \right )I(s)$ (Equation 2)
Let us now draw the block diagrams for these two equations individually. And then combine those block diagrams properly in order to get the overall block diagram of series of RLC Circuit (s-domain).
Equation 1 can be implemented with a block having the transfer function, $\frac{1}{R+sL}$. The input and output of this block are $\left \{ V_i(s)-V_o(s) \right \}$ and $I(s)$. We require a summing point to get $\left \{ V_i(s)-V_o(s) \right \}$. The block diagram of Equation 1 is shown in the following figure.

Equation 2 can be implemented with a block having transfer function, $\frac{1}{sC}$. The input and output of this block are $I(s)$ and $V_o(s)$. The block diagram of Equation 2 is shown in the following figure.

The overall block diagram of the series of RLC Circuit (s-domain) is shown in the following figure.

Similarly, you can draw the block diagram of any electrical circuit or system just by following this simple procedure.
Convert the time domain electrical circuit into an s-domain electrical circuit by applying Laplace transform.
Write down the equations for the current passing through all series branch elements and voltage across all shunt branches.
Draw the block diagrams for all the above equations individually.
Combine all these block diagrams properly in order to get the overall block diagram of the electrical circuit (s-domain).
Block diagram algebra is nothing but the algebra involved with the basic elements of the block diagram. This algebra deals with the pictorial representation of algebraic equations.
Basic Connections for Blocks
There are three basic types of connections between two blocks.
Series Connection
Series connection is also called cascade connection. In the following figure, two blocks having transfer functions $G_1(s)$ and $G_2(s)$ are connected in series.

For this combination, we will get the output $Y(s)$ as
$$Y(s)=G_2(s)Z(s)$$
Where, $Z(s)=G_1(s)X(s)$
$$\Rightarrow Y(s)=G_2(s)[G_1(s)X(s)]=G_1(s)G_2(s)X(s)$$
$$\Rightarrow Y(s)=\lbrace G_1(s)G_2(s)\rbrace X(s)$$
Compare this equation with the standard form of the output equation, $Y(s)=G(s)X(s)$. Where, $G(s) = G_1(s)G_2(s)$.
That means we can represent the series connection of two blocks with a single block. The transfer function of this single block is the product of the transfer functions of those two blocks. The equivalent block diagram is shown below.
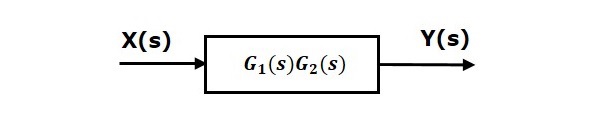
Similarly, you can represent series connection of ‘n’ blocks with a single block. The transfer function of this single block is the product of the transfer functions of all those ‘n’ blocks.
Parallel Connection
The blocks which are connected in parallel will have the same input. In the following figure, two blocks having transfer functions $G_1(s)$ and $G_2(s)$ are connected in parallel. The outputs of these two blocks are connected to the summing point.

For this combination, we will get the output $Y(s)$ as
$$Y(s)=Y_1(s)+Y_2(s)$$
Where, $Y_1(s)=G_1(s)X(s)$ and $Y_2(s)=G_2(s)X(s)$
$$\Rightarrow Y(s)=G_1(s)X(s)+G_2(s)X(s)=\lbrace G_1(s)+G_2(s)\rbrace X(s)$$
Compare this equation with the standard form of the output equation, $Y(s)=G(s)X(s)$.
Where, $G(s)=G_1(s)+G_2(s)$.
That means we can represent the parallel connection of two blocks with a single block. The transfer function of this single block is the sum of the transfer functions of those two blocks. The equivalent block diagram is shown below.

Similarly, you can represent parallel connection of ‘n’ blocks with a single block. The transfer function of this single block is the algebraic sum of the transfer functions of all those ‘n’ blocks.
Feedback Connection
As we discussed in previous chapters, there are two types of feedback — positive feedback and negative feedback. The following figure shows negative feedback control system. Here, two blocks having transfer functions $G(s)$ and $H(s)$ form a closed loop.

The output of the summing point is -
$$E(s)=X(s)-H(s)Y(s)$$
The output $Y(s)$ is -
$$Y(s)=E(s)G(s)$$
Substitute $E(s)$ value in the above equation.
$$Y(s)=\left \{ X(s)-H(s)Y(s)\rbrace G(s) \right\}$$
$$Y(s)\left \{ 1+G(s)H(s)\rbrace = X(s)G(s) \right\}$$
$$\Rightarrow \frac{Y(s)}{X(s)}=\frac{G(s)}{1+G(s)H(s)}$$
Therefore, the negative feedback closed loop transfer function is $\frac{G(s)}{1+G(s)H(s)}$
This means we can represent the negative feedback connection of two blocks with a single block. The transfer function of this single block is the closed loop transfer function of the negative feedback. The equivalent block diagram is shown below.

Similarly, you can represent the positive feedback connection of two blocks with a single block. The transfer function of this single block is the closed loop transfer function of the positive feedback, i.e., $\frac{G(s)}{1-G(s)H(s)}$
Block Diagram Algebra for Summing Points
There are two possibilities of shifting summing points with respect to blocks −
- Shifting summing point after the block
- Shifting summing point before the block
Let us now see what kind of arrangements need to be done in the above two cases one by one.
Shifting Summing Point After the Block
Consider the block diagram shown in the following figure. Here, the summing point is present before the block.

Summing point has two inputs $R(s)$ and $X(s)$. The output of it is $\left \{R(s)+X(s)\right\}$.
So, the input to the block $G(s)$ is $\left \{R(s)+X(s)\right \}$ and the output of it is –
$$Y(s)=G(s)\left \{R(s)+X(s)\right \}$$
$\Rightarrow Y(s)=G(s)R(s)+G(s)X(s)$ (Equation 1)
Now, shift the summing point after the block. This block diagram is shown in the following figure.

Output of the block $G(s)$ is $G(s)R(s)$.
The output of the summing point is
$Y(s)=G(s)R(s)+X(s)$ (Equation 2)
Compare Equation 1 and Equation 2.
The first term $‘G(s) R(s)’$ is same in both the equations. But, there is difference in the second term. In order to get the second term also same, we require one more block $G(s)$. It is having the input $X(s)$ and the output of this block is given as input to summing point instead of $X(s)$. This block diagram is shown in the following figure.
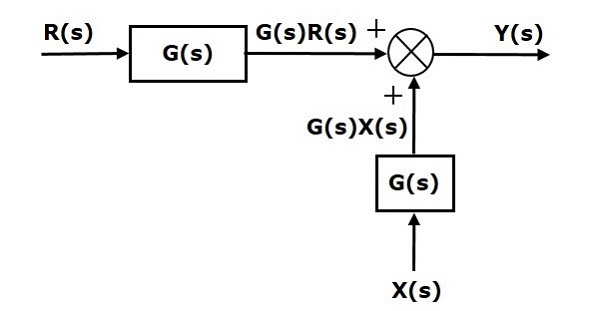
Shifting Summing Point Before the Block
Consider the block diagram shown in the following figure. Here, the summing point is present after the block.

Output of this block diagram is -
$Y(s)=G(s)R(s)+X(s)$ (Equation 3)
Now, shift the summing point before the block. This block diagram is shown in the following figure.

Output of this block diagram is -
$Y(S)=G(s)R(s)+G(s)X(s)$ (Equation 4)
Compare Equation 3 and Equation 4,
The first term $‘G(s) R(s)’$ is same in both equations. But, there is difference in the second term. In order to get the second term also same, we require one more block $\frac{1}{G(s)}$. It is having the input $X(s)$ and the output of this block is given as input to summing point instead of $X(s)$. This block diagram is shown in the following figure.

Block Diagram Algebra for Take-off Points
There are two possibilities of shifting the take-off points with respect to blocks −
- Shifting take-off point after the block
- Shifting take-off point before the block
Let us now see what kind of arrangements are to be done in the above two cases, one by one.
Shifting Take-off Point After the Block
Consider the block diagram shown in the following figure. In this case, the take-off point is present before the block.

Here, $X(s)=R(s)$ and $Y(s)=G(s)R(s)$
When you shift the take-off point after the block, the output $Y(s)$ will be same. But, there is difference in $X(s)$ value. So, in order to get the same $X(s)$ value, we require one more block $\frac{1}{G(s)}$. It is having the input $Y(s)$ and the output is $X(s)$. This block diagram is shown in the following figure.

Shifting Take-off Point Before the Block
Consider the block diagram shown in the following figure. Here, the take-off point is present after the block.

Here, $X(s)=Y(s)=G(s)R(s)$
When you shift the take-off point before the block, the output $Y(s)$ will be same. But, there is difference in $X(s)$ value. So, in order to get same $X(s)$ value, we require one more block $G(s)$. It is having the input $R(s)$ and the output is $X(s)$. This block diagram is shown in the following figure.
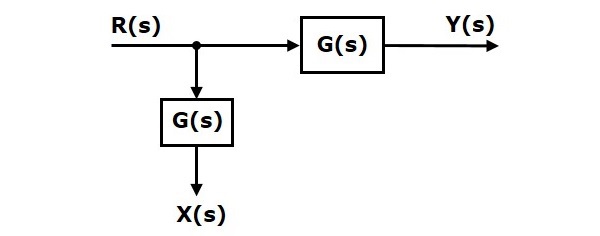
The concepts discussed in the previous chapter are helpful for reducing (simplifying) the block diagrams.
Block Diagram Reduction Rules
Follow these rules for simplifying (reducing) the block diagram, which is having many blocks, summing points and take-off points.
Rule 1 − Check for the blocks connected in series and simplify.
Rule 2 − Check for the blocks connected in parallel and simplify.
Rule 3 − Check for the blocks connected in feedback loop and simplify.
Rule 4 − If there is difficulty with take-off point while simplifying, shift it towards right.
Rule 5 − If there is difficulty with summing point while simplifying, shift it towards left.
Rule 6 − Repeat the above steps till you get the simplified form, i.e., single block.
Note − The transfer function present in this single block is the transfer function of the overall block diagram.
Example
Consider the block diagram shown in the following figure. Let us simplify (reduce) this block diagram using the block diagram reduction rules.

Step 1 − Use Rule 1 for blocks $G_1$ and $G_2$. Use Rule 2 for blocks $G_3$ and $G_4$. The modified block diagram is shown in the following figure.

Step 2 − Use Rule 3 for blocks $G_1G_2$ and $H_1$. Use Rule 4 for shifting take-off point after the block $G_5$. The modified block diagram is shown in the following figure.

Step 3 − Use Rule 1 for blocks $(G_3 + G_4)$ and $G_5$. The modified block diagram is shown in the following figure.

Step 4 − Use Rule 3 for blocks $(G_3 + G_4)G_5$ and $H_3$. The modified block diagram is shown in the following figure.

Step 5 − Use Rule 1 for blocks connected in series. The modified block diagram is shown in the following figure.

Step 6 − Use Rule 3 for blocks connected in feedback loop. The modified block diagram is shown in the following figure. This is the simplified block diagram.
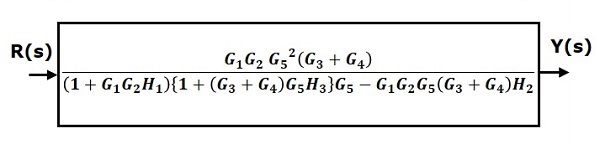
Therefore, the transfer function of the system is
$$\frac{Y(s)}{R(s)}=\frac{G_1G_2G_5^2(G_3+G_4)}{(1+G_1G_2H_1)\lbrace 1+(G_3+G_4)G_5H_3\rbrace G_5-G_1G_2G_5(G_3+G_4)H_2}$$
Note − Follow these steps in order to calculate the transfer function of the block diagram having multiple inputs.
Step 1 − Find the transfer function of block diagram by considering one input at a time and make the remaining inputs as zero.
Step 2 − Repeat step 1 for remaining inputs.
Step 3 − Get the overall transfer function by adding all those transfer functions.
The block diagram reduction process takes more time for complicated systems. Because, we have to draw the (partially simplified) block diagram after each step. So, to overcome this drawback, use signal flow graphs (representation).
In the next two chapters, we will discuss about the concepts related to signal flow graphs, i.e., how to represent signal flow graph from a given block diagram and calculation of transfer function just by using a gain formula without doing any reduction process.
Signal flow graph is a graphical representation of algebraic equations. In this chapter, let us discuss the basic concepts related signal flow graph and also learn how to draw signal flow graphs.
Basic Elements of Signal Flow Graph
Nodes and branches are the basic elements of signal flow graph.
Node
Node is a point which represents either a variable or a signal. There are three types of nodes — input node, output node and mixed node.
Input Node − It is a node, which has only outgoing branches.
Output Node − It is a node, which has only incoming branches.
Mixed Node − It is a node, which has both incoming and outgoing branches.
Example
Let us consider the following signal flow graph to identify these nodes.

The nodes present in this signal flow graph are y1, y2, y3 and y4.
y1 and y4 are the input node and output node respectively.
y2 and y3 are mixed nodes.
Branch
Branch is a line segment which joins two nodes. It has both gain and direction. For example, there are four branches in the above signal flow graph. These branches have gains of a, b, c and -d.
Construction of Signal Flow Graph
Let us construct a signal flow graph by considering the following algebraic equations −
$$y_2=a_{12}y_1+a_{42}y_4$$
$$y_3=a_{23}y_2+a_{53}y_5$$
$$y_4=a_{34}y_3$$
$$y_5=a_{45}y_4+a_{35}y_3$$
$$y_6=a_{56}y_5$$
There will be six nodes (y1, y2, y3, y4, y5 and y6) and eight branches in this signal flow graph. The gains of the branches are a12, a23, a34, a45, a56, a42, a53 and a35.
To get the overall signal flow graph, draw the signal flow graph for each equation, then combine all these signal flow graphs and then follow the steps given below −
Step 1 − Signal flow graph for $y_2 = a_{13}y_1 + a_{42}y_4$ is shown in the following figure.

Step 2 − Signal flow graph for $y_3 = a_{23}y_2 + a_{53}y_5$ is shown in the following figure.

Step 3 − Signal flow graph for $y_4 = a_{34}y_3$ is shown in the following figure.

Step 4 − Signal flow graph for $y_5 = a_{45}y_4 + a_{35}y_3$ is shown in the following figure.

Step 5 − Signal flow graph for $y_6 = a_{56}y_5$ is shown in the following figure.

Step 6 − Signal flow graph of overall system is shown in the following figure.

Conversion of Block Diagrams into Signal Flow Graphs
Follow these steps for converting a block diagram into its equivalent signal flow graph.
Represent all the signals, variables, summing points and take-off points of block diagram as nodes in signal flow graph.
Represent the blocks of block diagram as branches in signal flow graph.
Represent the transfer functions inside the blocks of block diagram as gains of the branches in signal flow graph.
Connect the nodes as per the block diagram. If there is connection between two nodes (but there is no block in between), then represent the gain of the branch as one. For example, between summing points, between summing point and takeoff point, between input and summing point, between take-off point and output.
Misal
Aşağıdaki blok diyagramı eşdeğer sinyal akış grafiğine çevirelim.

Giriş sinyalini temsil edin $R(s)$ ve çıkış sinyali $C(s)$ giriş düğümü olarak blok diyagramının $R(s)$ ve çıkış düğümü $C(s)$ sinyal akış grafiği.
Sadece referans için, kalan düğümler (y 1 ila y 9 ) blok diyagramda etiketlenmiştir. Giriş ve çıkış düğümleri dışında dokuz düğüm vardır. Bu, dört toplama noktası için dört düğüm, dört kalkış noktası için dört düğüm ve bloklar arasındaki değişken için bir düğümdür$G_1$ ve $G_2$.
Aşağıdaki şekil eşdeğer sinyal akış grafiğini göstermektedir.

Mason'un kazanç formülü yardımıyla (sonraki bölümde tartışılmıştır), bu sinyal akış grafiğinin transfer fonksiyonunu hesaplayabilirsiniz. Bu, sinyal akış grafiklerinin avantajıdır. Burada, transfer fonksiyonunu hesaplamak için sinyal akış grafiklerini basitleştirmemize (azaltmamıza) gerek yoktur.
Şimdi Mason Kazanç Formülünü tartışalım. Bir sinyal akış grafiğinde 'N' ileri yol olduğunu varsayalım. Bir sinyal akış grafiğinin giriş ve çıkış düğümleri arasındaki kazanç,transfer functionsistemin. Mason'un kazanç formülü kullanılarak hesaplanabilir.
Mason’s gain formula is
$$T=\frac{C(s)}{R(s)}=\frac{\Sigma ^N _{i=1}P_i\Delta _i}{\Delta}$$
Nerede,
C(s) çıktı düğümü
R(s) giriş düğümü
T transfer işlevi mi yoksa kazanç mı $R(s)$ ve $C(s)$
Pii inci ileri yol kazancı
$\Delta =1-(sum \: of \: all \: individual \: loop \: gains)$
$+(sum \: of \: gain \: products \: of \: all \: possible \: two \:nontouching \: loops)$
$$-(sum \: of \: gain \: products \: of \: all \: possible \: three \: nontouching \: loops)+...$$
Δ i i dokunmadan ilmekleri kaldırarak Ô elde edilen inci ileri yolu .
Burada yer alan temel terminolojiyi anlamak için aşağıdaki sinyal akış grafiğini düşünün.

Yol
Dalların bir düğümden diğer herhangi bir düğüme, dal okları yönünde çapraz geçişidir. Herhangi bir düğümü birden fazla geçmemelidir.
Examples - $y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5$ ve $y_5 \rightarrow y_3 \rightarrow y_2$
İleri Yol
Giriş düğümünden çıkış düğümüne var olan yol, forward path.
Examples - $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_6$ ve $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_5 \rightarrow y_6$.
İleri Yol Kazanımı
İleri yolun tüm branş kazançlarının çarpımı hesaplanarak elde edilir.
Examples - $abcde$ ileriye doğru yol kazancı $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_6$ ve abge ileriye doğru yol kazancıdır $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_5 \rightarrow y_6$.
Döngü
Bir düğümden başlayıp aynı düğümde biten yol, loop. Dolayısıyla kapalı bir yoldur.
Examples - $y_2 \rightarrow y_3 \rightarrow y_2$ ve $y_3 \rightarrow y_5 \rightarrow y_3$.
Döngü Kazancı
Bir döngünün tüm dal kazanımlarının çarpımı hesaplanarak elde edilir.
Examples - $b_j$ döngü kazancı $y_2 \rightarrow y_3 \rightarrow y_2$ ve $g_h$ döngü kazancı $y_3 \rightarrow y_5 \rightarrow y_3$.
Dokunmadan Döngüler
Bunlar, herhangi bir ortak düğüme sahip olmaması gereken döngülerdir.
Examples - Döngüler, $y_2 \rightarrow y_3 \rightarrow y_2$ ve $y_4 \rightarrow y_5 \rightarrow y_4$ dokunmuyor.
Mason Kazanç Formülü Kullanılarak Transfer Fonksiyonunun Hesaplanması
Transfer fonksiyonunu bulmak için aynı sinyal akış grafiğini ele alalım.

İleri yol sayısı, N = 2.
İlk ileriye doğru yol - $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_6$.
İlk ileri yol kazancı, $p_1 = abcde$.
İkinci ileri yol - $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_5 \rightarrow y_6$.
İkinci ileri yol kazancı, $p_2 = abge$.
Bireysel döngü sayısı, L = 5.
Döngüler - $y_2 \rightarrow y_3 \rightarrow y_2$, $y_3 \rightarrow y_5 \rightarrow y_3$, $y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_3$, $y_4 \rightarrow y_5 \rightarrow y_4$ ve $y_5 \rightarrow y_5$.
Döngü kazançları - $l_1 = bj$, $l_2 = gh$, $l_3 = cdh$, $l_4 = di$ ve $l_5 = f$.
İki dokunmasız döngü sayısı = 2.
İlk dokunmayan döngüler çifti - $y_2 \rightarrow y_3 \rightarrow y_2$, $y_4 \rightarrow y_5 \rightarrow y_4$.
İlk dokunmayan döngü çiftinin ürününü kazanın, $l_1l_4 = bjdi$
İkinci dokunmasız döngü çifti - $y_2 \rightarrow y_3 \rightarrow y_2$, $y_5 \rightarrow y_5$.
İkinci dokunmasız döngü çiftinin çarpımı - $l_1l_5 = bjf$
Bu sinyal akış grafiğinde daha fazla sayıda (ikiden fazla) dokunmasız döngü mevcut değildir.
Biliyoruz,
$\Delta =1-(sum \: of \: all \: individual \: loop \: gains)$
$+(sum \: of \: gain \: products \: of \: all \: possible \: two \:nontouching \: loops)$
$$-(sum \: of \: gain \: products \: of \: all \: possible \: three \: nontouching \: loops)+...$$
Yukarıdaki denklemdeki değerleri değiştirin,
$\Delta =1-(bj+gh+cdh+di+f)+(bjdi+bjf)-(0)$
$\Rightarrow \Delta=1-(bj+gh+cdh+di+f)+bjdi+bjf$
İlk ileri yola temas etmeyen bir döngü yoktur.
Yani, $\Delta_1=1$.
Benzer şekilde, $\Delta_2=1$. Çünkü, ikinci ileri yola temas etmeyen döngü yok.
İkame, Mason'un kazanç formülünde N = 2
$$T=\frac{C(s)}{R(s)}=\frac{\Sigma ^2 _{i=1}P_i\Delta _i}{\Delta}$$
$$T=\frac{C(s)}{R(s)}=\frac{P_1\Delta_1+P_2\Delta_2}{\Delta}$$
Yukarıdaki denklemdeki tüm gerekli değerleri değiştirin.
$$T=\frac{C(s)}{R(s)}=\frac{(abcde)1+(abge)1}{1-(bj+gh+cdh+di+f)+bjdi+bjf}$$
$$\Rightarrow T=\frac{C(s)}{R(s)}=\frac{(abcde)+(abge)}{1-(bj+gh+cdh+di+f)+bjdi+bjf}$$
Bu nedenle, transfer işlevi -
$$T=\frac{C(s)}{R(s)}=\frac{(abcde)+(abge)}{1-(bj+gh+cdh+di+f)+bjdi+bjf}$$
Kontrol sistemlerinin tepkisini hem zaman alanında hem de frekans alanında analiz edebiliriz. Daha sonraki bölümlerde kontrol sistemlerinin frekans yanıt analizini tartışacağız. Şimdi kontrol sistemlerinin zaman yanıt analizini tartışalım.
Zaman Tepkisi nedir?
Bir giriş için kontrol sisteminin çıkışı zamana göre değişiklik gösteriyorsa, buna time responsekontrol sisteminin. Zaman cevabı iki bölümden oluşur.
- Geçici tepki
- Kararlı durum yanıtı
Kontrol sisteminin zaman alanındaki tepkisi aşağıdaki şekilde gösterilmiştir.

Burada hem geçici hem de sabit durumlar şekilde gösterilmektedir. Bu durumlara karşılık gelen yanıtlar, geçici ve sabit durum yanıtları olarak bilinir.
Matematiksel olarak, c (t) zaman yanıtını şu şekilde yazabiliriz:
$$c(t)=c_{tr}(t)+c_{ss}(t)$$
Nerede,
- c tr (t) geçici yanıttır
- c ss (t) kararlı durum cevabıdır
Geçici tepki
Kontrol sistemine girdi uyguladıktan sonra, çıkışın kararlı duruma ulaşması belirli bir zaman alır. Böylece, sabit bir duruma geçene kadar çıkış geçici durumda olacaktır. Bu nedenle, geçici durum sırasında kontrol sisteminin tepkisi olarak bilinirtransient response.
Büyük 't' değerleri için geçici yanıt sıfır olacaktır. İdeal olarak, bu 't' değeri sonsuzdur ve pratikte beş kat sabittir.
Matematiksel olarak şöyle yazabiliriz
$$\lim_{t\rightarrow \infty }c_{tr}(t)=0$$
Kararlı durum tepkisi
Büyük 't' değerleri için geçici yanıt sıfır değerine sahip olduktan sonra bile kalan zaman yanıtının parçası olarak bilinir steady state response. Bu, geçici yanıtın sabit durumda bile sıfır olacağı anlamına gelir.
Example
Kontrol sisteminin zaman cevabının geçici ve sabit durum terimlerini bulalım $c(t)=10+5e^{-t}$
İşte ikinci dönem $5e^{-t}$ sıfır olacak tsonsuzluğu ifade eder. Yani, butransient term. Ve ilk 10 terim şu şekilde kalır:tsonsuza yaklaşır. Yani, busteady state term.
Standart Test Sinyalleri
Standart test sinyalleri impuls, adım, rampa ve paraboliktir. Bu sinyaller, çıkışın zaman yanıtını kullanarak kontrol sistemlerinin performansını bilmek için kullanılır.
Birim Darbe Sinyali
Bir birim dürtü sinyali, δ (t) olarak tanımlanır
$\delta (t)=0$ için $t\neq 0$
ve $\int_{0^-}^{0^+} \delta (t)dt=1$
Aşağıdaki şekil birim darbe sinyalini göstermektedir.

Dolayısıyla, birim dürtü sinyali yalnızca 't' sıfıra eşit olduğunda mevcuttur. Bu sinyalin alanı 't' etrafındaki küçük bir zaman aralığında sıfıra eşittir birdir. Birim dürtü sinyalinin değeri, diğer tüm 't' değerleri için sıfırdır.
Birim Adım Sinyali
Bir birim adım sinyali, u (t) olarak tanımlanır
$$u(t)=1;t\geq 0$$
$=0; t<0$
Aşağıdaki şekil birim adım sinyalini göstermektedir.

Dolayısıyla, sıfır dahil tüm pozitif 't' değerleri için birim adım sinyali mevcuttur. Ve değeri bu aralıkta birdir. Birim adım sinyalinin değeri, "t" nin tüm negatif değerleri için sıfırdır.
Birim Rampa Sinyali
Bir birim rampa sinyali, r (t) şu şekilde tanımlanır:
$$r(t)=t; t\geq 0$$
$=0; t<0$
Birim rampa sinyali yazabiliriz, $r(t)$ birim adım sinyali açısından, $u(t)$ gibi
$$r(t)=tu(t)$$
Aşağıdaki şekil birim rampa sinyalini göstermektedir.

Bu nedenle, sıfır dahil tüm pozitif 't' değerleri için birim rampa sinyali mevcuttur. Ve değeri bu aralıkta 't'ye göre doğrusal olarak artar. Birim rampa sinyalinin değeri, 't'nin tüm negatif değerleri için sıfırdır.
Birim Parabolik Sinyal
Bir birim parabolik sinyal, p (t) şu şekilde tanımlanır:
$$p(t)=\frac{t^2}{2}; t\geq 0$$
$=0; t<0$
Birim parabolik sinyal yazabiliriz, $p(t)$ birim adım sinyali açısından, $u(t)$ gibi,
$$p(t)=\frac{t^2}{2}u(t)$$
Aşağıdaki şekil birim parabolik sinyali gösterir.
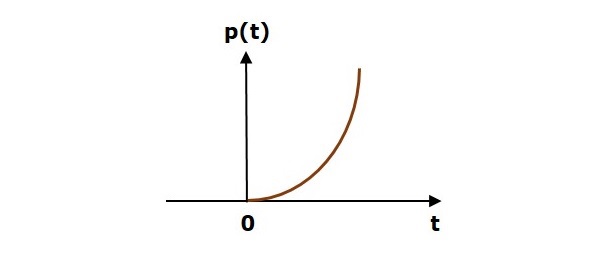
Bu nedenle, birim parabolik sinyalin tüm pozitif değerleri için mevcuttur. ‘t’sıfır dahil. Ve değeri bu aralıkta 't'ye göre doğrusal olmayan bir şekilde artar. Birim parabolik sinyalin değeri, "t" nin tüm negatif değerleri için sıfırdır.
Bu bölümde, birinci dereceden sistemin zaman cevabını tartışalım. Kapalı döngü kontrol sisteminin aşağıdaki blok şemasını düşünün. Burada bir açık döngü transfer fonksiyonu,$\frac{1}{sT}$ birlik olumsuz bir geri bildirim ile bağlantılıdır.

Kapalı döngü kontrol sisteminin transfer fonksiyonunun birlik negatif geri beslemesine sahip olduğunu biliyoruz.
$$\frac{C(s)}{R(s)}=\frac{G(s)}{1+G(s)}$$
Vekil, $G(s)=\frac{1}{sT}$ yukarıdaki denklemde.
$$\frac{C(s)}{R(s)}=\frac{\frac{1}{sT}}{1+\frac{1}{sT}}=\frac{1}{sT+1}$$
S'nin gücü payda teriminde birdir. Bu nedenle, yukarıdaki transfer işlevi birinci derecededir ve sistemin,first order system.
Yukarıdaki denklemi şu şekilde yeniden yazabiliriz:
$$C(s)=\left ( \frac{1}{sT+1} \right )R(s)$$
Nerede,
C(s) c (t) çıkış sinyalinin Laplace dönüşümüdür,
R(s) r (t) giriş sinyalinin Laplace dönüşümüdür ve
T zaman sabiti.
Zaman alanındaki birinci dereceden sistemin yanıtını (çıktı) almak için bu adımları izleyin.
Giriş sinyalinin Laplace dönüşümünü alın $r(t)$.
Denklemi düşünün, $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$
Vekil $R(s)$ Yukarıdaki denklemdeki değer.
Kısmi kesirleri yapın $C(s)$ Eğer istenirse.
Ters Laplace dönüşümü uygula $C(s)$.
Önceki bölümde impuls, adım, rampa ve parabolik gibi standart test sinyallerini gördük. Şimdi her girdi için birinci dereceden sistemin yanıtlarını tek tek bulalım. Yanıtın adı, giriş sinyalinin adına göre verilir. Örneğin, sistemin bir dürtü girişi için tepkisine dürtü yanıtı denir.
Birinci Derece Sistemin Dürtü Tepkisi
Yi hesaba kat unit impulse signal birinci dereceden sisteme girdi olarak.
Yani, $r(t)=\delta (t)$
Her iki tarafa da Laplace dönüşümü uygulayın.
$R(s)=1$
Denklemi düşünün, $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$
Vekil, $R(s) = 1$ yukarıdaki denklemde.
$$C(s)=\left ( \frac{1}{sT+1} \right )(1)=\frac{1}{sT+1}$$
Yukarıdaki denklemi, Laplace dönüşümlerinin standart formlarından birinde yeniden düzenleyin.
$$C(s)=\frac{1}{T\left (\ s+\frac{1}{T} \right )} \Rightarrow C(s)=\frac{1}{T}\left ( \frac{1}{s+\frac{1}{T}} \right )$$
Her iki tarafta ters Laplace dönüşümü uygulayın.
$$c(t)=\frac{1}{T}e^\left ( {-\frac{t}{T}} \right )u(t)$$
Birim dürtü tepkisi aşağıdaki şekilde gösterilmektedir.
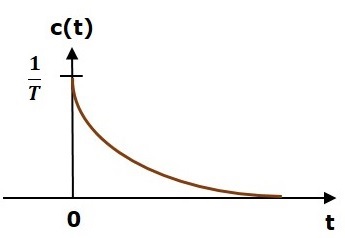
unit impulse responsec (t), pozitif "t" değerleri için üstel bir zayıflama sinyalidir ve "t" nin negatif değerleri için sıfırdır.
Birinci Derece Sistemin Adım Tepkisi
Yi hesaba kat unit step signal birinci dereceden sisteme girdi olarak.
Yani, $r(t)=u(t)$
Her iki tarafa da Laplace dönüşümü uygulayın.
$$R(s)=\frac{1}{s}$$
Denklemi düşünün, $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$
Vekil, $R(s)=\frac{1}{s}$ yukarıdaki denklemde.
$$C(s)=\left ( \frac{1}{sT+1} \right )\left ( \frac{1}{s} \right )=\frac{1}{s\left ( sT+1 \right )}$$
C (ler) 'in kısmi kesirlerini yapın.
$$C(s)=\frac{1}{s\left ( sT+1 \right )}=\frac{A}{s}+\frac{B}{sT+1}$$
$$\Rightarrow \frac{1}{s\left ( sT+1 \right )}=\frac{A\left ( sT+1 \right )+Bs}{s\left ( sT+1 \right )}$$
Her iki tarafta da payda terimi aynıdır. Böylece birbirleri tarafından iptal edilecekler. Bu nedenle, pay terimlerini eşitleyin.
$$1=A\left ( sT+1 \right )+Bs$$
Her iki taraftaki sabit terimleri eşitleyerek, A = 1 elde edersiniz.
İkame, A = 1 ve katsayısını eşitleyin s her iki taraftaki terimler.
$$0=T+B \Rightarrow B=-T$$
İkame, A = 1 ve B = −T'nin kısmi kesir açılımında $C(s)$.
$$C(s)=\frac{1}{s}-\frac{T}{sT+1}=\frac{1}{s}-\frac{T}{T\left ( s+\frac{1}{T} \right )}$$
$$\Rightarrow C(s)=\frac{1}{s}-\frac{1}{s+\frac{1}{T}}$$
Her iki tarafa da ters Laplace dönüşümü uygulayın.
$$c(t)=\left ( 1-e^{-\left ( \frac{t}{T} \right )} \right )u(t)$$
unit step responsec (t) hem geçici hem de sabit durum terimlerine sahiptir.
Birim adım yanıtındaki geçici terim -
$$c_{tr}(t)=-e^{-\left ( \frac{t}{T} \right )}u(t)$$
Birim adım yanıtındaki kararlı durum terimi -
$$c_{ss}(t)=u(t)$$
Aşağıdaki şekil birim adım yanıtını göstermektedir.

Değeri unit step response, c(t)t = 0'da sıfırdır ve t'nin tüm negatif değerleri için. Sıfır değerinden kademeli olarak artmakta ve nihayet kararlı durumda bire ulaşmaktadır. Dolayısıyla, kararlı durum değeri, girişin büyüklüğüne bağlıdır.
Birinci Derece Sistemin Rampa Tepkisi
Yi hesaba kat unit ramp signal birinci dereceden sisteme girdi olarak.
$So, r(t)=tu(t)$
Her iki tarafa da Laplace dönüşümü uygulayın.
$$R(s)=\frac{1}{s^2}$$
Denklemi düşünün, $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$
Vekil, $R(s)=\frac{1}{s^2}$ yukarıdaki denklemde.
$$C(s)=\left ( \frac{1}{sT+1} \right )\left ( \frac{1}{s^2} \right )=\frac{1}{s^2(sT+1)}$$
Kısmi kesirleri yapın $C(s)$.
$$C(s)=\frac{1}{s^2(sT+1)}=\frac{A}{s^2}+\frac{B}{s}+\frac{C}{sT+1}$$
$$\Rightarrow \frac{1}{s^2(sT+1)}=\frac{A(sT+1)+Bs(sT+1)+Cs^2}{s^2(sT+1)}$$
Her iki tarafta da payda terimi aynıdır. Böylece birbirleri tarafından iptal edilecekler. Bu nedenle, pay terimlerini eşitleyin.
$$1=A(sT+1)+Bs(sT+1)+Cs^2$$
Her iki taraftaki sabit terimleri eşitleyerek, A = 1 elde edersiniz.
Değiştirin, A = 1 ve her iki taraftaki s terimlerinin katsayısını eşitleyin.
$$0=T+B \Rightarrow B=-T$$
Benzer şekilde, B = −T yerine koyun ve katsayısını eşitleyin $s^2$her iki taraftaki terimler. Alacaksın$C=T^2$.
A = 1, B = −T ve $C = T^2$ kısmi kesir genişlemesinde $C(s)$.
$$C(s)=\frac{1}{s^2}-\frac{T}{s}+\frac{T^2}{sT+1}=\frac{1}{s^2}-\frac{T}{s}+\frac{T^2}{T\left ( s+\frac{1}{T} \right )}$$
$$\Rightarrow C(s)=\frac{1}{s^2}-\frac{T}{s}+\frac{T}{s+\frac{1}{T}}$$
Her iki tarafa da ters Laplace dönüşümü uygulayın.
$$c(t)=\left ( t-T+Te^{-\left ( \frac{t}{T} \right )} \right )u(t)$$
unit ramp responsec (t) hem geçici hem de sabit durum terimlerine sahiptir.
Birim rampa yanıtındaki geçici terim -
$$c_{tr}(t)=Te^{-\left ( \frac{t}{T} \right )}u(t)$$
Birim rampa yanıtındaki kararlı durum terimi -
$$c_{ss}(t)=(t-T)u(t)$$
Aşağıdaki şekil birim rampa tepkisini göstermektedir.

unit ramp response, c (t), t'nin tüm pozitif değerleri için birim rampa giriş sinyalini takip eder. Ancak, giriş sinyalinden T birimlerinde bir sapma var.
Birinci Derece Sistemin Parabolik Tepkisi
Yi hesaba kat unit parabolic signal birinci dereceden sisteme girdi olarak.
Yani, $r(t)=\frac{t^2}{2}u(t)$
Her iki tarafa da Laplace dönüşümü uygulayın.
$$R(s)=\frac{1}{s^3}$$
Denklemi düşünün, $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$
Vekil $R(s)=\frac{1}{s^3}$ yukarıdaki denklemde.
$$C(s)=\left ( \frac{1}{sT+1} \right )\left( \frac{1}{s^3} \right )=\frac{1}{s^3(sT+1)}$$
Kısmi kesirleri yapın $C(s)$.
$$C(s)=\frac{1}{s^3(sT+1)}=\frac{A}{s^3}+\frac{B}{s^2}+\frac{C}{s}+\frac{D}{sT+1}$$
Sadeleştirdikten sonra, A, B, C ve D değerlerini 1 olarak alacaksınız, $-T, \: T^2\: and \: −T^3$sırasıyla. Bu değerleri, C (s) 'nin yukarıdaki kısmi fraksiyon genişlemesinde ikame edin.
$C(s)=\frac{1}{s^3}-\frac{T}{s^2}+\frac{T^2}{s}-\frac{T^3}{sT+1} \: \Rightarrow C(s)=\frac{1}{s^3}-\frac{T}{s^2}+\frac{T^2}{s}-\frac{T^2}{s+\frac{1}{T}}$
Her iki tarafa da ters Laplace dönüşümü uygulayın.
$$c(t)=\left ( \frac{t^2}{2} -Tt+T^2-T^2e^{-\left ( \frac{t}{T} \right )} \right )u(t)$$
unit parabolic responsec (t) hem geçici hem de sabit durum terimlerine sahiptir.
Birim parabolik yanıttaki geçici terim
$$C_{tr}(t)=-T^2e^{-\left ( \frac{t}{T} \right )}u(t)$$
Birim parabolik yanıttaki kararlı durum terimi,
$$C_{ss}(t)=\left ( \frac{t^2}{2} -Tt+T^2 \right )u(t)$$
Bu yanıtlardan, birinci dereceden kontrol sistemlerinin rampa ve parabolik girdilerle kararlı olmadığı sonucuna varabiliriz çünkü bu yanıtlar sonsuz miktarda bile artmaya devam eder. Birinci dereceden kontrol sistemleri, dürtü ve adım girdileri ile kararlıdır çünkü bu yanıtlar sınırlı çıktıya sahiptir. Ancak, dürtü yanıtının sabit durum terimi yoktur. Bu nedenle, adım sinyali, kontrol sistemlerini yanıtlarından analiz etmek için zaman alanında yaygın olarak kullanılır.
Bu bölümde ikinci mertebe sistemin zaman cevabını tartışalım. Kapalı döngü kontrol sisteminin aşağıdaki blok şemasını düşünün. Burada bir açık döngü transfer fonksiyonu,$\frac{\omega ^2_n}{s(s+2\delta \omega_n)}$ birlik olumsuz bir geri bildirim ile bağlantılıdır.

Kapalı döngü kontrol sisteminin transfer fonksiyonunun birlik negatif geri beslemesine sahip olduğunu biliyoruz.
$$\frac{C(s)}{R(s)}=\frac{G(s)}{1+G(s)}$$
Vekil, $G(s)=\frac{\omega ^2_n}{s(s+2\delta \omega_n)}$ yukarıdaki denklemde.
$$\frac{C(s)}{R(s)}=\frac{\left (\frac{\omega ^2_n}{s(s+2\delta \omega_n)} \right )}{1+ \left ( \frac{\omega ^2_n}{s(s+2\delta \omega_n)} \right )}=\frac{\omega _n^2}{s^2+2\delta \omega _ns+\omega _n^2}$$
Payda teriminde 's' nin gücü ikidir. Bu nedenle, yukarıdaki transfer işlevi ikinci derecededir ve sistemin,second order system.
Karakteristik denklem -
$$s^2+2\delta \omega _ns+\omega _n^2=0$$
Karakteristik denklemin kökleri -
$$s=\frac{-2\omega \delta _n\pm \sqrt{(2\delta\omega _n)^2-4\omega _n^2}}{2}=\frac{-2(\delta\omega _n\pm \omega _n\sqrt{\delta ^2-1})}{2}$$
$$\Rightarrow s=-\delta \omega_n \pm \omega _n\sqrt{\delta ^2-1}$$
- İki kök, δ = 0 olduğunda hayalidir.
- = 1 olduğunda iki kök gerçek ve eşittir.
- İki kök gerçektir ancak δ> 1 olduğunda eşit değildir.
- İki kök, 0 <when <1 olduğunda karmaşık eşleniktir.
Yazabiliriz $C(s)$ denklem olarak,
$$C(s)=\left ( \frac{\omega _n^2}{s^2+2\delta\omega_ns+\omega_n^2} \right )R(s)$$
Nerede,
C(s) çıkış sinyalinin Laplace dönüşümüdür, c (t)
R(s) giriş sinyalinin Laplace dönüşümüdür, r (t)
ωn doğal frekans
δ sönümleme oranıdır.
Zaman alanındaki ikinci dereceden sistemin cevabını (çıktı) almak için bu adımları izleyin.
Giriş sinyalinin Laplace dönüşümünü alın, $r(t)$.
Denklemi düşünün, $C(s)=\left ( \frac{\omega _n^2}{s^2+2\delta\omega_ns+\omega_n^2} \right )R(s)$
Vekil $R(s)$ Yukarıdaki denklemdeki değer.
Kısmi kesirleri yapın $C(s)$ Eğer istenirse.
Ters Laplace dönüşümü uygula $C(s)$.
İkinci Derece Sistemin Adım Tepkisi
Birim adım sinyalini ikinci dereceden sisteme bir giriş olarak düşünün.
Birim adım sinyalinin Laplace dönüşümü,
$$R(s)=\frac{1}{s}$$
İkinci dereceden kapalı döngü kontrol sisteminin transfer fonksiyonunun,
$$\frac{C(s)}{R(s)}=\frac{\omega _n^2}{s^2+2\delta\omega_ns+\omega_n^2}$$
Durum 1: δ = 0
Vekil, $\delta = 0$ transfer fonksiyonunda.
$$\frac{C(s)}{R(s)}=\frac{\omega_n^2}{s^2+\omega_n^2}$$
$$\Rightarrow C(s)=\left( \frac{\omega_n^2}{s^2+\omega_n^2} \right )R(s)$$
Vekil, $R(s) = \frac{1}{s}$ yukarıdaki denklemde.
$$C(s)=\left( \frac{\omega_n^2}{s^2+\omega_n^2} \right )\left( \frac{1}{s} \right )=\frac{\omega_n^2}{s(s^2+\omega_n^2)}$$
Her iki tarafa da ters Laplace dönüşümü uygulayın.
$$c(t)=\left ( 1-\cos(\omega_n t) \right )u(t)$$
Öyleyse, ikinci dereceden sistemin birim adım yanıtı, $/delta = 0$ sabit genlik ve frekansa sahip sürekli bir zaman sinyali olacaktır.
Durum 2: δ = 1
Vekil, $/delta = 1$ transfer fonksiyonunda.
$$\frac{C(s)}{R(s)}=\frac{\omega_n^2}{s^2+2\omega_ns+\omega_n^2}$$
$$\Rightarrow C(s)=\left( \frac{\omega_n^2}{(s+\omega_n)^2} \right)R(s)$$
Vekil, $R(s) = \frac{1}{s}$ yukarıdaki denklemde.
$$C(s)=\left( \frac{\omega_n^2}{(s+\omega_n)^2} \right)\left ( \frac{1}{s} \right)=\frac{\omega_n^2}{s(s+\omega_n)^2}$$
Kısmi kesirleri yapın $C(s)$.
$$C(s)=\frac{\omega_n^2}{s(s+\omega_n)^2}=\frac{A}{s}+\frac{B}{s+\omega_n}+\frac{C}{(s+\omega_n)^2}$$
Sadeleştirdikten sonra, A, B ve C değerlerini şu şekilde alacaksınız: $1,\: -1\: and \: −\omega _n$sırasıyla. Bu değerleri, yukarıdaki kısmi kesir genişlemesinde değiştirin.$C(s)$.
$$C(s)=\frac{1}{s}-\frac{1}{s+\omega_n}-\frac{\omega_n}{(s+\omega_n)^2}$$
Her iki tarafa da ters Laplace dönüşümü uygulayın.
$$c(t)=(1-e^{-\omega_nt}-\omega _nte^{-\omega_nt})u(t)$$
Böylece, ikinci dereceden sistemin birim adım yanıtı, kararlı durumda adım girişine ulaşmaya çalışacaktır.
Durum 3: 0 <δ <1
Transfer fonksiyonunun payda terimini aşağıdaki gibi değiştirebiliriz -
$$s^2+2\delta\omega_ns+\omega_n^2=\left \{ s^2+2(s)(\delta \omega_n)+(\delta \omega_n)^2 \right \}+\omega_n^2-(\delta\omega_n)^2$$
$$=(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)$$
Transfer işlevi olur,
$$\frac{C(s)}{R(s)}=\frac{\omega_n^2}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)}$$
$$\Rightarrow C(s)=\left( \frac{\omega_n^2}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)} \right )R(s)$$
Vekil, $R(s) = \frac{1}{s}$ yukarıdaki denklemde.
$$C(s)=\left( \frac{\omega_n^2}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)} \right )\left( \frac{1}{s} \right )=\frac{\omega_n^2}{s\left ((s+\delta\omega_n)^2+\omega_n^2(1-\delta^2) \right)}$$
Kısmi kesirleri yapın $C(s)$.
$$C(s)=\frac{\omega_n^2}{s\left ((s+\delta\omega_n)^2+\omega_n^2(1-\delta^2) \right)}=\frac{A}{s}+\frac{Bs+C}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)}$$
Sadeleştirdikten sonra, A, B ve C değerlerini şu şekilde alacaksınız: $1,\: -1 \: and \: −2\delta \omega _n$sırasıyla. Bu değerleri, C (s) 'nin yukarıdaki kısmi fraksiyon genişlemesinde ikame edin.
$$C(s)=\frac{1}{s}-\frac{s+2\delta\omega_n}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)}$$
$$C(s)=\frac{1}{s}-\frac{s+\delta\omega_n}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)}-\frac{\delta\omega_n}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)}$$
$C(s)=\frac{1}{s}-\frac{(s+\delta\omega_n)}{(s+\delta\omega_n)^2+(\omega_n\sqrt{1-\delta^2})^2}-\frac{\delta}{\sqrt{1-\delta^2}}\left ( \frac{\omega_n\sqrt{1-\delta^2}}{(s+\delta\omega_n)^2+(\omega_n\sqrt{1-\delta^2})^2} \right )$
Vekil, $\omega_n\sqrt{1-\delta^2}$ gibi $\omega_d$ yukarıdaki denklemde.
$$C(s)=\frac{1}{s}-\frac{(s+\delta\omega_n)}{(s+\delta\omega_n)^2+\omega_d^2}-\frac{\delta}{\sqrt{1-\delta^2}}\left ( \frac{\omega_d}{(s+\delta\omega_n)^2+\omega_d^2} \right )$$
Her iki tarafa da ters Laplace dönüşümü uygulayın.
$$c(t)=\left ( 1-e^{-\delta \omega_nt}\cos(\omega_dt)-\frac{\delta}{\sqrt{1-\delta^2}}e^{-\delta\omega_nt}\sin(\omega_dt) \right )u(t)$$
$$c(t)=\left ( 1-\frac{e^{-\delta\omega_nt}}{\sqrt{1-\delta^2}}\left ( (\sqrt{1-\delta^2})\cos(\omega_dt)+\delta \sin(\omega_dt) \right ) \right )u(t)$$
Eğer $\sqrt{1-\delta^2}=\sin(\theta)$, ardından 'δ' cos (θ) olacaktır. Bu değerleri yukarıdaki denklemde değiştirin.
$$c(t)=\left ( 1-\frac{e^{-\delta\omega_nt}}{\sqrt{1-\delta^2}}(\sin(\theta)\cos(\omega_dt)+\cos(\theta)\sin(\omega_dt)) \right )u(t)$$
$$\Rightarrow c(t)=\left ( 1-\left ( \frac{e^{-\delta\omega_nt}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt+\theta) \right )u(t)$$
Bu nedenle, ikinci derece sistemin birim adım tepkisi, 'δ' sıfır ile bir arasında olduğunda sönümlü salınımlara (azalan genliğe) sahiptir.
Durum 4: δ> 1
Transfer fonksiyonunun payda terimini aşağıdaki gibi değiştirebiliriz -
$$s^2+2\delta\omega_ns+\omega_n^2=\left \{ s^2+2(s)(\delta\omega_n)+(\delta\omega_n)^2 \right \}+\omega_n^2-(\delta\omega_n)^2$$
$$=\left ( s+\delta\omega_n \right )^2-\omega_n^2\left ( \delta^2-1 \right )$$
Transfer işlevi olur,
$$\frac{C(s)}{R(s)}=\frac{\omega_n^2}{(s+\delta\omega_n)^2-\omega_n^2(\delta^2-1)}$$
$$\Rightarrow C(s)=\left ( \frac{\omega_n^2}{(s+\delta\omega_n)^2-\omega_n^2(\delta^2-1)} \right )R(s)$$
Vekil, $R(s) = \frac{1}{s}$ yukarıdaki denklemde.
$C(s)=\left ( \frac{\omega_n^2}{(s+\delta\omega_n)^2-(\omega_n\sqrt{\delta^2-1})^2} \right )\left ( \frac{1}{s} \right )=\frac{\omega_n^2}{s(s+\delta\omega_n+\omega_n\sqrt{\delta^2-1})(s+\delta\omega_n-\omega_n\sqrt{\delta^2-1})}$
Kısmi kesirleri yapın $C(s)$.
$$C(s)=\frac{\omega_n^2}{s(s+\delta\omega_n+\omega_n\sqrt{\delta^2-1})(s+\delta\omega_n-\omega_n\sqrt{\delta^2-1})}$$
$$=\frac{A}{s}+\frac{B}{s+\delta\omega_n+\omega_n\sqrt{\delta^2-1}}+\frac{C}{s+\delta\omega_n-\omega_n\sqrt{\delta^2-1}}$$
Sadeleştirdikten sonra, A, B ve C değerlerini 1 olarak alacaksınız, $\frac{1}{2(\delta+\sqrt{\delta^2-1})(\sqrt{\delta^2-1})}$ ve $\frac{-1}{2(\delta-\sqrt{\delta^2-1})(\sqrt{\delta^2-1})}$sırasıyla. Bu değerleri, yukarıdaki kısmi kesir genişlemesinde değiştirin.$C(s)$.
$$C(s)=\frac{1}{s}+\frac{1}{2(\delta+\sqrt{\delta^2-1})(\sqrt{\delta^2-1})}\left ( \frac{1}{s+\delta\omega_n+\omega_n\sqrt{\delta^2-1}} \right )-\left ( \frac{1}{2(\delta-\sqrt{\delta^2-1})(\sqrt{\delta^2-1})} \right )\left ( \frac{1}{s+\delta\omega_n-\omega_n\sqrt{\delta^2-1}} \right )$$
Her iki tarafa da ters Laplace dönüşümü uygulayın.
$c(t)=\left ( 1+\left ( \frac{1}{2(\delta+\sqrt{\delta^2-1})(\sqrt{\delta^2-1})} \right )e^{-(\delta\omega_n+\omega_n\sqrt{\delta^2-1})t}-\left ( \frac{1}{2(\delta-\sqrt{\delta^2-1})(\sqrt{\delta^2-1})} \right )e^{-(\delta\omega_n-\omega_n\sqrt{\delta^2-1})t} \right )u(t)$
Aşırı sönümlendiğinden, δ> 1 olduğunda ikinci dereceden sistemin birim adım tepkisi, kararlı durumda asla adım girişine ulaşmayacaktır.
İkinci Derece Sistemin Dürtü Tepkisi
impulse response Bu iki yöntemden herhangi biri kullanılarak ikinci dereceden sistemin elde edilmesi mümkündür.
Değerini dikkate alarak adım yanıtını elde ederken ilgili prosedürü izleyin. $R(s)$ yerine 1 olarak $\frac{1}{s}$.
Adım yanıtının farklılaşmasını yapın.
Aşağıdaki tablo, sönümleme oranının 4 durumu için ikinci dereceden sistemin dürtü tepkisini göstermektedir.
| Sönümleme oranının durumu | T ≥ 0 için dürtü yanıtı |
|---|---|
δ = 0 |
$\omega_n\sin(\omega_nt)$ |
δ = 1 |
$\omega_n^2te^{-\omega_nt}$ |
0 <δ <1 |
$\left ( \frac{\omega_ne^{-\delta\omega_nt}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt)$ |
δ> 1 |
$\left ( \frac{\omega_n}{2\sqrt{\delta^2-1}} \right )\left ( e^{-(\delta\omega_n-\omega_n\sqrt{\delta^2-1})t}-e^{-(\delta\omega_n+\omega_n\sqrt{\delta^2-1})t} \right )$ |
Bu bölümde, ikinci dereceden sistemin zaman alanı özelliklerini tartışalım. Düşük sönümlü durum için ikinci derece sistemin adım yanıtı aşağıdaki şekilde gösterilmiştir.

Tüm zaman alanı özellikleri bu şekilde gösterilmektedir. Yerleşme süresine kadar olan tepki geçici tepki olarak bilinir ve yerleşme süresinden sonraki tepki ise sabit durum tepkisi olarak bilinir.
Gecikme süresi
Yanıtın ulaşması için gereken süredir. half of its final valuesıfır andan itibaren. İle gösterilir$t_d$.
'Δ' sıfır ile bir arasında olduğunda, ikinci dereceden sistemin t ≥ 0 için adım yanıtını düşünün.
$$c(t)=1-\left ( \frac{e^{-\delta \omega_nt}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt+\theta)$$
Adım yanıtının son değeri birdir.
Bu nedenle, $t=t_d$, adım yanıtının değeri 0,5 olacaktır. Bu değerleri yukarıdaki denklemde değiştirin.
$$c(t_d)=0.5=1-\left ( \frac{e^{-\delta\omega_nt_d}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt_d+\theta)$$
$$\Rightarrow \left ( \frac{e^{-\delta\omega_nt_d}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt_d+\theta)=0.5$$
Doğrusal yaklaşımı kullanarak, delay time td gibi
$$t_d=\frac{1+0.7\delta}{\omega_n}$$
Yükselme zamanı
Yanıtın yükselmesi için gereken zamandır. 0% to 100% of its final value. Bu,under-damped systems. Aşırı sönümlü sistemler için, süreyi nihai değerin% 10 ila% 90'ı arasında düşünün. Yükselme zamanı ile gösterilirtr.
T = t 1 = 0'da, c (t) = 0.
Adım yanıtının nihai değerinin bir olduğunu biliyoruz.
Bu nedenle, $t = t_2$, adım yanıtının değeri birdir. Bu değerleri aşağıdaki denklemde değiştirin.
$$c(t)=1-\left ( \frac{e^{-\delta \omega_nt}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt+\theta)$$
$$c(t_2)=1=1-\left ( \frac{e^{-\delta\omega_nt_2}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt_2+\theta)$$
$$\Rightarrow \left ( \frac{e^{-\delta\omega_nt_2}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt_2+\theta)=0$$
$$\Rightarrow \sin(\omega_dt_2+\theta)=0$$
$$\Rightarrow \omega_dt_2+\theta=\pi$$
$$\Rightarrow t_2=\frac{\pi-\theta}{\omega_d}$$
Aşağıdaki denklemde t 1 ve t 2 değerlerini değiştirinrise time,
$$t_r=t_2-t_1$$
$$\therefore \: t_r=\frac{\pi-\theta}{\omega_d}$$
Yukarıdaki denklemden yükselme süresinin $t_r$ ve sönümlü frekans $\omega_d$ birbirleriyle ters orantılıdır.
En yoğun zaman
Yanıtın ulaşması için gereken süredir. peak valueilk kez. İle gösterilir$t_p$. Şurada:$t = t_p$cevabın ilk türevi sıfırdır.
Düşük sönümlü durum için ikinci dereceden sistemin adım yanıtının
$$c(t)=1-\left ( \frac{e^{-\delta \omega_nt}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt+\theta)$$
Ayırt etmek $c(t)$ 't'ye göre.
$$\frac{\text{d}c(t)}{\text{d}t}=-\left ( \frac{e^{-\delta\omega_nt}}{\sqrt{1-\delta^2}} \right )\omega_d\cos(\omega_dt+\theta)-\left ( \frac{-\delta\omega_ne^{-\delta\omega_nt}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt+\theta)$$
Vekil, $t=t_p$ ve $\frac{\text{d}c(t)}{\text{d}t}=0$ yukarıdaki denklemde.
$$0=-\left ( \frac{e^{-\delta\omega_nt_p}}{\sqrt{1-\delta^2}} \right )\left [ \omega_d\cos(\omega_dt_p+\theta)-\delta\omega_n\sin(\omega_dt_p+\theta) \right ]$$
$$\Rightarrow \omega_n\sqrt{1-\delta^2}\cos(\omega_dt_p+\theta)-\delta\omega_n\sin(\omega_dt_p+\theta)=0$$
$$\Rightarrow \sqrt{1-\delta^2}\cos(\omega_dt_p+\theta)-\delta\sin(\omega_dt_p+\theta)=0$$
$$\Rightarrow \sin(\theta)\cos(\omega_dt_p+\theta)-\cos(\theta)\sin(\omega_dt_p+\theta)=0$$
$$\Rightarrow \sin(\theta-\omega_dt_p-\theta)=0$$
$$\Rightarrow sin(-\omega_dt_p)=0\Rightarrow -\sin(\omega_dt_p)=0\Rightarrow sin(\omega_dt_p)=0$$
$$\Rightarrow \omega_dt_p=\pi$$
$$\Rightarrow t_p=\frac{\pi}{\omega_d}$$
Yukarıdaki denklemden, en yoğun zamanın $t_p$ ve sönümlü frekans $\omega_d$ birbirleriyle ters orantılıdır.
Tepe Aşımı
Tepe aşımı Mpen yoğun zamanda yanıtın nihai yanıt değerinden sapması olarak tanımlanır. Aynı zamandamaximum overshoot.
Matematiksel olarak şöyle yazabiliriz
$$M_p=c(t_p)-c(\infty)$$
Nerede,
c (t p ), yanıtın tepe değeridir.
c (∞), yanıtın son (sabit durum) değeridir.
Şurada: $t = t_p$, cevap c (t) -
$$c(t_p)=1-\left ( \frac{e^{-\delta\omega_nt_p}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt_p+\theta)$$
Vekil, $t_p=\frac{\pi}{\omega_d}$ yukarıdaki denklemin sağ tarafında.
$$c(t_P)=1-\left ( \frac{e^{-\delta\omega_n\left ( \frac{\pi}{\omega_d} \right )}}{\sqrt{1-\delta^2}} \right )\sin\left ( \omega_d\left ( \frac{\pi}{\omega_d} \right ) +\theta\right )$$
$$\Rightarrow c(t_p)=1-\left ( \frac{e^{-\left ( \frac{\delta\pi}{\sqrt{1-\delta^2}} \right )}}{\sqrt{1-\delta^2}} \right )(-\sin(\theta))$$
Biz biliyoruz ki
$$\sin(\theta)=\sqrt{1-\delta^2}$$
Yani alacağız $c(t_p)$ gibi
$$c(t_p)=1+e^{-\left ( \frac{\delta\pi}{\sqrt{1-\delta^2}} \right )}$$
Değerlerini değiştirin $c(t_p)$ ve $c(\infty)$ zirve aşma denkleminde.
$$M_p=1+e^{-\left ( \frac{\delta\pi}{\sqrt{1-\delta^2}} \right )}-1$$
$$\Rightarrow M_p=e^{-\left ( \frac{\delta\pi}{\sqrt{1-\delta^2}} \right )}$$
Percentage of peak overshoot % $M_p$ bu formül kullanılarak hesaplanabilir.
$$\%M_p=\frac{M_p}{c(\infty )}\times 100\%$$
Değerlerini değiştirerek $M_p$ ve $c(\infty)$ Yukarıdaki formülde, en yüksek aşmanın Yüzdesini alacağız $\%M_p$ gibi
$$\%M_p=\left ( e^ {-\left ( \frac{\delta\pi}{\sqrt{1-\delta^2}} \right )} \right )\times 100\%$$
Yukarıdaki denklemden, tepe aşım yüzdesinin $\% M_p$ sönümleme oranı düşecek $\delta$ artışlar.
Yerleşme zamanı
Yanıtın kararlı duruma ulaşması ve nihai değer etrafında belirtilen tolerans bantları içinde kalması için gereken süredir. Genel olarak tolerans bantları% 2 ve% 5'tir. Yerleşme süresi şu şekilde gösterilir:$t_s$.
% 5 tolerans bandı için yerleşme süresi -
$$t_s=\frac{3}{\delta\omega_n}=3\tau$$
% 2 tolerans bandı için yerleşme süresi -
$$t_s=\frac{4}{\delta\omega_n}=4\tau$$
Nerede, $\tau$ zaman sabiti ve eşittir $\frac{1}{\delta\omega_n}$.
Hem yerleşme zamanı $t_s$ ve zaman sabiti $\tau$ sönümleme oranı ile ters orantılıdır $\delta$.
Hem yerleşme zamanı $t_s$ ve zaman sabiti $\tau$sistem kazancından bağımsızdır. Bu, sistemin bile değişiklik kazandığı anlamına gelir, çökelme süresi$t_s$ ve zaman sabiti $\tau$ asla değişmeyecek.
Misal
Şimdi kapalı döngü transfer fonksiyonuna sahip bir kontrol sisteminin zaman alanı spesifikasyonlarını bulalım. $\frac{4}{s^2+2s+4}$ birim adım sinyali bu kontrol sistemine bir giriş olarak uygulandığında.
İkinci dereceden kapalı döngü kontrol sisteminin transfer fonksiyonunun standart formunun şu şekilde olduğunu biliyoruz.
$$\frac{\omega_n^2}{s^2+2\delta\omega_ns+\omega_n^2}$$
Bu iki transfer fonksiyonunu eşitleyerek, sönümlenmemiş doğal frekansı elde edeceğiz. $\omega_n$ 2 rad / sn ve sönümleme oranı olarak $\delta$ 0.5 olarak.
Sönümlü frekans formülünü biliyoruz $\omega_d$ gibi
$$\omega_d=\omega_n\sqrt{1-\delta^2}$$
Vekil, $\omega_n$ ve $\delta$ yukarıdaki formüldeki değerler.
$$\Rightarrow \omega_d=2\sqrt{1-(0.5)^2}$$
$$\Rightarrow \omega_d=1.732 \: rad/sec$$
Vekil, $\delta$ aşağıdaki ilişkideki değer
$$\theta=\cos^{-1}\delta$$
$$\Rightarrow \theta=\cos^{-1}(0.5)=\frac{\pi}{3}\:rad$$
Verilen transfer fonksiyonu için zaman alanı spesifikasyonlarının değerlerini elde etmek için yukarıdaki gerekli değerleri her bir zaman alanı spesifikasyonunun formülünde değiştirin ve basitleştirin.
Aşağıdaki tablo, zaman alanı spesifikasyonlarının formüllerini, gerekli değerlerin ikamesini ve nihai değerleri göstermektedir.
| Zaman alanı belirtimi | Formül | Formülde değerlerin değiştirilmesi | Nihai değer |
|---|---|---|---|
Gecikme süresi |
$t_d=\frac{1+0.7\delta}{\omega_n}$ |
$t_d=\frac{1+0.7(0.5)}{2}$ |
$t_d$= 0.675 saniye |
Yükselme zamanı |
$t_r=\frac{\pi-\theta}{\omega_d}$ |
$t_r=\frac{\pi-(\frac{\pi}{3})}{1.732}$ |
$t_r$= 1.207 saniye |
En yoğun zaman |
$t_p=\frac{\pi}{\omega_d}$ |
$t_p=\frac{\pi}{1.732}$ |
$t_p$= 1.813 saniye |
% Tepe aşımı |
$\%M_p=\left( e^{-\left (\frac{\delta\pi}{\sqrt{1-\delta^2}} \right ) }\right )\times 100\%$ |
$\%M_p=\left( e^{-\left (\frac{0.5\pi}{\sqrt{1-(0.5)^2}} \right ) }\right )\times 100\%$ |
$\% \: M_p$=% 16,32 |
% 2 tolerans bandı için çökelme süresi |
$t_s=\frac{4}{\delta\omega_n}$ |
$t_S=\frac{4}{(0.5)(2)}$ |
$t_s$= 4 saniye |
Kararlı durum sırasında kontrol sistemi çıktısının istenen tepkiden sapması olarak bilinir. steady state error. Olarak temsil edilir$e_{ss}$. Son değer teoremini kullanarak kararlı durum hatasını aşağıdaki gibi bulabiliriz.
$$e_{ss}=\lim_{t \to \infty}e(t)=\lim_{s \to 0}sE(s)$$
Nerede,
E (s), hata sinyalinin Laplace dönüşümüdür, $e(t)$
Unity feedback ve non-unity feedback kontrol sistemleri için kararlı durum hatalarının nasıl bulunacağını tek tek tartışalım.
Unity Geri Bildirim Sistemleri İçin Kararlı Durum Hataları
Birlik negatif geri beslemesine sahip olan kapalı döngü kontrol sisteminin aşağıdaki blok şemasını düşünün.

Nerede,
- R (s), referans Giriş sinyalinin Laplace dönüşümüdür $r(t)$
- C (s), çıkış sinyalinin Laplace dönüşümüdür $c(t)$
Unity negatif geri besleme kapalı döngü kontrol sisteminin transfer fonksiyonunu biliyoruz.
$$\frac{C(s)}{R(s)}=\frac{G(s)}{1+G(s)}$$
$$\Rightarrow C(s)=\frac{R(s)G(s)}{1+G(s)}$$
Toplama noktasının çıktısı -
$$E(s)=R(s)-C(s)$$
Vekil $C(s)$ Yukarıdaki denklemdeki değer.
$$E(s)=R(s)-\frac{R(s)G(s)}{1+G(s)}$$
$$\Rightarrow E(s)=\frac{R(s)+R(s)G(s)-R(s)G(s)}{1+G(s)}$$
$$\Rightarrow E(s)=\frac{R(s)}{1+G(s)}$$
Vekil $E(s)$ kararlı durum hata formülündeki değer
$$e_{ss}=\lim_{s \to 0} \frac{sR(s)}{1+G(s)}$$
Aşağıdaki tablo, birim adım, birim rampa ve birim parabolik sinyaller gibi standart giriş sinyalleri için kararlı durum hatalarını ve hata sabitlerini gösterir.
| Giriş sinyali | Kararlı durum hatası $e_{ss}$ | Hata sabiti |
|---|---|---|
birim adım sinyali |
$\frac{1}{1+k_p}$ |
$K_p=\lim_{s \to 0}G(s)$ |
birim rampa sinyali |
$\frac{1}{K_v}$ |
$K_v=\lim_{s \to 0}sG(s)$ |
birim parabolik sinyal |
$\frac{1}{K_a}$ |
$K_a=\lim_{s \to 0}s^2G(s)$ |
Nerede, $K_p$, $K_v$ ve $K_a$ sırasıyla konum hatası sabiti, hız hatası sabiti ve ivme hatası sabitidir.
Note - Yukarıdaki giriş sinyallerinden herhangi biri birimden farklı bir genliğe sahipse, karşılık gelen sabit durum hatasını bu genlik ile çarpın.
Note- Birim dürtü sinyali için sabit durum hatasını tanımlayamayız çünkü sadece başlangıç noktasında mevcuttur. Dolayısıyla, dürtü tepkisini birim dürtü girdisiyle şu şekilde karşılaştıramayız:t sonsuzluğu ifade eder.
Misal
Bir giriş sinyali için kararlı durum hatasını bulalım $r(t)=\left( 5+2t+\frac{t^2}{2} \right )u(t)$ negatif geri besleme kontrol sistemi ile birlik $G(s)=\frac{5(s+4)}{s^2(s+1)(s+20)}$
Verilen giriş sinyali, üç sinyal adımı, rampa ve parabolik kombinasyonudur. Aşağıdaki tablo, bu üç sinyal için hata sabitlerini ve kararlı durum hata değerlerini gösterir.
| Giriş sinyali | Hata sabiti | Kararlı durum hatası |
|---|---|---|
$r_1(t)=5u(t)$ |
$K_p=\lim_{s \to 0}G(s)=\infty$ |
$e_{ss1}=\frac{5}{1+k_p}=0$ |
$r_2(t)=2tu(t)$ |
$K_v=\lim_{s \to 0}sG(s)=\infty$ |
$e_{ss2}=\frac{2}{K_v}=0$ |
$r_3(t)=\frac{t^2}{2}u(t)$ |
$K_a=\lim_{s \to 0}s^2G(s)=1$ |
$e_{ss3}=\frac{1}{k_a}=1$ |
Yukarıdaki üç sabit durum hatasını ekleyerek genel kararlı durum hatasını alacağız.
$$e_{ss}=e_{ss1}+e_{ss2}+e_{ss3}$$
$$\Rightarrow e_{ss}=0+0+1=1$$
Bu nedenle, kararlı durum hatası aldık $e_{ss}$ gibi 1 bu örnek için.
Unity Olmayan Geri Bildirim Sistemleri İçin Kararlı Durum Hataları
Bağlantısızlık negatif geri beslemesi olan kapalı döngü kontrol sisteminin aşağıdaki blok şemasını düşünün.

Kararlı durum hatalarını sadece birlik geri besleme sistemleri için bulabiliriz. Bu nedenle, birlik-dışı geribildirim sistemini birlik geri bildirim sistemine dönüştürmeliyiz. Bunun için, yukarıdaki blok şemasına bir adet pozitif geri besleme yolu ve bir adet negatif geri besleme yolu dahil edin. Yeni blok şeması aşağıda gösterildiği gibi görünür.

Birlik negatif geri beslemesini olduğu gibi tutarak yukarıdaki blok diyagramı basitleştirin. Aşağıdaki basitleştirilmiş blok diyagramdır.

Bu blok diyagram, birlik negatif geri beslemeli kapalı döngü kontrol sisteminin blok diyagramına benzer. Burada, tek blok transfer fonksiyonuna sahiptir$\frac{G(s)}{1+G(s)H(s)-G(s)}$ onun yerine $G(s)$. Artık birlik negatif geri besleme sistemleri için verilen kararlı durum hata formülünü kullanarak kararlı durum hatalarını hesaplayabilirsiniz.
Note- Kararsız kapalı döngü sistemler için kararlı durum hatalarını bulmak anlamsızdır. Dolayısıyla, kararlı durum hatalarını sadece kapalı döngü kararlı sistemler için hesaplamamız gerekir. Bu, kararlı durum hatalarını bulmadan önce kontrol sisteminin kararlı olup olmadığını kontrol etmemiz gerektiği anlamına gelir. Bir sonraki bölümde, istikrarla ilgili kavramları tartışacağız.
İstikrar önemli bir kavramdır. Bu bölümde, sistemin kararlılığını ve kararlılığa dayalı sistem türlerini tartışalım.
Kararlılık nedir?
Çıkışı kontrol altındaysa bir sistemin kararlı olduğu söylenir. Aksi takdirde kararsız olduğu söylenir. Birstable system belirli bir sınırlı girdi için sınırlı bir çıktı üretir.
Aşağıdaki şekil kararlı bir sistemin tepkisini göstermektedir.

Bu, birim adım girişi için birinci dereceden kontrol sisteminin tepkisidir. Bu yanıt 0 ile 1 arasında değerlere sahiptir. Yani sınırlı çıktıdır. Birim adım sinyalinin tüm pozitif değerleri için bir değerine sahip olduğunu biliyoruz.tsıfır dahil. Yani, sınırlı bir girdidir. Bu nedenle, birinci dereceden kontrol sistemi, hem girdi hem de çıktı sınırlı olduğu için kararlıdır.
Kararlılığa Dayalı Sistem Türleri
Kararlılığa dayalı sistemleri şu şekilde sınıflandırabiliriz.
- Kesinlikle kararlı sistem
- Koşullu kararlı sistem
- Marjinal olarak kararlı sistem
Kesinlikle Kararlı Sistem
Sistem, tüm sistem bileşeni değerleri aralığında kararlıysa, o zaman absolutely stable system. Açık döngü kontrol sistemi, açık döngü transfer fonksiyonunun tüm kutupları, sol yarısında mevcutsa kesinlikle kararlıdır.‘s’ plane. Benzer şekilde, kapalı döngü transfer fonksiyonunun tüm kutupları 's' düzleminin sol yarısında mevcutsa, kapalı döngü kontrol sistemi kesinlikle kararlıdır.
Koşullu Kararlı Sistem
Sistem, belirli bir sistem bileşeni değerleri aralığı için kararlıysa, o zaman conditionally stable system.
Marjinal Kararlı Sistem
Sistem, sınırlı giriş için sabit genliğe ve sabit salınım frekansına sahip bir çıkış sinyali üreterek kararlıysa, o zaman marginally stable system. Açık döngü kontrol sistemi, sanal eksende açık döngü transfer fonksiyonunun herhangi iki kutbu mevcutsa marjinal olarak kararlıdır. Benzer şekilde, sanal eksende kapalı döngü transfer fonksiyonunun herhangi iki kutbu mevcutsa, kapalı döngü kontrol sistemi marjinal olarak kararlıdır.
Bu bölümde, kararlılık analizini ‘s’alanı RouthHurwitz kararlılık ölçütü kullanılarak. Bu kriterde, kapalı döngü kontrol sistemlerinin kararlılığını bulmak için karakteristik denklemi istiyoruz.
Routh-Hurwitz Kararlılık Kriteri
Routh-Hurwitz kararlılık kriteri, kararlılık için bir gerekli koşula ve bir yeterli koşula sahip olmaktır. Herhangi bir kontrol sistemi gerekli koşulu sağlamazsa kontrol sisteminin kararsız olduğunu söyleyebiliriz. Ancak, kontrol sistemi gerekli koşulu karşılarsa, kararlı olabilir veya olmayabilir. Bu nedenle, yeterli koşul, kontrol sisteminin kararlı olup olmadığını bilmek için yararlıdır.
Routh-Hurwitz Stabilitesi İçin Gerekli Koşul
Gerekli koşul, karakteristik polinomun katsayılarının pozitif olmasıdır. Bu, karakteristik denklemin tüm köklerinin negatif gerçek parçalara sahip olması gerektiği anlamına gelir.
'N' derecesinin karakteristik denklemini düşünün -
$$a_0s^n+a_1s^{n-1}+a_2s^{n-2}+...+a_{n-1}s^1+a_ns^0=0$$
Unutmayın, herhangi bir terim eksik olmamalıdır nthsıra karakteristik denklemi. Bu şu demektirnth sıra karakteristik denkleminin sıfır değerli herhangi bir katsayısı olmamalıdır.
Routh-Hurwitz Stabilitesi için Yeterli Koşul
Yeterli koşul, Routh dizisinin ilk sütunundaki tüm elemanların aynı işarete sahip olmasıdır. Bu, Routh dizisinin ilk sütunundaki tüm öğelerin pozitif veya negatif olması gerektiği anlamına gelir.
Routh Array Yöntemi
Karakteristik denklemin tüm kökleri 's' düzleminin sol yarısında mevcutsa, kontrol sistemi kararlıdır. Karakteristik denklemin en az bir kökü 's' düzleminin sağ yarısında mevcutsa, kontrol sistemi kararsızdır. Bu nedenle, kontrol sisteminin kararlı mı yoksa kararsız mı olduğunu bilmek için karakteristik denklemin köklerini bulmalıyız. Ancak sıra arttıkça karakteristik denklemin köklerini bulmak zordur.
Yani, bu sorunun üstesinden gelmek için orada var Routh array method. Bu yöntemde, karakteristik denklemin köklerinin hesaplanmasına gerek yoktur. Önce Routh tablosunu formüle edin ve Routh tablosunun ilk sütunundaki işaret değişikliklerinin sayısını bulun. Routh tablosunun ilk sütunundaki işaret değişikliklerinin sayısı, 's' düzleminin sağ yarısında bulunan karakteristik denklemin köklerinin sayısını verir ve kontrol sistemi kararsızdır.
Routh masasını oluşturmak için bu prosedürü izleyin.
Routh dizisinin ilk iki satırını aşağıdaki tabloda belirtildiği gibi karakteristik polinomun katsayıları ile doldurun. Katsayısı ile başlayın$s^n$ ve katsayısına kadar devam edin $s^0$.
Routh dizisinin kalan satırlarını aşağıdaki tabloda belirtildiği gibi öğelerle doldurun. İlk sütun elemanını alana kadar bu işleme devam edin.row $s^0$ dır-dir $a_n$. Buraya,$a_n$ katsayısı $s^0$ karakteristik polinomda.
Note - Routh tablosundaki herhangi bir satır elemanının ortak bir faktörü varsa, basitleştirme için satır elemanlarını bu faktörle bölebilirsiniz.
Aşağıdaki tablo, n inci dereceden karakteristik polinomun Routh dizisini göstermektedir .
$$a_0s^n+a_1s^{n-1}+a_2s^{n-2}+...+a_{n-1}s^1+a_ns^0$$
$s^n$ |
$a_0$ |
$a_2$ |
$a_4$ |
$a_6$ |
... |
... |
$s^{n-1}$ |
$a_1$ |
$a_3$ |
$a_5$ |
$a_7$ |
... |
... |
$s^{n-2}$ |
$b_1=\frac{a_1a_2-a_3a_0}{a_1}$ |
$b_2=\frac{a_1a_4-a_5a_0}{a_1}$ |
$b_3=\frac{a_1a_6-a_7a_0}{a_1}$ |
... |
... |
... |
$s^{n-3}$ |
$c_1=\frac{b_1a_3-b_2a_1}{b_1}$ |
$c_2=\frac{b_1a_55-b_3a_1}{b_1}$ |
$\vdots$ |
|||
$\vdots $ |
$\vdots$ |
$\vdots$ |
$\vdots$ |
|||
$s^1$ |
$\vdots$ |
$\vdots$ |
||||
$s^0$ |
$a_n$ |
Example
Karakteristik denklemi olan kontrol sisteminin kararlılığını bulalım,
$$s^4+3s^3+3s^2+2s+1=0$$
Step 1 - Routh-Hurwitz stabilitesi için gerekli koşulu doğrulayın.
Karakteristik polinomun tüm katsayıları, $s^4+3s^3+3s^2+2s+1$olumlu. Böylece kontrol sistemi gerekli koşulu karşılar.
Step 2 - Verilen karakteristik polinom için Routh dizisini oluşturun.
$s^4$ |
$1$ |
$3$ |
$1$ |
$s^3$ |
$3$ |
$2$ |
|
$s^2$ |
$\frac{(3 \times 3)-(2 \times 1)}{3}=\frac{7}{3}$ |
$\frac{(3 \times 1)-(0 \times 1)}{3}=\frac{3}{3}=1$ |
|
$s^1$ |
$\frac{\left ( \frac{7}{3}\times 2 \right )-(1 \times 3)}{\frac{7}{3}}=\frac{5}{7}$ |
||
$s^0$ |
$1$ |
Step 3 - Routh-Hurwitz stabilitesi için yeterli koşulu doğrulayın.
Routh dizisinin ilk sütununun tüm elemanları pozitiftir. Routh dizisinin ilk sütununda işaret değişikliği yoktur. Yani kontrol sistemi kararlı.
Routh Array Özel Durumları
Routh masasını oluştururken iki tür durumla karşılaşabiliriz. Bu iki durumdan Routh tablosunu tamamlamak zordur.
İki özel durum:
- Routh dizisinin herhangi bir satırının ilk elemanı sıfırdır.
- Routh dizisinin herhangi bir satırının tüm elemanları sıfırdır.
Şimdi bu iki durumdaki zorluğun üstesinden nasıl gelineceğini tek tek tartışalım.
Routh dizisinin herhangi bir satırının ilk Elemanı sıfırdır
Routh dizisinin herhangi bir satırı yalnızca ilk öğeyi sıfır olarak içeriyorsa ve kalan öğelerden en az biri sıfır olmayan değere sahipse, ilk öğeyi küçük bir pozitif tamsayı ile değiştirin, $\epsilon$. Ardından Routh masasını tamamlama sürecine devam edin. Şimdi, yerine Routh tablosunun ilk sütunundaki işaret değişikliklerinin sayısını bulun.$\epsilon$ sıfıra meyillidir.
Example
Karakteristik denklemi olan kontrol sisteminin kararlılığını bulalım,
$$s^4+2s^3+s^2+2s+1=0$$
Step 1 - Routh-Hurwitz stabilitesi için gerekli koşulu doğrulayın.
Karakteristik polinomun tüm katsayıları, $s^4+2s^3+s^2+2s+1$olumlu. Böylece, kontrol sistemi gerekli koşulu sağladı.
Step 2 - Verilen karakteristik polinom için Routh dizisini oluşturun.
$s^4$ |
$1$ |
$1$ |
$1$ |
$s^3$ |
|
|
|
$s^2$ |
$\frac{(1 \times 1)-(1 \times 1)}{1}=0$ |
$\frac{(1 \times 1)-(0 \times 1)}{1}=1$ |
|
$s^1$ |
|||
$s^0$ |
Sıra $s^3$elemanların ortak çarpanı 2'dir. Yani, tüm bu unsurlar 2'ye bölünmüştür.
Special case (i) - Satırın yalnızca ilk öğesi $s^2$sıfırdır. Öyleyse değiştir$\epsilon$ ve Routh masasını tamamlama sürecine devam edin.
$s^4$ |
1 |
1 |
1 |
$s^3$ |
1 |
1 |
|
$s^2$ |
$\epsilon$ |
1 |
|
$s^1$ |
$\frac{\left ( \epsilon \times 1 \right )-\left ( 1 \times 1 \right )}{\epsilon}=\frac{\epsilon-1}{\epsilon}$ |
||
$s^0$ |
1 |
Step 3 - Routh-Hurwitz stabilitesi için yeterli koşulu doğrulayın.
Gibi $\epsilon$ sıfırlanma eğilimindeyken, Routh tablosu şöyle olur.
$s^4$ |
1 |
1 |
1 |
$s^3$ |
1 |
1 |
|
$s^2$ |
0 |
1 |
|
$s^1$ |
-∞ |
||
$s^0$ |
1 |
Routh tablosunun ilk sütununda iki işaret değişikliği vardır. Bu nedenle, kontrol sistemi kararsızdır.
Routh dizisinin herhangi bir satırındaki tüm Elements sıfırdır
Bu durumda, şu iki adımı izleyin -
Sıfırlar satırının hemen üzerinde olan A (s) yardımcı denklemini yazın.
Yardımcı denklem A (s) 'yi s'ye göre farklılaştırın. Sıfırları bu katsayılarla doldurun.
Example
Karakteristik denklemi olan kontrol sisteminin kararlılığını bulalım,
$$s^5+3s^4+s^3+3s^2+s+3=0$$
Step 1 - Routh-Hurwitz stabilitesi için gerekli koşulu doğrulayın.
Verilen karakteristik polinomun tüm katsayıları pozitiftir. Böylece, kontrol sistemi gerekli koşulu sağladı.
Step 2 - Verilen karakteristik polinom için Routh dizisini oluşturun.
$s^5$ |
1 |
1 |
1 |
$s^4$ |
|
|
|
$s^3$ |
$\frac{(1 \times 1)-(1 \times 1)}{1}=0$ |
$\frac{(1 \times 1)-(1 \times 1)}{1}=0$ |
|
$s^2$ |
|||
$s^1$ |
|||
$s^0$ |
Sıra $s^4$ elemanların ortak çarpanı 3'tür. Yani tüm bu elemanlar 3'e bölünür.
Special case (ii) - Satırın tüm unsurları $s^3$sıfırdır. Öyleyse, satırın A (s) yardımcı denklemini yazın$s^4$.
$$A(s)=s^4+s^2+1$$
Yukarıdaki denklemi s'ye göre farklılaştırın.
$$\frac{\text{d}A(s)}{\text{d}s}=4s^3+2s$$
Bu katsayıları sıraya yerleştirin $s^3$.
$s^5$ |
1 |
1 |
1 |
$s^4$ |
1 |
1 |
1 |
$s^3$ |
|
|
|
$s^2$ |
$\frac{(2 \times 1)-(1 \times 1)}{2}=0.5$ |
$\frac{(2 \times 1)-(0 \times 1)}{2}=1$ |
|
$s^1$ |
$\frac{(0.5 \times 1)-(1 \times 2)}{0.5}=\frac{-1.5}{0.5}=-3$ |
||
$s^0$ |
1 |
Step 3 - Routh-Hurwitz stabilitesi için yeterli koşulu doğrulayın.
Routh tablosunun ilk sütununda iki işaret değişikliği vardır. Bu nedenle, kontrol sistemi kararsızdır.
Routh-Hurwitz kararlılık kriterinde, kapalı döngü kutuplarının 's' düzleminin sol yarısında mı yoksa 's' düzleminin sağ yarısında mı yoksa hayali bir eksende mi olduğunu bilebiliriz. Yani, kontrol sisteminin doğasını bulamıyoruz. Bu sınırlamanın üstesinden gelmek için kök lokusu olarak bilinen bir teknik vardır. Bu tekniği sonraki iki bölümde tartışacağız.
Kök konum diyagramında kapalı döngü kutuplarının yolunu gözlemleyebiliriz. Bu nedenle, kontrol sisteminin doğasını belirleyebiliriz. Bu teknikte, kapalı döngü kontrol sisteminin kararlılığını bilmek için bir açık döngü transfer fonksiyonu kullanacağız.
Kök Yerinin Temelleri
Kök lokusu, sistem K kazancını sıfırdan sonsuza değiştirerek karakteristik denklemin köklerinin lokusudur.
Kapalı döngü kontrol sisteminin karakteristik denkleminin şöyle olduğunu biliyoruz
$$1+G(s)H(s)=0$$
Temsil edebiliriz $G(s)H(s)$ gibi
$$G(s)H(s)=K\frac{N(s)}{D(s)}$$
Nerede,
K çarpan faktörü temsil eder
N (s) , "s" nin n inci derece polinomuna sahip (çarpanlarına ayrılmış) pay terimini temsil eder .
D (ler) payda terimi sahip olan (çarpanlarına) m temsil inci 's' polinom.
Vekil, $G(s)H(s)$ karakteristik denklemdeki değer.
$$1+k\frac{N(s)}{D(s)}=0$$
$$\Rightarrow D(s)+KN(s)=0$$
Case 1 − K = 0
Eğer $K=0$, sonra $D(s)=0$.
Bu, K sıfır olduğunda kapalı döngü kutuplarının açık döngü kutuplarına eşit olduğu anlamına gelir.
Case 2 − K = ∞
Yukarıdaki karakteristik denklemi şu şekilde yeniden yazın:
$$K\left(\frac{1}{K}+\frac{N(s)}{D(s)} \right )=0 \Rightarrow \frac{1}{K}+\frac{N(s)}{D(s)}=0$$
Vekil, $K = \infty$ yukarıdaki denklemde.
$$\frac{1}{\infty}+\frac{N(s)}{D(s)}=0 \Rightarrow \frac{N(s)}{D(s)}=0 \Rightarrow N(s)=0$$
Eğer $K=\infty$, sonra $N(s)=0$. Bu, K sonsuz olduğunda kapalı döngü kutuplarının açık döngü sıfırlarına eşit olduğu anlamına gelir.
Yukarıdaki iki durumdan, kök lokus dallarının açık döngü kutuplarında başlayıp açık döngü sıfırlarında sona erdiği sonucuna varabiliriz.
Açı Durumu ve Büyüklük Durumu
Kök lokus dalları üzerindeki noktalar açı koşulunu sağlar. Bu nedenle, açı koşulu, noktanın kök yer eğrisi dalında olup olmadığını bilmek için kullanılır. Kök yer eğrisi dalları üzerindeki noktalar için K değerini büyüklük koşulunu kullanarak bulabiliriz. Yani, noktalar için büyüklük koşulunu kullanabiliriz ve bu açı koşulunu sağlar.
Kapalı döngü kontrol sisteminin karakteristik denklemi
$$1+G(s)H(s)=0$$
$$\Rightarrow G(s)H(s)=-1+j0$$
phase angle nın-nin $G(s)H(s)$ dır-dir
$$\angle G(s)H(s)=\tan^{-1}\left ( \frac{0}{-1} \right )=(2n+1)\pi$$
angle conditionaçık döngü transfer fonksiyonunun açısının 180 0'ın tek katı olduğu noktadır .
Büyüklüğü $G(s)H(s)$ dır-dir -
$$|G(s)H(s)|=\sqrt {(-1)^2+0^2}=1$$
Büyüklük koşulu, açık döngü transfer fonksiyonunun büyüklüğünün bir olduğu noktanın (açı koşulunu sağlayan) olmasıdır.
root locuss-alanında bir grafik temsilidir ve gerçek eksen etrafında simetriktir. Çünkü açık döngü kutupları ve sıfırları, gerçek veya karmaşık eşlenik çiftler olarak değerlere sahip olan s-alanında mevcuttur. Bu bölümde, kök konumunun nasıl oluşturulacağını (çizileceğini) tartışalım.
Kök Yerinin Oluşturulması İçin Kurallar
Bir kök konumu oluşturmak için bu kuralları izleyin.
Rule 1 - 's' düzlemindeki açık döngü kutuplarını ve sıfırları bulun.
Rule 2 - Kök lokus dallarının sayısını bulun.
Kök lokus dallarının açık döngü kutuplarında başladığını ve açık döngü sıfırlarında sona erdiğini biliyoruz. Öyleyse, kök odağı dallarının sayısıN sonlu açık döngü kutuplarının sayısına eşittir P veya sonlu açık döngü sıfırlarının sayısı Z, Hangisi daha iyiyse.
Matematiksel olarak, kök lokus dallarının sayısını yazabiliriz N gibi
$N=P$ Eğer $P\geq Z$
$N=Z$ Eğer $P<Z$
Rule 3 - Tanımlayın ve çizin real axis root locus branches.
Bir noktadaki açık döngü transfer fonksiyonunun açısı 180 0'ın tek katı ise , o zaman bu nokta kök mahal üzerindedir. Gerçek eksendeki bir noktanın sol tarafında açık döngü kutuplarının tek sayısı ve sıfırları varsa, o nokta kök konum dalının üzerindedir. Bu nedenle, bu koşulu sağlayan noktaların dalı, kök lokus dalının gerçek eksenidir.
Rule 4 - Ağırlık merkezini ve asimptotların açısını bulun.
Eğer $P = Z$, sonra tüm kök yer eğrisi dalları sonlu açık döngü kutuplarında başlar ve sonlu açık döngü sıfırlarında biter.
Eğer $P > Z$ , sonra $Z$ kök lokus dallarının sayısı, sonlu açık döngü kutuplarında başlar ve sonlu açık döngü sıfırlarında biter ve $P − Z$ kök lokus dallarının sayısı, sonlu açık döngü kutuplarında başlar ve sonsuz açık döngü sıfırlarında sona erer.
Eğer $P < Z$ , sonra P sayısı kök yer eğrisi dalları sonlu açık döngü kutuplarında başlar ve sonlu açık döngü sıfırlarında biter ve $Z − P$ kök lokus dallarının sayısı sonsuz açık döngü kutuplarında başlar ve sonlu açık döngü sıfırlarında biter.
Öyleyse, bazı kök yer eğrisi dalları sonsuza yaklaşırken $P \neq Z$. Asimptotlar, bu kök odağı dallarının yönünü verir. Asimptotların gerçek eksendeki kesişme noktası olarak bilinircentroid.
Hesaplayabiliriz centroid α bu formülü kullanarak
$\alpha = \frac{\sum Real\: part\: of\: finite\: open\: loop\: poles\:-\sum Real\: part\: of\: finite\: open\: loop\: zeros}{P-Z}$
Açısının formülü asymptotes θ dır-dir
$$\theta=\frac{(2q+1)180^0}{P-Z}$$
Nerede,
$$q=0,1,2,....,(P-Z)-1$$
Rule 5 - Kök yer eğrisi dallarının sanal bir eksenle kesişme noktalarını bulun.
Kök yer eğrisi dalının sanal ekseni ve değerini kestiği noktayı hesaplayabiliriz. K bu noktada Routh dizisi yöntemini ve özel case (ii).
Routh dizisinin herhangi bir satırındaki tüm elemanlar sıfırsa, kök konum dalı sanal ekseni keser ve bunun tersi de geçerlidir.
Satırı, ilk öğeyi sıfır yaparsak, tüm satırın öğeleri sıfır olacak şekilde tanımlayın. Değerini bulunK bu kombinasyon için.
Bunu değiştirin Kyardımcı denklemdeki değer. Kök yer eğrisi dalının sanal bir eksenle kesişme noktasını alacaksınız.
Rule 6 - Break-away ve Break-in noktalarını bulun.
İki açık döngü kutbu arasında gerçek bir eksen kök lokus dalı varsa, o zaman bir break-away point bu iki açık döngü kutup arasında.
İki açık döngü sıfırı arasında gerçek bir eksen kök yer eğrisi dalı varsa, o zaman bir break-in point bu iki açık döngü sıfırı arasında.
Note - Ayrılma ve kırılma noktaları yalnızca gerçek eksen kök konum dallarında bulunur.
Ayrılma ve kırılma noktalarını bulmak için aşağıdaki adımları izleyin.
Yazmak $K$ açısından $s$ karakteristik denklemden $1 + G(s)H(s) = 0$.
Ayırt etmek $K$s'ye göre ve sıfıra eşit yapın. Bu değerleri değiştirin$s$ yukarıdaki denklemde.
Değerleri $s$ bunun için $K$ değer pozitiftir break points.
Rule 7 - Kalkış açısını ve varış açısını bulun.
Kalkış açısı ve varış açısı, sırasıyla karmaşık eşlenik açık döngü kutuplarında ve karmaşık eşlenik açık döngü sıfırlarında hesaplanabilir.
Formülü angle of departure $\phi_d$ dır-dir
$$\phi_d=180^0-\phi$$
Formülü angle of arrival $\phi_a$ dır-dir
$$\phi_a=180^0+\phi$$
Nerede,
$$\phi=\sum \phi_P-\sum \phi_Z$$
Misal
Şimdi açık döngü transfer fonksiyonuna sahip kontrol sisteminin kök lokusunu çizelim, $G(s)H(s)=\frac{K}{s(s+1)(s+5)}$
Step 1 - Verilen açık döngü transfer fonksiyonunun üç kutbu vardır. $s = 0, s = −1$ ve $s = −5$. Sıfır yok. Bu nedenle, kök lokus dallarının sayısı, açık döngü transfer fonksiyonunun kutup sayısına eşittir.
$$N=P=3$$

Üç kutup yerleştirilmiştir, yukarıdaki şekilde gösterilmiştir. Arasındaki çizgi parçası$s = −1$ ve $s = 0$gerçek eksendeki kök yerinin bir dalıdır. Ve gerçek eksendeki kök yerinin diğer dalı, solundaki çizgi bölümüdür.$s = −5$.
Step 2 - Centroid değerlerini ve asimptotların açısını verilen formülleri kullanarak alacağız.
Centroid $\alpha = −2$
Asimptotların açısı $\theta = 60^0,180^0$ ve $300^0$.
Centroid ve üç asimptot aşağıdaki şekilde gösterilmektedir.

Step 3 - İki asimptotun açıları olduğundan $60^0$ ve $300^0$iki kök odağı dalı hayali ekseni kesişir. Routh dizi yöntemini ve (ii) özel durumunu kullanarak, kök yer bölgesi dalları sanal ekseni$j\sqrt{5}$ ve $−j\sqrt{5}$.
Kutuplar arasındaki gerçek eksen kök lokus dalında bir kırılma noktası olacaktır. $s = −1$ ve $s = 0$. Kırılma noktasının hesaplanması için verilen prosedürü takip ederek şu şekilde alacağız:$s = −0.473$.
Verilen kontrol sistemi için kök konum diyagramı aşağıdaki şekilde gösterilmektedir.

Bu şekilde, herhangi bir kontrol sisteminin kök konum diyagramını çizebilir ve kapalı döngü transfer fonksiyonunun kutuplarının hareketini gözlemleyebilirsiniz.
Kök yer diyagramlarından, farklı sönümleme türleri için K değerlerinin aralığını bilebiliriz.
Açık Döngü Kutupları ve Sıfırları Eklemenin Kök Yer Eğrisi Üzerindeki Etkileri
Kök lokusu kaydırılabilir ‘s’ plane açık döngü kutuplarını ve açık döngü sıfırlarını ekleyerek.
Açık döngü transfer fonksiyonuna bir kutup eklersek, o zaman bazı kök konum dalları 's' düzleminin sağ yarısına doğru hareket edecektir. Bu nedenle sönümleme oranı$\delta$azalır. Bunun anlamı sönümlü frekans$\omega_d$ artar ve gecikme süresi gibi zaman alanı özellikleri $t_d$, yükselme zamanı $t_r$ ve yoğun zaman $t_p$azaltmak. Ancak, sistem kararlılığını etkiler.
Açık döngü transfer fonksiyonuna bir sıfırı dahil edersek, o zaman bazı kök konum dalları 's' düzleminin sol yarısına doğru hareket edecektir. Böylece kontrol sistemi kararlılığını artıracaktır. Bu durumda, sönümleme oranı$\delta$artışlar. Bunun anlamı sönümlü frekans$\omega_d$ azalır ve gecikme süresi gibi zaman alanı özellikleri $t_d$, yükselme zamanı $t_r$ ve yoğun zaman $t_p$ artırmak.
Bu nedenle, gereksinime bağlı olarak, açık döngü kutuplarını veya sıfırları transfer fonksiyonuna ekleyebiliriz (ekleyebiliriz).
Kontrol sistemlerinin zaman yanıt analizini ve ikinci derece kontrol sistemlerinin zaman alanı spesifikasyonlarını zaten tartışmıştık. Bu bölümde, kontrol sistemlerinin frekans yanıt analizini ve ikinci derece kontrol sistemlerinin frekans alanı özelliklerini tartışalım.
Frekans Tepkisi nedir?
Bir sistemin yanıtı, hem geçici yanıt hem de sabit durum yanıtı olarak bölünebilir. Fourier integrallerini kullanarak geçici yanıtı bulabiliriz. Bir sinüzoidal giriş sinyali için bir sistemin kararlı durum yanıtı,frequency response. Bu bölümde, sadece kararlı durum tepkisine odaklanacağız.
Bir Doğrusal Zamanla Değişmeyen (LTI) sisteme giriş olarak sinüzoidal bir sinyal uygulanırsa, o zaman aynı zamanda bir sinüzoidal sinyal olan kararlı durum çıkışı üretir. Giriş ve çıkış sinüzoidal sinyaller aynı frekansa, ancak farklı genliklere ve faz açılarına sahiptir.
Giriş sinyalinin -
$$r(t)=A\sin(\omega_0t)$$
The open loop transfer function will be −
$$G(s)=G(j\omega)$$
We can represent $G(j\omega)$ in terms of magnitude and phase as shown below.
$$G(j\omega)=|G(j\omega)| \angle G(j\omega)$$
Substitute, $\omega = \omega_0$ in the above equation.
$$G(j\omega_0)=|G(j\omega_0)| \angle G(j\omega_0)$$
The output signal is
$$c(t)=A|G(j\omega_0)|\sin(\omega_0t + \angle G(j\omega_0))$$
The amplitude of the output sinusoidal signal is obtained by multiplying the amplitude of the input sinusoidal signal and the magnitude of $G(j\omega)$ at $\omega = \omega_0$.
The phase of the output sinusoidal signal is obtained by adding the phase of the input sinusoidal signal and the phase of $G(j\omega)$ at $\omega = \omega_0$.
Where,
A is the amplitude of the input sinusoidal signal.
ω0 is angular frequency of the input sinusoidal signal.
We can write, angular frequency $\omega_0$ as shown below.
$$\omega_0=2\pi f_0$$
Here, $f_0$ is the frequency of the input sinusoidal signal. Similarly, you can follow the same procedure for closed loop control system.
Frequency Domain Specifications
The frequency domain specifications are resonant peak, resonant frequency and bandwidth.
Consider the transfer function of the second order closed loop control system as,
$$T(s)=\frac{C(s)}{R(s)}=\frac{\omega_n^2}{s^2+2\delta\omega_ns+\omega_n^2}$$
Substitute, $s = j\omega$ in the above equation.
$$T(j\omega)=\frac{\omega_n^2}{(j\omega)^2+2\delta\omega_n(j\omega)+\omega_n^2}$$
$$\Rightarrow T(j\omega)=\frac{\omega_n^2}{-\omega^2+2j\delta\omega\omega_n+\omega_n^2}=\frac{\omega_n^2}{\omega_n^2\left ( 1-\frac{\omega^2}{\omega_n^2}+\frac{2j\delta\omega}{\omega_n} \right )}$$
$$\Rightarrow T(j\omega)=\frac{1}{\left ( 1-\frac{\omega^2}{\omega_n^2} \right )+j\left ( \frac{2\delta\omega}{\omega_n} \right )}$$
Let, $\frac{\omega}{\omega_n}=u$ Substitute this value in the above equation.
$$T(j\omega)=\frac{1}{(1-u^2)+j(2\delta u)}$$
Magnitude of $T(j\omega)$ is -
$$M=|T(j\omega)|=\frac{1}{\sqrt {(1-u^2)^2+(2\delta u)^2}}$$
Phase of $T(j\omega)$ is -
$$\angle T(j\omega)=-tan^{-1}\left( \frac{2\delta u}{1-u^2} \right )$$
Resonant Frequency
It is the frequency at which the magnitude of the frequency response has peak value for the first time. It is denoted by $\omega_r$. At $\omega = \omega_r$, the first derivate of the magnitude of $T(j\omega)$ is zero.
Differentiate $M$ with respect to $u$.
$$\frac{\text{d}M}{\text{d}u}=-\frac{1}{2}\left [ (1-u^2)^2+(2\delta u)^2 \right ]^{\frac{-3}{2}} \left [2(1-u^2)(-2u)+2(2\delta u)(2\delta) \right ]$$
$$\Rightarrow \frac{\text{d}M}{\text{d}u}=-\frac{1}{2}\left [ (1-u^2)^2+(2\delta u)^2 \right ]^{\frac{-3}{2}} \left [4u(u^2-1 +2\delta^2) \right ]$$
Substitute, $u=u_r$ and $\frac{\text{d}M}{\text{d}u}==0$ in the above equation.
$$0=-\frac{1}{2}\left [ (1-u_r^2)^2+(2\delta u_r)^2 \right ]^{-\frac{3}{2}}\left [ 4u_r(u_r^2-1 +2\delta^2) \right ]$$
$$\Rightarrow 4u_r(u_r^2-1 +2\delta^2)=0$$
$$\Rightarrow u_r^2-1+2\delta^2=0$$
$$\Rightarrow u_r^2=1-2\delta^2$$
$$\Rightarrow u_r=\sqrt{1-2\delta^2}$$
Substitute, $u_r=\frac{\omega_r}{\omega_n}$ in the above equation.
$$\frac{\omega_r}{\omega_n}=\sqrt{1-2\delta^2}$$
$$\Rightarrow \omega_r=\omega_n \sqrt{1-2\delta^2}$$
Resonant Peak
It is the peak (maximum) value of the magnitude of $T(j\omega)$. It is denoted by $M_r$.
At $u = u_r$, the Magnitude of $T(j\omega)$ is -
$$M_r=\frac{1}{\sqrt{(1-u_r^2)^2+(2\delta u_r)^2}}$$
Substitute, $u_r = \sqrt{1 − 2\delta^2}$ and $1 − u_r^2 = 2\delta^2$ in the above equation.
$$M_r=\frac{1}{\sqrt{(2\delta^2)^2+(2\delta \sqrt{1-2\delta^2})^2}}$$
$$\Rightarrow M_r=\frac{1}{2\delta \sqrt {1-\delta^2}}$$
Resonant peak in frequency response corresponds to the peak overshoot in the time domain transient response for certain values of damping ratio $\delta$. So, the resonant peak and peak overshoot are correlated to each other.
Bandwidth
It is the range of frequencies over which, the magnitude of $T(j\omega)$ drops to 70.7% from its zero frequency value.
At $\omega = 0$, the value of $u$ will be zero.
Substitute, $u = 0$ in M.
$$M=\frac{1}{\sqrt {(1-0^2)^2+(2\delta(0))^2}}=1$$
Therefore, the magnitude of $T(j\omega)$ is one at $\omega = 0$.
At 3-dB frequency, the magnitude of $T(j\omega)$ will be 70.7% of magnitude of $T(j\omega)$ at $\omega = 0$.
i.e., at $\omega = \omega_B, M = 0.707(1) = \frac{1}{\sqrt{2}}$
$$\Rightarrow M=\frac{1}{\sqrt{2}}=\frac{1}{\sqrt{(1-u_b^2)^2+(2\delta u_b)^2}}$$
$$\Rightarrow 2=(1-u_b^2)^2+(2\delta)^2 u_b^2$$
Let, $u_b^2=x$
$$\Rightarrow 2=(1-x)^2+(2\delta)^2 x$$
$$\Rightarrow x^2+(4\delta^2-2)x-1=0$$
$$\Rightarrow x=\frac{-(4\delta^2 -2)\pm \sqrt{(4\delta^2-2)^2+4}}{2}$$
Consider only the positive value of x.
$$x=1-2\delta^2+\sqrt {(2\delta^2-1)^2+1}$$
$$\Rightarrow x=1-2\delta^2+\sqrt {(2-4\delta^2+4\delta^4)}$$
Substitute, $x=u_b^2=\frac{\omega_b^2}{\omega_n^2}$
$$\frac{\omega_b^2}{\omega_n^2}=1-2\delta^2+\sqrt {(2-4\delta^2+4\delta^4)}$$
$$\Rightarrow \omega_b=\omega_n \sqrt {1-2\delta^2+\sqrt {(2-4\delta^2+4\delta^4)}}$$
Bandwidth $\omega_b$ in the frequency response is inversely proportional to the rise time $t_r$ in the time domain transient response.
The Bode plot or the Bode diagram consists of two plots −
- Magnitude plot
- Phase plot
In both the plots, x-axis represents angular frequency (logarithmic scale). Whereas, yaxis represents the magnitude (linear scale) of open loop transfer function in the magnitude plot and the phase angle (linear scale) of the open loop transfer function in the phase plot.
The magnitude of the open loop transfer function in dB is -
$$M=20\: \log|G(j\omega)H(j\omega)|$$
The phase angle of the open loop transfer function in degrees is -
$$\phi=\angle G(j\omega)H(j\omega)$$
Note − The base of logarithm is 10.
Basic of Bode Plots
The following table shows the slope, magnitude and the phase angle values of the terms present in the open loop transfer function. This data is useful while drawing the Bode plots.
| Type of term | G(jω)H(jω) | Slope(dB/dec) | Magnitude (dB) | Phase angle(degrees) |
|---|---|---|---|---|
Constant |
$K$ |
$0$ |
$20 \log K$ |
$0$ |
Zero at origin |
$j\omega$ |
$20$ |
$20 \log \omega$ |
$90$ |
‘n’ zeros at origin |
$(j\omega)^n$ |
$20\: n$ |
$20\: n \log \omega$ |
$90\: n$ |
Pole at origin |
$\frac{1}{j\omega}$ |
$-20$ |
$-20 \log \omega$ |
$-90 \: or \: 270$ |
‘n’ poles at origin |
$\frac{1}{(j\omega)^n}$ |
$-20\: n$ |
$-20 \: n \log \omega$ |
$-90 \: n \: or \: 270 \: n$ |
Simple zero |
$1+j\omega r$ |
$20$ |
$0\: for\: \omega < \frac{1}{r}$ $20\: \log \omega r\: for \: \omega > \frac{1}{r}$ |
$0 \: for \: \omega < \frac{1}{r}$ $90 \: for \: \omega > \frac{1}{r}$ |
Simple pole |
$\frac{1}{1+j\omega r}$ |
$-20$ |
$0\: for\: \omega < \frac{1}{r}$ $-20\: \log \omega r\: for\: \omega > \frac{1}{r}$ |
$0 \: for \: \omega < \frac{1}{r}$ $-90\: or \: 270 \: for\: \omega > \frac{1}{r}$ |
Second order derivative term |
$\omega_n^2\left ( 1-\frac{\omega^2}{\omega_n^2}+\frac{2j\delta\omega}{\omega_n} \right )$ |
$40$ |
$40\: \log\: \omega_n\: for \: \omega < \omega_n$ $20\: \log\:(2\delta\omega_n^2)\: for \: \omega=\omega_n$ $40 \: \log \: \omega\:for \:\omega > \omega_n$ |
$0 \: for \: \omega < \omega_n$ $90 \: for \: \omega = \omega_n$ $180 \: for \: \omega > \omega_n$ |
Second order integral term |
$\frac{1}{\omega_n^2\left ( 1-\frac{\omega^2}{\omega_n^2}+\frac{2j\delta\omega}{\omega_n} \right )}$ |
$-40$ |
$-40\: \log\: \omega_n\: for \: \omega < \omega_n$ $-20\: \log\:(2\delta\omega_n^2)\: for \: \omega=\omega_n$ $-40 \: \log \: \omega\:for \:\omega > \omega_n$ |
$-0 \: for \: \omega < \omega_n$ $-90 \: for \: \omega = \omega_n$ $-180 \: for \: \omega > \omega_n$ |
Consider the open loop transfer function $G(s)H(s) = K$.
Magnitude $M = 20\: \log K$ dB
Phase angle $\phi = 0$ degrees
If $K = 1$, then magnitude is 0 dB.
If $K > 1$, then magnitude will be positive.
If $K < 1$, then magnitude will be negative.
The following figure shows the corresponding Bode plot.


The magnitude plot is a horizontal line, which is independent of frequency. The 0 dB line itself is the magnitude plot when the value of K is one. For the positive values of K, the horizontal line will shift $20 \:\log K$ dB above the 0 dB line. For the negative values of K, the horizontal line will shift $20\: \log K$ dB below the 0 dB line. The Zero degrees line itself is the phase plot for all the positive values of K.
Consider the open loop transfer function $G(s)H(s) = s$.
Magnitude $M = 20 \log \omega$ dB
Phase angle $\phi = 90^0$
At $\omega = 0.1$ rad/sec, the magnitude is -20 dB.
At $\omega = 1$ rad/sec, the magnitude is 0 dB.
At $\omega = 10$ rad/sec, the magnitude is 20 dB.
The following figure shows the corresponding Bode plot.


The magnitude plot is a line, which is having a slope of 20 dB/dec. This line started at $\omega = 0.1$ rad/sec having a magnitude of -20 dB and it continues on the same slope. It is touching 0 dB line at $\omega = 1$ rad/sec. In this case, the phase plot is 900 line.
Consider the open loop transfer function $G(s)H(s) = 1 + s\tau$.
Magnitude $M = 20\: log \sqrt{1 + \omega^2\tau^2}$ dB
Phase angle $\phi = \tan^{-1}\omega\tau$ degrees
For $ω < \frac{1}{\tau}$ , the magnitude is 0 dB and phase angle is 0 degrees.
For $\omega > \frac{1}{\tau}$ , the magnitude is $20\: \log \omega\tau$ dB and phase angle is 900.
The following figure shows the corresponding Bode plot.

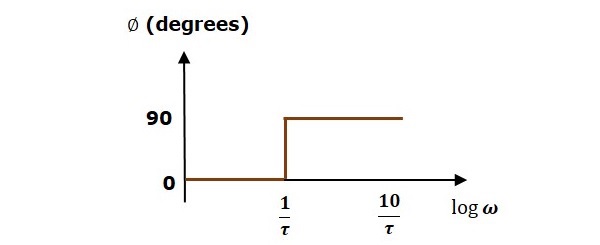
The magnitude plot is having magnitude of 0 dB upto $\omega=\frac{1}{\tau}$ rad/sec. From $\omega = \frac{1}{\tau}$ rad/sec, it is having a slope of 20 dB/dec. In this case, the phase plot is having phase angle of 0 degrees up to $\omega = \frac{1}{\tau}$ rad/sec and from here, it is having phase angle of 900. This Bode plot is called the asymptotic Bode plot.
As the magnitude and the phase plots are represented with straight lines, the Exact Bode plots resemble the asymptotic Bode plots. The only difference is that the Exact Bode plots will have simple curves instead of straight lines.
Similarly, you can draw the Bode plots for other terms of the open loop transfer function which are given in the table.
In this chapter, let us understand in detail how to construct (draw) Bode plots.
Rules for Construction of Bode Plots
Follow these rules while constructing a Bode plot.
Represent the open loop transfer function in the standard time constant form.
Substitute, $s=j\omega$ in the above equation.
Find the corner frequencies and arrange them in ascending order.
Consider the starting frequency of the Bode plot as 1/10th of the minimum corner frequency or 0.1 rad/sec whichever is smaller value and draw the Bode plot upto 10 times maximum corner frequency.
Draw the magnitude plots for each term and combine these plots properly.
Draw the phase plots for each term and combine these plots properly.
Note − The corner frequency is the frequency at which there is a change in the slope of the magnitude plot.
Example
Consider the open loop transfer function of a closed loop control system
$$G(s)H(s)=\frac{10s}{(s+2)(s+5)}$$
Let us convert this open loop transfer function into standard time constant form.
$$G(s)H(s)=\frac{10s}{2\left( \frac{s}{2}+1 \right )5 \left( \frac{s}{5}+1 \right )}$$
$$\Rightarrow G(s)H(s)=\frac{s}{\left( 1+\frac{s}{2} \right )\left( 1+\frac{s}{5} \right )}$$
So, we can draw the Bode plot in semi log sheet using the rules mentioned earlier.
Stability Analysis using Bode Plots
From the Bode plots, we can say whether the control system is stable, marginally stable or unstable based on the values of these parameters.
- Gain cross over frequency and phase cross over frequency
- Gain margin and phase margin
Phase Cross over Frequency
The frequency at which the phase plot is having the phase of -1800 is known as phase cross over frequency. It is denoted by $\omega_{pc}$. The unit of phase cross over frequency is rad/sec.
Gain Cross over Frequency
The frequency at which the magnitude plot is having the magnitude of zero dB is known as gain cross over frequency. It is denoted by $\omega_{gc}$. The unit of gain cross over frequency is rad/sec.
The stability of the control system based on the relation between the phase cross over frequency and the gain cross over frequency is listed below.
If the phase cross over frequency $\omega_{pc}$ is greater than the gain cross over frequency $\omega_{gc}$, then the control system is stable.
If the phase cross over frequency $\omega_{pc}$ is equal to the gain cross over frequency $\omega_{gc}$, then the control system is marginally stable.
If the phase cross over frequency $\omega_{pc}$ is less than the gain cross over frequency $\omega_{gc}$, then the control system is unstable.
Gain Margin
Gain margin $GM$ is equal to negative of the magnitude in dB at phase cross over frequency.
$$GM=20\log\left( \frac{1}{M_{pc}}\right )=20logM_{pc}$$
Where, $M_{pc}$ is the magnitude at phase cross over frequency. The unit of gain margin (GM) is dB.
Phase Margin
The formula for phase margin $PM$ is
$$PM=180^0+\phi_{gc}$$
Where, $\phi_{gc}$ is the phase angle at gain cross over frequency. The unit of phase margin is degrees.
The stability of the control system based on the relation between gain margin and phase margin is listed below.
If both the gain margin $GM$ and the phase margin $PM$ are positive, then the control system is stable.
If both the gain margin $GM$ and the phase margin $PM$ are equal to zero, then the control system is marginally stable.
If the gain margin $GM$ and / or the phase margin $PM$ are/is negative, then the control system is unstable.
In the previous chapters, we discussed the Bode plots. There, we have two separate plots for both magnitude and phase as the function of frequency. Let us now discuss about polar plots. Polar plot is a plot which can be drawn between magnitude and phase. Here, the magnitudes are represented by normal values only.
The polar form of $G(j\omega)H(j\omega)$ is
$$G(j\omega)H(j\omega)=|G(j\omega)H(j\omega)| \angle G(j\omega)H(j\omega)$$
The Polar plot is a plot, which can be drawn between the magnitude and the phase angle of $G(j\omega)H(j\omega)$ by varying $\omega$ from zero to ∞. The polar graph sheet is shown in the following figure.

This graph sheet consists of concentric circles and radial lines. The concentric circles and the radial lines represent the magnitudes and phase angles respectively. These angles are represented by positive values in anti-clock wise direction. Similarly, we can represent angles with negative values in clockwise direction. For example, the angle 2700 in anti-clock wise direction is equal to the angle −900 in clockwise direction.
Rules for Drawing Polar Plots
Follow these rules for plotting the polar plots.
Substitute, $s = j\omega$ in the open loop transfer function.
Write the expressions for magnitude and the phase of $G(j\omega)H(j\omega)$.
Find the starting magnitude and the phase of $G(j\omega)H(j\omega)$ by substituting $\omega = 0$. So, the polar plot starts with this magnitude and the phase angle.
Find the ending magnitude and the phase of $G(j\omega)H(j\omega)$ by substituting $\omega = \infty$. So, the polar plot ends with this magnitude and the phase angle.
Check whether the polar plot intersects the real axis, by making the imaginary term of $G(j\omega)H(j\omega)$ equal to zero and find the value(s) of $\omega$.
Check whether the polar plot intersects the imaginary axis, by making real term of $G(j\omega)H(j\omega)$ equal to zero and find the value(s) of $\omega$.
For drawing polar plot more clearly, find the magnitude and phase of $G(j\omega)H(j\omega)$ by considering the other value(s) of $\omega$.
Example
Consider the open loop transfer function of a closed loop control system.
$$G(s)H(s)=\frac{5}{s(s+1)(s+2)}$$
Let us draw the polar plot for this control system using the above rules.
Step 1 − Substitute, $s = j\omega$ in the open loop transfer function.
$$G(j\omega)H(j\omega)=\frac{5}{j\omega(j\omega+1)(j\omega+2)}$$
The magnitude of the open loop transfer function is
$$M=\frac{5}{\omega(\sqrt{\omega^2+1})(\sqrt{\omega^2+4})}$$
The phase angle of the open loop transfer function is
$$\phi=-90^0-\tan^{-1}\omega-\tan^{-1}\frac{\omega}{2}$$
Step 2 − The following table shows the magnitude and the phase angle of the open loop transfer function at $\omega = 0$ rad/sec and $\omega = \infty$ rad/sec.
| Frequency (rad/sec) | Magnitude | Phase angle(degrees) |
|---|---|---|
| 0 | ∞ | -90 or 270 |
| ∞ | 0 | -270 or 90 |
So, the polar plot starts at (∞,−900) and ends at (0,−2700). The first and the second terms within the brackets indicate the magnitude and phase angle respectively.
Step 3 − Based on the starting and the ending polar co-ordinates, this polar plot will intersect the negative real axis. The phase angle corresponding to the negative real axis is −1800 or 1800. So, by equating the phase angle of the open loop transfer function to either −1800 or 1800, we will get the $\omega$ value as $\sqrt{2}$.
By substituting $\omega = \sqrt{2}$ in the magnitude of the open loop transfer function, we will get $M = 0.83$. Therefore, the polar plot intersects the negative real axis when $\omega = \sqrt{2}$ and the polar coordinate is (0.83,−1800).
So, we can draw the polar plot with the above information on the polar graph sheet.
Nyquist plots are the continuation of polar plots for finding the stability of the closed loop control systems by varying ω from −∞ to ∞. That means, Nyquist plots are used to draw the complete frequency response of the open loop transfer function.
Nyquist Stability Criterion
The Nyquist stability criterion works on the principle of argument. It states that if there are P poles and Z zeros are enclosed by the ‘s’ plane closed path, then the corresponding $G(s)H(s)$ plane must encircle the origin $P − Z$ times. So, we can write the number of encirclements N as,
$$N=P-Z$$
If the enclosed ‘s’ plane closed path contains only poles, then the direction of the encirclement in the $G(s)H(s)$ plane will be opposite to the direction of the enclosed closed path in the ‘s’ plane.
If the enclosed ‘s’ plane closed path contains only zeros, then the direction of the encirclement in the $G(s)H(s)$ plane will be in the same direction as that of the enclosed closed path in the ‘s’ plane.
Let us now apply the principle of argument to the entire right half of the ‘s’ plane by selecting it as a closed path. This selected path is called the Nyquist contour.
We know that the closed loop control system is stable if all the poles of the closed loop transfer function are in the left half of the ‘s’ plane. So, the poles of the closed loop transfer function are nothing but the roots of the characteristic equation. As the order of the characteristic equation increases, it is difficult to find the roots. So, let us correlate these roots of the characteristic equation as follows.
The Poles of the characteristic equation are same as that of the poles of the open loop transfer function.
The zeros of the characteristic equation are same as that of the poles of the closed loop transfer function.
We know that the open loop control system is stable if there is no open loop pole in the the right half of the ‘s’ plane.
i.e.,$P=0 \Rightarrow N=-Z$
We know that the closed loop control system is stable if there is no closed loop pole in the right half of the ‘s’ plane.
i.e.,$Z=0 \Rightarrow N=P$
Nyquist stability criterionkritik nokta (1 + j0) etrafındaki daire sayısının, 's' düzleminin sağ yarısındaki açık döngü transfer fonksiyonunun kutuplarından başka bir şey olmayan karakteristik denklemin kutuplarına eşit olması gerektiğini belirtir. Başlangıçtaki (1 + j0) 'a kayma, karakteristik denklem düzlemini verir.
Nyquist Grafikleri Çizme Kuralları
Nyquist planlarını çizmek için bu kuralları izleyin.
Açık döngü transfer fonksiyonunun kutuplarını ve sıfırlarını bulun $G(s)H(s)$ in 's' düzleminde.
Kutupsal grafiği değiştirerek çizin $\omega$sıfırdan sonsuza. S = 0'da kutup veya sıfır varsa, o zaman değişken$\omega$ Kutupsal grafik çizmek için 0 + 'dan sonsuza.
Değerleri için yukarıdaki kutupsal grafiğin ayna görüntüsünü çizin $\omega$−∞'dan sıfıra (0 - s = 0'da herhangi bir kutup veya sıfır varsa).
Sonsuz yarıçaplı yarım dairelerin sayısı, başlangıçtaki kutupların veya sıfırların sayısına eşit olacaktır. Sonsuz yarıçaplı yarım daire, kutupsal grafiğin ayna görüntüsünün bittiği noktada başlayacaktır. Ve bu sonsuz yarıçaplı yarım daire, kutupsal grafiğin başladığı noktada sona erecek.
Nyquist grafiğini çizdikten sonra, Nyquist kararlılık kriterini kullanarak kapalı döngü kontrol sisteminin kararlılığını bulabiliriz. Kritik nokta (-1 + j0) kuşatmanın dışında yer alıyorsa, kapalı döngü kontrol sistemi kesinlikle kararlıdır.
Nyquist Grafiklerini Kullanarak Kararlılık Analizi
Nyquist grafiklerinden, bu parametrelerin değerlerine dayanarak kontrol sisteminin kararlı mı, marjinal olarak kararlı mı yoksa kararsız mı olduğunu belirleyebiliriz.
- Çapraz frekans ve faz geçiş frekansı kazanın
- Marj ve faz marjı kazanın
Faz Geçiş Frekansı
Nyquist grafiğinin negatif gerçek eksenle kesiştiği frekans (faz açısı 180 ° 'dir ),phase cross over frequency. İle gösterilir$\omega_{pc}$.
Çapraz Frekans Kazanç
Nyquist grafiğinin bir büyüklüğe sahip olduğu frekans, gain cross over frequency. İle gösterilir$\omega_{gc}$.
Faz geçiş frekansı ile kazanç geçiş frekansı arasındaki ilişkiye dayalı kontrol sisteminin kararlılığı aşağıda listelenmiştir.
Faz frekansı geçerse $\omega_{pc}$ frekans üzerinden geçen kazançtan daha büyüktür $\omega_{gc}$, o zaman kontrol sistemi stable.
Faz frekansı geçerse $\omega_{pc}$ frekans üzerinden geçiş kazancına eşittir $\omega_{gc}$, o zaman kontrol sistemi marginally stable.
Faz geçiş frekansı ise $\omega_{pc}$ çapraz frekans kazancından daha azdır $\omega_{gc}$, o zaman kontrol sistemi unstable.
Marj Kazanma
Kazanç marjı $GM$ frekans üzerinden geçiş fazında Nyquist grafiğinin büyüklüğünün tersine eşittir.
$$GM=\frac{1}{M_{pc}}$$
Nerede, $M_{pc}$ faz geçiş frekansında normal ölçekte büyüklüktür.
Faz Marjı
Faz marjı $PM$180 0'ın toplamına ve kazanç geçiş frekansındaki faz açısına eşittir .
$$PM=180^0+\phi_{gc}$$
Nerede, $\phi_{gc}$ frekans üzerinden geçen kazançtaki faz açısıdır.
Kazanç marjı ile faz marjı arasındaki ilişkiye dayalı kontrol sisteminin kararlılığı aşağıda listelenmiştir.
Kazanç marjı $GM$ birden büyüktür ve faz marjı $PM$ pozitifse, kontrol sistemi stable.
Kazanç marjı $GM$ bire eşittir ve faz marjı $PM$ sıfır derece ise, kontrol sistemi marginally stable.
Kazanç marjı $GM$ birden azdır ve / veya faz marjı $PM$ negatifse, kontrol sistemi unstable.
Üç tür kompansatör vardır - gecikmeli, ileri ve gecikmeli kompansatörler. Bunlar en yaygın olarak kullanılır.
Gecikme Dengeleyici
Gecikme Dengeleyici, sinüzoidal bir giriş uygulandığında faz gecikmesine sahip sinüzoidal bir çıktı üreten bir elektrik ağıdır. 'S' alanındaki gecikme kompansatör devresi aşağıdaki şekilde gösterilmektedir.

Burada kondansatör direnç ile seri halindedir $R_2$ ve çıktı bu kombinasyonda ölçülür.
Bu gecikme kompansatörünün transfer işlevi -
$$\frac{V_o(s)}{V_i(s)}=\frac{1}{\alpha} \left( \frac{s+\frac{1}{\tau}}{s+\frac{1}{\alpha\tau}} \right )$$
Nerede,
$$\tau=R_2C$$
$$\alpha=\frac{R_1+R_2}{R_2}$$
Yukarıdaki denklemden, $\alpha$ her zaman birden büyüktür.
Transfer fonksiyonundan, gecikme kompansatörünün bir kutbu olduğu sonucuna varabiliriz. $s = − \frac{1}{\alpha \tau}$ ve bir sıfır $s = −\frac{1}{\tau}$. Bu, gecikmeli kompansatörün kutup sıfır konfigürasyonunda kutbun orijine daha yakın olacağı anlamına gelir.
Vekil, $s = j\omega$ transfer fonksiyonunda.
$$\frac{V_o(j\omega)}{V_i(j\omega)}=\frac{1}{\alpha}\left( \frac{j\omega+\frac{1}{\tau}}{j\omega+\frac{1}{\alpha\tau}}\right )$$
Faz açısı $\phi = \tan^{−1} \omega\tau − tan^{−1} \alpha\omega\tau$
Çıkış sinüzoidal sinyalin fazının, giriş sinüzoidal sinyalin faz açılarının ve transfer fonksiyonunun toplamına eşit olduğunu biliyoruz.
Bu nedenle, bu kompansatörün çıkışında faz gecikmesini üretmek için transfer fonksiyonunun faz açısının negatif olması gerekir. Bu ne zaman olacak$\alpha > 1$.
Kurşun Dengeleyici
Kurşun dengeleyici, sinüzoidal bir giriş uygulandığında faz ucuna sahip sinüzoidal bir çıktı üreten bir elektrik ağıdır. 'S' alanındaki kurşun kompansatör devresi aşağıdaki şekilde gösterilmektedir.

Burada kondansatör dirence paraleldir $R_1$ ve çıktı, direnç $ R_2 boyunca ölçülür.
Bu kurşun kompansatörün transfer işlevi -
$$ \ frac {V_o (s)} {V_i (s)} = \ beta \ left (\ frac {s \ tau + 1} {\ beta s \ tau + 1} \ right) $$
Nerede,
$$ \ tau = R_1C $$
$$ \ beta = \ frac {R_2} {R_1 + R_2} $$
Transfer fonksiyonundan, kurşun kompansatörün $ s = - \ frac {1} {\ beta} konumunda kutbu olduğu sonucuna varabiliriz.$ and zero at $s = - \ frac {1} {\ beta \ tau} $.
Transfer işlevinde $ s = j \ omega $ yerine koyun.
$$ \ frac {V_o (j \ omega)} {V_i (j \ omega)} = \ beta \ left (\ frac {j \ omega \ tau + 1} {\ beta j \ omega \ tau + 1} \ right ) $$
Faz açısı $ \ phi = tan ^ {- 1} \ omega \ tau - tan ^ {- 1} \ beta \ omega \ tau $
Çıkış sinüzoidal sinyalin fazının, giriş sinüzoidal sinyalin faz açılarının ve transfer fonksiyonunun toplamına eşit olduğunu biliyoruz.
Bu nedenle, bu kompansatörün çıkışında faz kurşun üretmek için transfer fonksiyonunun faz açısının pozitif olması gerekir. Bu $ 0 <\ beta <1 $ olduğunda gerçekleşir. Bu nedenle, kurşun kompansatörün kutup sıfır konfigürasyonunda sıfır orijine daha yakın olacaktır.
Gecikmeli Kurşun Dengeleyici
Lag-Lead kompansatör, bir frekans bölgesinde faz gecikmesi ve diğer frekans bölgesinde faz öncüsü üreten bir elektrik şebekesidir. Hem gecikme hem de öncü kompansatörlerin bir kombinasyonudur. 'S' alanındaki gecikmeli kurşun kompansatör devresi aşağıdaki şekilde gösterilmektedir.

Bu devre, her iki kompansatör de kademeli gibi görünüyor. Dolayısıyla, bu devrenin transfer fonksiyonu lead ve gecikme kompansatörlerinin transfer fonksiyonlarının ürünü olacaktır.
$$ \ frac {V_o (s)} {V_i (s)} = \ beta \ left (\ frac {s \ tau_1 + 1} {\ beta s \ tau_1 + 1} \ right) \ frac {1} {\ alpha} \ left (\ frac {s + \ frac {1} {\ tau_2}} {s + \ frac {1} {\ alpha \ tau_2}} \ right) $$
$ \ Alpha \ beta = 1 $ biliyoruz.
$$ \ Rightarrow \ frac {V_o (s)} {V_i (s)} = \ left (\ frac {s + \ frac {1} {\ tau_1}} {s + \ frac {1} {\ beta \ tau_1}} \ right) \ left (\ frac {s + \ frac {1} {\ tau_2}} {s + \ frac {1} {\ alpha \ tau_2}} \ right) $$
Nerede,
$$ \ tau_1 = R_1C_1 $$
$$ \ tau_2 = R_2C_2 $$
Kontrol sistemlerinin performansını iyileştirmek için çeşitli kontrolör türleri kullanılır. Bu bölümde, orantılı, türev ve integral kontrolörler gibi temel kontrolörleri tartışacağız.
Orantılı Kontrolör
Orantılı kontrolör, hata sinyaliyle orantılı bir çıktı üretir.
$$ u (t) \ propto e (t) $$
$$ \ Rightarrow u (t) = K_P e (t) $$
Her iki tarafa da Laplace dönüşümü uygulayın -
$$ U (s) = K_P E $ $$
$$ \ frac {U (s)} {E (s)} = K_P $$
Bu nedenle, oransal kontrolörün transfer fonksiyonu $ K_P $ 'dır.
Nerede,
U (s), u (t) çalıştırma sinyalinin Laplace dönüşümüdür
E (s), e (t) hata sinyalinin Laplace dönüşümüdür.
K P orantılılık sabitidir
Birlik negatif geri beslemeli kapalı döngü kontrol sisteminin blok diyagramı oransal kontrolörle birlikte aşağıdaki şekilde gösterilmektedir.

Orantısal kontrolör, geçici yanıtı ihtiyaca göre değiştirmek için kullanılır.
Türev Denetleyici
Türev kontrolör, hata sinyalinin türevi olan bir çıktı üretir.
$$ u (t) = K_D \ frac {\ text {d} e (t)} {\ text {d} t} $$
Her iki tarafa da Laplace dönüşümü uygulayın.
$$ U (s) = K_D sE $ $$
$$ \ frac {U (s)} {E (s)} = K_D s $$
Bu nedenle, türev kontrolörün transfer fonksiyonu $ K_D s $ 'dır.
Burada, $ K_D $ türev sabitidir.
Türev kontrolör ile birlikte birlik negatif geri beslemeli kapalı döngü kontrol sisteminin blok diyagramı aşağıdaki şekilde gösterilmektedir.

Türev kontrolör, kararsız kontrol sistemini kararlı hale getirmek için kullanılır.
Entegre Denetleyici
Entegre kontrolör, hata sinyalinin integrali olan bir çıktı üretir.
$$ u (t) = K_I \ int e (t) dt $$
Her iki tarafa da Laplace dönüşümü uygulayın -
$$ U (s) = \ frac {K_I E (s)} {s} $$
$$ \ frac {U (s)} {E (s)} = \ frac {K_I} {s} $$
Bu nedenle, integral denetleyicinin transfer işlevi $ \ frac {K_I} {s} $ 'dır.
$ K_I $ integral sabitidir.
Birlik negatif geri beslemeli kapalı döngü kontrol sisteminin blok diyagramı, integral kontrolör ile birlikte aşağıdaki şekilde gösterilmektedir.

Entegre kontrolör, kararlı durum hatasını azaltmak için kullanılır.
Şimdi temel kontrolörlerin kombinasyonunu tartışalım.
Orantılı Türev (PD) Denetleyicisi
Orantılı türev kontrolör, orantılı ve türev kontrolörlerin çıkışlarının birleşimi olan bir çıktı üretir.
$$ u (t) = K_P e (t) + K_D \ frac {\ text {d} e (t)} {\ text {d} t} $$
Her iki tarafa da Laplace dönüşümü uygulayın -
$$ U (s) = (K_P + K_D s) E (s) $$
$$ \ frac {U (s)} {E (s)} = K_P + K_D s $$
Bu nedenle, orantılı türev kontrolörün transfer fonksiyonu $ K_P + K_D s $ 'dır.
Orantılı türev kontrolör ile birlikte birlik negatif geri besleme kapalı döngü kontrol sisteminin blok diyagramı aşağıdaki şekilde gösterilmektedir.

Orantısal türev kontrolörü, kararlı durum hatasını etkilemeden kontrol sisteminin kararlılığını iyileştirmek için kullanılır.
Orantılı İntegral (PI) Denetleyici
Orantısal integral kontrolör, orantılı ve integral kontrolörlerin çıkışlarının kombinasyonu olan bir çıktı üretir.
$$ u (t) = K_P e (t) + K_I \ int e (t) dt $$
Her iki tarafa da Laplace dönüşümü uygulayın -
$$ U (s) = \ sol (K_P + \ frac {K_I} {s} \ sağ) E (s) $$
$$ \ frac {U (s)} {E (s)} = K_P + \ frac {K_I} {s} $$
Bu nedenle, orantılı integral denetleyicinin transfer işlevi $ K_P + \ frac {K_I} {s} $ şeklindedir.
Birlik negatif geri beslemeli kapalı döngü kontrol sisteminin blok diyagramı, orantılı integral kontrolör ile birlikte aşağıdaki şekilde gösterilmektedir.

Orantılı integral kontrolör, kontrol sisteminin kararlılığını etkilemeden kararlı durum hatasını azaltmak için kullanılır.
Orantılı İntegral Türev (PID) Denetleyicisi
Orantılı integral türev kontrolörü, orantılı, integral ve türev kontrolörlerin çıkışlarının kombinasyonu olan bir çıktı üretir.
$$ u (t) = K_P e (t) + K_I \ int e (t) dt + K_D \ frac {\ text {d} e (t)} {\ text {d} t} $$
Her iki tarafa da Laplace dönüşümü uygulayın -
$$ U (s) = \ sol (K_P + \ frac {K_I} {s} + K_D s \ sağ) E (s) $$
$$ \ frac {U (s)} {E (s)} = K_P + \ frac {K_I} {s} + K_D s $$
Bu nedenle, orantılı integral türev denetleyicisinin transfer fonksiyonu $ K_P + \ frac {K_I} {s} + K_D s $ 'dır.
Birlik negatif geri beslemeli kapalı döngü kontrol sisteminin blok diyagramı, orantılı integral türev kontrolörü ile birlikte aşağıdaki şekilde gösterilmektedir.

Orantısal integral türev kontrolörü, kontrol sisteminin kararlılığını iyileştirmek ve sabit durum hatasını azaltmak için kullanılır.
state space model Doğrusal Zamanla Değişmeyen (LTI) sistemin şu şekilde temsil edilebilir:
$$ \ dot {X} = AX + BU $$
$$ Y = CX + DU $$
Birinci ve ikinci denklemler sırasıyla durum denklemi ve çıktı denklemi olarak bilinir.
Nerede,
X ve $ \ dot {X} $ sırasıyla durum vektörü ve diferansiyel durum vektörüdür.
U ve Y sırasıyla giriş vektörü ve çıkış vektörüdür.
A, sistem matrisidir.
B ve C, girdi ve çıktı matrisleridir.
D, ileri besleme matrisidir.
Durum Uzay Modelinin Temel Kavramları
Bu bölümde yer alan aşağıdaki temel terminoloji.
Durum
Gelecekteki değerleri (çıktıları) tahmin etmek için sistemin geçmişini özetleyen bir değişkenler grubudur.
Durum değişkeni
Gerekli durum değişkenlerinin sayısı, sistemde mevcut olan depolama elemanlarının sayısına eşittir.
Examples - indüktörden akan akım, kapasitördeki voltaj
Devlet Vektör
Durum değişkenlerini eleman olarak içeren bir vektördür.
Önceki bölümlerde, kontrol sistemlerinin iki matematiksel modelini tartıştık. Bunlar diferansiyel denklem modeli ve transfer fonksiyonu modelidir. Durum uzayı modeli, bu iki matematiksel modelden herhangi birinden elde edilebilir. Şimdi bu iki yöntemi tek tek tartışalım.
Diferansiyel Denklemden Durum Uzayı Modeli
Aşağıdaki RLC devresi serisini düşünün. Bir giriş voltajına sahip, $ v_i (t)$ and the current flowing through the circuit is $i [t) $.

Bu devrede iki depolama elemanı (indüktör ve kondansatör) vardır. Dolayısıyla, durum değişkenlerinin sayısı ikiye eşittir ve bu durum değişkenleri indüktörden geçen akımdır, $ i (t)$ and the voltage across capacitor, $v_c (t) $.
Devreden çıkış voltajı, $ v_0 (t)$ is equal to the voltage across capacitor, $v_c (t) $.
$$ v_0 (t) = v_c (t) $$
Döngünün etrafına KVL uygulayın.
$$ v_i (t) = Ri (t) + L \ frac {\ text {d} i (t)} {\ text {d} t} + v_c (t) $$
$$ \ Rightarrow \ frac {\ text {d} i (t)} {\ text {d} t} = - \ frac {Ri (t)} {L} - \ frac {v_c (t)} {L} + \ frac {v_i (t)} {L} $$
Kondansatör üzerindeki voltaj -
$$ v_c (t) = \ frac {1} {C} \ int i (t) dt $$
Yukarıdaki denklemi zamana göre farklılaştırın.
$$ \ frac {\ text {d} v_c (t)} {\ text {d} t} = \ frac {i (t)} {C} $$
Durum vektörü, $ X = \ begin {bmatrix} i (t) \\ v_c (t) \ end {bmatrix} $
Diferansiyel durum vektörü, $ \ dot {X} = \ begin {bmatrix} \ frac {\ text {d} i (t)} {\ text {d} t} \\\ frac {\ text {d} v_c (t )} {\ text {d} t} \ end {bmatrix} $
Diferansiyel denklemleri ve çıktı denklemini aşağıdaki gibi standart durum uzayı modeline yerleştirebiliriz:
$$ \ dot {X} = \ begin {bmatrix} \ frac {\ text {d} i (t)} {\ text {d} t} \\\ frac {\ text {d} v_c (t)} { \ text {d} t} \ end {bmatrix} = \ begin {bmatrix} - \ frac {R} {L} & - \ frac {1} {L} \\\ frac {1} {C} & 0 \ end {bmatrix} \ begin {bmatrix} i (t) \\ v_c (t) \ end {bmatrix} + \ begin {bmatrix} \ frac {1} {L} \\ 0 \ end {bmatrix} \ begin {bmatrix } v_i (t) \ end {bmatrix} $$
$$ Y = \ başla {bmatrix} 0 & 1 \ end {bmatrix} \ begin {bmatrix} i (t) \\ v_c (t) \ end {bmatrix} $$
Nerede,
$$ A = \ başla {bmatrix} - \ frac {R} {L} & - \ frac {1} {L} \\\ frac {1} {C} & 0 \ end {bmatrix}, \: B = \ begin {bmatrix} \ frac {1} {L} \\ 0 \ end {bmatrix}, \: C = \ begin {bmatrix} 0 & 1 \ end {bmatrix} \: ve \: D = \ begin {bmatrix } 0 \ end {bmatrix} $$
Transfer Fonksiyonundan Durum Uzay Modeli
Payda bulunan terimlerin türüne göre iki tür transfer işlevini düşünün.
- Payda sabit terimli transfer fonksiyonu.
- Numerator'daki 's' polinom fonksiyonuna sahip transfer fonksiyonu.
Payda sabit terime sahip transfer fonksiyonu
Bir sistemin aşağıdaki transfer işlevini düşünün
$$ \ frac {Y (s)} {U (s)} = \ frac {b_0} {s ^ n + a_ {n-1} s ^ {n-1} + ... + a_1s + a_0} $ $
Yukarıdaki denklemi yeniden düzenleyin
$$ (s ^ n + a_ {n-1} s ^ {n-1} + ... + a_0) Y (s) = b_0 U (s) $$
Her iki tarafta ters Laplace dönüşümü uygulayın.
$$ \ frac {\ text {d} ^ ny (t)} {\ text {d} t ^ n} + a_ {n-1} \ frac {\ text {d} ^ {n-1} y (t )} {\ text {d} t ^ {n-1}} + ... + a_1 \ frac {\ text {d} y (t)} {\ text {d} t} + a_0y (t) = b_0 u (t) $$
İzin Vermek
$$ y (t) = x_1 $$
$$ \ frac {\ text {d} y (t)} {\ text {d} t} = x_2 = \ dot {x} _1 $$
$$ \ frac {\ text {d} ^ 2y (t)} {\ text {d} t ^ 2} = x_3 = \ dot {x} _2 $$
$$. $$
$$. $$
$$. $$
$$ \ frac {\ text {d} ^ {n-1} y (t)} {\ text {d} t ^ {n-1}} = x_n = \ dot {x} _ {n-1} $ $
$$ \ frac {\ text {d} ^ ny (t)} {\ text {d} t ^ n} = \ dot {x} _n $$
ve $ u (t) = u $
Sonra,
$$ \ dot {x} _n + a_ {n-1} x_n + ... + a_1x_2 + a_0x_1 = b_0 u $$
Yukarıdaki denklemden aşağıdaki durum denklemini yazabiliriz.
$$ \ dot {x} _n = -a_0x_1-a_1x_2 -...- a_ {n-1} x_n + b_0 u $$
Çıktı denklemi -
$$ y (t) = y = x_1 $$
Durum uzayı modeli -
$ \ dot {X} = \ başla {bmatrix} \ dot {x} _1 \\\ dot {x} _2 \\\ vdots \\\ dot {x} _ {n-1} \\\ dot {x} _n \ end {bmatrix} $
$$ = \ begin {bmatrix} 0 & 1 & 0 & \ dotso & 0 & 0 \\ 0 & 0 & 1 & \ dotso & 0 & 0 \\\ vdots & \ vdots & \ vdots & \ dotso & \ vdots & \ vdots \\ 0 & 0 & 0 & \ dotso & 0 & 1 \\ - a_0 & -a_1 & -a_2 & \ dotso & -a_ {n-2} & -a_ {n-1} \ end {bmatrix } \ begin {bmatrix} x_1 \\ x_2 \\\ vdots \\ x_ {n-1} \\ x_n \ end {bmatrix} + \ begin {bmatrix} 0 \\ 0 \\\ vdots \\ 0 \\ b_0 \ end {bmatrix} \ begin {bmatrix} u \ end {bmatrix} $$
$$ Y = \ başla {bmatrix} 1 & 0 & \ dotso & 0 & 0 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \\\ vdots \\ x_ {n-1} \\ x_n \ end {bmatrix} $$
Burada, $ D = \ sol [0 \ sağ]. $
Misal
Transfer fonksiyonuna sahip sistem için durum uzayı modelini bulun.
$$ \ frac {Y (s)} {U (s)} = \ frac {1} {s ^ 2 + s + 1} $$
Yukarıdaki denklemi aşağıdaki gibi yeniden düzenleyin:
$$ (s ^ 2 + s + 1) Y (s) = U (s) $$
Her iki tarafa da ters Laplace dönüşümü uygulayın.
$$ \ frac {\ text {d} ^ 2y (t)} {\ text {d} t ^ 2} + \ frac {\ text {d} y (t)} {\ text {d} t} + y (t) = u (t) $$
İzin Vermek
$$ y (t) = x_1 $$
$$ \ frac {\ text {d} y (t)} {\ text {d} t} = x_2 = \ dot {x} _1 $$
ve $ u (t) = u $
O zaman durum denklemi
$$ \ dot {x} _2 = -x_1-x_2 + u $$
Çıktı denklemi
$$ y (t) = y = x_1 $$
Durum uzayı modeli
$$ \ dot {X} = \ begin {bmatrix} \ dot {x} _1 \\\ dot {x} _2 \ end {bmatrix} = \ begin {bmatrix} 0 & 1 \\ - 1 & -1 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix} + \ begin {bmatrix} 0 \\ 1 \ end {bmatrix} \ left [u \ right] $$
$$ Y = \ başla {bmatrix} 1 & 0 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix} $$
Payda 's' polinom fonksiyonuna sahip transfer fonksiyonu
Bir sistemin aşağıdaki transfer işlevini düşünün
$$ \ frac {Y (s)} {U (s)} = \ frac {b_n s ^ n + b_ {n-1} s ^ {n-1} + ... + b_1s + b_0} {s ^ n + a_ {n-1} s ^ {n-1} + ... + a_1 s + a_0} $$
$$ \ Rightarrow \ frac {Y (s)} {U (s)} = \ left (\ frac {1} {s ^ n + a_ {n-1} s ^ {n-1} + ... + a_1 s + a_0} \ sağ) (b_n s ^ n + b_ {n-1} s ^ {n-1} + ... + b_1s + b_0) $$
Yukarıdaki denklem, kademeli olan iki bloğun transfer fonksiyonlarının çarpımı şeklindedir.
$$ \ frac {Y (s)} {U (s)} = \ left (\ frac {V (s)} {U (s)} \ sağ) \ left (\ frac {Y (s)} {V (s)} \ sağ) $$
Buraya,
$$ \ frac {V (s)} {U (s)} = \ frac {1} {s ^ n + a_ {n-1} s ^ {n-1} + ... + a_1 s + a_0} $$
Yukarıdaki denklemi yeniden düzenleyin
$$ (s ^ n + a_ {n-1} s ^ {n-1} + ... + a_0) V (s) = U (s) $$
Her iki tarafa da ters Laplace dönüşümü uygulayın.
$$ \ frac {\ text {d} ^ nv (t)} {\ text {d} t ^ n} + a_ {n-1} \ frac {\ text {d} ^ {n-1} v (t )} {\ text {d} t ^ {n-1}} + ... + a_1 \ frac {\ text {d} v (t)} {\ text {d} t} + a_0v (t) = u (t) $$
İzin Vermek
$$ v (t) = x_1 $$
$$ \ frac {\ text {d} v ((t)} {\ text {d} t} = x_2 = \ dot {x} _1 $$
$$ \ frac {\ text {d} ^ 2v (t)} {\ text {d} t ^ 2} = x_3 = \ dot {x} _2 $$
$$. $$
$$. $$
$$. $$
$$ \ frac {\ text {d} ^ {n-1} v (t)} {\ text {d} t ^ {n-1}} = x_n = \ dot {x} _ {n-1} $ $
$$ \ frac {\ text {d} ^ nv (t)} {\ text {d} t ^ n} = \ dot {x} _n $$
ve $ u (t) = u $
O zaman durum denklemi
$$ \ dot {x} _n = -a_0x_1-a_1x_2 -...- a_ {n-1} x_n + u $$
Düşünmek,
$$ \ frac {Y (s)} {V (s)} = b_ns ^ n + b_ {n-1} s ^ {n-1} + ... + b_1s + b_0 $$
Yukarıdaki denklemi yeniden düzenleyin
$$ Y (ler) = (b_ns ^ n + b_ {n-1} s ^ {n-1} + ... + b_1s + b_0) V (s) $$
Her iki tarafa da ters Laplace dönüşümü uygulayın.
$$ y (t) = b_n \ frac {\ text {d} ^ nv (t)} {\ text {d} t ^ n} + b_ {n-1} \ frac {\ text {d} ^ {n -1} v (t)} {\ text {d} t ^ {n-1}} + ... + b_1 \ frac {\ text {d} v (t)} {\ text {d} t} + b_0v (t) $$
Yukarıdaki denklemde durum değişkenlerini ve $ y (t) = y $ 'ı değiştirerek, çıkış denklemini şu şekilde alacaktır:
$$ y = b_n \ dot {x} _n + b_ {n-1} x_n + ... + b_1x_2 + b_0x_1 $$
Yukarıdaki denklemde, $ \ dot {x} _n $ değerini değiştirin.
$$ y = b_n (-a_0x_1-a_1x_2 -...- a_ {n-1} x_n + u) + b_ {n-1} x_n + ... + b_1x_2 + b_0x_1 $$
$$ y = (b_0-b_na_0) x_1 + (b_1-b_na_1) x_2 + ... + (b_ {n-1} -b_na_ {n-1}) x_n + b_n u $$
Durum uzayı modeli
$ \ dot {X} = \ başla {bmatrix} \ dot {x} _1 \\\ dot {x} _2 \\\ vdots \\\ dot {x} _ {n-1} \\\ dot {x} _n \ end {bmatrix} $
$$ = \ begin {bmatrix} 0 & 1 & 0 & \ dotso & 0 & 0 \\ 0 & 0 & 1 & \ dotso & 0 & 0 \\\ vdots & \ vdots & \ vdots & \ dotso & \ vdots & \ vdots \\ 0 & 0 & 0 & \ dotso & 0 & 1 \\ - a_0 & -a_1 & -a_2 & \ dotso & -a_ {n-2} & -a_ {n-1} \ end {bmatrix } \ begin {bmatrix} x_1 \\ x_2 \\\ vdots \\ x_ {n-1} \\ x_n \ end {bmatrix} + \ begin {bmatrix} 0 \\ 0 \\\ vdots \\ 0 \\ b_0 \ end {bmatrix} \ begin {bmatrix} u \ end {bmatrix} $$
$$ Y = [b_0-b_na_0 \ quad b_1-b_na_1 \ quad ... \ quad b_ {n-2} -b_na_ {n-2} \ quad b_ {n-1} -b_na_ {n-1}] \ başlayın {bmatrix} x_1 \\ x_2 \\\ vdots \\ x_ {n-1} \\ x_n \ end {bmatrix} $$
$ B_n = 0 $ ise, o zaman,
$$ Y = [b_0 \ quad b_1 \ quad ... \ quad b_ {n-2} \ quad b_ {n-1}] \ başla {bmatrix} x_1 \\ x_2 \\\ vdots \\ x_ {n- 1} \\ x_n \ end {bmatrix} $$
Önceki bölümde diferansiyel denklem ve transfer fonksiyonundan durum uzayı modelinin nasıl elde edileceğini öğrendik. Bu bölümde, durum uzayı modelinden transfer fonksiyonunun nasıl elde edileceğini tartışalım.
Durum Uzay Modelinden Transfer Fonksiyonu
Doğrusal Zamanla Değişmeyen (LTI) bir sistemin durum uzay modelinin -
$$ \ dot {X} = AX + BU $$
$$ Y = CX + DU $$
Durum denkleminin her iki tarafına da Laplace Dönüşümünü uygulayın.
$$ sX (ler) = AX (ler) + BU (s) $$
$$ \ Rightarrow (sI-A) X (s) = BU (s) $$
$$ \ Rightarrow X (s) = (sI-A) ^ {- 1} BU (s) $$
Çıktı denkleminin her iki tarafına da Laplace Dönüşümü uygulayın.
$$ Y (ler) = CX (ler) + DU (lar) $$
İkame, yukarıdaki denklemde X (s) değeri.
$$ \ Rightarrow Y (s) = C (sI-A) ^ {- 1} BU (s) + DU (s) $$
$$ \ Rightarrow Y (s) = [C (sI-A) ^ {- 1} B + D] U (s) $$
$$ \ Rightarrow \ frac {Y (s)} {U (s)} = C (sI-A) ^ {- 1} B + D $$
Yukarıdaki denklem, sistemin transfer fonksiyonunu temsil eder. Dolayısıyla, durum uzayı modelinde gösterilen sistem için bu formülü kullanarak sistemin transfer fonksiyonunu hesaplayabiliriz.
Note - $ D = [0] $ olduğunda, transfer işlevi
$$ \ frac {Y (s)} {U (s)} = C (sI-A) ^ {- 1} B $$
Example
Durum uzayı modelinde temsil edilen sistemin transfer fonksiyonunu şu şekilde hesaplayalım:
$$ \ dot {X} = \ begin {bmatrix} \ dot {x} _1 \\\ dot {x} _2 \ end {bmatrix} = \ begin {bmatrix} -1 & -1 \\ 1 & 0 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix} + \ begin {bmatrix} 1 \\ 0 \ end {bmatrix} [u] $$
$$ Y = \ başla {bmatrix} 0 & 1 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix} $$
Buraya,
$$ A = \ begin {bmatrix} -1 & -1 \\ 1 & 0 \ end {bmatrix}, \ quad B = \ begin {bmatrix} 1 \\ 0 \ end {bmatrix}, \ quad C = \ begin {bmatrix} 0 ve 1 \ end {bmatrix} \ quad ve \ quad D = [0] $$
$ D = [0] $ - olduğunda transfer fonksiyonu formülü
$$ \ frac {Y (s)} {U (s)} = C (sI-A) ^ {- 1} B $$
Yukarıdaki denklemde A, B ve C matrislerini ikame edin.
$$ \ frac {Y (s)} {U (s)} = \ begin {bmatrix} 0 & 1 \ end {bmatrix} \ begin {bmatrix} s + 1 & 1 \\ - 1 & s \ end {bmatrix } ^ {- 1} \ başla {bmatrix} 1 \\ 0 \ end {bmatrix} $$
$$ \ Rightarrow \ frac {Y (s)} {U (s)} = \ begin {bmatrix} 0 & 1 \ end {bmatrix} \ frac {\ begin {bmatrix} s & -1 \\ 1 & s + 1 \ end {bmatrix}} {(s + 1) s-1 (-1)} \ begin {bmatrix} 1 \\ 0 \ end {bmatrix} $$
$$ \ Rightarrow \ frac {Y (s)} {U (s)} = \ frac {\ begin {bmatrix} 0 & 1 \ end {bmatrix} \ begin {bmatrix} s \\ 1 \ end {bmatrix}} {s ^ 2 + s + 1} = \ frac {1} {s ^ 2 + s + 1} $$
Bu nedenle, verilen durum uzayı modeli için sistemin transfer işlevi
$$ \ frac {Y (s)} {U (s)} = \ frac {1} {s ^ 2 + s + 1} $$
Durum Geçiş Matrisi ve Özellikleri
Sistem başlangıç koşullarına sahipse, bir çıktı üretecektir. Bu çıktı, girdi olmadığında bile mevcut olduğundan, denirzero input response$ x_ {ZIR} (t) $. Matematiksel olarak şöyle yazabiliriz:
$$ x_ {ZIR} (t) = e ^ {At} X (0) = L ^ {- 1} \ left \ {\ left [sI-A \ sağ] ^ {- 1} X (0) \ sağ \} $$
Yukarıdaki ilişkiden $ \ phi (t) $ durum geçiş matrisini şu şekilde yazabiliriz:
$$ \ phi (t) = e ^ {At} = L ^ {- 1} [sI-A] ^ {- 1} $$
Dolayısıyla, sıfır girdi cevabı $ \ phi (t) $ durum geçiş matrisi ile başlangıç koşulları matrisi çarpılarak elde edilebilir.
Durum geçiş matrisinin özellikleri aşağıdadır.
$ T = 0 $ ise, durum geçiş matrisi bir Özdeşlik matrisine eşit olacaktır.
$$ \ phi (0) = I $$
Durum geçiş matrisinin tersi, sadece 't'yi' -t 'ile değiştirerek durum geçiş matrisininki ile aynı olacaktır.
$$ \ phi ^ {- 1} (t) = \ phi (−t) $$
$ T = t_1 + t_2 ise$ , then the corresponding state transition matrix is equal to the multiplication of the two state transition matrices at $t = t_1$ and $t = t_2 $.
$$ \ phi (t_1 + t_2) = \ phi (t_1) \ phi (t_2) $$
Kontrol Edilebilirlik ve Gözlenebilirlik
Şimdi kontrol sisteminin kontrol edilebilirliğini ve gözlemlenebilirliğini tek tek tartışalım.
Kontrol edilebilirlik
Bir kontrol sistemi olduğu söyleniyor controllable kontrol sisteminin başlangıç durumları, sınırlı bir süre içinde kontrollü bir girdi ile istenen diğer bazı durumlara aktarılırsa (değiştirilirse).
Bir kontrol sisteminin kontrol edilebilirliğini kullanarak kontrol edebiliriz Kalman’s test.
$ Q_c $ matrisini aşağıdaki forma yazın.
$$ Q_c = \ left [B \ quad AB \ quad A ^ 2B \ quad ... \ quad A ^ {n-1} B \ right] $$
$ Q_c $ matrisinin determinantını bulun ve sıfıra eşit değilse, kontrol sistemi kontrol edilebilir.
Gözlenebilirlik
Bir kontrol sistemi olduğu söyleniyor observable Kontrol sisteminin başlangıç durumlarını, çıktıları sınırlı bir süre içinde gözlemleyerek belirleyebiliyorsa.
Kullanarak bir kontrol sisteminin gözlenebilirliğini kontrol edebiliriz Kalman’s test.
$ Q_o $ matrisini aşağıdaki biçimde yazın.
$$ Q_o = \ left [C ^ T \ quad A ^ TC ^ T \ quad (A ^ T) ^ 2C ^ T \ quad ... \ quad (A ^ T) ^ {n-1} C ^ T \ sağ] $$
$ Q_o $ matrisinin determinantını bulun ve sıfıra eşit değilse, o zaman kontrol sistemi gözlemlenebilir.
Example
Durum uzayı modelinde şu şekilde temsil edilen bir kontrol sisteminin kontrol edilebilirliğini ve gözlemlenebilirliğini doğrulayalım:
$$ \ dot {x} = \ begin {bmatrix} \ dot {x} _1 \\\ dot {x} _2 \ end {bmatrix} = \ begin {bmatrix} -1 & -1 \\ 1 & 0 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix} + \ begin {bmatrix} 1 \\ 0 \ end {bmatrix} [u] $$
$$ Y = \ başla {bmatrix} 0 & 1 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix} $$
Buraya,
$$ A = \ begin {bmatrix} -1 & -1 \\ 1 & 0 \ end {bmatrix}, \ quad B = \ begin {bmatrix} 1 \\ 0 \ end {bmatrix}, \ quad \ begin {bmatrix } 0 ve 1 \ end {bmatrix}, D = [0] \ quad ve \ quad n = 2 $$
$ N = 2 için$, the matrix $Q_c $ olacak
$$ Q_c = \ sol [B \ quad AB \ sağ] $$
A ve B matrislerinin çarpımını şu şekilde alacağız:
$$ AB = \ başlangıç {bmatrix} -1 \\ 1 \ end {bmatrix} $$
$$ \ Rightarrow Q_c = \ begin {bmatrix} 1 & -1 \\ 0 & 1 \ end {bmatrix} $$
$$ | Q_c | = 1 \ neq 0 $$
$ Q_c $ matrisinin determinantı sıfıra eşit olmadığından, verilen kontrol sistemi kontrol edilebilir.
$ N = 2 için$, the matrix $Q_o $ - olacak
$$ Q_o = \ sol [C ^ T \ quad A ^ TC ^ T \ sağ] $$
Buraya,
$$ A ^ T = \ begin {bmatrix} -1 & 1 \\ - 1 & 0 \ end {bmatrix} \ quad ve \ quad C ^ T = \ begin {bmatrix} 0 \\ 1 \ end {bmatrix} $ $
$ A ^ T matrislerinin çarpımını alacağız$ and $C ^ T $ as
$$ A ^ TC ^ T = \ başla {bmatrix} 1 \\ 0 \ end {bmatrix} $$
$$ \ Rightarrow Q_o = \ begin {bmatrix} 0 & 1 \\ 1 & 0 \ end {bmatrix} $$
$$ \ Rightarrow | Q_o | = -1 \ quad \ neq 0 $$
$ Q_o $ matrisinin determinantı sıfıra eşit olmadığından, verilen kontrol sistemi gözlemlenebilir.
Bu nedenle, verilen kontrol sistemi hem kontrol edilebilir hem de gözlemlenebilir.