Kontrol Sistemleri - Blok Şemalar
Blok diyagramlar tek bir bloktan veya blokların bir kombinasyonundan oluşur. Bunlar, kontrol sistemlerini resimli biçimde temsil etmek için kullanılır.
Blok Diyagramın Temel Öğeleri
Bir blok diyagramın temel öğeleri bir blok, toplama noktası ve kalkış noktasıdır. Bu elemanları tanımlamak için aşağıdaki şekilde gösterildiği gibi bir kapalı döngü kontrol sisteminin blok diyagramını ele alalım.

Yukarıdaki blok diyagram, G (s) ve H (s) transfer fonksiyonlarına sahip iki bloktan oluşur. Aynı zamanda bir toplama noktası ve bir kalkış noktası var. Oklar, sinyallerin akış yönünü gösterir. Şimdi bu unsurları tek tek tartışalım.
Blok
Bir bileşenin transfer fonksiyonu bir blok ile temsil edilir. Blok tek girişli ve tek çıkışlıdır.
Aşağıdaki şekil, giriş X (s), çıkış Y (s) ve transfer fonksiyonu G (s) olan bir bloğu göstermektedir.

Transfer İşlevi, $ G (s) = \ frac {Y (s)} {X (s)} $
$$ \ Rightarrow Y (s) = G (s) X (s) $$
Bloğun çıkışı, bloğun transfer fonksiyonunun girdi ile çarpılmasıyla elde edilir.
Toplama Noktası
Toplama noktası, içinde çarpı işareti (X) olan bir daire ile temsil edilir. İki veya daha fazla girişi ve tek çıkışı vardır. Girişlerin cebirsel toplamını üretir. Ayrıca, girişlerin polaritesine bağlı olarak girişlerin toplama veya çıkarma veya toplama ve çıkarma kombinasyonunu gerçekleştirir. Gelin bu üç işlemi tek tek görelim.
Aşağıdaki şekil iki girişli (A, B) ve bir çıkışlı (Y) toplama noktasını göstermektedir. Burada, A ve B girişlerinin pozitif bir işareti vardır. Böylece, toplama noktası Y çıktısını üretir.sum of A and B.
yani, Y = A + B.

Aşağıdaki şekil iki girişli (A, B) ve bir çıkışlı (Y) toplama noktasını göstermektedir. Burada, A ve B girişleri zıt işaretlere sahiptir, yani A pozitif işarete ve B negatif işarete sahiptir. Böylece, toplama noktası çıktıyı üretirY olarak difference of A and B.
Y = A + (-B) = A - B.

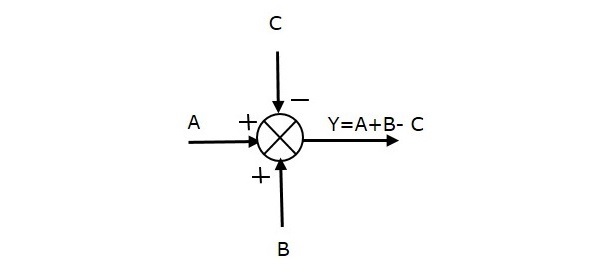
Aşağıdaki şekil, üç giriş (A, B, C) ve bir çıkış (Y) ile toplama noktasını göstermektedir. Burada, A ve B girişleri pozitif işaretlere sahip ve C, negatif işarete sahip. Böylece, toplama noktası çıktıyı üretirY gibi
Y = A + B + (−C) = A + B - C.
Kalkış Noktası
Kalkış noktası, aynı giriş sinyalinin birden fazla daldan geçirilebildiği bir noktadır. Bu, kalkış noktası yardımıyla, aynı girdiyi bir veya daha fazla bloğa, toplama noktalarına uygulayabileceğimiz anlamına gelir.
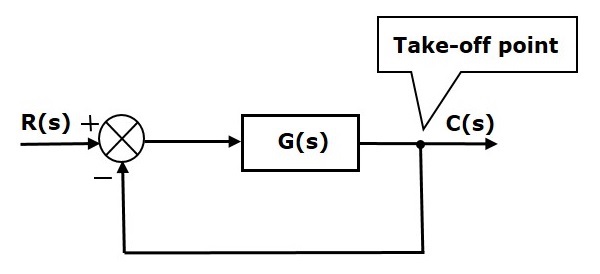
Aşağıdaki şekilde, kalkış noktası aynı girişi R (s) iki bloğa daha bağlamak için kullanılır.

Aşağıdaki şekilde, kalkış noktası, girişlerden biri olarak C (ler) çıkışını toplama noktasına bağlamak için kullanılır.
Elektrik Sistemlerinin Blok Şema Gösterimi
Bu bölümde bir elektrik sistemini blok diyagramla gösterelim. Elektrik sistemleri temel olarak üç temel unsur içerir -resistor, inductor and capacitor.
Aşağıdaki şekilde gösterildiği gibi bir dizi RLC devresini düşünün. Burada, V i (t) ve V o (t) giriş ve çıkış voltajlarıdır. Devreden geçen akım ben (t) olsun. Bu devre zaman etki alanı içindedir.

Laplace dönüşümünü bu devreye uygulayarak devreyi s-alanında alacaksınız. Devre aşağıdaki şekilde gösterildiği gibidir.
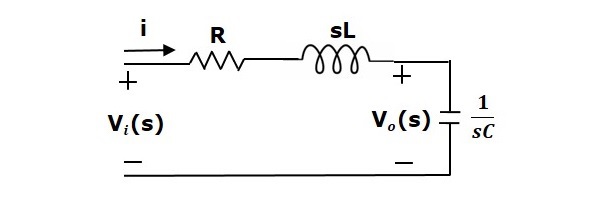
Yukarıdaki devreden yazabiliriz
$$ I (s) = \ frac {V_i (s) -V_o (s)} {R + sL} $$
$ \ Rightarrow I (s) = \ left \ {\ frac {1} {R + sL} \ sağ \} \ left \ {V_i (s) -V_o (s) \ sağ \} $ (Equation 1)
$ V_o (s) = \ sol (\ frac {1} {sC} \ sağ) I (s) $ (Equation 2)
Şimdi bu iki denklem için blok diyagramlarını ayrı ayrı çizelim. Ve daha sonra, RLC Devresi (s-alanı) serisinin genel blok diyagramını elde etmek için bu blok diyagramlarını doğru şekilde birleştirin.
Denklem 1, transfer fonksiyonu $ \ frac {1} {R + sL} $ olan bir blok ile uygulanabilir. Bu bloğun girdisi ve çıktısı $ \ left \ {V_i (s) -V_o (s) \ right \} $ ve $ I (s) $ şeklindedir. $ \ Left \ {V_i (s) -V_o (s) \ right \} $ elde etmek için bir toplama noktasına ihtiyacımız var. Denklem 1'in blok diyagramı aşağıdaki şekilde gösterilmektedir.

Denklem 2, transfer fonksiyonu $ \ frac {1} {sC} $ olan bir blok ile uygulanabilir. Bu bloğun girdisi ve çıktısı $ I (s) $ ve $ V_o (s) $ 'dır. Denklem 2'nin blok diyagramı aşağıdaki şekilde gösterilmektedir.

RLC Devresi (s-alanı) serisinin genel blok diyagramı aşağıdaki şekilde gösterilmektedir.

Benzer şekilde, çizebilirsiniz block diagram herhangi bir elektrik devresinin veya sisteminin sadece bu basit prosedürü izleyerek.
Laplace dönüşümünü uygulayarak zaman alanı elektrik devresini bir s-alanı elektrik devresine dönüştürün.
Tüm seri branş elemanlarından geçen akım ve tüm şönt branşlarındaki voltaj için denklemleri yazın.
Yukarıdaki denklemlerin tümü için blok diyagramlarını ayrı ayrı çizin.
Elektrik devresinin (s-alanı) genel blok diyagramını elde etmek için tüm bu blok diyagramlarını doğru şekilde birleştirin.