Analoge Kommunikation - FM-Modulatoren
Lassen Sie uns in diesem Kapitel die Modulatoren diskutieren, die NBFM- und WBFM-Wellen erzeugen. Lassen Sie uns zunächst über die Erzeugung von NBFM diskutieren.
Erzeugung von NBFM
Wir wissen, dass die Standardgleichung der FM-Welle lautet
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt \ right) $$
$ \ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) \ cos \ left (2 \ pi k_f \ int m \ left (t \ right) dt \ right) - $
$ A_c \ sin \ left (2 \ pi f_ct \ right) \ sin \ left (2 \ pi k_f \ int m \ left (t \ right) dt \ right) $
Für NBFM
$$ \ left | 2 \ pi k_f \ int m \ left (t \ right) dt \ right | << 1 $$
Wir wissen, dass $ \ cos \ theta \ ungefähr 1 $ und $ \ sin \ theta \ ungefähr 1 $ ist, wenn $ \ theta $ sehr klein ist.
Durch Verwendung der obigen Beziehungen erhalten wir die NBFM equation wie
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) -A_c \ sin \ left (2 \ pi f_ct \ right) 2 \ pi k_f \ int m \ left (t \ rechts) dt $$
Das Blockschaltbild des NBFM-Modulators ist in der folgenden Abbildung dargestellt.
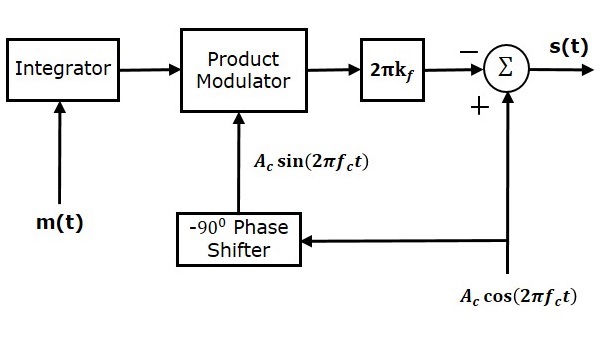
Hier wird der Integrator verwendet, um das Modulationssignal $ m \ left (t \ right) $ zu integrieren. Das Trägersignal $ A_c \ cos \ left (2 \ pi f_ct \ right) $ ist die um $ -90 ^ 0 $ verschobene Phase, um mit Hilfe von $ A_c \ sin \ left (2 \ pi f_ct \ right) $ zu erhalten $ -90 ^ 0 $ Phasenschieber. Der Produktmodulator hat zwei Eingänge $ \ int m \ left (t \ right) dt $ und $ A_c \ sin \ left (2 \ pi f_ct \ right) $. Es wird eine Ausgabe erzeugt, die das Produkt dieser beiden Eingaben ist.
Dies wird weiter mit $ 2 \ pi k_f $ multipliziert, indem ein Block $ 2 \ pi k_f $ in den Vorwärtspfad gesetzt wird. Der Sommerblock hat zwei Eingänge, die nichts anderes als die beiden Terme der NBFM-Gleichung sind. Positive und negative Vorzeichen werden für das Trägersignal und den anderen Term am Eingang des Sommerblocks zugewiesen. Schließlich erzeugt der Sommerblock eine NBFM-Welle.
Erzeugung von WBFM
Die folgenden zwei Methoden erzeugen eine WBFM-Welle.
- Direkte Methode
- Indirekte Methode
Direkte Methode
Diese Methode wird als direkte Methode bezeichnet, da wir direkt eine Breitband-FM-Welle erzeugen. Bei diesem Verfahren wird ein spannungsgesteuerter Oszillator (VCO) verwendet, um WBFM zu erzeugen. VCO erzeugt ein Ausgangssignal, dessen Frequenz proportional zur Eingangssignalspannung ist. Dies ähnelt der Definition der FM-Welle. Das Blockschaltbild der Erzeugung der WBFM-Welle ist in der folgenden Abbildung dargestellt.

Hier wird das Modulationssignal $ m \ left (t \ right) $ als Eingang des Voltage Controlled Oscillator (VCO) angelegt. VCO erzeugt eine Ausgabe, die nichts anderes als das WBFM ist.
$$ f_i \: \ alpha \: m \ left (t \ right) $$
$$ \ Rightarrow f_i = f_c + k_fm \ left (t \ right) $$
Wo,
$ f_i $ ist die momentane Frequenz der WBFM-Welle.
Indirekte Methode
Diese Methode wird als indirekte Methode bezeichnet, da wir indirekt eine Breitband-FM-Welle erzeugen. Dies bedeutet, dass wir zuerst eine NBFM-Welle erzeugen und dann mit Hilfe von Frequenzvervielfachern eine WBFM-Welle erhalten. Das Blockschaltbild der Erzeugung der WBFM-Welle ist in der folgenden Abbildung dargestellt.

Dieses Blockdiagramm enthält hauptsächlich zwei Stufen. In der ersten Stufe wird die NBFM-Welle unter Verwendung eines NBFM-Modulators erzeugt. Wir haben das Blockdiagramm des NBFM-Modulators am Anfang dieses Kapitels gesehen. Wir wissen, dass der Modulationsindex der NBFM-Welle kleiner als eins ist. Wählen Sie daher den Frequenzvervielfacherwert richtig aus, um den erforderlichen Modulationsindex (größer als eins) der FM-Welle zu erhalten.
Frequency multiplierist ein nichtlineares Gerät, das ein Ausgangssignal erzeugt, dessen Frequenz das n-fache der Eingangssignalfrequenz beträgt. Wobei 'n' der Multiplikationsfaktor ist.
Wenn eine NBFM-Welle, deren Modulationsindex $ \ beta $ kleiner als 1 ist, als Eingang des Frequenzvervielfachers angewendet wird, erzeugt der Frequenzvervielfacher ein Ausgangssignal, dessen Modulationsindex 'n' mal $ \ beta $ und die Frequenz auch 'n' ist 'mal die Frequenz der WBFM-Welle.
Manchmal benötigen wir mehrere Stufen eines Frequenzvervielfachers und von Mischern, um die Frequenzabweichung und den Modulationsindex der FM-Welle zu erhöhen.