Analoge Kommunikation - Abtastung
Bisher haben wir über Dauerstrichmodulation diskutiert. Wir werden im nächsten Kapitel über Pulsmodulation diskutieren. Diese Pulsmodulationstechniken befassen sich mit diskreten Signalen. Lassen Sie uns nun sehen, wie ein kontinuierliches Zeitsignal in ein diskretes umgewandelt wird.
Der Prozess der Umwandlung kontinuierlicher Zeitsignale in äquivalente diskrete Zeitsignale kann als bezeichnet werden Sampling. Ein bestimmter Zeitpunkt der Daten wird während des Abtastvorgangs kontinuierlich abgetastet.
Die folgende Abbildung zeigt ein zeitkontinuierliches Signal x(t) und das entsprechende abgetastete Signal xs(t). Wannx(t) wird mit einer periodischen Impulsfolge multipliziert, dem abgetasteten Signal xs(t) erhalten wird.

EIN sampling signal ist eine periodische Folge von Impulsen mit einer Einheitsamplitude, die in gleichen Zeitintervallen $ T_s $ abgetastet wird und als bezeichnet wird sampling time. Diese Daten werden zu den Zeitpunkten $ T_s $ übertragen und das Trägersignal wird zum verbleibenden Zeitpunkt übertragen.
Abtastrate
Um die Signale zu diskretisieren, sollte der Abstand zwischen den Abtastwerten festgelegt werden. Diese Lücke kann als Abtastperiode $ T_s $ bezeichnet werden. Der Kehrwert der Abtastperiode ist bekannt alssampling frequency oder sampling rate $f_s$.
Mathematisch können wir es schreiben als
$$ f_s = \ frac {1} {T_s} $$
Wo,
$ f_s $ ist die Abtastfrequenz oder die Abtastrate
$ T_s $ ist die Abtastperiode
Abtasttheorem
Die Abtastrate sollte so sein, dass die Daten im Nachrichtensignal weder verloren gehen noch überlappen. Dassampling theorem heißt es: „Ein Signal kann exakt reproduziert werden, wenn es mit der Rate $ f_s $ abgetastet wird, die größer oder gleich der doppelten maximalen Frequenz des gegebenen Signals ist W. ”
Mathematisch können wir es schreiben als
$$ f_s \ geq 2W $$
Wo,
$ f_s $ ist die Abtastrate
$ W $ ist die höchste Frequenz des gegebenen Signals
Wenn die Abtastrate gleich der doppelten maximalen Frequenz des gegebenen Signals W ist, wird sie als bezeichnet Nyquist rate.
Der Abtastsatz, der auch als bezeichnet wird Nyquist theoremliefert die Theorie einer ausreichenden Abtastrate in Bezug auf die Bandbreite für die Klasse von Funktionen, die bandbegrenzt sind.
Für zeitkontinuierliches Signal x(t), die im Frequenzbereich bandbegrenzt ist, ist wie in der folgenden Abbildung dargestellt dargestellt.

Wenn das Signal über der Nyquist-Rate abgetastet wird, kann das ursprüngliche Signal wiederhergestellt werden. Die folgende Abbildung erläutert ein Signal, wenn es mit einer höheren Rate als abgetastet wird2w im Frequenzbereich.
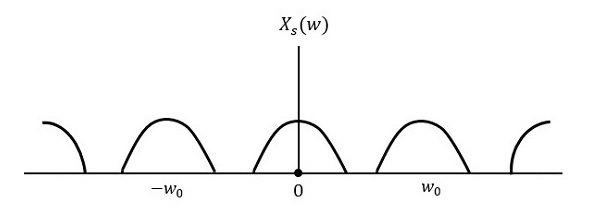
Wenn dasselbe Signal mit einer Rate von weniger als abgetastet wird 2wdann würde das abgetastete Signal wie in der folgenden Abbildung aussehen.

Wir können anhand des obigen Musters beobachten, dass es zu einer Überlappung von Informationen kommt, was zu Verwechslungen und Informationsverlust führt. Dieses unerwünschte Phänomen des Überlappens wird als bezeichnetAliasing.
Aliasing kann als "das Phänomen einer Hochfrequenzkomponente im Spektrum eines Signals bezeichnet werden, das die Identität einer Niederfrequenzkomponente im Spektrum seiner abgetasteten Version annimmt".
Daher wird die Abtastrate des Signals als Nyquist-Rate gewählt. Wenn die Abtastrate gleich der doppelten höchsten Frequenz des gegebenen Signals istWdann würde das abgetastete Signal wie in der folgenden Abbildung aussehen.

In diesem Fall kann das Signal ohne Verlust wiederhergestellt werden. Daher ist dies eine gute Abtastrate.