Boolsche Algebra
Die Boolesche Algebra wird verwendet, um die digitalen (logischen) Schaltungen zu analysieren und zu vereinfachen. Es werden nur die Binärzahlen dh 0 und 1 verwendet. Es wird auch als bezeichnetBinary Algebra oder logical Algebra. Die Boolesche Algebra wurde von erfundenGeorge Boole im Jahre 1854.
Regel in der Booleschen Algebra
Im Folgenden sind die wichtigen Regeln aufgeführt, die in der Booleschen Algebra verwendet werden.
Die verwendete Variable kann nur zwei Werte haben. Binär 1 für HOCH und Binär 0 für NIEDRIG.
Das Komplement einer Variablen wird durch einen Überstrich (-) dargestellt. Somit wird das Komplement der Variablen B dargestellt als
. Wenn also B = 0, dann = 1 und B = 1, dann
= 1 und B = 1, dann = 0.
= 0.
Die ODER-Verknüpfung der Variablen wird durch ein Pluszeichen (+) zwischen ihnen dargestellt. Zum Beispiel wird die OR-Verknüpfung von A, B, C als A + B + C dargestellt.
Die logische UND-Verknüpfung der zwei oder mehr Variablen wird durch Schreiben eines Punkts zwischen ihnen wie ABC dargestellt. Manchmal kann der Punkt wie ABC weggelassen werden.
Boolesche Gesetze
Es gibt sechs Arten von Booleschen Gesetzen.
Kommutativgesetz
Jede binäre Operation, die den folgenden Ausdruck erfüllt, wird als kommutative Operation bezeichnet.

Das kommutative Gesetz besagt, dass das Ändern der Reihenfolge der Variablen keine Auswirkung auf den Ausgang einer Logikschaltung hat.
Assoziatives Recht
Dieses Gesetz besagt, dass die Reihenfolge, in der die logischen Operationen ausgeführt werden, irrelevant ist, da ihre Wirkung dieselbe ist.
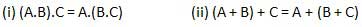
Verteilungsrecht
Das Verteilungsgesetz legt die folgende Bedingung fest.
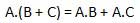
UND Gesetz
Diese Gesetze verwenden die UND-Operation. Deshalb heißen sie alsAND Rechtsvorschriften.
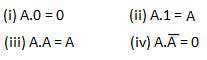
ODER Gesetz
Diese Gesetze verwenden die OP-Operation. Deshalb heißen sie alsOR Rechtsvorschriften.
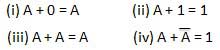
INVERSIONSGESETZ
Dieses Gesetz verwendet die NOT-Operation. Das Inversionsgesetz besagt, dass die doppelte Inversion einer Variablen zur ursprünglichen Variablen selbst führt.
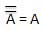
Wichtige boolesche Theoreme
Es folgen einige wichtige boolesche Theoreme.
| Boolesche Funktion / Theoreme | Beschreibung |
|---|---|
Boolesche Funktionen |
Boolesche Funktionen und Ausdrücke, K-Map- und NAND-Gates-Realisierung |
De Morgans Theoreme |
Satz 1 von De Morgan und Satz 2 |