Hexadezimale Arithmetik
Hexadezimalzahlensystem
Es folgen die Merkmale eines Hexadezimalzahlensystems.
Verwendet 10 Ziffern und 6 Buchstaben, 0,1,2,3,4,5,6,7,8,9, A, B, C, D, E, F.
Buchstaben stehen für Zahlen ab 10. A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
Wird auch als Basis-16-Zahlensystem bezeichnet.
Jede Position in einer Hexadezimalzahl repräsentiert eine 0-Potenz der Basis (16). Beispiel - 16 0
Die letzte Position in einer Hexadezimalzahl repräsentiert eine x-Potenz der Basis (16). Beispiel - 16 x wobei x die letzte Position darstellt - 1.
Beispiel
Hexadezimalzahl - 19FDE 16
Dezimaläquivalent berechnen -
| Schritt | Hexadezimalzahl | Dezimalzahl |
|---|---|---|
| Schritt 1 | 19FDE 16 | ((1 × 16 4 ) + (9 × 16 3 ) + (F × 16 2 ) + (D × 16 1 ) + (E × 16 0 )) 10 |
| Schritt 2 | 19FDE 16 | ((1 × 16 4 ) + (9 × 16 3 ) + (15 × 16 2 ) + (13 × 16 1 ) + (14 × 16 0 )) 10 |
| Schritt 3 | 19FDE 16 | (65536 + 36864 + 3840 + 208 + 14) 10 |
| Schritt 4 | 19FDE 16 | 106462 10 |
Note −19FDE 16 wird normalerweise als 19FDE geschrieben.
Hexadezimale Addition
Das Befolgen der hexadezimalen Additionstabelle hilft Ihnen bei der Handhabung der hexadezimalen Addition.
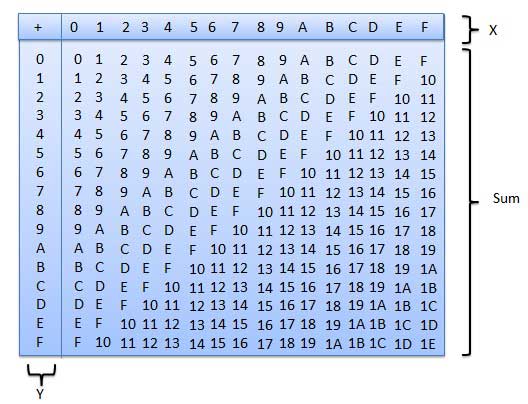
Befolgen Sie zur Verwendung dieser Tabelle einfach die Anweisungen in diesem Beispiel - Fügen Sie A 16 und 5 16 hinzu . Suchen Sie A in der X-Spalte und dann die 5 in der Y-Spalte. Der Punkt im Summenbereich, an dem sich diese beiden Spalten schneiden, ist die Summe zweier Zahlen.
A16 + 516 = F16.Beispiel - Addition
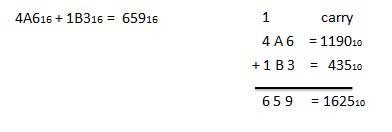
Hexadezimale Subtraktion
Die Subtraktion von Hexadezimalzahlen folgt den gleichen Regeln wie die Subtraktion von Zahlen in jedem anderen Zahlensystem. Die einzige Variation ist die geliehene Anzahl. Im Dezimalsystem leihen Sie sich eine Gruppe von 10 10 aus . Im Binärsystem leihen Sie sich eine Gruppe von 2 10 aus . Im Hexadezimalsystem leihen Sie sich eine Gruppe von 16 10 aus .
Beispiel - Subtraktion
