Diskrete Mathematik - Gruppentheorie
Halbgruppe
Eine endliche oder unendliche Menge $ 'S' $ mit einer binären Operation $ '\ omicron' $ (Komposition) heißt Halbgruppe, wenn sie zwei Bedingungen gleichzeitig erfüllt -
Closure - Für jedes Paar $ (a, b) \ in S muss \ :( a \ omicron b) $ in der Menge $ S $ vorhanden sein.
Associative - Für jedes Element $ a, b, c \ in S muss (a \ omicron b) \ omicron c = a \ omicron (b \ omicron c) $ gelten.
Beispiel
Die Menge der positiven ganzen Zahlen (ohne Null) mit Additionsoperation ist eine Halbgruppe. Zum Beispiel $ S = \ lbrace 1, 2, 3, \ dots \ rbrace $
Hier gilt die Closure-Eigenschaft wie für jedes Paar $ (a, b) \ in S, (a + b) $ ist in der Menge S vorhanden. Zum Beispiel ist $ 1 + 2 = 3 \ in S] $
Assoziative Eigenschaft gilt auch für jedes Element $ a, b, c \ in S, (a + b) + c = a + (b + c) $. Zum Beispiel ist $ (1 + 2) + 3 = 1 + (2 + 3) = 5 $
Monoid
Ein Monoid ist eine Halbgruppe mit einem Identitätselement. Das Identitätselement (bezeichnet mit $ e $ oder E) einer Menge S ist ein Element, so dass $ (a \ omicron e) = a $ für jedes Element $ a \ in S $ ist. Ein Identitätselement wird auch als bezeichnetunit element. Ein Monoid hat also drei Eigenschaften gleichzeitig -Closure, Associative, Identity element.
Beispiel
Die Menge der positiven ganzen Zahlen (ohne Null) mit Multiplikationsoperation ist ein Monoid. $ S = \ lbrace 1, 2, 3, \ dots \ rbrace $
Hier gilt die Closure-Eigenschaft wie für jedes Paar $ (a, b) \ in S, (a \ times b) $ ist in der Menge S vorhanden. [Zum Beispiel $ 1 \ times 2 = 2 \ in S $ und so weiter]
Die assoziative Eigenschaft gilt auch für jedes Element $ a, b, c \ in S, (a \ mal b) \ mal c = a \ mal (b \ mal c) $ [Zum Beispiel $ (1 \ mal 2) \ mal 3 = 1 \ mal (2 \ mal 3) = 6 $ und so weiter]
Die Identitätseigenschaft gilt auch für jedes Element $ a \ in S, (a \ mal e) = a $ [Zum Beispiel $ (2 \ mal 1) = 2, (3 \ mal 1) = 3 $ und so weiter]. Hier ist das Identitätselement 1.
Gruppe
Eine Gruppe ist ein Monoid mit einem inversen Element. Das inverse Element (bezeichnet mit I) einer Menge S ist ein Element, so dass $ (a \ omicron I) = (I \ omicron a) = a $ für jedes Element $ a \ in S $. Eine Gruppe hat also gleichzeitig vier Eigenschaften: i) Abschluss, ii) Assoziativ, iii) Identitätselement, iv) Inverses Element. Die Reihenfolge einer Gruppe G ist die Anzahl der Elemente in G und die Reihenfolge eines Elements in einer Gruppe ist die am wenigsten positive ganze Zahl n, so dass an das Identitätselement dieser Gruppe G ist.
Beispiele
Die Menge von $ N \ mal N $ nicht singulären Matrizen bildet eine Gruppe unter Matrixmultiplikationsoperation.
Das Produkt von zwei nicht singulären $ N \ mal N $ -Matrizen ist auch eine nicht singuläre $ N \ mal N $ -Matrix, die die Schließungseigenschaft enthält.
Die Matrixmultiplikation selbst ist assoziativ. Daher gilt assoziatives Eigentum.
Die Menge der nicht singulären Matrizen $ N \ times N $ enthält die Identitätsmatrix, die die Eigenschaft des Identitätselements enthält.
Da alle Matrizen nicht singulär sind, haben sie alle inverse Elemente, die auch nicht singuläre Matrizen sind. Daher gilt auch die inverse Eigenschaft.
Abelsche Gruppe
Eine abelsche Gruppe G ist eine Gruppe, für die das Elementpaar $ (a, b) \ in G $ immer das kommutative Gesetz enthält. Eine Gruppe hat also fünf Eigenschaften gleichzeitig - i) Abschluss, ii) Assoziativ, iii) Identitätselement, iv) Inverses Element, v) Kommutativ.
Beispiel
Die Menge der positiven ganzen Zahlen (einschließlich Null) mit Additionsoperation ist eine abelsche Gruppe. $ G = \ lbrace 0, 1, 2, 3, \ dots \ rbrace $
Hier gilt die Closure-Eigenschaft wie für jedes Paar $ (a, b) \ in S, (a + b) $ ist in der Menge S vorhanden. [Zum Beispiel $ 1 + 2 = 2 \ in S $ und so weiter]
Die assoziative Eigenschaft gilt auch für jedes Element $ a, b, c \ in S, (a + b) + c = a + (b + c) $ [Zum Beispiel $ (1 + 2) + 3 = 1 + (2) + 3) = 6 $ und so weiter]
Die Identitätseigenschaft gilt auch für jedes Element $ a \ in S, (a \ mal e) = a $ [Zum Beispiel $ (2 \ mal 1) = 2, (3 \ mal 1) = 3 $ und so weiter]. Hier ist das Identitätselement 1.
Die kommutative Eigenschaft gilt auch für jedes Element $ a \ in S, (a \ mal b) = (b \ mal a) $ [Zum Beispiel $ (2 \ mal 3) = (3 \ mal 2) = 3 $ und so weiter auf]
Zyklische Gruppe und Untergruppe
EIN cyclic groupist eine Gruppe, die von einem einzelnen Element generiert werden kann. Jedes Element einer zyklischen Gruppe ist eine Potenz eines bestimmten Elements, das als Generator bezeichnet wird. Eine zyklische Gruppe kann durch einen Generator 'g' erzeugt werden, so dass jedes andere Element der Gruppe als eine Leistung des Generators 'g' geschrieben werden kann.
Beispiel
Die Menge der komplexen Zahlen $ \ lbrace 1, -1, i, -i \ rbrace $ unter Multiplikationsoperation ist eine zyklische Gruppe.
Es gibt zwei Generatoren - $ i $ und $ –i $ als $ i ^ 1 = i, i ^ 2 = -1, i ^ 3 = -i, i ^ 4 = 1 $ und auch $ (- i) ^ 1 = -i, (–i) ^ 2 = -1, (–i) ^ 3 = i, (–i) ^ 4 = 1 $, was alle Elemente der Gruppe abdeckt. Daher ist es eine zyklische Gruppe.
Note - A. cyclic groupist immer eine abelsche Gruppe, aber nicht jede abelsche Gruppe ist eine zyklische Gruppe. Die hinzugefügten rationalen Zahlen sind nicht zyklisch, sondern abelsch.
EIN subgroup H ist eine Teilmenge einer Gruppe G (bezeichnet mit $ H ≤ G $), wenn es die vier Eigenschaften gleichzeitig erfüllt - Closure, Associative, Identity element, und Inverse.
Eine Untergruppe H einer Gruppe G, die nicht die gesamte Gruppe G enthält, wird als richtige Untergruppe bezeichnet (bezeichnet mit $ H <G $). Eine Untergruppe einer zyklischen Gruppe ist zyklisch und eine abelsche Untergruppe ist ebenfalls abelisch.
Beispiel
Lassen Sie eine Gruppe $ G = \ lbrace 1, i, -1, -i \ rbrace $
Dann sind einige Untergruppen $ H_1 = \ lbrace 1 \ rbrace, H_2 = \ lbrace 1, -1 \ rbrace $,
Dies ist keine Untergruppe - $ H_3 = \ lbrace 1, i \ rbrace $, da $ (i) ^ {- 1} = -i $ nicht in $ H_3 $ enthalten ist
Teilweise bestelltes Set (POSET)
Eine teilweise geordnete Menge besteht aus einer Menge mit einer binären Beziehung, die reflexiv, antisymmetrisch und transitiv ist. "Teilweise geordneter Satz" wird als POSET abgekürzt.
Beispiele
Die Menge der reellen Zahlen unter binärer Operation kleiner oder gleich $ (\ le) $ ist ein Poset.
Lassen Sie die Menge $ S = \ lbrace 1, 2, 3 \ rbrace $ und die Operation ist $ \ le $
Die Beziehungen sind $ \ lbrace (1, 1), (2, 2), (3, 3), (1, 2), (1, 3), (2, 3) \ rbrace $
Diese Beziehung R ist reflexiv als $ \ lbrace (1, 1), (2, 2), (3, 3) \ rbrace \ in R $
Diese Beziehung R ist antisymmetrisch, wie
$ \ lbrace (1, 2), (1, 3), (2, 3) \ rbrace \ in R \ und \ \ lbrace (1, 2), (1, 3), (2, 3) \ rbrace ∉ R $
Diese Beziehung R ist auch transitiv als $ \ lbrace (1,2), (2,3), (1,3) \ rbrace \ in R $.
Daher ist es ein poset.
Der Scheitelpunktsatz eines gerichteten azyklischen Graphen unter der Operation 'Erreichbarkeit' ist ein Poset.
Hasse Diagramm
Das Hasse-Diagramm eines Posets ist der gerichtete Graph, dessen Eckpunkte das Element dieses Posets sind und dessen Bögen die Paare (x, y) im Poset abdecken. Wenn im Poset $ x <y $, erscheint der Punkt x niedriger als der Punkt y im Hasse-Diagramm. Wenn $ x <y <z $ im Poset ist, wird der Pfeil nicht implizit zwischen x und z angezeigt.
Beispiel
Die Menge der Teilmengen von $ \ lbrace 1, 2, 3 \ rbrace = \ lbrace \ Emptyset, \ lbrace 1 \ rbrace, \ lbrace 2 \ rbrace, \ lbrace 3 \ rbrace, \ lbrace 1, 2 \ rbrace, \ lbrace 1 , 3 \ rbrace, \ lbrace 2, 3 \ rbrace, \ lbrace 1, 2, 3 \ rbrace \ rbrace $ wird durch das folgende Hasse-Diagramm dargestellt:
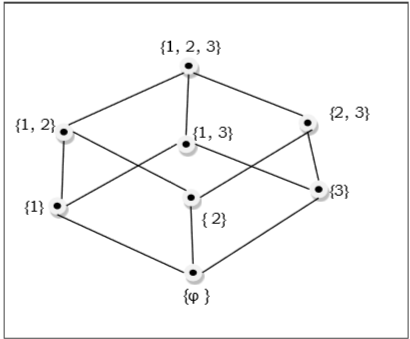
Linear geordnetes Set
Eine linear geordnete Menge oder eine insgesamt geordnete Menge ist eine Teilordnungsmenge, in der jedes Elementpaar vergleichbar ist. Die Elemente $ a, b \ in S $ gelten als vergleichbar, wenn entweder $ a \ le b $ oder $ b \ le a $ gilt. Das Trichotomiegesetz definiert diese geordnete Gesamtmenge. Eine vollständig geordnete Menge kann als ein Verteilungsgitter mit der Eigenschaft $ \ lbrace a \ lor b, a \ land b \ rbrace = \ lbrace a, b \ rbrace $ für alle Werte von a und b in Menge S definiert werden.
Beispiel
Das von \ subseteq geordnete Powerset von $ \ lbrace a, b \ rbrace $ ist eine vollständig geordnete Menge, da alle Elemente des Power-Sets $ P = \ lbrace \ Emptyset, \ lbrace a \ rbrace, \ lbrace b \ rbrace, \ lbrace a, b \ rbrace \ rbrace $ sind vergleichbar.
Beispiel für einen nicht vollständigen Auftragssatz
Eine Menge $ S = \ lbrace 1, 2, 3, 4, 5, 6 \ rbrace $ unter Operation x dividiert y ist keine insgesamt geordnete Menge.
Hier für alle $ (x, y) \ in S, x | y $ müssen halten, aber es ist nicht wahr, dass 2 | 3, da 2 3 nicht teilt oder 3 2 nicht teilt. Daher ist es keine insgesamt geordnete Menge.
Gitter
Ein Gitter ist ein Poset $ (L, \ le) $, für das jedes Paar $ \ lbrace a, b \ rbrace \ in L $ eine kleinste Obergrenze (bezeichnet mit $ a \ lor b $) und eine größte Untergrenze (bezeichnet) hat. bezeichnet mit $ a \ land b $). LUB $ (\ lbrace a, b \ rbrace) $ heißt die Verknüpfung von a und b. GLB $ (\ lbrace a, b \ rbrace) $ heißt das Treffen von a und b.
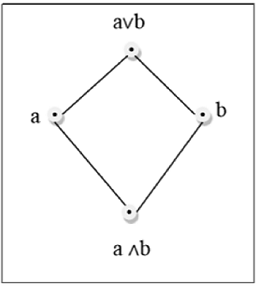
Beispiel
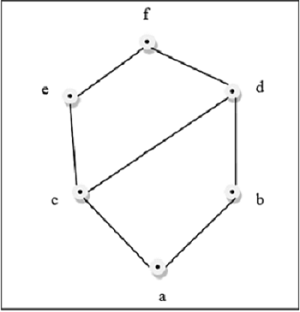
Diese obige Abbildung ist ein Gitter, da für jedes Paar $ \ lbrace a, b \ rbrace \ in L $ ein GLB und ein LUB existieren.
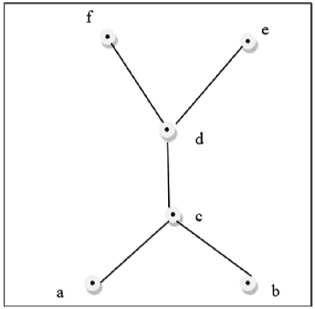
Diese obige Abbildung ist kein Gitter, da $ GLB (a, b) $ und $ LUB (e, f) $ nicht existieren.
Einige andere Gitter werden unten diskutiert -
Begrenztes Gitter
Ein Gitter L wird zu einem begrenzten Gitter, wenn es ein größtes Element 1 und ein kleinstes Element 0 hat.
Ergänztes Gitter
Ein Gitter L wird zu einem komplementierten Gitter, wenn es ein begrenztes Gitter ist und wenn jedes Element im Gitter ein Komplement hat. Ein Element x hat ein Komplement x ', wenn $ \ existiert x (x \ land x' = 0 und x \ lor x '= 1) $
Verteilungsgitter
Wenn ein Gitter die folgenden zwei Verteilungseigenschaften erfüllt, wird es als Verteilungsgitter bezeichnet.
$ a \ lor (b \ land c) = (a \ lor b) \ land (a \ lor c) $
$ a \ land (b \ lor c) = (a \ land b) \ lor (a \ land c) $
Modulares Gitter
Wenn ein Gitter die folgende Eigenschaft erfüllt, wird es als modulares Gitter bezeichnet.
$ a \ land (b \ lor (a \ land d)) = (a \ land b) \ lor (a \ land d) $
Eigenschaften von Gittern
Idempotente Eigenschaften
$ a \ lor a = a $
$ a \ land a = a $
Absorptionseigenschaften
$ a \ lor (a \ land b) = a $
$ a \ land (a \ lor b) = a $
Kommutative Eigenschaften
$ a \ lor b = b \ lor a $
$ a \ land b = b \ land a $
Assoziative Eigenschaften
$ a \ lor (b \ lor c) = (a \ lor b) \ lor c $
$ a \ land (b \ land c) = (a \ land b) \ land c $
Dual eines Gitters
Das Dual eines Gitters wird durch Vertauschen der Operationen '$ \ lor $' und '$ \ land $' erhalten.
Beispiel
Das Dual von $ \ lbrack a \ lor (b \ land c) \ rbrack \ ist \ \ lbrack a \ land (b \ lor c) \ rbrack $