Diskrete Mathematik - Mengen
Deutscher Mathematiker G. Cantorführte das Konzept der Mengen ein. Er hatte eine Menge als eine Sammlung bestimmter und unterscheidbarer Objekte definiert, die anhand bestimmter Regeln oder Beschreibungen ausgewählt wurden.
SetDie Theorie bildet die Grundlage für mehrere andere Studienbereiche wie Zähltheorie, Beziehungen, Graphentheorie und endliche Zustandsmaschinen. In diesem Kapitel werden wir die verschiedenen Aspekte von behandelnSet Theory.
Set - Definition
Ein Set ist eine ungeordnete Sammlung verschiedener Elemente. Ein Set kann explizit geschrieben werden, indem seine Elemente mit der Set-Klammer aufgelistet werden. Wenn die Reihenfolge der Elemente geändert oder ein Element einer Menge wiederholt wird, werden keine Änderungen an der Menge vorgenommen.
Ein Beispiel für Sets
- Eine Menge aller positiven ganzen Zahlen
- Eine Reihe aller Planeten im Sonnensystem
- Eine Reihe aller Staaten in Indien
- Ein Satz aller Kleinbuchstaben des Alphabets
Darstellung eines Sets
Sets können auf zwei Arten dargestellt werden:
- Dienstplan oder Tabellenform
- Legen Sie die Builder-Notation fest
Dienstplan oder Tabellenform
Die Menge wird dargestellt, indem alle Elemente aufgelistet werden, aus denen sie besteht. Die Elemente sind in geschweiften Klammern eingeschlossen und durch Kommas getrennt.
Example 1 - Satz von Vokalen im englischen Alphabet, $ A = \ lbrace a, e, i, o, u \ rbrace $
Example 2 - Satz ungerader Zahlen unter 10, $ B = \ lbrace 1,3,5,7,9 \ rbrace $
Legen Sie die Builder-Notation fest
Die Menge wird definiert, indem eine Eigenschaft angegeben wird, die Elemente der Menge gemeinsam haben. Die Menge wird beschrieben als $ A = \ lbrace x: p (x) \ rbrace $
Example 1 - Die Menge $ \ lbrace a, e, i, o, u \ rbrace $ ist geschrieben als -
$ A = \ lbrace x: \ text {x ist ein Vokal im englischen Alphabet} \ rbrace $
Example 2 - Die Menge $ \ lbrace 1,3,5,7,9 \ rbrace $ ist geschrieben als -
$ B = \ lbrace x: 1 \ le x \ lt 10 \ und \ (x \% 2) \ ne 0 \ rbrace $
Wenn ein Element x ein Mitglied einer Menge S ist, wird es in S $ mit $ x \ bezeichnet, und wenn ein Element y kein Mitglied der Menge S ist, wird es mit $ y \ notin S $ bezeichnet.
Example- Wenn $ S = \ lbrace1, 1.2, 1.7, 2 \ rbrace, 1 \ in S $, aber $ 1.5 \ notin S $
Einige wichtige Sätze
N - die Menge aller natürlichen Zahlen = $ \ lbrace1, 2, 3, 4, ..... \ rbrace $
Z - die Menge aller ganzen Zahlen = $ \ lbrace ....., -3, -2, -1, 0, 1, 2, 3, ..... \ rbrace $
Z+ - die Menge aller positiven ganzen Zahlen
Q - die Menge aller rationalen Zahlen
R - die Menge aller reellen Zahlen
W - die Menge aller ganzen Zahlen
Kardinalität einer Menge
Die Kardinalität einer Menge S, bezeichnet mit $ | S | $, ist die Anzahl der Elemente der Menge. Die Nummer wird auch als Kardinalzahl bezeichnet. Wenn eine Menge unendlich viele Elemente hat, ist ihre Kardinalität $ \ infty $.
Example- $ | \ lbrace 1, 4, 3, 5 \ rbrace | = 4, | \ lbrace 1, 2, 3, 4, 5, \ dots \ rbrace | = \ infty $
Wenn es zwei Sätze X und Y gibt,
$ | X | = | Y | $ bezeichnet zwei Mengen X und Y mit derselben Kardinalität. Es tritt auf, wenn die Anzahl der Elemente in X genau der Anzahl der Elemente in Y entspricht. In diesem Fall existiert eine bijektive Funktion 'f' von X nach Y.
$ | X | \ le | Y | $ bedeutet, dass die Kardinalität von Satz X kleiner oder gleich der Kardinalität von Satz Y ist. Es tritt auf, wenn die Anzahl der Elemente in X kleiner oder gleich der von Y ist. Hier existiert eine Injektionsfunktion 'f' von X nach Y.
$ | X | \ lt | Y | $ bedeutet, dass die Kardinalität von Satz X geringer ist als die Kardinalität von Satz Y. Es tritt auf, wenn die Anzahl der Elemente in X kleiner als die von Y ist. Hier ist die Funktion 'f' von X nach Y eine injektive Funktion, aber keine bijektive.
$ If \ | X | \ le | Y | $ und $ | X | \ ge | Y | $ dann $ | X | = | Y | $. Die Mengen X und Y werden üblicherweise als äquivalente Mengen bezeichnet.
Arten von Sets
Sets können in viele Typen eingeteilt werden. Einige davon sind endlich, unendlich, Teilmenge, universell, richtig, Singleton-Menge usw.
Endliche Menge
Eine Menge, die eine bestimmte Anzahl von Elementen enthält, wird als endliche Menge bezeichnet.
Example- $ S = \ lbrace x \: | \: x \ in N $ und $ 70 \ gt x \ gt 50 \ rbrace $
Unendliches Set
Eine Menge, die unendlich viele Elemente enthält, wird als unendliche Menge bezeichnet.
Example- $ S = \ lbrace x \: | \: x \ in N $ und $ x \ gt 10 \ rbrace $
Teilmenge
Eine Menge X ist eine Teilmenge der Menge Y (geschrieben als $ X \ subseteq Y $), wenn jedes Element von X ein Element der Menge Y ist.
Example 1- Sei $ X = \ lbrace 1, 2, 3, 4, 5, 6 \ rbrace $ und $ Y = \ lbrace 1, 2 \ rbrace $. Hier ist die Menge Y eine Teilmenge der Menge X, da sich alle Elemente der Menge Y in der Menge X befinden. Daher können wir $ Y \ subseteq X $ schreiben.
Example 2- Sei $ X = \ lbrace 1, 2, 3 \ rbrace $ und $ Y = \ lbrace 1, 2, 3 \ rbrace $. Hier ist Menge Y eine Teilmenge (keine richtige Teilmenge) von Menge X, da sich alle Elemente von Menge Y in Menge X befinden. Daher können wir $ Y \ subseteq X $ schreiben.
Echte Teilmenge
Der Begriff "richtige Teilmenge" kann als "Teilmenge von, aber nicht gleich" definiert werden. Eine Menge X ist eine richtige Teilmenge der Menge Y (geschrieben als $ X \ Teilmenge Y $), wenn jedes Element von X ein Element der Menge Y und $ | X | ist \ lt | Y | $.
Example- Sei $ X = \ lbrace 1, 2, 3, 4, 5, 6 \ rbrace $ und $ Y = \ lbrace 1, 2 \ rbrace $. Hier setzen Sie $ Y \ Teilmenge X $, da alle Elemente in $ Y $ auch in $ X $ enthalten sind und $ X $ mindestens ein Element hat, das mehr als die Menge $ Y $ ist.
Universelles Set
Es ist eine Sammlung aller Elemente in einem bestimmten Kontext oder einer bestimmten Anwendung. Alle Mengen in diesem Kontext oder in dieser Anwendung sind im Wesentlichen Teilmengen dieser universellen Menge. Universelle Mengen werden als $ U $ dargestellt.
Example- Wir können $ U $ als die Menge aller Tiere auf der Erde definieren. In diesem Fall ist die Menge aller Säugetiere eine Teilmenge von $ U $, die Menge aller Fische eine Teilmenge von $ U $, die Menge aller Insekten eine Teilmenge von $ U $ und so weiter.
Leerer Satz oder Nullsatz
Ein leerer Satz enthält keine Elemente. Es wird mit $ \ Emptyset $ bezeichnet. Da die Anzahl der Elemente in einer leeren Menge endlich ist, ist die leere Menge eine endliche Menge. Die Kardinalität der leeren Menge oder der Nullmenge ist Null.
Example- $ S = \ lbrace x \: | \: x \ in N $ und $ 7 \ lt x \ lt 8 \ rbrace = \ Emptyset $
Singleton Set oder Unit Set
Singleton-Set oder Unit-Set enthält nur ein Element. Eine Singleton-Menge wird mit $ \ lbrace s \ rbrace $ bezeichnet.
Example- $ S = \ lbrace x \: | \: x \ in N, \ 7 \ lt x \ lt 9 \ rbrace $ = $ \ lbrace 8 \ rbrace $
Gleicher Satz
Wenn zwei Mengen dieselben Elemente enthalten, werden sie als gleich bezeichnet.
Example - Wenn $ A = \ lbrace 1, 2, 6 \ rbrace $ und $ B = \ lbrace 6, 1, 2 \ rbrace $, sind sie gleich, da jedes Element von Satz A ein Element von Satz B und jedes Element von Satz ist B ist ein Element der Menge A.
Äquivalenter Satz
Wenn die Kardinalitäten zweier Mengen gleich sind, werden sie als äquivalente Mengen bezeichnet.
Example- Wenn $ A = \ lbrace 1, 2, 6 \ rbrace $ und $ B = \ lbrace 16, 17, 22 \ rbrace $, sind sie äquivalent, da die Kardinalität von A gleich der Kardinalität von B ist, dh $ | A | = | B | = 3 $
Überlappender Satz
Zwei Mengen mit mindestens einem gemeinsamen Element werden als überlappende Mengen bezeichnet.
Bei überlappenden Mengen -
$ n (A \ Tasse B) = n (A) + n (B) - n (A \ Kappe B) $
$ n (A \ Tasse B) = n (A - B) + n (B - A) + n (A \ Kappe B) $
$ n (A) = n (A - B) + n (A \ cap B) $
$ n (B) = n (B - A) + n (A \ cap B) $
Example- Sei $ A = \ lbrace 1, 2, 6 \ rbrace $ und $ B = \ lbrace 6, 12, 42 \ rbrace $. Es gibt ein gemeinsames Element '6', daher sind diese Mengen überlappende Mengen.
Disjunktes Set
Zwei Mengen A und B werden disjunkte Mengen genannt, wenn sie nicht einmal ein Element gemeinsam haben. Daher haben disjunkte Mengen die folgenden Eigenschaften:
$ n (A \ cap B) = \ Emptyset $
$ n (A \ Tasse B) = n (A) + n (B) $
Example - Es sei $ A = \ lbrace 1, 2, 6 \ rbrace $ und $ B = \ lbrace 7, 9, 14 \ rbrace $, es gibt kein einziges gemeinsames Element, daher sind diese Mengen überlappende Mengen.
Venn-Diagramme
Das 1880 von John Venn erfundene Venn-Diagramm ist ein schematisches Diagramm, das alle möglichen logischen Beziehungen zwischen verschiedenen mathematischen Mengen zeigt.
Examples
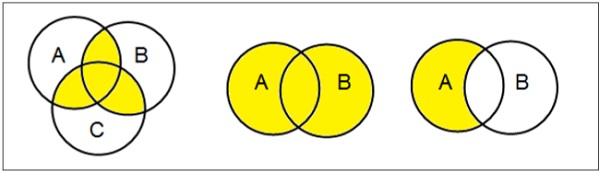
Operationen einstellen
Zu den Set-Operationen gehören Set Union, Set Intersection, Set Difference, Complement of Set und Cartesian Product.
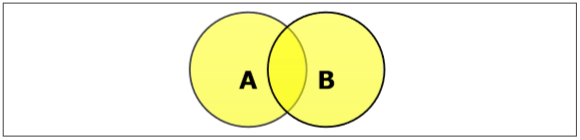
Set Union
Die Vereinigung der Mengen A und B (bezeichnet mit $ A \ cup B $) ist die Menge der Elemente, die sich in A, in B oder sowohl in A als auch in B befinden. Daher ist $ A \ cup B = \ lbrace x \: | \: x \ in A \ OR \ x \ in B \ rbrace $.
Example- Wenn $ A = \ lbrace 10, 11, 12, 13 \ rbrace $ und B = $ \ lbrace 13, 14, 15 \ rbrace $, dann $ A \ cup B = \ lbrace 10, 11, 12, 13, 14 , 15 \ rbrace $. (Das gemeinsame Element kommt nur einmal vor)
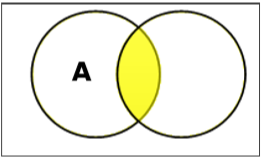
Schnittpunkt einstellen
Der Schnittpunkt der Mengen A und B (bezeichnet mit $ A \ cap B $) ist die Menge der Elemente, die sich sowohl in A als auch in B befinden. Daher ist $ A \ cap B = \ lbrace x \: | \: x \ in A. \ AND \ x \ in B \ rbrace $.
Example - Wenn $ A = \ lbrace 11, 12, 13 \ rbrace $ und $ B = \ lbrace 13, 14, 15 \ rbrace $, dann $ A \ cap B = \ lbrace 13 \ rbrace $.
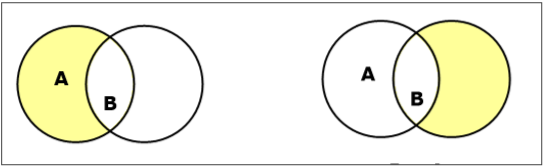
Differenz / relative Ergänzung einstellen
Die Mengendifferenz der Mengen A und B (bezeichnet mit $ A - B $) ist die Menge der Elemente, die sich nur in A, aber nicht in B befinden. Daher ist $ A - B = \ lbrace x \: | \: x \ in A \ AND \ x \ notin B \ rbrace $.
Example- Wenn $ A = \ lbrace 10, 11, 12, 13 \ rbrace $ und $ B = \ lbrace 13, 14, 15 \ rbrace $, dann ist $ (A - B) = \ lbrace 10, 11, 12 \ rbrace $ und $ (B - A) = \ lbrace 14, 15 \ rbrace $. Hier sehen wir $ (A - B) \ ne (B - A) $
Ergänzung eines Sets
Das Komplement einer Menge A (bezeichnet mit $ A '$) ist die Menge von Elementen, die nicht in Menge A enthalten sind. Daher ist $ A' = \ lbrace x | x \ notin A \ rbrace $.
Insbesondere ist $ A '= (U - A) $, wobei $ U $ eine universelle Menge ist, die alle Objekte enthält.
Example- Wenn $ A = \ lbrace x \: | \: x \ \: {gehört \: zu \: set \: of \: odd \: integers} \ rbrace $ then $ A '= \ lbrace y \: | \: y \ \: {gehört \: nicht \: zu \: zu \: set \: of \: odd \: integers} \ rbrace $

Kartesisches Produkt / Kreuzprodukt
Das kartesische Produkt von n Anzahlen von $ A_1, A_2, \ Punkten A_n $, bezeichnet als $ A_1 \ mal A_2 \ Punkte \ mal A_n $, kann als alle möglichen geordneten Paare $ (x_1, x_2, \ Punkte x_n) $ definiert werden, wobei $ x_1 \ in A_1, x_2 \ in A_2, \ Punkte x_n \ in A_n $
Example - Wenn wir zwei Sätze nehmen $ A = \ lbrace a, b \ rbrace $ und $ B = \ lbrace 1, 2 \ rbrace $,
Das kartesische Produkt von A und B wird geschrieben als - $ A \ mal B = \ lbrace (a, 1), (a, 2), (b, 1), (b, 2) \ rbrace $
Das kartesische Produkt von B und A wird geschrieben als - $ B \ mal A = \ lbrace (1, a), (1, b), (2, a), (2, b) \ rbrace $
Power Set
Potenzmenge einer Menge S ist die Menge aller Teilmengen von S einschließlich der leeren Menge. Die Kardinalität eines Potenzsatzes eines Satzes S der Kardinalität n beträgt $ 2 ^ n $. Die eingestellte Leistung wird als $ P (S) $ bezeichnet.
Example −
Für eine Menge $ S = \ lbrace a, b, c, d \ rbrace $ berechnen wir die Teilmengen -
Teilmengen mit 0 Elementen - $ \ lbrace \ Emptyset \ rbrace $ (die leere Menge)
Teilmengen mit 1 Element - $ \ lbrace a \ rbrace, \ lbrace b \ rbrace, \ lbrace c \ rbrace, \ lbrace d \ rbrace $
Teilmengen mit 2 Elementen - $ \ lbrace a, b \ rbrace, \ lbrace a, c \ rbrace, \ lbrace a, d \ rbrace, \ lbrace b, c \ rbrace, \ lbrace b, d \ rbrace, \ lbrace c, d \ rbrace $
Teilmengen mit 3 Elementen - $ \ lbrace a, b, c \ rbrace, \ lbrace a, b, d \ rbrace, \ lbrace a, c, d \ rbrace, \ lbrace b, c, d \ rbrace $
Teilmengen mit 4 Elementen - $ \ lbrace a, b, c, d \ rbrace $
Daher ist $ P (S) = $
US-Dollar rbrace, \ lbrace a, d \ rbrace, \ lbrace b, c \ rbrace, \ lbrace b, d \ rbrace, \ lbrace c, d \ rbrace, \ lbrace a, b, c \ rbrace, \ lbrace a, b, d \ rbrace, \ lbrace a, c, d \ rbrace, \ lbrace b, c, d \ rbrace, \ lbrace a, b, c, d \ rbrace \ quad \ rbrace $
$ | P (S) | = 2 ^ 4 = 16 $
Note - Der Energiesatz eines leeren Satzes ist ebenfalls ein leerer Satz.
$ | P (\ lbrace \ Emptyset \ rbrace) | = 2 ^ 0 = 1 $
Partitionierung eines Sets
Die Partition einer Menge, z. B. S , ist eine Sammlung von n disjunkten Teilmengen, z. B. $ P_1, P_2, \ dots P_n $, die die folgenden drei Bedingungen erfüllt:
$ P_i $ enthält nicht die leere Menge.
$ \ lbrack P_i \ ne \ lbrace \ emptyset \ rbrace \ für \ all \ 0 \ lt i \ le n \ rbrack $
Die Vereinigung der Teilmengen muss der gesamten ursprünglichen Menge entsprechen.
$ \ lbrack P_1 \ cup P_2 \ cup \ dots \ cup P_n = S \ rbrack $
Der Schnittpunkt zweier unterschiedlicher Mengen ist leer.
$ \ lbrack P_a \ cap P_b = \ lbrace \ Emptyset \ rbrace, \ für \ a \ ne b \ wobei \ n \ ge a, \: b \ ge 0 \ rbrack $
Example
Sei $ S = \ lbrace a, b, c, d, e, f, g, h \ rbrace $
Eine wahrscheinliche Partitionierung ist $ \ lbrace a \ rbrace, \ lbrace b, c, d \ rbrace, \ lbrace e, f, g, h \ rbrace $
Eine andere wahrscheinliche Partitionierung ist $ \ lbrace a, b \ rbrace, \ lbrace c, d \ rbrace, \ lbrace e, f, g, h \ rbrace $
Glockennummern
Glockennummern geben die Anzahl der Möglichkeiten an, eine Menge zu partitionieren. Sie werden mit $ B_n $ bezeichnet, wobei n die Kardinalität der Menge ist.
Example - -
Sei $ S = \ lbrace 1, 2, 3 \ rbrace $, $ n = | S | = 3 $
Die alternativen Partitionen sind -
1. $ \ Emptyset, \ lbrace 1, 2, 3 \ rbrace $
2. $ \ lbrace 1 \ rbrace, \ lbrace 2, 3 \ rbrace $
3. $ \ lbrace 1, 2 \ rbrace, \ lbrace 3 \ rbrace $
4. $ \ lbrace 1, 3 \ rbrace, \ lbrace 2 \ rbrace $
5. $ \ lbrace 1 \ rbrace, \ lbrace 2 \ rbrace, \ lbrace 3 \ rbrace $
Daher ist $ B_3 = 5 $