Vereinfachung boolescher Funktionen

Vereinfachung mit algebraischen Funktionen

Bei diesem Ansatz wird ein Boolescher Ausdruck durch Anwenden von Booleschen Identitäten zu einem äquivalenten Ausdruck minimiert.

Problem 1

Minimieren Sie den folgenden Booleschen Ausdruck mit Booleschen Identitäten -

$$ F (A, B, C) = A'B + BC '+ BC + AB'C' $$

Lösung

Gegeben ist $ F (A, B, C) = A'B + BC '+ BC + AB'C' $

Oder $ F (A, B, C) = A'B + (BC '+ BC') + BC + AB'C '$

[Nach idempotentem Gesetz ist BC '= BC' + BC ']

Oder $ F (A, B, C) = A'B + (BC '+ BC) + (BC' + AB'C ') $

Oder $ F (A, B, C) = A'B + B (C '+ C) + C' (B + AB ') $

[Durch Verteilungsgesetze]

Oder $ F (A, B, C) = A'B + B.1 + C '(B + A) $

[(C '+ C) = 1 und Absorptionsgesetz (B + AB') = (B + A)]

Oder $ F (A, B, C) = A'B + B + C '(B + A) $

[B.1 = B]

Oder $ F (A, B, C) = B (A '+ 1) + C' (B + A) $

Oder $ F (A, B, C) = B.1 + C '(B + A) $

[(A '+ 1) = 1]

Oder $ F (A, B, C) = B + C '(B + A) $

[As, B.1 = B]

Oder $ F (A, B, C) = B + BC '+ AC' $

Oder $ F (A, B, C) = B (1 + C ') + AC' $

Oder $ F (A, B, C) = B.1 + AC '$

[As, (1 + C ') = 1]

Oder $ F (A, B, C) = B + AC '$

[As, B.1 = B]

Also ist $ F (A, B, C) = B + AC '$ die minimierte Form.

Problem 2

Minimieren Sie den folgenden Booleschen Ausdruck mit Booleschen Identitäten -

$$ F (A, B, C) = (A + B) (A + C) $$

Lösung

Gegeben ist $ F (A, B, C) = (A + B) (A + C) $

Oder $ F (A, B, C) = AA + AC + BA + BC $ [Verteilungsregel anwenden]

Oder $ F (A, B, C) = A + AC + BA + BC $ [Anwendung des Idempotenten Gesetzes]

Oder $ F (A, B, C) = A (1 + C) + BA + BC $ [Anwenden des Verteilungsgesetzes]

Oder $ F (A, B, C) = A + BA + BC $ [Anwenden des Dominanzgesetzes]

Oder $ F (A, B, C) = (A + 1) .A + BC $ [Anwenden des Verteilungsgesetzes]

Oder $ F (A, B, C) = 1.A + BC $ [Anwenden des Dominanzgesetzes]

Oder $ F (A, B, C) = A + BC $ [Anwenden des Dominanzgesetzes]

Also ist $ F (A, B, C) = A + BC $ die minimierte Form.

Karnaugh Karten

Die Karnaugh-Karte (K-Karte), die 1953 von Maurice Karnaughin eingeführt wurde, ist eine gitterartige Darstellung einer Wahrheitstabelle, mit der boolesche Algebra-Ausdrücke vereinfacht werden. Eine Karnaugh-Karte enthält null und einen Eintrag an verschiedenen Positionen. Es bietet die Gruppierung von Booleschen Ausdrücken mit gemeinsamen Faktoren und eliminiert unerwünschte Variablen aus dem Ausdruck. In einer K-Karte ist das Überschreiten einer vertikalen oder horizontalen Zellgrenze immer eine Änderung nur einer Variablen.

Beispiel 1

Eine beliebige Wahrheitstabelle ist unten aufgeführt -

EIN	B.	Eine Operation B.
0	0	w
0	1	x
1	0	y
1	1	z

Jetzt machen wir eine k-Map für die obige Wahrheitstabelle -

Beispiel 2

Jetzt machen wir eine K-Map für den Ausdruck - AB + A'B '

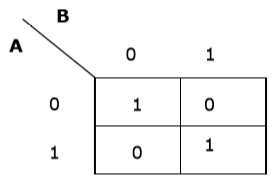
Vereinfachung mit K-Map

K-map verwendet einige Regeln zur Vereinfachung von Booleschen Ausdrücken, indem benachbarte Zellen zu einem einzigen Term kombiniert werden. Die Regeln werden unten beschrieben -

Rule 1 - Eine Zelle mit einer Null kann nicht gruppiert werden.

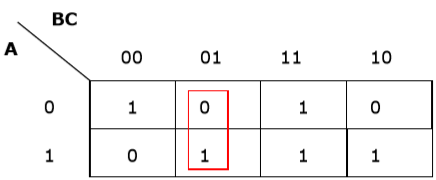
Falsche Gruppierung

Rule 2 - Gruppen müssen 2n Zellen enthalten (n ab 1).

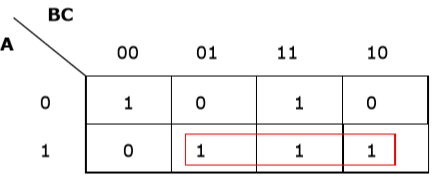
Falsche Gruppierung

Rule 3 - Die Gruppierung muss horizontal oder vertikal sein, darf jedoch nicht diagonal sein.

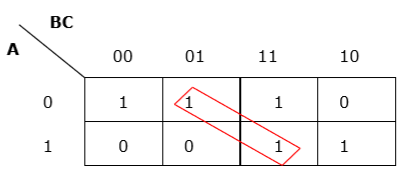
Falsche diagonale Gruppierung

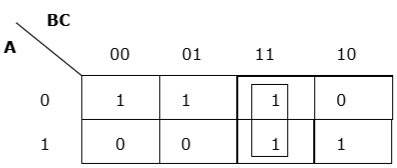
Richtige vertikale Gruppierung

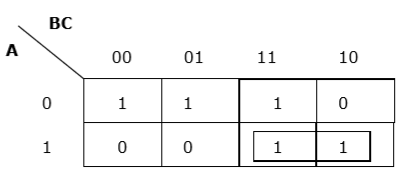
Richtige horizontale Gruppierung

Rule 4 - Gruppen müssen so weit wie möglich abgedeckt werden.

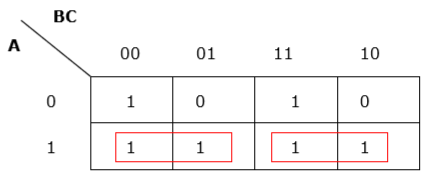
Unzureichende Gruppierung

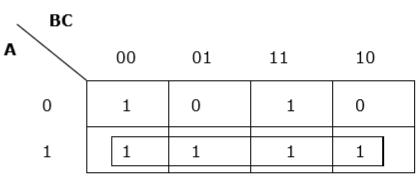
Richtige Gruppierung

Rule 5 - Wenn 1 einer Zelle nicht mit einer anderen Zelle gruppiert werden kann, fungiert sie selbst als Gruppe.

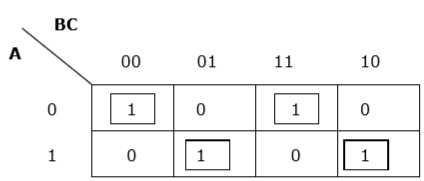
Richtige Gruppierung

Rule 6 - Gruppen können sich überschneiden, es sollten jedoch so wenige Gruppen wie möglich vorhanden sein.

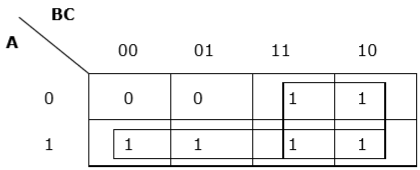
Richtige Gruppierung

Rule 7 - Die Zelle / Zellen ganz links können mit der Zelle / den Zellen ganz rechts und die Zelle / Zelle ganz oben mit der untersten Zelle / den untersten Zellen gruppiert werden.

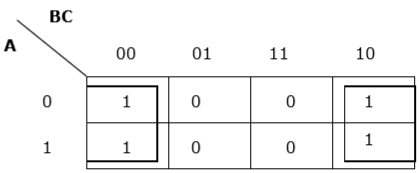
Richtige Gruppierung

Problem

Minimieren Sie den folgenden booleschen Ausdruck mit K-map -

$$ F (A, B, C) = A'BC + A'BC '+ AB'C' + AB'C $$

Lösung

Jeder Begriff wird in k-map eingefügt und wir erhalten Folgendes:

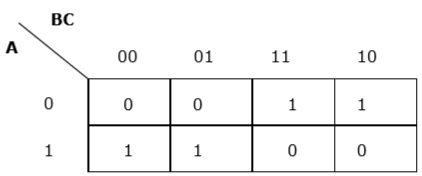
K-Karte für F (A, B, C)

Jetzt werden wir die Zellen von 1 nach den oben angegebenen Regeln gruppieren -

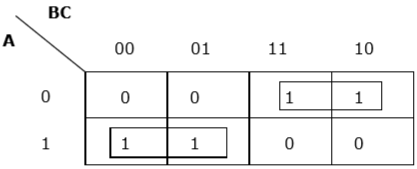
K-Karte für F (A, B, C)

Wir haben zwei Gruppen, die als $ A'B $ und $ AB '$ bezeichnet werden. Daher ist $ F (A, B, C) = A'B + AB '= A \ oplus B $. Es ist die minimierte Form.