Diskrete Mathematik - Bäume überspannen
Ein Spanning Tree eines verbundenen ungerichteten Graphen $ G $ ist ein Baum, der minimal alle Eckpunkte von $ G $ enthält. Ein Graph kann viele überspannende Bäume haben.
Beispiel
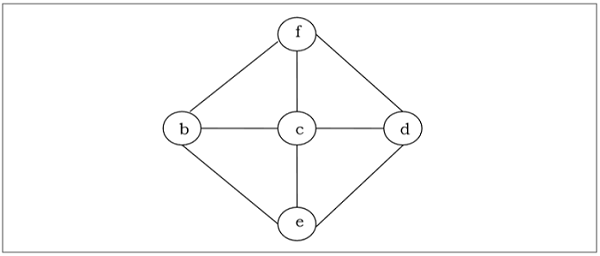
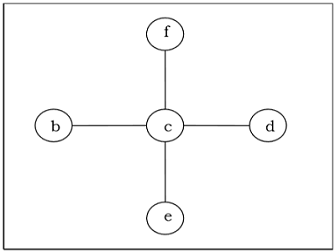
Minimum Spanning Tree
Ein Spanning Tree mit einem zugewiesenen Gewicht, das kleiner oder gleich dem Gewicht jedes möglichen Spanning Tree eines gewichteten, verbundenen und ungerichteten Graphen $ G $ ist, wird als Minimum Spanning Tree (MST) bezeichnet. Das Gewicht eines Spannbaums ist die Summe aller Gewichte, die jeder Kante des Spannbaums zugewiesen sind.
Beispiel
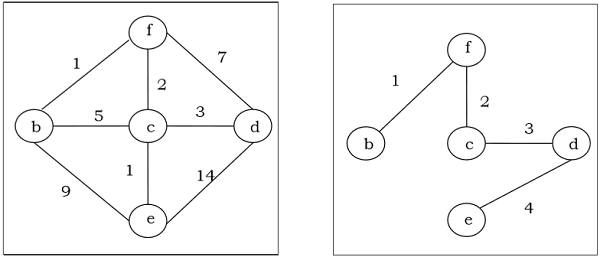
Kruskals Algorithmus
Der Kruskal-Algorithmus ist ein gieriger Algorithmus, der einen minimalen Spannbaum für einen verbundenen gewichteten Graphen findet. Es wird ein Baum dieses Diagramms gefunden, der jeden Scheitelpunkt enthält, und das Gesamtgewicht aller Kanten im Baum ist kleiner oder gleich jedem möglichen Spannbaum.
Algorithmus
Step 1 - Ordnen Sie alle Kanten des angegebenen Graphen $ G (V, E) $ in aufsteigender Reihenfolge nach ihrem Kantengewicht an.
Step 2 - Wählen Sie die kleinste gewichtete Kante aus dem Diagramm aus und prüfen Sie, ob sie mit dem bisher gebildeten Spannbaum einen Zyklus bildet.
Step 3 - Wenn es keinen Zyklus gibt, fügen Sie diese Kante in den Spanning Tree ein, andernfalls verwerfen Sie sie.
Step 4 - Wiederholen Sie Schritt 2 und Schritt 3, bis $ (V-1) $ Anzahl der Kanten im Spanning Tree verbleibt.
Problem
Angenommen, wir möchten den minimalen Spannbaum für den folgenden Graphen G unter Verwendung des Kruskal-Algorithmus finden.
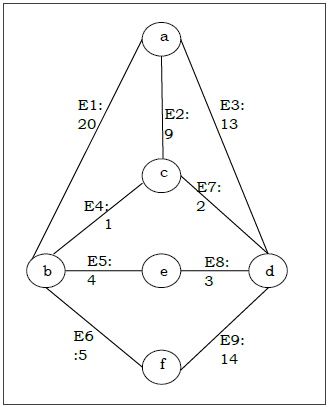
Solution
Aus der obigen Grafik konstruieren wir die folgende Tabelle:
| Rand Nr. | Scheitelpunktpaar | Kantengewicht |
|---|---|---|
| E1 | (a, b) | 20 |
| E2 | (a, c) | 9 |
| E3 | (Anzeige) | 13 |
| E4 | (b, c) | 1 |
| E5 | (Sein) | 4 |
| E6 | (b, f) | 5 |
| E7 | (c, d) | 2 |
| E8 | (d, e) | 3 |
| E9 | (d, f) | 14 |
Jetzt werden wir die Tabelle in aufsteigender Reihenfolge in Bezug auf das Kantengewicht neu anordnen -
| Rand Nr. | Scheitelpunktpaar | Kantengewicht |
|---|---|---|
| E4 | (b, c) | 1 |
| E7 | (c, d) | 2 |
| E8 | (d, e) | 3 |
| E5 | (Sein) | 4 |
| E6 | (b, f) | 5 |
| E2 | (a, c) | 9 |
| E3 | (Anzeige) | 13 |
| E9 | (d, f) | 14 |
| E1 | (a, b) | 20 |
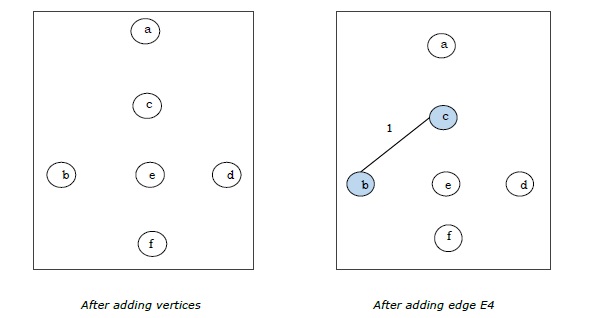
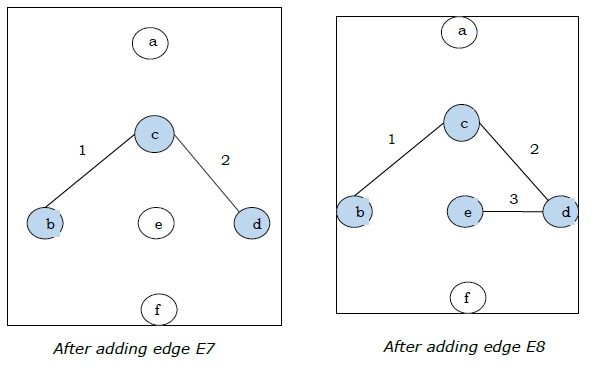
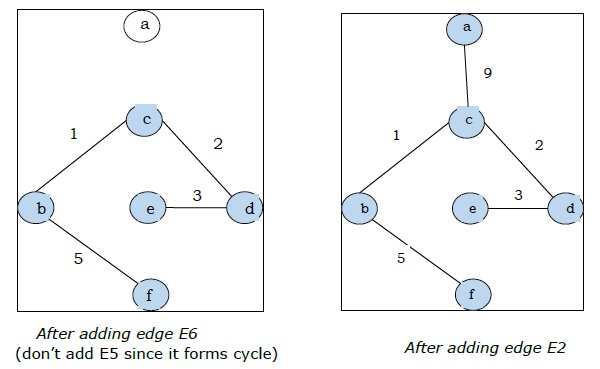
Da wir in der letzten Abbildung alle 5 Kanten erhalten haben, stoppen wir den Algorithmus. Dies ist der minimale Spannbaum und sein Gesamtgewicht beträgt $ (1 + 2 + 3 + 5 + 9) = 20 $.
Prims Algorithmus
Prims Algorithmus, der 1930 von den Mathematikern Vojtech Jarnik und Robert C. Prim entdeckt wurde, ist ein gieriger Algorithmus, der einen minimalen Spannbaum für einen verbundenen gewichteten Graphen findet. Es wird ein Baum dieses Diagramms gefunden, der jeden Scheitelpunkt enthält, und das Gesamtgewicht aller Kanten im Baum ist kleiner oder gleich jedem möglichen Spannbaum. Prims Algorithmus ist in dichten Graphen schneller.
Algorithmus
Initialisieren Sie den minimalen Spannbaum mit einem einzelnen Scheitelpunkt, der zufällig aus dem Diagramm ausgewählt wird.
Wiederholen Sie die Schritte 3 und 4, bis alle Scheitelpunkte im Baum enthalten sind.
Wählen Sie eine Kante aus, die den Baum mit einem Scheitelpunkt verbindet, der sich noch nicht im Baum befindet, sodass das Gewicht der Kante minimal ist und die Einbeziehung der Kante keinen Zyklus bildet.
Fügen Sie die ausgewählte Kante und den Scheitelpunkt hinzu, den sie mit dem Baum verbindet.
Problem
Angenommen, wir möchten den minimalen Spannbaum für den folgenden Graphen G unter Verwendung des Prim-Algorithmus finden.
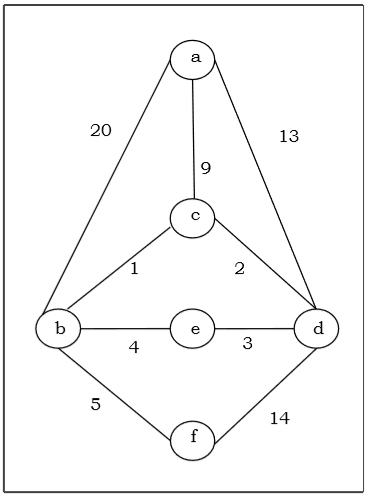
Solution
Hier beginnen wir mit dem Scheitelpunkt 'a' und fahren fort.
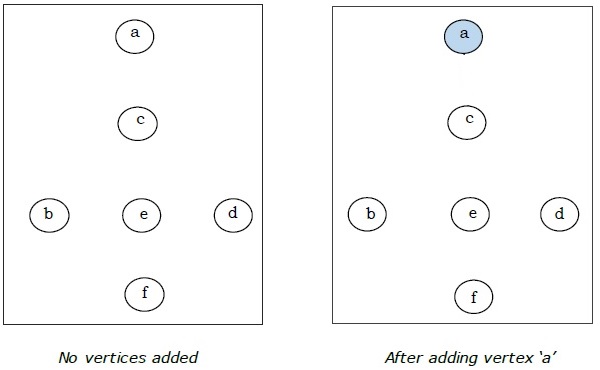
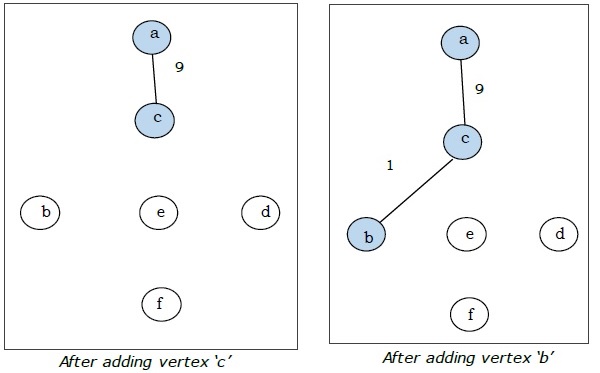
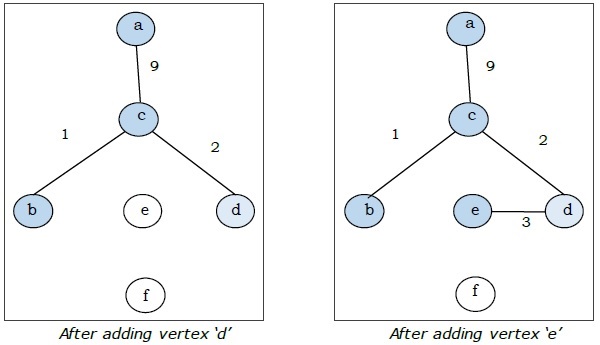
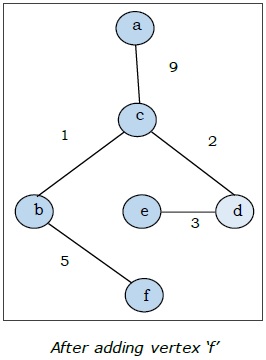
Dies ist der minimale Spannbaum und sein Gesamtgewicht beträgt $ (1 + 2 + 3 + 5 + 9) = 20 $.