Einführung in Bäume

Treeist eine diskrete Struktur, die hierarchische Beziehungen zwischen einzelnen Elementen oder Knoten darstellt. Ein Baum, in dem ein Elternteil nicht mehr als zwei Kinder hat, wird als Binärbaum bezeichnet.

Baum und seine Eigenschaften

Definition- Ein Baum ist ein verbundener azyklischer ungerichteter Graph. Es gibt einen eindeutigen Pfad zwischen jedem Scheitelpunktpaar in $ G $. Ein Baum mit N Eckpunkten enthält $ (N-1) $ Kanten. Der Scheitelpunkt von 0 Grad wird Wurzel des Baumes genannt. Der Scheitelpunkt von 1 Grad wird als Blattknoten des Baums bezeichnet, und der Grad eines internen Knotens beträgt mindestens 2.

Example - Das Folgende ist ein Beispiel für einen Baum -

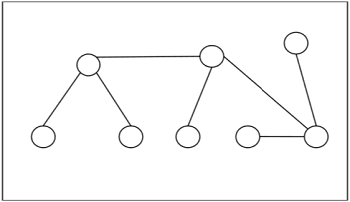
Zentren und Bi-Zentren eines Baumes

Das Zentrum eines Baumes ist ein Scheitelpunkt mit minimaler Exzentrizität. Die Exzentrizität eines Scheitelpunkts $ X $ in einem Baum $ G $ ist der maximale Abstand zwischen dem Scheitelpunkt $ X $ und einem anderen Scheitelpunkt des Baums. Die maximale Exzentrizität ist der Baumdurchmesser. Wenn ein Baum nur ein Zentrum hat, wird er als Zentralbaum bezeichnet, und wenn ein Baum nur mehr als ein Zentrum hat, wird er als Bi-Zentralbaum bezeichnet. Jeder Baum ist entweder zentral oder bizentral.

Algorithmus zum Finden von Zentren und Bi-Zentren eines Baumes

Step 1 - Entfernen Sie alle Eckpunkte des Grades 1 vom angegebenen Baum und entfernen Sie auch deren einfallende Kanten.

Step 2- Wiederholen Sie Schritt 1, bis entweder ein einzelner Scheitelpunkt oder zwei Scheitelpunkte, die durch eine Kante verbunden sind, übrig bleiben. Wenn ein einzelner Scheitelpunkt übrig bleibt, ist dies die Mitte des Baums. Wenn zwei Scheitelpunkte, die durch eine Kante verbunden sind, übrig bleiben, ist dies die Mitte des Baums.

Problem 1

Finden Sie das Zentrum / Bi-Zentrum des folgenden Baums heraus -

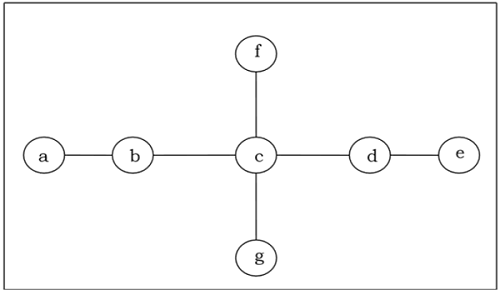
Solution

Zuerst entfernen wir alle Eckpunkte des Grades 1 und entfernen auch ihre einfallenden Kanten und erhalten den folgenden Baum -

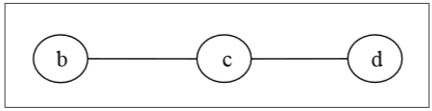
Wieder werden wir alle Eckpunkte des Grades 1 entfernen und auch ihre einfallenden Kanten entfernen und den folgenden Baum erhalten -

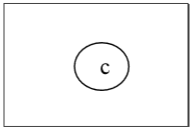
Schließlich haben wir einen einzelnen Scheitelpunkt 'c' und stoppen den Algorithmus. Da es einen einzelnen Scheitelpunkt gibt, hat dieser Baum ein zentrales 'c' und der Baum ist ein zentraler Baum.

Problem 2

Finden Sie das Zentrum / Bi-Zentrum des folgenden Baums heraus -

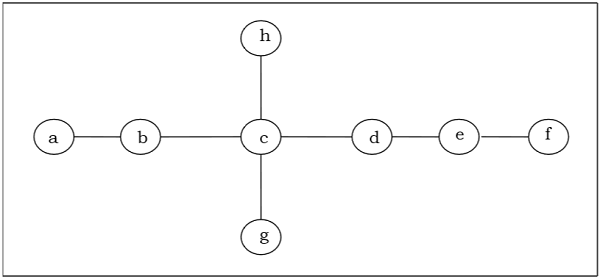
Solution

Zuerst entfernen wir alle Eckpunkte des Grades 1 und entfernen auch ihre einfallenden Kanten und erhalten den folgenden Baum -

Wieder werden wir alle Eckpunkte des Grades 1 entfernen und auch ihre einfallenden Kanten entfernen und den folgenden Baum erhalten -

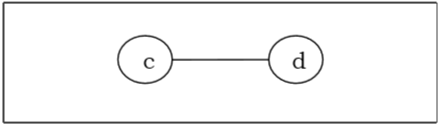
Schließlich haben wir noch zwei Eckpunkte 'c' und 'd' übrig, daher stoppen wir den Algorithmus. Da zwei Eckpunkte, die durch eine Kante verbunden sind, übrig bleiben, hat dieser Baum eine zweizentrische 'cd' und der Baum ist zweizentrisch.

Beschriftete Bäume

Definition- Ein beschrifteter Baum ist ein Baum, dessen Eckpunkte eindeutige Zahlen von 1 bis n erhalten. Wir können solche Bäume für kleine Werte von n von Hand zählen, um eine allgemeine Formel zu vermuten. Die Anzahl der markierten Bäume mit n Eckpunkten beträgt $ n ^ {n-2} $. Zwei beschriftete Bäume sind isomorph, wenn ihre Diagramme isomorph sind und die entsprechenden Punkte der beiden Bäume die gleichen Beschriftungen haben.

Beispiel

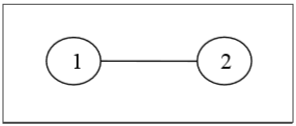
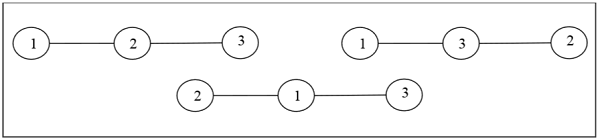
Unbeschriftete Bäume

Definition- Ein unbeschrifteter Baum ist ein Baum, dessen Eckpunkte keine Nummern erhalten. Die Anzahl der markierten Bäume mit n Eckpunkten beträgt $ \ frac {(2n)!} {(N + 1)! N! } $ (n- ^te katalanische Nummer)

Beispiel

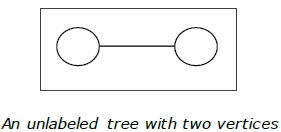
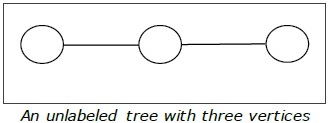
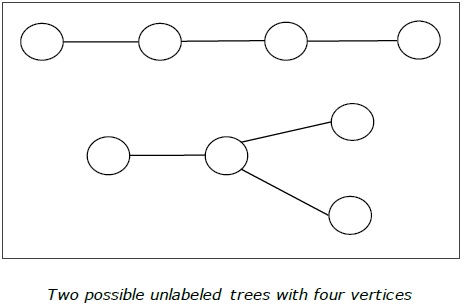
Verwurzelter Baum

Ein Wurzelbaum $ G $ ist ein verbundener azyklischer Graph mit einem speziellen Knoten, der als Wurzel des Baums bezeichnet wird und jede Kante direkt oder indirekt von der Wurzel stammt. Ein geordneter Wurzelbaum ist ein Wurzelbaum, in dem die untergeordneten Elemente jedes internen Scheitelpunkts geordnet sind. Wenn jeder interne Scheitelpunkt eines Wurzelbaums nicht mehr als m Kinder hat, spricht man von einem Baum. Wenn jeder interne Scheitelpunkt eines Wurzelbaums genau m Kinder hat, wird er als vollständiger Baum bezeichnet. Wenn $ m = 2 $ ist, wird der Wurzelbaum als Binärbaum bezeichnet.

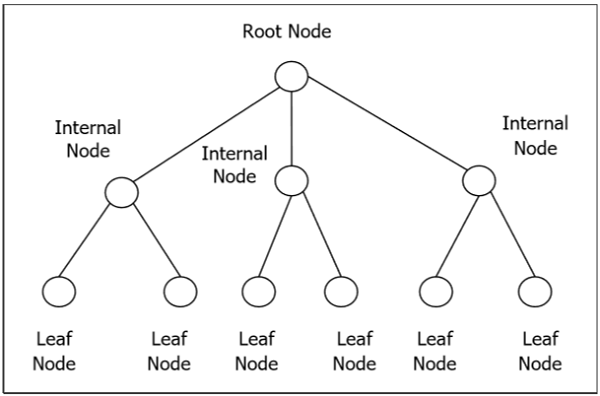
Binärer Suchbaum

Der binäre Suchbaum ist ein binärer Baum, der die folgende Eigenschaft erfüllt:

$ X $ im linken Unterbaum des Scheitelpunkts $ V, Wert (X) \ le Wert (V) $
$ Y $ im rechten Teilbaum des Scheitelpunkts $ V, Wert (Y) \ ge Wert (V) $

Der Wert aller Eckpunkte des linken Teilbaums eines internen Knotens $ V $ ist also kleiner oder gleich $ V $ und der Wert aller Eckpunkte des rechten Teilbaums des internen Knotens $ V $ sind größer oder gleich $ V $. Die Anzahl der Links vom Stammknoten zum tiefsten Knoten entspricht der Höhe des binären Suchbaums.

Beispiel

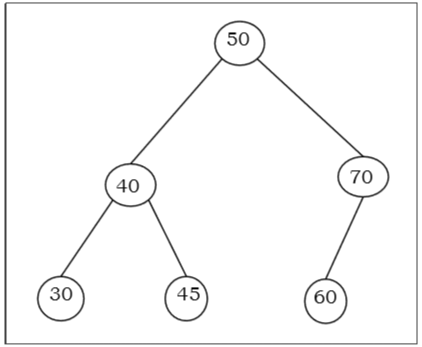
Algorithmus zur Suche nach einem Schlüssel in BST

BST_Search(x, k) 
if ( x = NIL or k = Value[x] ) 
   return x; 
if ( k < Value[x]) 
   return BST_Search (left[x], k); 
else  
   return BST_Search (right[x], k)

Komplexität des binären Suchbaums

	Durchschnittlicher Fall	Schlimmsten Fall
Raumkomplexität	Auf)	Auf)
Komplexität der Suche	O (log n)	Auf)
Einfügekomplexität	O (log n)	Auf)
Löschkomplexität	O (log n)	Auf)