Diskrete Mathematik - Kurzanleitung

Mathematik kann grob in zwei Kategorien eingeteilt werden -

• Continuous Mathematics- Es basiert auf einer durchgehenden Zahlenlinie oder den reellen Zahlen. Es zeichnet sich dadurch aus, dass zwischen zwei beliebigen Zahlen fast immer unendlich viele Zahlen stehen. Beispielsweise kann eine Funktion in der kontinuierlichen Mathematik in einer glatten Kurve ohne Unterbrechungen dargestellt werden.

• Discrete Mathematics- Es beinhaltet unterschiedliche Werte; dh zwischen zwei beliebigen Punkten gibt es eine zählbare Anzahl von Punkten. Wenn wir beispielsweise eine endliche Menge von Objekten haben, kann die Funktion als Liste geordneter Paare mit diesen Objekten definiert und als vollständige Liste dieser Paare dargestellt werden.

Themen in der diskreten Mathematik

Obwohl es keine bestimmte Anzahl von Zweigen der diskreten Mathematik geben kann, werden die folgenden Themen in jeder diesbezüglichen Studie fast immer behandelt:

• Mengen, Beziehungen und Funktionen
• Mathematische Logik
• Gruppentheorie
• Zähltheorie
• Probability
• Mathematische Induktions- und Wiederholungsbeziehungen
• Graphentheorie
• Trees
• Boolsche Algebra

Wir werden jedes dieser Konzepte in den folgenden Kapiteln dieses Tutorials diskutieren.

Deutscher Mathematiker G. Cantorführte das Konzept der Mengen ein. Er hatte eine Menge als eine Sammlung bestimmter und unterscheidbarer Objekte definiert, die anhand bestimmter Regeln oder Beschreibungen ausgewählt wurden.

SetDie Theorie bildet die Grundlage für mehrere andere Studienbereiche wie Zähltheorie, Beziehungen, Graphentheorie und Finite-State-Maschinen. In diesem Kapitel werden wir die verschiedenen Aspekte von behandelnSet Theory.

Set - Definition

Ein Set ist eine ungeordnete Sammlung verschiedener Elemente. Ein Set kann explizit geschrieben werden, indem seine Elemente mit der Set-Klammer aufgelistet werden. Wenn die Reihenfolge der Elemente geändert oder ein Element einer Menge wiederholt wird, werden keine Änderungen an der Menge vorgenommen.

Ein Beispiel für Sets

• Eine Menge aller positiven ganzen Zahlen
• Eine Reihe aller Planeten im Sonnensystem
• Eine Reihe aller Staaten in Indien
• Ein Satz aller Kleinbuchstaben des Alphabets

Darstellung eines Sets

Sets können auf zwei Arten dargestellt werden:

• Dienstplan oder Tabellenform
• Legen Sie die Builder-Notation fest

Dienstplan oder Tabellenform

Die Menge wird dargestellt, indem alle Elemente aufgelistet werden, aus denen sie besteht. Die Elemente sind in geschweiften Klammern eingeschlossen und durch Kommas getrennt.

Example 1 - Vokalsatz im englischen Alphabet, $A = \lbrace a,e,i,o,u \rbrace$

Example 2 - Satz ungerader Zahlen unter 10, $B = \lbrace 1,3,5,7,9 \rbrace$

Legen Sie die Builder-Notation fest

Die Menge wird definiert, indem eine Eigenschaft angegeben wird, die Elemente der Menge gemeinsam haben. Das Set wird beschrieben als$A = \lbrace x : p(x) \rbrace$

Example 1 - Das Set $\lbrace a,e,i,o,u \rbrace$ ist geschrieben als -

$A = \lbrace x : \text{x is a vowel in English alphabet} \rbrace$

Example 2 - Das Set $\lbrace 1,3,5,7,9 \rbrace$ ist geschrieben als -

$B = \lbrace x : 1 \le x \lt 10 \ and\ (x \% 2) \ne 0 \rbrace$

Wenn ein Element x Mitglied einer Menge S ist, wird es mit bezeichnet $x \in S$ und wenn ein Element y kein Mitglied der Menge S ist, wird es mit bezeichnet $y \notin S$.

Example- Wenn$S = \lbrace1, 1.2, 1.7, 2\rbrace , 1 \in S$ aber $1.5 \notin S$

Einige wichtige Sätze

N - die Menge aller natürlichen Zahlen = $\lbrace1, 2, 3, 4, .....\rbrace$

Z - die Menge aller ganzen Zahlen = $\lbrace....., -3, -2, -1, 0, 1, 2, 3, .....\rbrace$

Z⁺ - die Menge aller positiven ganzen Zahlen

Q - die Menge aller rationalen Zahlen

R - die Menge aller reellen Zahlen

W - die Menge aller ganzen Zahlen

Kardinalität einer Menge

Kardinalität einer Menge S, bezeichnet mit $|S|$ist die Anzahl der Elemente der Menge. Die Nummer wird auch als Kardinalnummer bezeichnet. Wenn eine Menge unendlich viele Elemente hat, ist ihre Kardinalität$\infty$.

Example - - $|\lbrace 1, 4, 3, 5 \rbrace | = 4, | \lbrace 1, 2, 3, 4, 5, \dots \rbrace | = \infty$

Wenn es zwei Sätze X und Y gibt,

• $|X| = |Y|$bezeichnet zwei Sätze X und Y mit derselben Kardinalität. Es tritt auf, wenn die Anzahl der Elemente in X genau der Anzahl der Elemente in Y entspricht. In diesem Fall existiert eine bijektive Funktion 'f' von X nach Y.

• $|X| \le |Y|$bedeutet, dass die Kardinalität von Satz X kleiner oder gleich der Kardinalität von Satz Y ist. Es tritt auf, wenn die Anzahl der Elemente in X kleiner oder gleich der von Y ist. Hier existiert eine Injektionsfunktion 'f' von X nach Y.

• $|X| \lt |Y|$bedeutet, dass die Kardinalität von Satz X geringer ist als die Kardinalität von Satz Y. Es tritt auf, wenn die Anzahl der Elemente in X kleiner als die von Y ist. Hier ist die Funktion 'f' von X nach Y eine injektive Funktion, aber keine bijektive.

• $If\ |X| \le |Y|$ und $|X| \ge |Y|$ dann $|X| = |Y|$. Die Mengen X und Y werden üblicherweise als äquivalente Mengen bezeichnet.

Arten von Sets

Sets können in viele Typen eingeteilt werden. Einige davon sind endlich, unendlich, Teilmenge, universell, richtig, Singleton-Menge usw.

Endliche Menge

Eine Menge, die eine bestimmte Anzahl von Elementen enthält, wird als endliche Menge bezeichnet.

Example - - $S = \lbrace x \:| \:x \in N$ und $70 \gt x \gt 50 \rbrace$

Unendliches Set

Eine Menge, die unendlich viele Elemente enthält, wird als unendliche Menge bezeichnet.

Example - - $S = \lbrace x \: | \: x \in N $ und $ x \gt 10 \rbrace$

Teilmenge

Eine Menge X ist eine Teilmenge der Menge Y (geschrieben als $X \subseteq Y$) wenn jedes Element von X ein Element der Menge Y ist.

Example 1 - Lassen Sie, $X = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ und $Y = \lbrace 1, 2 \rbrace$. Hier ist Menge Y eine Teilmenge von Menge X, da sich alle Elemente von Menge Y in Menge X befinden. Daher können wir schreiben$Y \subseteq X$.

Example 2 - Lassen Sie, $X = \lbrace 1, 2, 3 \rbrace$ und $Y = \lbrace 1, 2, 3 \rbrace$. Hier ist Menge Y eine Teilmenge (keine richtige Teilmenge) von Menge X, da sich alle Elemente von Menge Y in Menge X befinden. Daher können wir schreiben$Y \subseteq X$.

Echte Teilmenge

Der Begriff "richtige Teilmenge" kann als "Teilmenge von, aber nicht gleich" definiert werden. Eine Menge X ist eine richtige Teilmenge der Menge Y (geschrieben als$ X \subset Y $) wenn jedes Element von X ein Element der Menge Y und ist $|X| \lt |Y|$.

Example - Lassen Sie, $X = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ und $Y = \lbrace 1, 2 \rbrace$. Hier eingestellt$Y \subset X$ da alle elemente in $Y$ sind enthalten in $X$ auch und $X$ hat mindestens ein Element ist mehr als gesetzt $Y$.

Universelles Set

Es ist eine Sammlung aller Elemente in einem bestimmten Kontext oder einer bestimmten Anwendung. Alle Mengen in diesem Kontext oder in dieser Anwendung sind im Wesentlichen Teilmengen dieser universellen Menge. Universalsätze werden als dargestellt$U$.

Example - Wir können definieren $U$als die Menge aller Tiere auf Erden. In diesem Fall ist die Menge aller Säugetiere eine Teilmenge von$U$, Menge aller Fische ist eine Teilmenge von $U$, Menge aller Insekten ist eine Teilmenge von $U$, und so weiter.

Leerer Satz oder Nullsatz

Ein leerer Satz enthält keine Elemente. Es wird mit bezeichnet$\emptyset$. Da die Anzahl der Elemente in einer leeren Menge endlich ist, ist die leere Menge eine endliche Menge. Die Kardinalität der leeren Menge oder der Nullmenge ist Null.

Example - - $S = \lbrace x \:| \: x \in N$ und $7 \lt x \lt 8 \rbrace = \emptyset$

Singleton Set oder Unit Set

Singleton-Set oder Unit-Set enthält nur ein Element. Eine Singleton-Menge wird mit bezeichnet$\lbrace s \rbrace$.

Example - - $S = \lbrace x \:| \:x \in N,\ 7 \lt x \lt 9 \rbrace$ = $\lbrace 8 \rbrace$

Gleicher Satz

Wenn zwei Mengen dieselben Elemente enthalten, werden sie als gleich bezeichnet.

Example - Wenn $A = \lbrace 1, 2, 6 \rbrace$ und $B = \lbrace 6, 1, 2 \rbrace$sind sie gleich, da jedes Element der Menge A ein Element der Menge B ist und jedes Element der Menge B ein Element der Menge A ist.

Äquivalenter Satz

Wenn die Kardinalitäten zweier Mengen gleich sind, werden sie als äquivalente Mengen bezeichnet.

Example - Wenn $A = \lbrace 1, 2, 6 \rbrace$ und $B = \lbrace 16, 17, 22 \rbrace$sind sie äquivalent, da die Kardinalität von A gleich der Kardinalität von B ist, dh $|A| = |B| = 3$

Überlappender Satz

Zwei Mengen mit mindestens einem gemeinsamen Element werden als überlappende Mengen bezeichnet.

Bei überlappenden Mengen -

• $n(A \cup B) = n(A) + n(B) - n(A \cap B)$

• $n(A \cup B) = n(A - B) + n(B - A) + n(A \cap B)$

• $n(A) = n(A - B) + n(A \cap B)$

• $n(B) = n(B - A) + n(A \cap B)$

Example - Lassen Sie, $A = \lbrace 1, 2, 6 \rbrace$ und $B = \lbrace 6, 12, 42 \rbrace$. Es gibt ein gemeinsames Element '6', daher sind diese Mengen überlappende Mengen.

Disjunktes Set

Zwei Mengen A und B werden disjunkte Mengen genannt, wenn sie nicht einmal ein Element gemeinsam haben. Daher haben disjunkte Mengen die folgenden Eigenschaften:

• $n(A \cap B) = \emptyset$

• $n(A \cup B) = n(A) + n(B)$

Example - Lassen Sie, $A = \lbrace 1, 2, 6 \rbrace$ und $B = \lbrace 7, 9, 14 \rbrace$gibt es kein einziges gemeinsames Element, daher sind diese Mengen überlappende Mengen.

Venn-Diagramme

Das 1880 von John Venn erfundene Venn-Diagramm ist ein schematisches Diagramm, das alle möglichen logischen Beziehungen zwischen verschiedenen mathematischen Mengen zeigt.

Examples

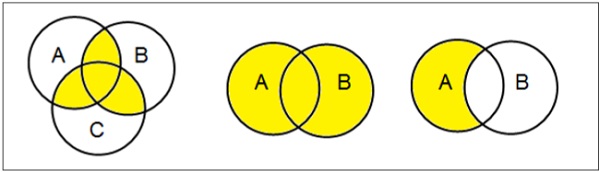
Operationen einstellen

Zu den Set-Operationen gehören Set Union, Set Intersection, Set Difference, Complement of Set und Cartesian Product.

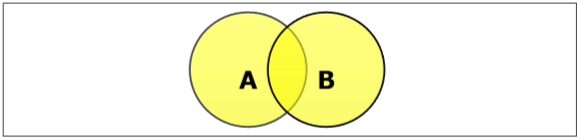
Set Union

Die Vereinigung der Mengen A und B (bezeichnet mit $A \cup B$) ist die Menge von Elementen, die sich in A, in B oder sowohl in A als auch in B befinden. $A \cup B = \lbrace x \:| \: x \in A\ OR\ x \in B \rbrace$.

Example - Wenn $A = \lbrace 10, 11, 12, 13 \rbrace$ und B = $\lbrace 13, 14, 15 \rbrace$, dann $A \cup B = \lbrace 10, 11, 12, 13, 14, 15 \rbrace$. (Das gemeinsame Element kommt nur einmal vor)

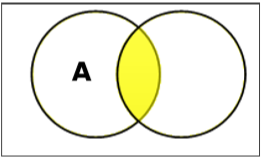
Schnittpunkt einstellen

Der Schnittpunkt der Mengen A und B (bezeichnet mit $A \cap B$) ist die Menge der Elemente, die sich sowohl in A als auch in B befinden. $A \cap B = \lbrace x \:|\: x \in A\ AND\ x \in B \rbrace$.

Example - Wenn $A = \lbrace 11, 12, 13 \rbrace$ und $B = \lbrace 13, 14, 15 \rbrace$, dann $A \cap B = \lbrace 13 \rbrace$.

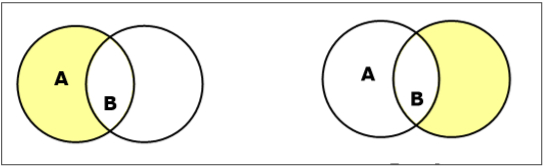
Differenz / relative Ergänzung einstellen

Die Mengenunterschiede der Mengen A und B (bezeichnet mit $A – B$) ist die Menge von Elementen, die nur in A, aber nicht in B sind. $A - B = \lbrace x \:| \: x \in A\ AND\ x \notin B \rbrace$.

Example - Wenn $A = \lbrace 10, 11, 12, 13 \rbrace$ und $B = \lbrace 13, 14, 15 \rbrace$, dann $(A - B) = \lbrace 10, 11, 12 \rbrace$ und $(B - A) = \lbrace 14, 15 \rbrace$. Hier können wir sehen$(A - B) \ne (B - A)$

Ergänzung eines Sets

Das Komplement einer Menge A (bezeichnet mit $A’$) ist die Menge von Elementen, die nicht in Menge A enthalten sind. $A' = \lbrace x | x \notin A \rbrace$.

Genauer, $A'= (U - A)$ wo $U$ ist eine universelle Menge, die alle Objekte enthält.

Example - Wenn $A = \lbrace x \:| \: x\ \: {belongs\: to\: set\: of\: odd \:integers} \rbrace$ dann $A' = \lbrace y\: | \: y\ \: {does\: not\: belong\: to\: set\: of\: odd\: integers } \rbrace$

Kartesisches Produkt / Kreuzprodukt

Das kartesische Produkt aus n Mengen $A_1, A_2, \dots A_n$ bezeichnet als $A_1 \times A_2 \dots \times A_n$ kann als alle möglichen geordneten Paare definiert werden $(x_1, x_2, \dots x_n)$ wo $x_1 \in A_1, x_2 \in A_2, \dots x_n \in A_n$

Example - Wenn wir zwei Sätze nehmen $A = \lbrace a, b \rbrace$ und $B = \lbrace 1, 2 \rbrace$,

Das kartesische Produkt von A und B ist geschrieben als - $A \times B = \lbrace (a, 1), (a, 2), (b, 1), (b, 2)\rbrace$

Das kartesische Produkt von B und A ist geschrieben als - $B \times A = \lbrace (1, a), (1, b), (2, a), (2, b)\rbrace$

Power Set

Potenzmenge einer Menge S ist die Menge aller Teilmengen von S einschließlich der leeren Menge. Die Kardinalität einer Potenzmenge einer Menge S der Kardinalität n ist$2^n$. Die eingestellte Leistung wird als bezeichnet$P(S)$.

Example −

Für einen Satz $S = \lbrace a, b, c, d \rbrace$ Berechnen wir die Teilmengen -

• Teilmengen mit 0 Elementen - $\lbrace \emptyset \rbrace$ (der leere Satz)

• Teilmengen mit 1 Element - $\lbrace a \rbrace, \lbrace b \rbrace, \lbrace c \rbrace, \lbrace d \rbrace$

• Teilmengen mit 2 Elementen - $\lbrace a, b \rbrace, \lbrace a,c \rbrace, \lbrace a, d \rbrace, \lbrace b, c \rbrace, \lbrace b,d \rbrace,\lbrace c,d \rbrace$

• Teilmengen mit 3 Elementen - $\lbrace a ,b, c\rbrace,\lbrace a, b, d \rbrace, \lbrace a,c,d \rbrace,\lbrace b,c,d \rbrace$

• Teilmengen mit 4 Elementen - $\lbrace a, b, c, d \rbrace$

Daher, $P(S)=$

$\lbrace \quad \lbrace \emptyset \rbrace, \lbrace a \rbrace, \lbrace b \rbrace, \lbrace c \rbrace, \lbrace d \rbrace, \lbrace a,b \rbrace, \lbrace a,c \rbrace, \lbrace a,d \rbrace, \lbrace b,c \rbrace, \lbrace b,d \rbrace, \lbrace c,d \rbrace, \lbrace a,b,c \rbrace, \lbrace a,b,d \rbrace, \lbrace a,c,d \rbrace, \lbrace b,c,d \rbrace, \lbrace a,b,c,d \rbrace \quad \rbrace$

$| P(S) | = 2^4 = 16$

Note - Der Energiesatz eines leeren Satzes ist ebenfalls ein leerer Satz.

$| P (\lbrace \emptyset \rbrace) | = 2^0 = 1$

Partitionierung eines Sets

Die Partition einer Menge, beispielsweise S , ist beispielsweise eine Sammlung von n disjunkten Teilmengen$P_1, P_2, \dots P_n$ das erfüllt die folgenden drei Bedingungen -

• $P_i$ enthält nicht die leere Menge.

  $\lbrack P_i \ne \lbrace \emptyset \rbrace\ for\ all\ 0 \lt i \le n \rbrack$

• Die Vereinigung der Teilmengen muss der gesamten ursprünglichen Menge entsprechen.

  $\lbrack P_1 \cup P_2 \cup \dots \cup P_n = S \rbrack$

• Der Schnittpunkt zweier unterschiedlicher Mengen ist leer.

  $\lbrack P_a \cap P_b = \lbrace \emptyset \rbrace,\ for\ a \ne b\ where\ n \ge a,\: b \ge 0 \rbrack$

Example

Lassen $S = \lbrace a, b, c, d, e, f, g, h \rbrace$

Eine wahrscheinliche Partitionierung ist $\lbrace a \rbrace, \lbrace b, c, d \rbrace, \lbrace e, f, g, h \rbrace$

Eine andere wahrscheinliche Partitionierung ist $\lbrace a, b \rbrace, \lbrace c, d \rbrace, \lbrace e, f, g, h \rbrace$

Glockennummern

Glockennummern geben die Anzahl der Möglichkeiten an, eine Menge zu partitionieren. Sie sind mit gekennzeichnet$B_n$ Dabei ist n die Kardinalität der Menge.

Example - -

Lassen $S = \lbrace 1, 2, 3\rbrace$, $n = |S| = 3$

Die alternativen Partitionen sind -

1. $\emptyset , \lbrace 1, 2, 3 \rbrace$

2. $\lbrace 1 \rbrace , \lbrace 2, 3 \rbrace$

3. $\lbrace 1, 2 \rbrace , \lbrace 3 \rbrace$

4. $\lbrace 1, 3 \rbrace , \lbrace 2 \rbrace$

5. $\lbrace 1 \rbrace , \lbrace 2 \rbrace , \lbrace 3 \rbrace$

Daher $B_3 = 5$

Wann immer Mengen diskutiert werden, ist die Beziehung zwischen den Elementen der Mengen das nächste, was auftaucht. Relations kann zwischen Objekten derselben Menge oder zwischen Objekten von zwei oder mehr Mengen existieren.

Definition und Eigenschaften

Eine binäre Beziehung R von der Menge x zu y (geschrieben als $xRy$ oder $R(x,y)$) ist eine Teilmenge des kartesischen Produkts $x \times y$. Wenn das geordnete Paar von G umgekehrt wird, ändert sich auch die Beziehung.

Im Allgemeinen eine n-fache Beziehung R zwischen Mengen $A_1, \dots ,\ and\ A_n$ ist eine Teilmenge des n-ary-Produkts $A_1 \times \dots \times A_n$. Die minimale Kardinalität einer Beziehung R ist Null und das Maximum ist$n^2$ in diesem Fall.

Eine binäre Beziehung R auf einer einzelnen Menge A ist eine Teilmenge von $A \times A$.

Für zwei unterschiedliche Mengen A und B mit den Kardinalitäten m bzw. n beträgt die maximale Kardinalität einer Beziehung R von A nach B mn .

Domäne und Reichweite

Wenn es zwei Mengen A und B gibt und die Beziehung R ein Ordnungspaar (x, y) hat, dann -

• Das domain von R ist Dom (R) die Menge $\lbrace x \:| \: (x, y) \in R \:for\: some\: y\: in\: B \rbrace$

• Das range von R ist Ran (R) die Menge $\lbrace y\: |\: (x, y) \in R \:for\: some\: x\: in\: A\rbrace$

Beispiele

Lassen, $A = \lbrace 1, 2, 9 \rbrace $ und $ B = \lbrace 1, 3, 7 \rbrace$

• Fall 1 - Wenn die Beziehung R 'gleich' ist, dann $R = \lbrace (1, 1), (3, 3) \rbrace$

  Dom (R) = $\lbrace 1, 3 \rbrace , Ran(R) = \lbrace 1, 3 \rbrace$

• Fall 2 - Wenn die Beziehung R 'kleiner als' ist, dann $R = \lbrace (1, 3), (1, 7), (2, 3), (2, 7) \rbrace$

  Dom (R) = $\lbrace 1, 2 \rbrace , Ran(R) = \lbrace 3, 7 \rbrace$

• Fall 3 - Wenn die Beziehung R 'größer als' ist, dann $R = \lbrace (2, 1), (9, 1), (9, 3), (9, 7) \rbrace$

  Dom (R) = $\lbrace 2, 9 \rbrace , Ran(R) = \lbrace 1, 3, 7 \rbrace$

Darstellung von Beziehungen mit Graph

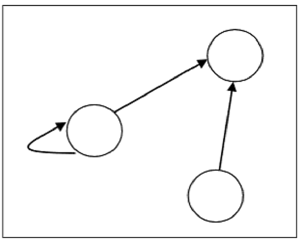
Eine Beziehung kann mithilfe eines gerichteten Graphen dargestellt werden.

Die Anzahl der Eckpunkte im Diagramm entspricht der Anzahl der Elemente in der Menge, aus denen die Beziehung definiert wurde. Für jedes geordnete Paar (x, y) in der Beziehung R gibt es eine gerichtete Kante vom Scheitelpunkt 'x' zum Scheitelpunkt 'y'. Wenn es ein geordnetes Paar (x, x) gibt, gibt es eine Selbstschleife am Scheitelpunkt 'x'.

Angenommen, es gibt eine Beziehung $R = \lbrace (1, 1), (1,2), (3, 2) \rbrace$ am Set $S = \lbrace 1, 2, 3 \rbrace$kann es durch die folgende Grafik dargestellt werden -

Arten von Beziehungen

• Das Empty Relation zwischen den Sätzen X und Y oder auf E ist der leere Satz $\emptyset$

• Das Full Relation zwischen den Sätzen X und Y ist der Satz $X \times Y$

• Das Identity Relation am Satz X ist der Satz $\lbrace (x, x) | x \in X \rbrace$

• Die inverse Beziehung R 'einer Beziehung R ist definiert als - $R' = \lbrace (b, a) | (a, b) \in R \rbrace$

  Example - Wenn $R = \lbrace (1, 2), (2, 3) \rbrace$ dann $R' $ wird sein $\lbrace (2, 1), (3, 2) \rbrace$

• Eine Beziehung R auf Satz A wird aufgerufen Reflexive wenn $\forall a \in A$ ist verwandt mit a (aRa gilt)

  Example - Die Beziehung $R = \lbrace (a, a), (b, b) \rbrace$ am Set $X = \lbrace a, b \rbrace$ ist reflexiv.

• Eine Beziehung R auf Satz A wird aufgerufen Irreflexive wenn nein $a \in A$ ist verwandt mit a (aRa gilt nicht).

  Example - Die Beziehung $R = \lbrace (a, b), (b, a) \rbrace$ am Set $X = \lbrace a, b \rbrace$ ist irreflexiv.

• Eine Beziehung R auf Satz A wird aufgerufen Symmetric wenn $xRy$ impliziert $yRx$, $\forall x \in A$ und $\forall y \in A$.

  Example - Die Beziehung $R = \lbrace (1, 2), (2, 1), (3, 2), (2, 3) \rbrace$ am Set $A = \lbrace 1, 2, 3 \rbrace$ ist symmetrisch.

• Eine Beziehung R auf Satz A wird aufgerufen Anti-Symmetric wenn $xRy$ und $yRx$ impliziert $x = y \: \forall x \in A$ und $\forall y \in A$.

  Example - Die Beziehung $R = \lbrace (x, y)\to N |\:x \leq y \rbrace$ ist da antisymmetrisch $x \leq y$ und $y \leq x$ impliziert $x = y$.

• Eine Beziehung R auf Satz A wird aufgerufen Transitive wenn $xRy$ und $yRz$ impliziert $xRz, \forall x,y,z \in A$.

  Example - Die Beziehung $R = \lbrace (1, 2), (2, 3), (1, 3) \rbrace$ am Set $A = \lbrace 1, 2, 3 \rbrace$ ist transitiv.

• Eine Beziehung ist eine Equivalence Relation wenn es reflexiv, symmetrisch und transitiv ist.

  Example - Die Beziehung $R = \lbrace (1, 1), (2, 2), (3, 3), (1, 2), (2,1), (2,3), (3,2), (1,3), (3,1) \rbrace$ am Set $A = \lbrace 1, 2, 3 \rbrace$ ist eine Äquivalenzbeziehung, da sie reflexiv, symmetrisch und transitiv ist.

EIN FunctionWeist jedem Element einer Menge genau ein Element einer verwandten Menge zu. Funktionen finden ihre Anwendung in verschiedenen Bereichen wie der Darstellung der rechnerischen Komplexität von Algorithmen, dem Zählen von Objekten, dem Studium von Sequenzen und Zeichenfolgen, um nur einige zu nennen. Das dritte und letzte Kapitel dieses Teils beleuchtet die wichtigen Aspekte von Funktionen.

Funktion - Definition

Eine Funktion oder Zuordnung (definiert als $f: X \rightarrow Y$) ist eine Beziehung von Elementen einer Menge X zu Elementen einer anderen Menge Y (X und Y sind nicht leere Mengen). X heißt Domain und Y heißt Codomain der Funktion 'f'.

Die Funktion 'f' ist eine Beziehung auf X und Y, so dass für jede $x \in X$gibt es eine einzigartige $y \in Y$ so dass $(x,y) \in R$. 'x' heißt Vorbild und 'y' heißt Bild der Funktion f.

Eine Funktion kann eins zu eins oder viele zu eins sein, aber nicht eins zu viele.

Injective / Eins-zu-Eins-Funktion

Eine Funktion $f: A \rightarrow B$ ist injektive oder Eins-zu-Eins-Funktion, wenn für jeden $b \in B$gibt es höchstens einen $a \in A$ so dass $f(s) = t$.

Dies bedeutet eine Funktion f ist injektiv, wenn $a_1 \ne a_2$ impliziert $f(a1) \ne f(a2)$.

Beispiel

• $f: N \rightarrow N, f(x) = 5x$ ist injektiv.

• $f: N \rightarrow N, f(x) = x^2$ ist injektiv.

• $f: R\rightarrow R, f(x) = x^2$ ist nicht injektiv als $(-x)^2 = x^2$

Surjektiv / Auf Funktion

Eine Funktion $f: A \rightarrow B$ist surjektiv (auf), wenn das Bild von f seinem Bereich entspricht. Gleichermaßen für jeden$b \in B$gibt es einige $a \in A$ so dass $f(a) = b$. Dies bedeutet, dass für jedes y in B ein x in A existiert, so dass$y = f(x)$.

Beispiel

• $f : N \rightarrow N, f(x) = x + 2$ ist surjektiv.

• $f : R \rightarrow R, f(x) = x^2$ ist nicht surjektiv, da wir keine reelle Zahl finden können, deren Quadrat negativ ist.

Bijektiv / Eins-zu-eins-Korrespondent

Eine Funktion $f: A \rightarrow B$ ist genau dann bijektiv oder Eins-zu-eins-Korrespondent, wenn f ist sowohl injektiv als auch surjektiv.

Problem

Beweisen Sie, dass eine Funktion $f: R \rightarrow R$ definiert von $f(x) = 2x – 3$ ist eine bijektive Funktion.

Explanation - Wir müssen beweisen, dass diese Funktion sowohl injektiv als auch surjektiv ist.

Wenn $f(x_1) = f(x_2)$, dann $2x_1 – 3 = 2x_2 – 3 $ und das impliziert es $x_1 = x_2$.

Daher ist f injective.

Hier, $2x – 3= y$

Damit, $x = (y+5)/3$ welches zu R und gehört $f(x) = y$.

Daher ist f surjective.

Schon seit f ist beides surjective und injective, Wir können sagen f ist bijective.

Inverse einer Funktion

Das inverse einer eins zu eins entsprechenden Funktion $f : A \rightarrow B$ist die Funktion $g : B \rightarrow A$, hält die folgende Eigenschaft -

$f(x) = y \Leftrightarrow g(y) = x$

Die Funktion f wird aufgerufen invertible, wenn seine Umkehrfunktion g existiert.

Beispiel

• Eine Funktion $f : Z \rightarrow Z, f(x)=x+5$ist invertierbar, da es die Umkehrfunktion hat $ g : Z \rightarrow Z, g(x)= x-5$.

• Eine Funktion $f : Z \rightarrow Z, f(x)=x^2$ ist nicht umkehrbar, da dies nicht eins zu eins ist als $(-x)^2=x^2$.

Zusammensetzung der Funktionen

Zwei Funktionen $f: A \rightarrow B$ und $g: B \rightarrow C$ kann zu einer Komposition zusammengesetzt werden $g o f$. Dies ist eine Funktion von A bis C, definiert durch$(gof)(x) = g(f(x))$

Beispiel

Lassen $f(x) = x + 2$ und $g(x) = 2x + 1$, finden $( f o g)(x)$ und $( g o f)(x)$.

Lösung

$(f o g)(x) = f (g(x)) = f(2x + 1) = 2x + 1 + 2 = 2x + 3$

$(g o f)(x) = g (f(x)) = g(x + 2) = 2 (x+2) + 1 = 2x + 5$

Daher, $(f o g)(x) \neq (g o f)(x)$

Einige Fakten zur Zusammensetzung

• Wenn f und g eins zu eins sind, dann die Funktion $(g o f)$ ist auch eins zu eins.

• Wenn f und g eingeschaltet sind, dann die Funktion $(g o f)$ ist auch auf.

• Die Zusammensetzung enthält immer assoziative Eigenschaften, jedoch keine kommutativen Eigenschaften.

Die Regeln der mathematischen Logik spezifizieren Methoden zum Denken mathematischer Aussagen. Der griechische Philosoph Aristoteles war der Pionier des logischen Denkens. Das logische Denken bildet die theoretische Grundlage für viele Bereiche der Mathematik und damit der Informatik. Es hat viele praktische Anwendungen in der Informatik wie das Design von Rechenmaschinen, künstliche Intelligenz, die Definition von Datenstrukturen für Programmiersprachen usw.

Propositional Logicbefasst sich mit Aussagen, denen die Wahrheitswerte „wahr“ und „falsch“ zugeordnet werden können. Ziel ist es, diese Aussagen entweder einzeln oder zusammengesetzt zu analysieren.

Präpositionale Logik - Definition

Ein Satz ist eine Sammlung deklarativer Aussagen, die entweder einen Wahrheitswert "wahr" oder einen Wahrheitswert "falsch" haben. Ein Satz besteht aus Satzvariablen und Konnektiven. Wir bezeichnen die Satzvariablen mit Großbuchstaben (A, B usw.). Die Konnektive verbinden die Satzvariablen.

Einige Beispiele für Vorschläge sind unten angegeben -

• "Man is Mortal" gibt den Wahrheitswert "TRUE" zurück.
• "12 + 9 = 3 - 2" gibt den Wahrheitswert "FALSE" zurück.

Das Folgende ist kein Vorschlag -

• "A ist kleiner als 2". Dies liegt daran, dass wir nicht sagen können, ob die Aussage wahr oder falsch ist, es sei denn, wir geben einen bestimmten Wert von A an.

Konnektiva

In der Aussagenlogik verwenden wir im Allgemeinen fünf Konnektive, die -

• ODER ($\lor$)

• UND ($\land$)

• Negation / NICHT ($\lnot$)

• Implikation / wenn-dann ($\rightarrow$)

• Dann und nur dann, wenn ($\Leftrightarrow$).

OR ($\lor$) - Die ODER-Verknüpfung zweier Sätze A und B (geschrieben als $A \lor B$) ist wahr, wenn mindestens eine der Satzvariablen A oder B wahr ist.

Die Wahrheitstabelle lautet wie folgt:

EIN	B.	A ∨ B.
Wahr	Wahr	Wahr
Wahr	Falsch	Wahr
Falsch	Wahr	Wahr
Falsch	Falsch	Falsch

AND ($\land$) - Die UND-Verknüpfung zweier Sätze A und B (geschrieben als $A \land B$) ist wahr, wenn sowohl die Satzvariable A als auch B wahr sind.

Die Wahrheitstabelle lautet wie folgt:

EIN	B.	A ∧ B.
Wahr	Wahr	Wahr
Wahr	Falsch	Falsch
Falsch	Wahr	Falsch
Falsch	Falsch	Falsch

Negation ($\lnot$) - Die Negation eines Satzes A (geschrieben als $\lnot A$) ist falsch, wenn A wahr ist, und ist wahr, wenn A falsch ist.

Die Wahrheitstabelle lautet wie folgt:

EIN	¬ A.
Wahr	Falsch
Falsch	Wahr

Implication / if-then ($\rightarrow$) - Eine Implikation $A \rightarrow B$ist der Satz "wenn A, dann B". Es ist falsch, wenn A wahr und B falsch ist. Die übrigen Fälle sind wahr.

Die Wahrheitstabelle lautet wie folgt:

EIN	B.	A → B.
Wahr	Wahr	Wahr
Wahr	Falsch	Falsch
Falsch	Wahr	Wahr
Falsch	Falsch	Wahr

If and only if ($ \Leftrightarrow $) - - $A \Leftrightarrow B$ ist eine bikonditionale logische Verbindung, die wahr ist, wenn p und q gleich sind, dh beide sind falsch oder beide sind wahr.

Die Wahrheitstabelle lautet wie folgt:

EIN	B.	A ⇔ B.
Wahr	Wahr	Wahr
Wahr	Falsch	Falsch
Falsch	Wahr	Falsch
Falsch	Falsch	Wahr

Tautologien

Eine Tautologie ist eine Formel, die immer für jeden Wert ihrer Satzvariablen gilt.

Example - Beweisen Sie $\lbrack (A \rightarrow B) \land A \rbrack \rightarrow B$ ist eine Tautologie

Die Wahrheitstabelle lautet wie folgt:

EIN	B.	A → B.	(A → B) ∧ A.	[(A → B) ∧ A] → B.
Wahr	Wahr	Wahr	Wahr	Wahr
Wahr	Falsch	Falsch	Falsch	Wahr
Falsch	Wahr	Wahr	Falsch	Wahr
Falsch	Falsch	Wahr	Falsch	Wahr

Wie wir jeden Wert von sehen können $\lbrack (A \rightarrow B) \land A \rbrack \rightarrow B$ ist "wahr", es ist eine Tautologie.

Widersprüche

Ein Widerspruch ist eine Formel, die für jeden Wert ihrer Satzvariablen immer falsch ist.

Example - Beweisen Sie $(A \lor B) \land \lbrack ( \lnot A) \land (\lnot B) \rbrack$ ist ein Widerspruch

Die Wahrheitstabelle lautet wie folgt:

EIN	B.	A ∨ B.	¬ A.	¬ B.	(¬ A) ∧ (¬ B)	(A ∨ B) ∧ [(¬ A) ∧ (¬ B)]
Wahr	Wahr	Wahr	Falsch	Falsch	Falsch	Falsch
Wahr	Falsch	Wahr	Falsch	Wahr	Falsch	Falsch
Falsch	Wahr	Wahr	Wahr	Falsch	Falsch	Falsch
Falsch	Falsch	Falsch	Wahr	Wahr	Wahr	Falsch

Wie wir jeden Wert von sehen können $(A \lor B) \land \lbrack ( \lnot A) \land (\lnot B) \rbrack$ ist "falsch", es ist ein Widerspruch.

Kontingenz

Eine Kontingenz ist eine Formel, die sowohl einige wahre als auch einige falsche Werte für jeden Wert ihrer Satzvariablen enthält.

Example - Beweisen Sie $(A \lor B) \land (\lnot A)$ eine Kontingenz

Die Wahrheitstabelle lautet wie folgt:

EIN	B.	A ∨ B.	¬ A.	(A ∨ B) ∧ (¬ A)
Wahr	Wahr	Wahr	Falsch	Falsch
Wahr	Falsch	Wahr	Falsch	Falsch
Falsch	Wahr	Wahr	Wahr	Wahr
Falsch	Falsch	Falsch	Wahr	Falsch

Wie wir jeden Wert von sehen können $(A \lor B) \land (\lnot A)$ hat sowohl "wahr" als auch "falsch", es ist eine Kontingenz.

Satzäquivalenzen

Zwei Anweisungen X und Y sind logisch äquivalent, wenn eine der folgenden beiden Bedingungen gilt:

• Die Wahrheitstabellen jeder Aussage haben die gleichen Wahrheitswerte.

• Die bi-bedingte Aussage $X \Leftrightarrow Y$ ist eine Tautologie.

Example - Beweisen Sie $\lnot (A \lor B) and \lbrack (\lnot A) \land (\lnot B) \rbrack$ sind gleichwertig

Testen von 1 ^st Methode (Matching Wahrheitstabelle)

EIN	B.	A ∨ B.	¬ (A ∨ B)	¬ A.	¬ B.	[(¬ A) ∧ (¬ B)]
Wahr	Wahr	Wahr	Falsch	Falsch	Falsch	Falsch
Wahr	Falsch	Wahr	Falsch	Falsch	Wahr	Falsch
Falsch	Wahr	Wahr	Falsch	Wahr	Falsch	Falsch
Falsch	Falsch	Falsch	Wahr	Wahr	Wahr	Wahr

Hier können wir die Wahrheitswerte von sehen $\lnot (A \lor B) and \lbrack (\lnot A) \land (\lnot B) \rbrack$ sind gleich, daher sind die Aussagen gleichwertig.

Testen von 2 ^nd Verfahren (Bi-Auflagen)

EIN	B.	¬ (A ∨ B)	[(¬ A) ∧ (¬ B)]	[¬ (A ∨ B)] ⇔ [(¬ A) ∧ (¬ B)]
Wahr	Wahr	Falsch	Falsch	Wahr
Wahr	Falsch	Falsch	Falsch	Wahr
Falsch	Wahr	Falsch	Falsch	Wahr
Falsch	Falsch	Wahr	Wahr	Wahr

Wie $\lbrack \lnot (A \lor B) \rbrack \Leftrightarrow \lbrack (\lnot A ) \land (\lnot B) \rbrack$ ist eine Tautologie, die Aussagen sind gleichwertig.

Invers, Converse und Kontra-positiv

Implikation / wenn-dann $(\rightarrow)$wird auch als bedingte Anweisung bezeichnet. Es besteht aus zwei Teilen -

• Hypothese, p
• Schlussfolgerung, q

Wie bereits erwähnt, wird es als bezeichnet $p \rightarrow q$.

Example of Conditional Statement- "Wenn Sie Ihre Hausaufgaben machen, werden Sie nicht bestraft." Hier ist "du machst deine Hausaufgaben" die Hypothese, p, und "du wirst nicht bestraft" ist die Schlussfolgerung, q.

Inverse- Eine Umkehrung der bedingten Aussage ist die Negation sowohl der Hypothese als auch der Schlussfolgerung. Wenn die Aussage "Wenn p, dann q" lautet, lautet die Umkehrung "Wenn nicht p, dann nicht q". Also die Umkehrung von$p \rightarrow q$ ist $ \lnot p \rightarrow \lnot q$.

Example - Die Umkehrung von "Wenn Sie Ihre Hausaufgaben machen, werden Sie nicht bestraft" ist "Wenn Sie Ihre Hausaufgaben nicht machen, werden Sie bestraft."

Converse- Die Umkehrung der bedingten Aussage wird durch Vertauschen der Hypothese und der Schlussfolgerung berechnet. Wenn die Aussage "Wenn p, dann q" lautet, lautet die Umkehrung "Wenn q, dann p". Das Gegenteil von$p \rightarrow q$ ist $q \rightarrow p$.

Example - Die Umkehrung von "Wenn Sie Ihre Hausaufgaben machen, werden Sie nicht bestraft" ist "Wenn Sie nicht bestraft werden, machen Sie Ihre Hausaufgaben".

Contra-positive- Das Kontra-Positive der Bedingung wird berechnet, indem die Hypothese und die Schlussfolgerung der inversen Aussage ausgetauscht werden. Wenn die Aussage "Wenn p, dann q" lautet, lautet das kontrapositive "Wenn nicht q, dann nicht p". Das kontrapositive von$p \rightarrow q$ ist $\lnot q \rightarrow \lnot p$.

Example - Das Gegenpositive von "Wenn Sie Ihre Hausaufgaben machen, werden Sie nicht bestraft" ist "Wenn Sie bestraft werden, haben Sie Ihre Hausaufgaben nicht gemacht".

Dualitätsprinzip

Das Dualitätsprinzip besagt, dass für jede wahre Aussage auch die doppelte Aussage gilt, die durch Austausch von Gewerkschaften in Schnittpunkte (und umgekehrt) und Austausch von Universalmengen in Nullmengen (und umgekehrt) erhalten wird. Wenn das Doppelte einer Aussage die Aussage selbst ist, wird es gesagtself-dual Erklärung.

Example - Das Dual von $(A \cap B ) \cup C$ ist $(A \cup B) \cap C$

Normalformen

Wir können jeden Satz in zwei normale Formen umwandeln -

• Konjunktiv Normalform
• Disjunktive Normalform

Konjunktiv Normalform

Eine zusammengesetzte Anweisung liegt in konjunktiver Normalform vor, wenn sie durch Operieren von AND zwischen Variablen (Negation der enthaltenen Variablen) erhalten wird, die mit ORs verbunden sind. In Bezug auf Mengenoperationen handelt es sich um eine zusammengesetzte Anweisung, die von Intersection zwischen mit Unions verbundenen Variablen erhalten wird.

Examples

• $(A \lor B) \land (A \lor C) \land (B \lor C \lor D)$

• $(P \cup Q) \cap (Q \cup R)$

Disjunktive Normalform

Eine zusammengesetzte Anweisung liegt in disjunktiver Normalform vor, wenn sie durch Operieren von ODER zwischen Variablen (Negation eingeschlossener Variablen) erhalten wird, die mit UND verbunden sind. In Bezug auf Mengenoperationen handelt es sich um eine zusammengesetzte Aussage, die Union unter Variablen erhält, die mit Schnittpunkten verbunden sind.

Examples

• $(A \land B) \lor (A \land C) \lor (B \land C \land D)$

• $(P \cap Q) \cup (Q \cap R)$

Predicate Logic befasst sich mit Prädikaten, die Sätze sind, die Variablen enthalten.

Prädikatenlogik - Definition

Ein Prädikat ist ein Ausdruck einer oder mehrerer Variablen, die in einer bestimmten Domäne definiert sind. Ein Prädikat mit Variablen kann zu einem Satz gemacht werden, indem entweder der Variablen ein Wert zugewiesen oder die Variable quantifiziert wird.

Das Folgende sind einige Beispiele für Prädikate -

• Es sei E (x, y) "x = y"
• X (a, b, c) bezeichne "a + b + c = 0".
• Es sei M (x, y) "x ist mit y verheiratet"

Gut geformte Formel

Well Formed Formula (wff) ist ein Prädikat, das eines der folgenden Elemente enthält:

• Alle Satzkonstanten und Satzvariablen sind wffs

• Wenn x eine Variable und Y eine wff ist, $\forall x Y$ und $\exists x Y$ sind auch wff

• Wahrheitswert und falsche Werte sind wffs

• Jede Atomformel ist eine wff

• Alle Verbindungen, die wffs verbinden, sind wffs

Quantifizierer

Die Variable der Prädikate wird durch Quantifizierer quantifiziert. In der Prädikatenlogik gibt es zwei Arten von Quantifizierern: Universal Quantifier und Existential Quantifier.

Universal Quantifier

Der universelle Quantifizierer gibt an, dass die Aussagen in seinem Geltungsbereich für jeden Wert der spezifischen Variablen zutreffen. Es ist mit dem Symbol gekennzeichnet$\forall$.

$\forall x P(x)$ wird gelesen, da für jeden Wert von x P (x) wahr ist.

Example - "Der Mensch ist sterblich" kann in die Satzform umgewandelt werden $\forall x P(x)$ wobei P (x) das Prädikat ist, das x bezeichnet, ist sterblich und das Universum des Diskurses sind alle Menschen.

Existenzieller Quantifizierer

Der Existenzquantifizierer gibt an, dass die Anweisungen in seinem Bereich für einige Werte der spezifischen Variablen zutreffen. Es ist mit dem Symbol gekennzeichnet$\exists $.

$\exists x P(x)$ wird gelesen, da für einige Werte von x P (x) wahr ist.

Example - "Manche Menschen sind unehrlich" kann in die Satzform umgewandelt werden $\exists x P(x)$ wobei P (x) das Prädikat ist, das x bezeichnet, unehrlich ist und das Universum des Diskurses einige Menschen sind.

Verschachtelte Quantifizierer

Wenn wir einen Quantifizierer verwenden, der im Rahmen eines anderen Quantifizierers angezeigt wird, wird er als verschachtelter Quantifizierer bezeichnet.

Example

• $\forall\ a\: \exists b\: P (x, y)$ wo $P (a, b)$ bezeichnet $a + b = 0$

• $\forall\ a\: \forall\: b\: \forall\: c\: P (a, b, c)$ wo $P (a, b)$ bezeichnet $a + (b + c) = (a + b) + c$

Note - - $\forall\: a\: \exists b\: P (x, y) \ne \exists a\: \forall b\: P (x, y)$

Um neue Aussagen aus den Aussagen abzuleiten, deren Wahrheit wir bereits kennen, Rules of Inference werden verwendet.

Wofür sind Inferenzregeln?

Mathematische Logik wird häufig für logische Beweise verwendet. Beweise sind gültige Argumente, die die Wahrheitswerte mathematischer Aussagen bestimmen.

Ein Argument ist eine Folge von Anweisungen. Die letzte Aussage ist die Schlussfolgerung und alle vorhergehenden Aussagen werden als Prämissen (oder Hypothese) bezeichnet. Das Symbol "$\therefore$”, (Lesen Sie daher) steht vor dem Abschluss. Ein gültiges Argument ist eines, bei dem die Schlussfolgerung aus den Wahrheitswerten der Prämissen folgt.

Inferenzregeln enthalten die Vorlagen oder Richtlinien zum Erstellen gültiger Argumente aus den bereits vorhandenen Anweisungen.

Tabelle der Inferenzregeln

Inferenzregel	Name	Inferenzregel	Name
$$\begin{matrix} P \\ \hline \therefore P \lor Q \end{matrix}$$	Zusatz	$$\begin{matrix} P \lor Q \\ \lnot P \\ \hline \therefore Q \end{matrix}$$	Disjunktiver Syllogismus
$$\begin{matrix} P \\ Q \\ \hline \therefore P \land Q \end{matrix}$$	Verbindung	$$\begin{matrix} P \rightarrow Q \\ Q \rightarrow R \\ \hline \therefore P \rightarrow R \end{matrix}$$	Hypothetischer Syllogismus
$$\begin{matrix} P \land Q\\ \hline \therefore P \end{matrix}$$	Vereinfachung	$$\begin{matrix} ( P \rightarrow Q ) \land (R \rightarrow S) \\ P \lor R \\ \hline \therefore Q \lor S \end{matrix}$$	Konstruktives Dilemma
$$\begin{matrix} P \rightarrow Q \\ P \\ \hline \therefore Q \end{matrix}$$	Modus Ponens	$$\begin{matrix} (P \rightarrow Q) \land (R \rightarrow S) \\ \lnot Q \lor \lnot S \\ \hline \therefore \lnot P \lor \lnot R \end{matrix}$$	Destruktives Dilemma
$$\begin{matrix} P \rightarrow Q \\ \lnot Q \\ \hline \therefore \lnot P \end{matrix}$$	Modus Tollens

Zusatz

Wenn P eine Prämisse ist, können wir die Additionsregel verwenden, um abzuleiten $ P \lor Q $.

$$\begin{matrix} P \\ \hline \therefore P \lor Q \end{matrix}$$

Beispiel

Sei P der Satz: "Er lernt sehr hart" ist wahr

Deshalb - "Entweder er lernt sehr hart oder er ist ein sehr schlechter Schüler." Hier ist Q der Satz "er ist ein sehr schlechter Schüler".

Verbindung

Wenn P und Q zwei Prämissen sind, können wir die Konjunktionsregel verwenden, um abzuleiten $ P \land Q $.

$$\begin{matrix} P \\ Q \\ \hline \therefore P \land Q \end{matrix}$$

Beispiel

Lassen Sie P - "Er lernt sehr hart"

Lassen Sie Q - "Er ist der beste Junge in der Klasse"

Deshalb - "Er lernt sehr hart und er ist der beste Junge in der Klasse"

Vereinfachung

Wenn $P \land Q$ ist eine Prämisse, wir können die Vereinfachungsregel verwenden, um P abzuleiten.

$$\begin{matrix} P \land Q\\ \hline \therefore P \end{matrix}$$

Beispiel

"Er lernt sehr hart und ist der beste Junge in der Klasse", $P \land Q$

Deshalb - "Er lernt sehr hart"

Modus Ponens

Wenn P und $P \rightarrow Q$ sind zwei Prämissen, können wir Modus Ponens verwenden, um Q abzuleiten.

$$\begin{matrix} P \rightarrow Q \\ P \\ \hline \therefore Q \end{matrix}$$

Beispiel

"Wenn Sie ein Passwort haben, können Sie sich bei Facebook anmelden", $P \rightarrow Q$

"Sie haben ein Passwort", P.

Deshalb - "Sie können sich bei Facebook anmelden"

Modus Tollens

Wenn $P \rightarrow Q$ und $\lnot Q$ Sind zwei Prämissen, können wir Modus Tollens verwenden, um abzuleiten $\lnot P$.

$$\begin{matrix} P \rightarrow Q \\ \lnot Q \\ \hline \therefore \lnot P \end{matrix}$$

Beispiel

"Wenn Sie ein Passwort haben, können Sie sich bei Facebook anmelden", $P \rightarrow Q$

"Sie können sich nicht bei Facebook anmelden", $\lnot Q$

Deshalb - "Sie haben kein Passwort"

Disjunktiver Syllogismus

Wenn $\lnot P$ und $P \lor Q$ sind zwei Prämissen, können wir disjunktiven Syllogismus verwenden, um Q abzuleiten.

$$\begin{matrix} \lnot P \\ P \lor Q \\ \hline \therefore Q \end{matrix}$$

Beispiel

"Das Eis hat keinen Vanillegeschmack", $\lnot P$

"Das Eis hat entweder Vanille- oder Schokoladengeschmack", $P \lor Q$

Deshalb - "Das Eis hat Schokoladengeschmack"

Hypothetischer Syllogismus

Wenn $P \rightarrow Q$ und $Q \rightarrow R$ Sind zwei Prämissen, können wir hypothetischen Syllogismus verwenden, um abzuleiten $P \rightarrow R$

$$\begin{matrix} P \rightarrow Q \\ Q \rightarrow R \\ \hline \therefore P \rightarrow R \end{matrix}$$

Beispiel

"Wenn es regnet, gehe ich nicht zur Schule", $P \rightarrow Q$

"Wenn ich nicht zur Schule gehe, muss ich keine Hausaufgaben machen", $Q \rightarrow R$

Deshalb - "Wenn es regnet, muss ich keine Hausaufgaben machen"

Konstruktives Dilemma

Wenn $( P \rightarrow Q ) \land (R \rightarrow S)$ und $P \lor R$ Sind zwei Prämissen, können wir konstruktives Dilemma ableiten $Q \lor S$.

$$\begin{matrix} ( P \rightarrow Q ) \land (R \rightarrow S) \\ P \lor R \\ \hline \therefore Q \lor S \end{matrix}$$

Beispiel

"Wenn es regnet, werde ich mich verabschieden", $( P \rightarrow Q )$

"Wenn es draußen heiß ist, gehe ich duschen", $(R \rightarrow S)$

"Entweder wird es regnen oder es ist heiß draußen", $P \lor R$

Deshalb - "Ich werde mich verabschieden oder ich werde duschen gehen"

Destruktives Dilemma

Wenn $(P \rightarrow Q) \land (R \rightarrow S)$ und $ \lnot Q \lor \lnot S $ Sind zwei Prämissen, können wir aus dem destruktiven Dilemma ableiten $\lnot P \lor \lnot R$.

$$\begin{matrix} (P \rightarrow Q) \land (R \rightarrow S) \\ \lnot Q \lor \lnot S \\ \hline \therefore \lnot P \lor \lnot R \end{matrix}$$

Beispiel

"Wenn es regnet, werde ich mich verabschieden", $(P \rightarrow Q )$

"Wenn es draußen heiß ist, gehe ich duschen", $(R \rightarrow S)$

"Entweder werde ich mich nicht verabschieden oder ich werde nicht duschen gehen", $\lnot Q \lor \lnot S$

Deshalb - "Entweder regnet es nicht oder es ist draußen nicht heiß"

Die Gruppentheorie ist ein Zweig der Mathematik und der abstrakten Algebra, der eine algebraische Struktur mit dem Namen definiert group. Im Allgemeinen besteht eine Gruppe aus einer Menge von Elementen und einer Operation über zwei beliebige Elemente in dieser Menge, um ein drittes Element auch in dieser Menge zu bilden.

1854 gab der britische Mathematiker Arthur Cayley zum ersten Mal die moderne Definition von Gruppe -

„Eine Reihe von Symbolen, die alle unterschiedlich sind, und so, dass das Produkt von zwei von ihnen (egal in welcher Reihenfolge) oder das Produkt von einem von ihnen in sich selbst zur Gruppe gehört, wird als Gruppe bezeichnet . Diese Symbole sind im Allgemeinen nicht konvertierbar [kommutativ], sondern assoziativ. “

In diesem Kapitel werden wir wissen operators and postulates das bilden die Grundlagen der Mengenlehre, Gruppentheorie und Booleschen Algebra.

Jeder Satz von Elementen in einem mathematischen System kann mit einem Satz von Operatoren und einer Anzahl von Postulaten definiert werden.

EIN binary operatorFür eine Gruppe von Elementen ist eine Regel definiert, die jedem Elementpaar ein eindeutiges Element aus dieser Gruppe zuweist. Zum Beispiel angesichts der Menge$ A = \lbrace 1, 2, 3, 4, 5 \rbrace $, Wir können sagen $\otimes$ ist ein binärer Operator für die Operation $c = a \otimes b$, wenn es eine Regel zum Finden von c für das Paar von angibt $(a,b)$, so dass $a,b,c \in A$.

Das postulateseines mathematischen Systems bilden die Grundannahmen, aus denen Regeln abgeleitet werden können. Die Postulate sind -

Schließung

Eine Menge wird in Bezug auf einen binären Operator geschlossen, wenn der Operator für jedes Elementpaar in der Menge ein eindeutiges Element aus dieser Menge findet.

Beispiel

Lassen $A = \lbrace 0, 1, 2, 3, 4, 5, \dots \rbrace$

Dieser Satz wird unter Binäroperator in geschlossen $(\ast)$, weil für die Operation $c = a \ast b$für jeden $a, b \in A$, das Produkt $c \in A$.

Die Menge wird nicht unter binärer Operator-Teilung geschlossen $(\div)$, weil für die Operation $c = a \div b$für jeden $a, b \in A$befindet sich das Produkt c möglicherweise nicht im Satz A. Wenn $a = 7, b = 2$, dann $c = 3.5$. Hier$a,b \in A$ aber $c \notin A$.

Assoziative Gesetze

Ein binärer Operator $\otimes$ auf einer Menge A ist assoziativ, wenn es die folgende Eigenschaft enthält -

$(x \otimes y) \otimes z = x \otimes (y \otimes z)$, wo $x, y, z \in A $

Beispiel

Lassen $A = \lbrace 1, 2, 3, 4 \rbrace$

Der Betreiber plus $( + )$ ist assoziativ, weil für drei beliebige Elemente, $x,y,z \in A$, die Eigenschaft $(x + y) + z = x + ( y + z )$ hält.

Der Operator minus $( - )$ ist da nicht assoziativ

$$( x - y ) - z \ne x - ( y - z )$$

Kommutative Gesetze

Ein binärer Operator $\otimes$ auf einer Menge A ist kommutativ, wenn es die folgende Eigenschaft enthält -

$x \otimes y = y \otimes x$, wo $x, y \in A$

Beispiel

Lassen $A = \lbrace 1, 2, 3, 4 \rbrace$

Der Betreiber plus $( + )$ ist kommutativ, weil für zwei beliebige Elemente, $x,y \in A$, die Eigenschaft $x + y = y + x$ hält.

Der Operator minus $( - )$ ist da nicht assoziativ

$$x - y \ne y - x$$

Verteilungsgesetze

Zwei binäre Operatoren $\otimes$ und $\circledast$ auf einer Menge A sind über Operator verteilt $\circledast$ wenn die folgende Eigenschaft gilt -

$x \otimes (y \circledast z) = (x \otimes y) \circledast (x \otimes z)$, wo $x, y, z \in A $

Beispiel

Lassen $A = \lbrace 1, 2, 3, 4 \rbrace$

Die Betreiber in $( * )$ und plus $( + )$ sind über Operator + verteilend, weil für drei beliebige Elemente, $x,y,z \in A$, die Eigenschaft $x * ( y + z ) = ( x * y ) + ( x * z )$ hält.

Diese Operatoren sind jedoch nicht verteilend $*$ schon seit

$$x + ( y * z ) \ne ( x + y ) * ( x + z )$$

Identitätselement

Eine Menge A hat ein Identitätselement in Bezug auf eine binäre Operation $\otimes$ auf A, wenn es ein Element gibt $e \in A$, so dass die folgende Eigenschaft gilt -

$e \otimes x = x \otimes e$, wo $x \in A$

Beispiel

Lassen $Z = \lbrace 0, 1, 2, 3, 4, 5, \dots \rbrace$

Das Element 1 ist ein Identitätselement in Bezug auf die Operation $*$ da für jedes Element $x \in Z$,

$$1 * x = x * 1$$

Andererseits gibt es kein Identitätselement für die Operation minus $( - )$

Invers

Wenn eine Menge A ein Identitätselement hat $e$ in Bezug auf einen binären Operator $\otimes $Es wird gesagt, dass es für jedes Element immer eine Umkehrung gibt $x \in A$gibt es ein anderes Element $y \in A$, so dass die folgende Eigenschaft gilt -

$$x \otimes y = e$$

Beispiel

Lassen $A = \lbrace \dots -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, \dots \rbrace$

Angesichts der Operation plus $( + )$ und $e = 0$ist die Umkehrung eines Elements x $(-x)$ schon seit $x + (x) = 0$

De Morgans Gesetz

De Morgans Gesetze geben ein Paar Transformationen zwischen Vereinigung und Schnittmenge von zwei (oder mehr) Mengen in Bezug auf ihre Komplemente. Die Gesetze sind -

$$(A \cup B)' = A' \cap B'$$

$$(A \cap B)' = A' \cup B'$$

Beispiel

Lassen $A = \lbrace 1, 2, 3, 4 \rbrace ,B = \lbrace 1, 3, 5, 7 \rbrace$, und

universelles Set $U = \lbrace 1, 2, 3, \dots, 9, 10 \rbrace$

$A' = \lbrace 5, 6, 7, 8, 9, 10 \rbrace$

$B' = \lbrace 2, 4, 6, 8, 9, 10 \rbrace$

$A \cup B = \lbrace 1, 2, 3, 4, 5, 7 \rbrace$

$A \cap B = \lbrace 1, 3 \rbrace $

$(A \cup B)' = \lbrace 6, 8, 9, 10 \rbrace$

$A' \cap B' = \lbrace 6, 8, 9, 10 \rbrace$

So sehen wir das $(A \cup B)' = A' \cap B'$

$(A \cap B)' = \lbrace 2, 4, 5, 6, 7, 8, 9, 10 \rbrace$

$A' \cup B' = \lbrace 2, 4, 5, 6, 7, 8, 9, 10 \rbrace$

So sehen wir das $(A \cap B)' = A' \cup B'$

Halbgruppe

Eine endliche oder unendliche Menge $‘S’$ mit einer binären Operation $‘\omicron’$ (Zusammensetzung) heißt Halbgruppe, wenn es zwei Bedingungen gleichzeitig erfüllt -

• Closure - Für jedes Paar $(a, b) \in S, \:(a \omicron b)$ muss im Set vorhanden sein $S$.

• Associative - Für jedes Element $a, b, c \in S, (a \omicron b) \omicron c = a \omicron (b \omicron c)$ muss halten.

Beispiel

Die Menge der positiven ganzen Zahlen (ohne Null) mit Additionsoperation ist eine Halbgruppe. Zum Beispiel,$ S = \lbrace 1, 2, 3, \dots \rbrace $

Hier gilt die Schließungseigenschaft wie für jedes Paar $(a, b) \in S, (a + b)$ ist in der Menge S vorhanden. Zum Beispiel $1 + 2 = 3 \in S]$

Assoziative Eigenschaft gilt auch für jedes Element $a, b, c \in S, (a + b) + c = a + (b + c)$. Zum Beispiel,$(1 + 2) + 3 = 1 + (2 + 3) = 5$

Monoid

Ein Monoid ist eine Halbgruppe mit einem Identitätselement. Das Identitätselement (bezeichnet mit$e$ oder E) einer Menge S ist ein solches Element, dass $(a \omicron e) = a$für jedes Element $a \in S$. Ein Identitätselement wird auch als bezeichnetunit element. Ein Monoid hat also drei Eigenschaften gleichzeitig -Closure, Associative, Identity element.

Beispiel

Die Menge der positiven ganzen Zahlen (ohne Null) mit Multiplikationsoperation ist ein Monoid. $S = \lbrace 1, 2, 3, \dots \rbrace $

Hier gilt die Schließungseigenschaft wie für jedes Paar $(a, b) \in S, (a \times b)$ ist in der Menge S vorhanden. [Zum Beispiel $1 \times 2 = 2 \in S$ und so weiter]

Assoziative Eigenschaft gilt auch für jedes Element $a, b, c \in S, (a \times b) \times c = a \times (b \times c)$ [Zum Beispiel, $(1 \times 2) \times 3 = 1 \times (2 \times 3) = 6$ und so weiter]

Die Identitätseigenschaft gilt auch für jedes Element $a \in S, (a \times e) = a$ [Zum Beispiel, $(2 \times 1) = 2, (3 \times 1) = 3$und so weiter]. Hier ist das Identitätselement 1.

Gruppe

Eine Gruppe ist ein Monoid mit einem inversen Element. Das inverse Element (mit I bezeichnet) einer Menge S ist ein solches Element, dass$(a \omicron I) = (I \omicron a) = a$für jedes Element $a \in S$. Eine Gruppe hat also gleichzeitig vier Eigenschaften: i) Abschluss, ii) Assoziativ, iii) Identitätselement, iv) Inverses Element. Die Reihenfolge einer Gruppe G ist die Anzahl der Elemente in G und die Reihenfolge eines Elements in einer Gruppe ist die am wenigsten positive ganze Zahl n, so dass an das Identitätselement dieser Gruppe G ist.

Beispiele

Der Satz von $N \times N$ Nicht-singuläre Matrizen bilden eine Gruppe unter Matrixmultiplikationsoperation.

Das Produkt von zwei $N \times N$ nicht singuläre Matrizen ist auch eine $N \times N$ nicht singuläre Matrix, die die Verschlusseigenschaft enthält.

Die Matrixmultiplikation selbst ist assoziativ. Daher gilt assoziatives Eigentum.

Der Satz von $N \times N$ Nicht-singuläre Matrizen enthalten die Identitätsmatrix, die die Eigenschaft des Identitätselements enthält.

Da alle Matrizen nicht singulär sind, haben sie alle inverse Elemente, die auch nicht singuläre Matrizen sind. Daher gilt auch die inverse Eigenschaft.

Abelsche Gruppe

Eine abelsche Gruppe G ist eine Gruppe, für die das Elementpaar gilt $(a,b) \in G$hält immer kommutatives Recht. Eine Gruppe hat also fünf Eigenschaften gleichzeitig - i) Abschluss, ii) Assoziativ, iii) Identitätselement, iv) Inverses Element, v) Kommutativ.

Beispiel

Die Menge der positiven ganzen Zahlen (einschließlich Null) mit Additionsoperation ist eine abelsche Gruppe. $G = \lbrace 0, 1, 2, 3, \dots \rbrace$

Hier gilt die Schließungseigenschaft wie für jedes Paar $(a, b) \in S, (a + b)$ ist in der Menge S vorhanden. [Zum Beispiel $1 + 2 = 2 \in S$ und so weiter]

Assoziative Eigenschaft gilt auch für jedes Element $a, b, c \in S, (a + b) + c = a + (b + c)$ [Zum Beispiel, $(1 +2) + 3 = 1 + (2 + 3) = 6$ und so weiter]

Die Identitätseigenschaft gilt auch für jedes Element $a \in S, (a \times e) = a$ [Zum Beispiel, $(2 \times 1) = 2, (3 \times 1) = 3$und so weiter]. Hier ist das Identitätselement 1.

Die kommutative Eigenschaft gilt auch für jedes Element $a \in S, (a \times b) = (b \times a)$ [Zum Beispiel, $(2 \times 3) = (3 \times 2) = 3$ und so weiter]

Zyklische Gruppe und Untergruppe

EIN cyclic groupist eine Gruppe, die von einem einzelnen Element generiert werden kann. Jedes Element einer zyklischen Gruppe ist eine Potenz eines bestimmten Elements, das als Generator bezeichnet wird. Eine zyklische Gruppe kann durch einen Generator 'g' erzeugt werden, so dass jedes andere Element der Gruppe als eine Leistung des Generators 'g' geschrieben werden kann.

Beispiel

Die Menge der komplexen Zahlen $\lbrace 1,-1, i, -i \rbrace$ Unter Multiplikationsoperation befindet sich eine zyklische Gruppe.

Es gibt zwei Generatoren - $i$ und $–i$ wie $i^1 = i, i^2 = -1, i^3 = -i, i^4 = 1$ und auch $(–i)^1 = -i, (–i)^2 = -1, (–i)^3 = i, (–i)^4 = 1$welches alle Elemente der Gruppe abdeckt. Daher ist es eine zyklische Gruppe.

Note - A. cyclic groupist immer eine abelsche Gruppe, aber nicht jede abelsche Gruppe ist eine zyklische Gruppe. Die hinzugefügten rationalen Zahlen sind nicht zyklisch, sondern abelsch.

EIN subgroup H ist eine Teilmenge einer Gruppe G (bezeichnet mit $H ≤ G$) wenn es die vier Eigenschaften gleichzeitig erfüllt - Closure, Associative, Identity element, und Inverse.

Eine Untergruppe H einer Gruppe G, die nicht die gesamte Gruppe G umfasst, wird als geeignete Untergruppe bezeichnet (bezeichnet mit $H < G$). Eine Untergruppe einer zyklischen Gruppe ist zyklisch und eine abelsche Untergruppe ist ebenfalls abelisch.

Beispiel

Lass eine Gruppe $G = \lbrace 1, i, -1, -i \rbrace$

Dann sind einige Untergruppen $H_1 = \lbrace 1 \rbrace, H_2 = \lbrace 1,-1 \rbrace$,

Dies ist keine Untergruppe - $H_3 = \lbrace 1, i \rbrace$ weil das $(i)^{-1} = -i$ ist nicht in $H_3$

Teilweise bestelltes Set (POSET)

Eine teilweise geordnete Menge besteht aus einer Menge mit einer binären Beziehung, die reflexiv, antisymmetrisch und transitiv ist. "Teilweise geordneter Satz" wird als POSET abgekürzt.

Beispiele

• Die Menge der reellen Zahlen im Binärbetrieb kleiner oder gleich $(\le)$ ist ein Poset.

  Lass das Set $S = \lbrace 1, 2, 3 \rbrace$ und die Operation ist $\le$

  Die Beziehungen werden sein $\lbrace(1, 1), (2, 2), (3, 3), (1, 2), (1, 3), (2, 3)\rbrace$

  Diese Beziehung R ist reflexiv als $\lbrace (1, 1), (2, 2), (3, 3)\rbrace \in R$

  Diese Beziehung R ist antisymmetrisch, wie

  $\lbrace (1, 2), (1, 3), (2, 3) \rbrace \in R\ and\ \lbrace (1, 2), (1, 3), (2, 3) \rbrace ∉ R$

  Diese Beziehung R ist auch transitiv als $\lbrace (1,2), (2,3), (1,3)\rbrace \in R$.

  Daher ist es ein poset.

• Der Scheitelpunktsatz eines gerichteten azyklischen Graphen unter der Operation 'Erreichbarkeit' ist ein Poset.

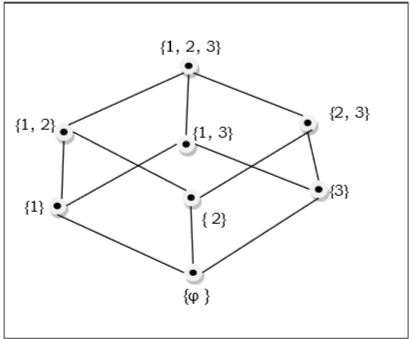
Hasse Diagramm

Das Hasse-Diagramm eines Posets ist der gerichtete Graph, dessen Eckpunkte das Element dieses Posets sind und dessen Bögen die Paare (x, y) im Poset abdecken. Wenn im Poset$x < y$dann erscheint der Punkt x niedriger als der Punkt y im Hasse-Diagramm. Wenn$x<y<z$ Im Poset wird der Pfeil nicht implizit zwischen x und z angezeigt.

Beispiel

Die Menge der Teilmengen von $\lbrace 1, 2, 3 \rbrace = \lbrace \emptyset, \lbrace 1 \rbrace, \lbrace 2 \rbrace, \lbrace 3 \rbrace, \lbrace 1, 2 \rbrace, \lbrace 1, 3 \rbrace, \lbrace 2, 3 \rbrace, \lbrace 1, 2, 3 \rbrace \rbrace$ wird durch das folgende Hasse-Diagramm gezeigt -

Linear geordnetes Set

Eine linear geordnete Menge oder eine insgesamt geordnete Menge ist eine Teilordnungsmenge, in der jedes Elementpaar vergleichbar ist. Die Elemente$a, b \in S$ sollen vergleichbar sein, wenn auch nicht $a \le b$ oder $b \le a$hält. Das Trichotomiegesetz definiert diese geordnete Gesamtmenge. Eine vollständig geordnete Menge kann als Verteilungsgitter mit der Eigenschaft definiert werden$\lbrace a \lor b, a \land b \rbrace = \lbrace a, b \rbrace$ für alle Werte von a und b in Satz S.

Beispiel

Das Powerset von $\lbrace a, b \rbrace$ geordnet nach \ subseteq ist eine vollständig geordnete Menge als alle Elemente der Potenzmenge $P = \lbrace \emptyset, \lbrace a \rbrace, \lbrace b \rbrace, \lbrace a, b\rbrace \rbrace$ sind vergleichbar.

Beispiel für einen nicht vollständigen Auftragssatz

Ein Set $S = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ unter Operation x dividiert y ist keine insgesamt geordnete Menge.

Hier für alle $(x, y) \in S, x | y$müssen halten, aber es ist nicht wahr, dass 2 | 3, da 2 3 nicht teilt oder 3 2 nicht teilt. Daher ist es keine insgesamt geordnete Menge.

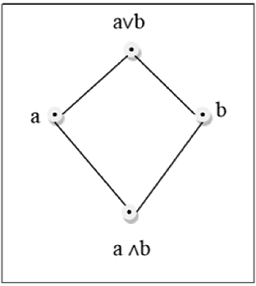
Gitter

Ein Gitter ist ein Poset $(L, \le)$ für die jedes Paar $\lbrace a, b \rbrace \in L$ hat eine kleinste Obergrenze (bezeichnet mit $a \lor b$) und eine größte Untergrenze (bezeichnet mit $a \land b$). LUB$(\lbrace a,b \rbrace)$heißt die Verbindung von a und b. GLB$(\lbrace a,b \rbrace )$ heißt das Treffen von a und b.

Beispiel

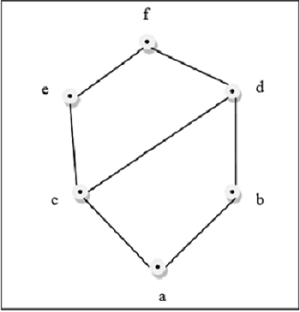
Diese obige Abbildung ist ein Gitter, weil für jedes Paar $\lbrace a, b \rbrace \in L$, ein GLB und ein LUB existieren.

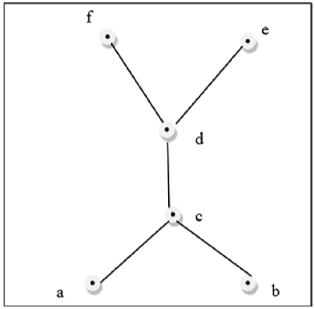
Diese obige Abbildung ist kein Gitter, weil $GLB (a, b)$ und $LUB (e, f)$ ist nicht vorhanden.

Einige andere Gitter werden unten diskutiert -

Begrenztes Gitter

Ein Gitter L wird zu einem begrenzten Gitter, wenn es ein größtes Element 1 und ein kleinstes Element 0 hat.

Ergänztes Gitter

Ein Gitter L wird zu einem komplementierten Gitter, wenn es ein begrenztes Gitter ist und wenn jedes Element im Gitter ein Komplement hat. Ein Element x hat ein Komplement x 'if$\exists x(x \land x’=0 and x \lor x’ = 1)$

Verteilungsgitter

Wenn ein Gitter die folgenden zwei Verteilungseigenschaften erfüllt, wird es als Verteilungsgitter bezeichnet.

• $a \lor (b \land c) = (a \lor b) \land (a \lor c)$

• $a \land (b \lor c) = (a \land b) \lor (a \land c)$

Modulares Gitter

Wenn ein Gitter die folgende Eigenschaft erfüllt, wird es als modulares Gitter bezeichnet.

$a \land( b \lor (a \land d)) = (a \land b) \lor (a \land d)$

Eigenschaften von Gittern

Idempotente Eigenschaften

• $a \lor a = a$

• $a \land a = a$

Absorptionseigenschaften

• $a \lor (a \land b) = a$

• $a \land (a \lor b) = a$

Kommutative Eigenschaften

• $a \lor b = b \lor a$

• $a \land b = b \land a$

Assoziative Eigenschaften

• $a \lor (b \lor c) = (a \lor b) \lor c$

• $a \land (b \land c) = (a \land b) \land c$

Dual eines Gitters

Das Dual eines Gitters wird durch Vertauschen des '$\lor$' und '$\land$'Operationen.

Beispiel

Das Dual von $\lbrack a \lor (b \land c) \rbrack\ is\ \lbrack a \land (b \lor c) \rbrack$

Im täglichen Leben muss man oft die Anzahl aller möglichen Ergebnisse für eine Reihe von Ereignissen herausfinden. Auf wie viele Arten kann beispielsweise eine Jury aus 6 Männern und 4 Frauen aus 50 Männern und 38 Frauen ausgewählt werden? Wie viele verschiedene PAN-Nummern mit 10 Buchstaben können so generiert werden, dass die ersten fünf Buchstaben Großbuchstaben, die nächsten vier Ziffern und der letzte wieder Großbuchstaben sind. Zur Lösung dieser Probleme wird die mathematische Zähltheorie verwendet.Counting umfasst hauptsächlich die grundlegende Zählregel, die Permutationsregel und die Kombinationsregel.

Die Regeln für Summe und Produkt

Das Rule of Sum und Rule of Product werden verwendet, um schwierige Zählprobleme in einfache Probleme zu zerlegen.

• The Rule of Sum - Wenn eine Abfolge von Aufgaben $T_1, T_2, \dots, T_m$ kann in gemacht werden $w_1, w_2, \dots w_m$ Möglichkeiten (die Bedingung ist, dass keine Aufgaben gleichzeitig ausgeführt werden können), dann ist die Anzahl der Möglichkeiten, eine dieser Aufgaben auszuführen $w_1 + w_2 + \dots +w_m$. Wenn wir zwei Aufgaben A und B betrachten, die disjunkt sind (dh$A \cap B = \emptyset$), dann mathematisch $|A \cup B| = |A| + |B|$

• The Rule of Product - Wenn eine Abfolge von Aufgaben $T_1, T_2, \dots, T_m$ kann in gemacht werden $w_1, w_2, \dots w_m$ Wege jeweils und jede Aufgabe kommt nach dem Auftreten der vorherigen Aufgabe an, dann gibt es $w_1 \times w_2 \times \dots \times w_m$Möglichkeiten zur Ausführung der Aufgaben. Mathematisch gesehen, wenn eine Aufgabe B nach einer Aufgabe A eintrifft, dann$|A \times B| = |A|\times|B|$

Beispiel

Question- Ein Junge lebt in X und möchte in Z zur Schule gehen. Von seinem Zuhause X muss er zuerst Y und dann Y nach Z erreichen. Er kann X nach Y entweder mit 3 Buslinien oder 2 Zuglinien fahren. Von dort kann er entweder 4 Buslinien oder 5 Zuglinien wählen, um Z zu erreichen. Wie viele Wege gibt es von X nach Z?

Solution - Von X nach Y kann er hineingehen $3 + 2 = 5$Wege (Regel der Summe). Danach kann er von Y nach Z gehen$4 + 5 = 9$Wege (Regel der Summe). Daher kann er von X bis Z hineingehen$5 \times 9 = 45$ Wege (Produktregel).

Permutationen

EIN permutationist eine Anordnung einiger Elemente, in denen die Reihenfolge wichtig ist. Mit anderen Worten ist eine Permutation eine geordnete Kombination von Elementen.

Beispiele

• Aus einer Menge S = {x, y, z}, indem zwei gleichzeitig genommen werden, sind alle Permutationen -

  $ xy, yx, xz, zx, yz, zy $.

• Wir müssen aus einer Reihe von Zahlen eine Permutation dreistelliger Zahlen bilden $S = \lbrace 1, 2, 3 \rbrace$. Beim Anordnen der Ziffern werden unterschiedliche dreistellige Zahlen gebildet. Die Permutation ist = 123, 132, 213, 231, 312, 321

Anzahl der Permutationen

Die Anzahl der Permutationen von 'n' verschiedenen Dingen, die gleichzeitig 'r' genommen werden, wird mit bezeichnet $n_{P_{r}}$

$$n_{P_{r}} = \frac{n!}{(n - r)!}$$

wo $n! = 1.2.3. \dots (n - 1).n$

Proof - Es gebe 'n' verschiedene Elemente.

Es gibt n Möglichkeiten, den ersten Platz zu füllen. Nach dem Füllen der ersten Stelle (n-1) bleibt die Anzahl der Elemente übrig. Daher gibt es (n-1) Möglichkeiten, den zweiten Platz auszufüllen. Nach dem Ausfüllen des ersten und zweiten Platzes bleibt (n-2) Anzahl der Elemente übrig. Daher gibt es (n-2) Möglichkeiten, den dritten Platz zu belegen. Wir können nun die Anzahl der Möglichkeiten, die r-te Stelle zu füllen, als [n - (r - 1)] = n - r + 1 verallgemeinern

Also, die Gesamtzahl. von Möglichkeiten, vom ersten bis zum r-ten Platz aufzufüllen -

$n_{ P_{ r } } = n (n-1) (n-2)..... (n-r + 1)$

$= [n(n-1)(n-2) ... (n-r + 1)] [(n-r)(n-r-1) \dots 3.2.1] / [(n-r)(n-r-1) \dots 3.2.1]$

Daher,

$n_{ P_{ r } } = n! / (n-r)!$

Einige wichtige Permutationsformeln

• Wenn es n Elemente gibt, von denen$a_1$ sind irgendwie gleich, $a_2$ sind von einer anderen Art gleich; $a_3$ sind gleich der dritten Art und so weiter und $a_r$ sind aus $r^{th}$ Art, wo $(a_1 + a_2 + ... a_r) = n$.

  Dann ist die Anzahl der Permutationen dieser n Objekte = $n! / [(a_1!(a_2!) \dots (a_r!)]$.

• Anzahl der Permutationen von n verschiedenen Elementen, die n Elemente gleichzeitig einnehmen = $n_{P_n} = n!$

• Die Anzahl der Permutationen von n verschiedenen Elementen, die r Elemente gleichzeitig einnehmen, wenn x bestimmte Dinge immer bestimmte Stellen einnehmen = $n-x_{p_{r-x}}$

• Die Anzahl der Permutationen von n verschiedenen Elementen, wenn r bestimmte Dinge immer zusammenkommen, ist - $r! (n−r+1)!$

• Die Anzahl der Permutationen von n verschiedenen Elementen, wenn r bestimmte Dinge niemals zusammenkommen, ist - $n!–[r! (n−r+1)!]$

• Die Anzahl der kreisförmigen Permutationen von n verschiedenen Elementen, die zum Zeitpunkt = x Elemente genommen wurden = $^np_{x}/x$

• Die Anzahl der kreisförmigen Permutationen von n verschiedenen Dingen = $^np_{n}/n$

Einige Probleme

Problem 1 - Wie viele Möglichkeiten haben wir, aus 6 verschiedenen Karten zu permutieren?

Solution - Da wir 6 Karten gleichzeitig aus einem Kartenspiel mit 6 Karten nehmen, ist die Permutation $^6P_{6} = 6! = 720$

Problem 2 - Auf wie viele Arten können die Buchstaben des Wortes "READER" angeordnet werden?

Solution - Das Wort 'READER' enthält 6 Buchstaben (2 E, 1 A, 1D und 2R).

Die Permutation wird sein $= 6! /\: [(2!) (1!)(1!)(2!)] = 180.$

Problem 3 - Wie können die Buchstaben des Wortes 'ORANGE' so angeordnet werden, dass die Konsonanten nur die geraden Positionen einnehmen?

Solution- Das Wort 'ORANGE' enthält 3 Vokale und 3 Konsonanten. Anzahl der Möglichkeiten, die Konsonanten untereinander anzuordnen$= ^3P_{3} = 3! = 6$. Die restlichen 3 freien Plätze werden mit 3 Vokalen gefüllt$^3P_{3} = 3! = 6$Wege. Daher beträgt die Gesamtzahl der Permutationen$6 \times 6 = 36$

Kombinationen

EIN combination ist die Auswahl einiger vorgegebener Elemente, in denen die Reihenfolge keine Rolle spielt.

Die Anzahl aller Kombinationen von n Dingen, die r gleichzeitig genommen werden, ist -

$$^nC_{ { r } } = \frac { n! } { r!(n-r)! }$$

Problem 1

Finden Sie die Anzahl der Teilmengen der Menge $\lbrace1, 2, 3, 4, 5, 6\rbrace$ mit 3 Elementen.

Solution

Die Kardinalität der Menge ist 6 und wir müssen 3 Elemente aus der Menge auswählen. Hier spielt die Bestellung keine Rolle. Daher wird die Anzahl der Teilmengen sein$^6C_{3} = 20$.

Problem 2

Es gibt 6 Männer und 5 Frauen in einem Raum. Auf wie viele Arten können wir 3 Männer und 2 Frauen aus dem Raum auswählen?

Solution

Die Anzahl der Möglichkeiten, 3 Männer aus 6 Männern auszuwählen, ist $^6C_{3}$ und die Anzahl der Möglichkeiten, 2 Frauen aus 5 Frauen auszuwählen, ist $^5C_{2}$

Daher beträgt die Gesamtzahl der Wege - $^6C_{3} \times ^5C_{2} = 20 \times 10 = 200$

Problem 3

Auf wie viele Arten können Sie 3 verschiedene Gruppen von 3 Schülern aus insgesamt 9 Schülern auswählen?

Solution

Nummerieren wir die Gruppen als 1, 2 und 3

Für drei Studenten für 1 Wahl ^st Gruppe, die Anzahl der Möglichkeiten -$^9C_{3}$

Die Anzahl der Möglichkeiten für die Wahl 3 Studenten für 2 ^nd - Gruppe nach dem 1. Gruppe der Wahl -$^6C_{3}$

Die Anzahl der Möglichkeiten für die Wahl 3 Studenten für 3 ^rd Gruppe nach dem 1. Wahl ^st und 2 ^nd Gruppe -$^3C_{3}$

Daher die Gesamtzahl der Wege $= ^9C_{3} \times ^6C_{3} \times ^3C_{3} = 84 \times 20 \times 1 = 1680$

Pascals Identität

Pascal Identität, abgeleitet zuerst von Blasius Pascal in 17 - ^ten Jahrhundert, heißt es, dass die Anzahl der Möglichkeiten k Elemente aus n Elementen zu wählen , ist gleich die Summe der Anzahl von Wegen zu wählen (k-1) Elemente von (n-1) -Elementen und die Anzahl der Möglichkeiten, Elemente aus n-1 Elementen auszuwählen.

Mathematisch für alle positiven ganzen Zahlen k und n: $^nC_{k} = ^n{^-}^1C_{k-1} + ^n{^-}^1{C_k}$

Proof - -

$$^n{^-}^1C_{k-1} + ^n{^-}^1{C_k}$$

$= \frac{ (n-1)! } { (k-1)!(n-k)! } + \frac{ (n-1)! } { k!(n-k-1)! }$

$= (n-1)!(\frac{ k } { k!(n-k)! } + \frac{ n-k } { k!(n-k)! } )$

$= (n-1)! \frac{ n } { k!(n-k)! }$

$= \frac{ n! } { k!(n-k)! }$

$= n_{ C_{ k } }$

Pigeonhole-Prinzip

Der deutsche Mathematiker Peter Gustav Lejeune Dirichlet erklärte 1834 ein Prinzip, das er als Schubladenprinzip bezeichnete. Jetzt ist es als das Pigeonhole-Prinzip bekannt.

Pigeonhole Principlegibt an, dass wenn es weniger Taubenlöcher als die Gesamtzahl der Tauben gibt und jede Taube in ein Taubenloch gelegt wird, mindestens ein Taubenloch mit mehr als einer Taube vorhanden sein muss. Wenn n Tauben in m Schubladen mit n> m gelegt werden, gibt es ein Loch mit mehr als einer Taube.

Beispiele

• Zehn Männer sind in einem Raum und nehmen an Handshakes teil. Wenn jede Person mindestens einmal die Hand schüttelt und niemand mehr als einmal die Hand desselben Mannes schüttelt, nahmen zwei Männer an der gleichen Anzahl von Handshakes teil.

• Es müssen mindestens zwei Personen in einer Klasse von 30 Personen sein, deren Namen mit demselben Alphabet beginnen.

Das Einschluss-Ausschluss-Prinzip

Das Inclusion-exclusion principleberechnet die Kardinalzahl der Vereinigung mehrerer nicht disjunkter Mengen. Für zwei Sätze A und B lautet das Prinzip:

$|A \cup B| = |A| + |B| - |A \cap B|$

Für drei Sätze A, B und C lautet das Prinzip:

$|A \cup B \cup C | = |A| + |B| + |C| - |A \cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C |$

Die verallgemeinerte Formel -

$|\bigcup_{i=1}^{n}A_i|=\sum\limits_{1\leq i<j<k\leq n}|A_i \cap A_j|+\sum\limits_{1\leq i<j<k\leq n}|A_i \cap A_j \cap A_k|- \dots +(-1)^{\pi-1}|A_1 \cap \dots \cap A_2|$

Problem 1

Wie viele ganze Zahlen von 1 bis 50 sind Vielfache von 2 oder 3, aber nicht beide?

Solution

Von 1 bis 100 gibt es $50/2 = 25$ Zahlen, die Vielfache von 2 sind.

Es gibt $50/3 = 16$ Zahlen, die Vielfache von 3 sind.

Es gibt $50/6 = 8$ Zahlen, die Vielfache von 2 und 3 sind.

Damit, $|A|=25$, $|B|=16$ und $|A \cap B|= 8$.

$|A \cup B| = |A| + |B| - |A \cap B| = 25 + 16 - 8 = 33$

Problem 2

In einer Gruppe von 50 Schülern mögen 24 kalte Getränke und 36 heiße Getränke, und jeder Schüler mag mindestens eines der beiden Getränke. Wie viele mögen sowohl Kaffee als auch Tee?

Solution

Sei X die Gruppe von Schülern, die kalte Getränke mögen, und Y die Gruppe von Menschen, die heiße Getränke mögen.

Damit, $| X \cup Y | = 50$, $|X| = 24$, $|Y| = 36$

$|X \cap Y| = |X| + |Y| - |X \cup Y| = 24 + 36 - 50 = 60 - 50 = 10$

Daher gibt es 10 Studenten, die sowohl Tee als auch Kaffee mögen.

Eng verwandt mit den Konzepten des Zählens ist die Wahrscheinlichkeit. Wir versuchen oft, die Ergebnisse von Glücksspielen wie Kartenspielen, Spielautomaten und Lotterien zu erraten. dh wir versuchen die Wahrscheinlichkeit oder Wahrscheinlichkeit zu finden, mit der ein bestimmtes Ergebnis erzielt wird.

Probabilitykann so konzipiert werden, dass die Wahrscheinlichkeit des Auftretens eines Ereignisses ermittelt wird. Mathematisch ist es das Studium zufälliger Prozesse und ihrer Ergebnisse. Die Wahrscheinlichkeitsgesetze haben eine breite Anwendbarkeit in einer Vielzahl von Bereichen wie Genetik, Wettervorhersage, Meinungsumfragen, Aktienmärkte usw.

Grundlegendes Konzept

Die Wahrscheinlichkeitstheorie wurde im 17. Jahrhundert von zwei französischen Mathematikern, Blaise Pascal und Pierre de Fermat, erfunden, die sich mit mathematischen Problemen in Bezug auf den Zufall befassten.

Bevor wir zu den Details der Wahrscheinlichkeit übergehen, wollen wir uns das Konzept einiger Definitionen ansehen.

Random Experiment- Ein Experiment, bei dem alle möglichen Ergebnisse bekannt sind und die genaue Ausgabe nicht im Voraus vorhergesagt werden kann, wird als zufälliges Experiment bezeichnet. Das Werfen einer fairen Münze ist ein Beispiel für ein zufälliges Experiment.

Sample Space- Wenn wir ein Experiment durchführen, wird die Menge S aller möglichen Ergebnisse als Probenraum bezeichnet. Wenn wir eine Münze werfen, wird der Probenraum$S = \left \{ H, T \right \}$

Event- Jede Teilmenge eines Probenraums wird als Ereignis bezeichnet. Nach dem Werfen einer Münze ist es ein Ereignis, den Kopf nach oben zu bringen.

Das Wort "Wahrscheinlichkeit" bedeutet die Wahrscheinlichkeit des Auftretens eines bestimmten Ereignisses. Das Beste, was wir sagen können, ist, wie wahrscheinlich es ist, dass sie eintreten, unter Verwendung der Idee der Wahrscheinlichkeit.

$Probability\:of\:occurence\:of\:an\:event = \frac{Total\:number\:of\:favourable \: outcome}{Total\:number\:of\:Outcomes}$

Da das Auftreten eines Ereignisses zwischen 0% und 100% variiert, variiert die Wahrscheinlichkeit zwischen 0 und 1.

Schritte, um die Wahrscheinlichkeit zu finden

Schritt 1 - Berechnen Sie alle möglichen Ergebnisse des Experiments.

Schritt 2 - Berechnen Sie die Anzahl der günstigen Ergebnisse des Experiments.

Schritt 3 - Wenden Sie die entsprechende Wahrscheinlichkeitsformel an.

Eine Münze werfen

Wenn eine Münze geworfen wird, gibt es zwei mögliche Ergebnisse - Köpfe $(H)$ oder Schwänze $(T)$

Also, Gesamtzahl der Ergebnisse = 2

Daher die Wahrscheinlichkeit, einen Kopf zu bekommen $(H)$ oben ist 1/2 und die Wahrscheinlichkeit, einen Schwanz zu bekommen $(T)$ oben ist 1/2

Würfel werfen

Wenn ein Würfel geworfen wird, können sechs mögliche Ergebnisse oben sein - $1, 2, 3, 4, 5, 6$.

Die Wahrscheinlichkeit einer der Zahlen beträgt 1/6

Die Wahrscheinlichkeit, gerade Zahlen zu erhalten, beträgt 3/6 = 1/2

Die Wahrscheinlichkeit, ungerade Zahlen zu erhalten, beträgt 3/6 = 1/2

Karten von einem Deck nehmen

Wenn aus einem Kartenspiel mit 52 Karten eine Karte ausgewählt wird, ermitteln Sie die Wahrscheinlichkeit, dass ein Ass gezogen wird, und die Wahrscheinlichkeit, dass ein Diamant gezogen wird.

Gesamtzahl möglicher Ergebnisse - 52

Ergebnisse, ein Ass zu sein - 4

Wahrscheinlichkeit, ein Ass zu sein = 4/52 = 1/13

Wahrscheinlichkeit, ein Diamant zu sein = 13/52 = 1/4

Wahrscheinlichkeitsaxiome

• Die Wahrscheinlichkeit eines Ereignisses variiert immer von 0 bis 1. $[0 \leq P(x) \leq 1]$

• Für ein unmögliches Ereignis ist die Wahrscheinlichkeit 0 und für ein bestimmtes Ereignis ist die Wahrscheinlichkeit 1.

• Wenn das Auftreten eines Ereignisses nicht von einem anderen Ereignis beeinflusst wird, werden sie als sich gegenseitig ausschließend oder disjunkt bezeichnet.

  Wenn $A_1, A_2....A_n$ sind also sich gegenseitig ausschließende / disjunkte Ereignisse $P(A_i \cap A_j) = \emptyset $ zum $i \ne j$ und $P(A_1 \cup A_2 \cup.... A_n) = P(A_1) + P(A_2)+..... P(A_n)$

Eigenschaften der Wahrscheinlichkeit

• Wenn es zwei Ereignisse gibt $x$ und $\overline{x}$die komplementär sind, dann ist die Wahrscheinlichkeit des komplementären Ereignisses -

  $$p(\overline{x}) = 1-p(x)$$

• Für zwei nicht disjunkte Ereignisse A und B ist die Wahrscheinlichkeit der Vereinigung zweier Ereignisse -

  $P(A \cup B) = P(A) + P(B)$

• Wenn ein Ereignis A eine Teilmenge eines anderen Ereignisses B ist (dh $A \subset B$), dann ist die Wahrscheinlichkeit von A kleiner oder gleich der Wahrscheinlichkeit von B. $A \subset B$ impliziert $P(A) \leq p(B)$

Bedingte Wahrscheinlichkeit

Die bedingte Wahrscheinlichkeit eines Ereignisses B ist die Wahrscheinlichkeit, dass das Ereignis eintritt, wenn ein Ereignis A bereits eingetreten ist. Dies ist geschrieben als$P(B|A)$.

Mathematisch - $ P(B|A) = P(A \cap B)/ P(A)$

Wenn sich Ereignis A und B gegenseitig ausschließen, ist die bedingte Wahrscheinlichkeit von Ereignis B nach dem Ereignis A die Wahrscheinlichkeit von Ereignis B. $P(B)$.

Problem 1

In einem Land besitzen 50% aller Teenager ein Fahrrad und 30% aller Teenager besitzen ein Fahrrad und Fahrrad. Wie groß ist die Wahrscheinlichkeit, dass ein Teenager ein Fahrrad besitzt, wenn der Teenager ein Fahrrad besitzt?

Solution

Nehmen wir an, A ist das Ereignis von Teenagern, die nur ein Fahrrad besitzen, und B ist das Ereignis von Teenagern, die nur ein Fahrrad besitzen.

Damit, $P(A) = 50/100 = 0.5$ und $P(A \cap B) = 30/100 = 0.3$ von dem gegebenen Problem.

$P(B|A) = P(A \cap B)/ P(A) = 0.3/ 0.5 = 0.6$

Daher beträgt die Wahrscheinlichkeit, dass ein Teenager ein Fahrrad besitzt, wenn der Teenager ein Fahrrad besitzt, 60%.

Problem 2

In einer Klasse spielen 50% aller Schüler Cricket und 25% aller Schüler Cricket und Volleyball. Wie groß ist die Wahrscheinlichkeit, dass ein Schüler Volleyball spielt, wenn der Schüler Cricket spielt?

Solution

Nehmen wir an, A ist das Ereignis von Schülern, die nur Cricket spielen, und B ist das Ereignis von Schülern, die nur Volleyball spielen.

Damit, $P(A) = 50/100 =0.5$ und $P(A \cap B) = 25/ 100 =0.25$ von dem gegebenen Problem.

$P\lgroup B\rvert A \rgroup= P\lgroup A\cap B\rgroup/P\lgroup A \rgroup =0.25/0.5=0.5$

Daher beträgt die Wahrscheinlichkeit, dass ein Schüler Volleyball spielt, wenn der Schüler Cricket spielt, 50%.

Problem 3

Sechs gute Laptops und drei defekte Laptops sind durcheinander. Um die defekten Laptops zu finden, werden alle einzeln nach dem Zufallsprinzip getestet. Wie hoch ist die Wahrscheinlichkeit, dass beide defekten Laptops in den ersten beiden Auswahlmöglichkeiten gefunden werden?

Solution

Sei A das Ereignis, dass wir im ersten Test einen defekten Laptop finden, und B das Ereignis, dass wir im zweiten Test einen defekten Laptop finden.

Daher, $P(A \cap B) = P(A)P(B|A) =3/9 \times 2/8 = 1/12$

Satz von Bayes

Theorem - Wenn A und B zwei sich gegenseitig ausschließende Ereignisse sind, wo $P(A)$ ist die Wahrscheinlichkeit von A und $P(B)$ ist die Wahrscheinlichkeit von B, $P(A | B)$ ist die Wahrscheinlichkeit von A, wenn B wahr ist. $P(B | A)$ ist die Wahrscheinlichkeit von B, wenn A wahr ist, dann heißt es im Bayes-Theorem -

$$P(A|B) = \frac{P(B|A) P(A)}{\sum_{i = 1}^{n}P(B|Ai)P(Ai)}$$

Anwendung des Bayes'schen Theorems

• In Situationen, in denen sich alle Ereignisse des Probenraums gegenseitig ausschließen.

• In Situationen, in denen entweder $P( A_i \cap B )$ für jeden $A_i$ oder $P( A_i )$ und $P(B|A_i)$ für jeden $A_i$ ist bekannt.

Problem

Betrachten Sie drei Stifthalter. Der erste Stifthalter enthält 2 rote und 3 blaue Stifte. der zweite hat 3 rote und 2 blaue Stifte; und der dritte hat 4 rote Stifte und 1 blauen Stift. Es besteht die gleiche Wahrscheinlichkeit, dass jeder Stifthalter ausgewählt wird. Wenn ein Stift zufällig gezeichnet wird, wie hoch ist die Wahrscheinlichkeit, dass es sich um einen roten Stift handelt?

Solution

Lassen $A_i$sei der Fall, dass der i- ^ten Stiftständer ausgewählt ist.

Hier ist i = 1,2,3.

Da die Wahrscheinlichkeit für die Auswahl eines Stifts gleich ist, $P(A_i) = 1/3$

Sei B der Fall, dass ein roter Stift gezeichnet wird.

Die Wahrscheinlichkeit, dass ein roter Stift unter den fünf Stiften des ersten Stiftständers ausgewählt wird,

$P(B|A_1) = 2/5$

Die Wahrscheinlichkeit, dass ein roter Stift unter den fünf Stiften des zweiten Stiftständers ausgewählt wird,

$P(B|A_2) = 3/5$

Die Wahrscheinlichkeit, dass ein roter Stift unter den fünf Stiften des dritten Stiftständers ausgewählt wird,

$P(B|A_3) = 4/5$

Nach dem Satz von Bayes

$P(B) = P(A_1).P(B|A_1) + P(A_2).P(B|A_2) + P(A_3).P(B|A_3)$

$= 1/3 . 2/5\: +\: 1/3 . 3/5\: +\: 1/3 . 4/5$

$= 3/5$

Mathematical inductionist eine Technik zum Nachweis von Ergebnissen oder zur Erstellung von Aussagen für natürliche Zahlen. Dieser Teil veranschaulicht die Methode anhand verschiedener Beispiele.

Definition

Mathematical Induction ist eine mathematische Technik, die verwendet wird, um zu beweisen, dass eine Aussage, eine Formel oder ein Satz für jede natürliche Zahl gilt.

Die Technik umfasst zwei Schritte, um eine Aussage zu beweisen, wie unten angegeben -

Step 1(Base step) - Es zeigt, dass eine Aussage für den Anfangswert wahr ist.

Step 2(Inductive step)- Es beweist, dass, wenn die Aussage für die n- ^te Iteration (oder die Zahl n ) gilt, sie auch für die (n + 1) ^-te Iteration (oder die Zahl n + 1 ) gilt.

Wie es geht

Step 1- Betrachten Sie einen Anfangswert, für den die Aussage wahr ist. Es ist zu zeigen, dass die Aussage für n = Anfangswert wahr ist.

Step 2- Angenommen, die Aussage gilt für jeden Wert von n = k . Dann beweisen Sie, dass die Aussage für n = k + 1 wahr ist . Wir brechen n = k + 1 tatsächlich in zwei Teile, ein Teil ist n = k (was bereits bewiesen ist) und versuchen, den anderen Teil zu beweisen.

Problem 1

$3^n-1$ ist ein Vielfaches von 2 für n = 1, 2, ...

Solution

Step 1 - Für $n = 1, 3^1-1 = 3-1 = 2$ Das ist ein Vielfaches von 2

Step 2 - Nehmen wir an $3^n-1$ ist wahr für $n=k$Daher $3^k -1$ ist wahr (es ist eine Annahme)

Das müssen wir beweisen $3^{k+1}-1$ ist auch ein Vielfaches von 2

$3^{k+1} - 1 = 3 \times 3^k - 1 = (2 \times 3^k) + (3^k - 1)$

Der erste Teil $(2 \times 3k)$ ist sicher ein Vielfaches von 2 und der zweite Teil $(3k -1)$ Dies gilt auch als unsere vorherige Annahme.

Daher, $3^{k+1} – 1$ ist ein Vielfaches von 2.

Es ist also bewiesen, dass $3^n – 1$ ist ein Vielfaches von 2.

Problem 2

$1 + 3 + 5 + ... + (2n-1) = n^2$ zum $n = 1, 2, \dots $

Solution

Step 1 - Für $n=1, 1 = 1^2$Somit ist Schritt 1 erfüllt.

Step 2 - Nehmen wir an, die Aussage gilt für $n=k$.

Daher, $1 + 3 + 5 + \dots + (2k-1) = k^2$ ist wahr (es ist eine Annahme)

Das müssen wir beweisen $1 + 3 + 5 + ... + (2(k+1)-1) = (k+1)^2$ gilt auch

$1 + 3 + 5 + \dots + (2(k+1) - 1)$

$= 1 + 3 + 5 + \dots + (2k+2 - 1)$

$= 1 + 3 + 5 + \dots + (2k + 1)$

$= 1 + 3 + 5 + \dots + (2k - 1) + (2k + 1)$

$= k^2 + (2k + 1)$

$= (k + 1)^2$

Damit, $1 + 3 + 5 + \dots + (2(k+1) - 1) = (k+1)^2$ halten, was den Schritt 2 erfüllt.

Daher, $1 + 3 + 5 + \dots + (2n - 1) = n^2$ ist bewiesen.

Problem 3

Beweise das $(ab)^n = a^nb^n$ gilt für jede natürliche Zahl $n$

Solution

Step 1 - Für $n=1, (ab)^1 = a^1b^1 = ab$Somit ist Schritt 1 erfüllt.

Step 2 - Nehmen wir an, die Aussage gilt für $n=k$Daher $(ab)^k = a^kb^k$ ist wahr (es ist eine Annahme).

Das müssen wir beweisen $(ab)^{k+1} = a^{k+1}b^{k+1}$ auch halten

Gegeben, $(ab)^k = a^k b^k$

Oder, $(ab)^k (ab) = (a^k b^k ) (ab)$ [Beide Seiten mit 'ab' multiplizieren]

Oder, $(ab)^{k+1} = (aa^k) ( bb^k)$

Oder, $(ab)^{k+1} = (a^{k+1}b^{k+1})$

Somit ist Schritt 2 bewiesen.

Damit, $(ab)^n = a^nb^n$ gilt für jede natürliche Zahl n.

Starke Induktion

Starke Induktion ist eine andere Form der mathematischen Induktion. Durch diese Induktionstechnik können wir beweisen, dass eine Satzfunktion,$P(n)$ gilt für alle positiven ganzen Zahlen, $n$mit den folgenden Schritten -

• Step 1(Base step) - Es beweist, dass der ursprüngliche Satz $P(1)$ wahr.

• Step 2(Inductive step) - Es beweist, dass die bedingte Aussage $[P(1) \land P(2) \land P(3) \land \dots \land P(k)] → P(k + 1)$ gilt für positive ganze Zahlen $k$.

In diesem Kapitel werden wir diskutieren, wie rekursive Techniken Sequenzen ableiten und zur Lösung von Zählproblemen verwendet werden können. Die Prozedur zum rekursiven Finden der Terme einer Sequenz wird aufgerufenrecurrence relation. Wir untersuchen die Theorie der linearen Wiederholungsrelationen und ihre Lösungen. Schließlich führen wir Generierungsfunktionen zum Lösen von Wiederholungsrelationen ein.

Definition

Eine Wiederholungsrelation ist eine Gleichung, die rekursiv eine Sequenz definiert, bei der der nächste Term eine Funktion der vorherigen Terme ist (Ausdrücken) $F_n$ als eine Kombination von $F_i$ mit $i < n$).

Example - Fibonacci-Serie - $F_n = F_{n-1} + F_{n-2}$, Turm von Hanoi - $F_n = 2F_{n-1} + 1$

Lineare Wiederholungsbeziehungen

Eine lineare Wiederholungsgleichung vom Grad k oder der Ordnung k ist eine Wiederholungsgleichung im Format $x_n= A_1 x_{n-1}+ A_2 x_{n-1}+ A_3 x_{n-1}+ \dots A_k x_{n-k} $($A_n$ ist eine Konstante und $A_k \neq 0$) auf einer Folge von Zahlen als Polynom ersten Grades.

Dies sind einige Beispiele für lineare Wiederholungsgleichungen -

Wiederholungsbeziehungen	Anfangswerte	Lösungen
F n = F n-1 + F n-2	a 1 = a 2 = 1	Fibonacci-Nummer
F n = F n-1 + F n-2	a 1 = 1, a 2 = 3	Lucas Nummer
F n = F n-2 + F n-3	a 1 = a 2 = a 3 = 1	Padovan-Sequenz
F n = 2F n-1 + F n-2	a 1 = 0, a 2 = 1	Pell Nummer

So lösen Sie die lineare Wiederholungsbeziehung

Angenommen, eine lineare geordnete Wiederholungsbeziehung mit zwei Ordnungen ist - $F_n = AF_{n-1} +BF_{n-2}$ wobei A und B reelle Zahlen sind.

Die charakteristische Gleichung für die obige Wiederholungsrelation lautet -

$$x^2 - Ax - B = 0$$

Beim Auffinden der Wurzeln können drei Fälle auftreten -

Case 1 - Wenn diese Gleichung wie folgt lautet $(x- x_1)(x- x_1) = 0$ und es produziert zwei verschiedene echte Wurzeln $x_1$ und $x_2$, dann $F_n = ax_1^n+ bx_2^n$ist die Lösung. [Hier sind a und b Konstanten]

Case 2 - Wenn diese Gleichung wie folgt lautet $(x- x_1)^2 = 0$ und es produziert eine einzige echte Wurzel $x_1$, dann $F_n = a x_1^n+ bn x_1^n$ ist die Lösung.

Case 3 - Wenn die Gleichung zwei unterschiedliche komplexe Wurzeln erzeugt, $x_1$ und $x_2$ in polarer Form $x_1 = r \angle \theta$ und $x_2 = r \angle(- \theta)$, dann $F_n = r^n (a cos(n\theta)+ b sin(n\theta))$ ist die Lösung.

Problem 1

Lösen Sie die Wiederholungsrelation $F_n = 5F_{n-1} - 6F_{n-2}$ wo $F_0 = 1$ und $F_1 = 4$

Solution

Die charakteristische Gleichung der Wiederholungsrelation lautet -

$$x^2 - 5x + 6 = 0,$$

Damit, $(x - 3) (x - 2) = 0$

Daher sind die Wurzeln -

$x_1 = 3$ und $x_2 = 2$

Die Wurzeln sind real und verschieden. Dies ist also in Form von Fall 1

Daher ist die Lösung -

$$F_n = ax_1^n + bx_2^n$$

Hier, $F_n = a3^n + b2^n\ (As\ x_1 = 3\ and\ x_2 = 2)$

Deshalb,

$1 = F_0 = a3^0 + b2^0 = a+b$

$4 = F_1 = a3^1 + b2^1 = 3a+2b$

Wenn wir diese beiden Gleichungen lösen, erhalten wir $ a = 2$ und $b = -1$

Daher ist die endgültige Lösung -

$$F_n = 2.3^n + (-1) . 2^n = 2.3^n - 2^n $$

Problem 2

Lösen Sie die Wiederholungsrelation - $F_n = 10F_{n-1} - 25F_{n-2}$ wo $F_0 = 3$ und $F_1 = 17$

Solution

Die charakteristische Gleichung der Wiederholungsrelation lautet -

$$ x^2 - 10x -25 = 0$$

Damit $(x - 5)^2 = 0$

Daher gibt es eine einzige echte Wurzel $x_1 = 5$

Da es eine einzelne Wurzel mit echtem Wert gibt, liegt dies in Form von Fall 2 vor

Daher ist die Lösung -

$F_n = ax_1^n + bnx_1^n$

$3 = F_0 = a.5^0 +(b)(0.5)^0 = a$

$17 = F_1 = a.5^1 + b.1.5^1 = 5a+5b$

Wenn wir diese beiden Gleichungen lösen, erhalten wir $a = 3$ und $b = 2/5$

Daher ist die endgültige Lösung - $F_n = 3.5^n +( 2/5) .n.2^n $

Problem 3

Lösen Sie die Wiederholungsrelation $F_n = 2F_{n-1} - 2F_{n-2}$ wo $F_0 = 1$ und $F_1 = 3$

Solution

Die charakteristische Gleichung der Wiederholungsrelation lautet -

$$x^2 -2x -2 = 0$$

Daher sind die Wurzeln -

$x_1 = 1 + i$ und $x_2 = 1 - i$

In polarer Form

$x_1 = r \angle \theta$ und $x_2 = r \angle(- \theta),$ wo $r = \sqrt 2$ und $\theta = \frac{\pi}{4}$

Die Wurzeln sind imaginär. Dies ist also in Form von Fall 3.

Daher ist die Lösung -

$F_n = (\sqrt 2 )^n (a cos(n .\sqcap /4) + b sin(n .\sqcap /4))$

$1 = F_0 = (\sqrt 2 )^0 (a cos(0 .\sqcap /4) + b sin(0 .\sqcap /4) ) = a$

$3 = F_1 = (\sqrt 2 )^1 (a cos(1 .\sqcap /4) + b sin(1 . \sqcap /4) ) = \sqrt 2 ( a/ \sqrt 2 + b/ \sqrt 2)$

Wenn wir diese beiden Gleichungen lösen, erhalten wir $a = 1$ und $b = 2$

Daher ist die endgültige Lösung -

$F_n = (\sqrt 2 )^n (cos(n .\pi /4 ) + 2 sin(n .\pi /4 ))$

Inhomogene Wiederholungsbeziehung und bestimmte Lösungen

Eine Wiederholungsbeziehung wird als inhomogen bezeichnet, wenn sie in der Form vorliegt

$F_n = AF_{n-1} + BF_{n-2} + f(n)$ wo $f(n) \ne 0$

Die damit verbundene homogene Wiederholungsbeziehung ist $F_n = AF_{n–1} + BF_{n-2}$

Die Lösung $(a_n)$ einer inhomogenen Wiederholungsbeziehung besteht aus zwei Teilen.

Der erste Teil ist die Lösung $(a_h)$ der zugehörigen homogenen Wiederholungsrelation und des zweiten Teils ist die besondere Lösung $(a_t)$.

$$a_n=a_h+a_t$$

Die Lösung des ersten Teils erfolgt mithilfe der im vorherigen Abschnitt beschriebenen Verfahren.

Um die jeweilige Lösung zu finden, finden wir eine geeignete Testlösung.

Lassen $f(n) = cx^n$;; Lassen$x^2 = Ax + B$ sei die charakteristische Gleichung der zugehörigen homogenen Wiederholungsrelation und lass $x_1$ und $x_2$ sei seine Wurzeln.

• Wenn $x \ne x_1$ und $x \ne x_2$, dann $a_t = Ax^n$

• Wenn $x = x_1$, $x \ne x_2$, dann $a_t = Anx^n$

• Wenn $x = x_1 = x_2$, dann $a_t = An^2x^n$

Beispiel

Sei eine inhomogene Wiederholungsrelation $F_n = AF_{n–1} + BF_{n-2} + f(n)$ mit charakteristischen Wurzeln $x_1 = 2$ und $x_2 = 5$. Versuchslösungen für verschiedene mögliche Werte von$f(n)$ sind wie folgt -