Modellierung der Division einer ganzen Zahl durch einen Bruch
In dieser Lektion lernen wir, wie Sie mithilfe des Flächenmodells eine ganze Zahl durch einen Bruch teilen. Es gibt eine ganze Zahl und einen Bruch, der diese ganze Zahl teilt. Wir betrachten eine ganze Zahl als so viele Quadrate, wie die Zahl angibt. Wir teilen jedes der Quadrate in so viele Teile, wie der Nenner des Bruchs angibt. Wir finden das Ergebnis dieser Division, indem wir die Gesamtzahl der Teile der Quadrate zählen.
Example:
Teilen Sie 3 ÷ $ \ frac {1} {2} $ mit einem Flächenmodell.
Solution
Step 1:
Die ganze Zahl 3 wird als drei Quadrate genommen. Da der Bruchteil die Hälfte beträgt, wird jedes der Quadrate in zwei Hälften geteilt.
Step 2:
Jetzt werden die Hälften in allen drei Quadraten gezählt und als 6 ermittelt. Dies ist die Antwort, die wir erhalten, wenn wir 3 durch $ \ frac {1} {2} $ teilen .
Also 3 ÷ $ \ frac {1} {2} $ = 6
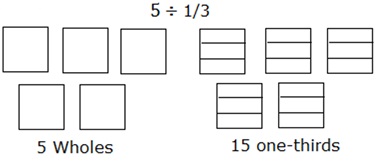
Teilen Sie 5 ÷ $ \ frac {1} {3} $ mit einem Flächenmodell.
Lösung
Step 1:
Die Aufteilung von 5 in ein Drittel kann wie folgt modelliert werden:
Betrachten Sie 5 Quadrate als 5 Ganzheiten. Jedes der Quadrate ist weiter in drei Teile oder ein Drittel unterteilt.
Step 2:
Wenn Sie dann die Gesamtzahl solcher Teile der Quadrate oder Ganzes zählen, erhalten Sie eine Antwort von 15.
Also, 5 ÷ $ \ frac {1} {3} $ = 15
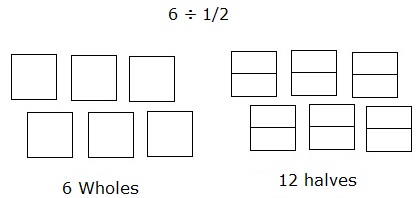
Teilen Sie 6 ÷ $ \ frac {1} {2} $ mit einem Flächenmodell.
Lösung
Step 1:
Das Teilen von 6 in eine Hälfte kann wie folgt modelliert werden:
Betrachten Sie 6 Quadrate als 6 Ganzheiten. Jedes der Quadrate ist weiter in zwei Teile oder eine Hälfte unterteilt.
Step 2:
Wenn Sie dann die Gesamtzahl solcher Teile der Quadrate oder Ganzes zählen, erhalten Sie die Antwort 12.
Also 6 ÷ $ \ frac {1} {2} $ = 12