Modellierung der Multiplikation geeigneter Brüche
Verwenden wir ein Flächenmodell, um Brüche zu multiplizieren. Das Flächenmodell gibt uns ein gutes Bild davon, was passiert, wenn wir zwei Brüche multiplizieren. Wir sehen das Problem in zwei Dimensionen. Wir repräsentieren die Höhe mit einem Bruch und die Breite mit einem anderen Bruch. Es ist wichtig, diese Art von Zusammenhängen in der Mathematik zu sehen.
Multiplizieren Sie die Brüche mit einem Flächenmodell $ \ frac {1} {3} $ × $ \ frac {1} {3} $
Lösung
Step 1:
In diesem Problem möchten wir $ \ frac {1} {3} $ von $ \ frac {1} {3} $ finden
Step 2:
Zuerst teilen wir die Höhe eines Rechtecks in 3 gleiche Teile.

Step 3:
Wir schattieren einen Teil, um $ \ frac {1} {3} $ darzustellen

Step 4:
Als nächstes teilen wir die Breite in 3 gleiche Teile und schattieren 1 Teil, um es zu $ \ frac {1} {3} $ zu machen
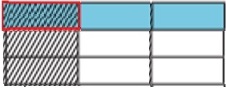
Step 5:
Jetzt können wir das Produkt herausfinden. Der Teil, an dem sich die Schattierung überlappt, repräsentiert den Zähler. Die Gesamtzahl der Teile repräsentiert den Nenner. Es gibt insgesamt 9 Teile und 1 Teil überlappt sich.
Step 6:
Das Produkt ist also $ \ frac {1} {9} $ .
$ \ frac {1} {3} $ × $ \ frac {1} {3} $ = $ \ frac {1} {9} $
Multiplizieren Sie die Brüche mit einem Flächenmodell $ \ frac {2} {3} $ × $ \ frac {1} {3} $
Lösung
Step 1:
In diesem Problem möchten wir $ \ frac {2} {3} $ von $ \ frac {1} {3} $ finden
Step 2:
Zuerst teilen wir die Höhe eines Rechtecks in 3 gleiche Teile.

Step 3:
Wir schattieren einen Teil, um $ \ frac {1} {3} $ darzustellen

Step 4:
Als nächstes teilen wir die Breite in 3 gleiche Teile und schattieren 2 Teile, um sie zu $ \ frac {2} {3} $ zu machen
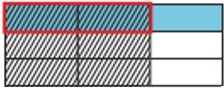
Step 5:
Jetzt können wir das Produkt herausfinden. Der Teil, an dem sich die Schattierung überlappt, repräsentiert den Zähler. Die Gesamtzahl der Teile repräsentiert den Nenner. Es gibt insgesamt 9 Teile und 2 der Teile überlappen sich.
Step 6:
Das Produkt ist also $ \ frac {2} {9} $ .
$ \ frac {2} {3} $ × $ \ frac {1} {3} $ = $ \ frac {2} {9} $
Multiplizieren Sie die Brüche mit einem Flächenmodell $ \ frac {1} {2} $ × $ \ frac {1} {3} $
Lösung
Step 1:
In diesem Problem möchten wir $ \ frac {1} {2} $ von $ \ frac {1} {3} $ finden
Step 2:
Zuerst teilen wir die Höhe eines Rechtecks in 3 gleiche Teile.

Step 3:
Wir schattieren einen Teil, um $ \ frac {1} {3} $ darzustellen

Step 4:
Als nächstes teilen wir die Breite in 2 gleiche Teile und schattieren 1 Teil, um es zu $ \ frac {1} {2} $ zu machen
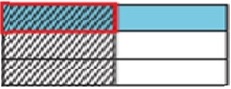
Step 5:
Jetzt können wir das Produkt herausfinden. Der Teil, an dem sich die Schattierung überlappt, repräsentiert den Zähler. Die Gesamtzahl der Teile repräsentiert den Nenner. Es gibt insgesamt 6 Teile und 1 Teil überlappt sich.
Step 6:
Das Produkt ist also $ \ frac {1} {6} $ .
$ \ frac {1} {2} $ × $ \ frac {1} {3} $ = $ \ frac {1} {6} $