Akuntansi Biaya - Analisis CVP

Analisis Biaya-Volume-Keuntungan (CVP) juga dikenal sebagai Analisis Break-Even. Setiap organisasi bisnis bekerja untuk memaksimalkan keuntungannya. Dengan bantuan analisis CVP, manajemen mempelajari hubungan keuntungan dan tingkat produksi.

Analisis CVP berkaitan dengan tingkat aktivitas di mana total penjualan sama dengan total biaya dan ini disebut sebagai titik impas. Dengan kata lain, kami mempelajari nilai penjualan, biaya dan keuntungan pada berbagai tingkat produksi. Analisis CVP menyoroti hubungan antara biaya, nilai penjualan, dan laba.

Asumsi

Mari kita lihat asumsi untuk analisis CVP:

Biaya variabel tetap variabel dan biaya tetap tetap statis di setiap tingkat produksi.
Volume penjualan tidak mempengaruhi harga jual produk. Kita dapat mengasumsikan harga jual konstan.
Di semua tingkat penjualan, volume, material, dan biaya tenaga kerja tetap konstan.
Efisiensi dan produktivitas tetap tidak berubah di semua tingkat volume penjualan.
Bauran penjualan di semua tingkat penjualan tetap konstan dalam situasi multi-produk.
Faktor relevan yang mempengaruhi biaya dan pendapatan hanya volume.
Volume penjualan sama dengan volume produksi.

Persamaan Biaya Marjinal

Persamaan untuk elemen biaya adalah sebagai berikut:

Sales = Variable costs + Fixed Expenses ± Profit /Loss

                     Or
                     
Sales – Variable Cost = Fixed Expenses ± Profit /Loss

                     Or
                     
Sales – Variable Cost = Contribution

Empat konsep berikut ini, perhitungannya, dan aplikasinya perlu dipahami untuk mengetahui hubungan matematis antara biaya, volume, dan keuntungan:

Contribution
Rasio Volume Laba (Rasio P / V atau Kontribusi / Penjualan (C / S))
Break-Even Point
Margin of Safety

Kontribusi

Contribution = Sales – Marginal Cost

Kontribusi dalam topik Marginal Costing telah kita bahas di atas.

Rasio Volume-Laba

Rasio Laba / Volume (P / V) dihitung sambil mempelajari profitabilitas operasi bisnis dan untuk membangun hubungan antara Penjualan dan Kontribusi. Ini adalah salah satu rasio terpenting, dihitung sebagai berikut:

Rasio ^P ⁄ _V =

Kontribusi / Penjualan

Biaya Tetap + Laba / Penjualan

Penjualan - Biaya Variabel / Penjualan

Perubahan keuntungan Kontribusi / Perubahan Penjualan

Rasio P / V berbagi hubungan langsung dengan keuntungan. Semakin tinggi rasio P / V, semakin banyak keuntungan dan sebaliknya.

Break-Even Point

Ketika total biaya menjalankan bisnis sama dengan total penjualan, itu disebut titik impas. Kontribusi sama dengan biaya tetap pada saat ini. Berikut rumus untuk menghitung break-even point:

BEP (dalam satuan) =

Total Biaya Tetap / Harga Jual per Unit - Biaya Marjinal per Unit

Total Biaya Tetap / Kontribusi per Unit

Titik impas berdasarkan total penjualan:

Tetap Biaya / ^P / _V Ratio

Perhitungan output atau nilai penjualan di mana keuntungan yang diinginkan diperoleh:

Biaya Tetap + Keuntungan / Harga Jual yang Diinginkan per Unit - Biaya Marjinal per Unit

Biaya Tetap + Keuntungan / Kontribusi yang Diinginkan per Unit

Titik Impas Komposit

Suatu perusahaan mungkin memiliki unit produksi yang berbeda, di mana mereka dapat menghasilkan produk yang sama. Dalam hal ini, gabungan biaya tetap dari setiap unit produksi dan total penjualan gabungan dipertimbangkan untuk mengetahui BEP.

Constant Product - Pendekatan Campuran Dalam pendekatan ini, rasio adalah konstan untuk produk dari semua unit produksi.
Variable Product - Pendekatan Campuran Dalam pendekatan ini, preferensi produk didasarkan pada rasio yang lebih besar.

Margin of Safety

Kelebihan penjualan di BEP dikenal sebagai margin of safety. Karena itu,

Margin of safety = Actual Sales − Sales at BEP

Margin keselamatan dapat dihitung dengan bantuan rumus berikut:

Margin of Safety =

Rasio Laba / ^P ⁄ _V.

Keuntungan / Kontribusi per Unit

Bagan Impas

Break-Even Chart adalah representasi grafis yang paling berguna dari biaya marjinal. Ini mengubah data akuntansi menjadi laporan yang dapat dibaca berguna. Taksiran keuntungan, kerugian, dan biaya dapat ditentukan pada berbagai tingkat produksi. Mari kita ambil contoh.

Contoh

Hitung titik impas dan gambar grafik titik impas dari data berikut:

Fixed Cost    = Rs 2,50,000
Variable Cost = Rs 15 per unit
Selling Price = Rs 25 per unit
Production level in units 12,000, 15,000, 20,000, 25,000, 30,000, and 40,000.

Solution:

BEP =

Biaya Tetap / Kontribusi per unit

Rs 2.50.000 / Rs 10 × (Rs 25 - Rs 15)

= 25.000 unit

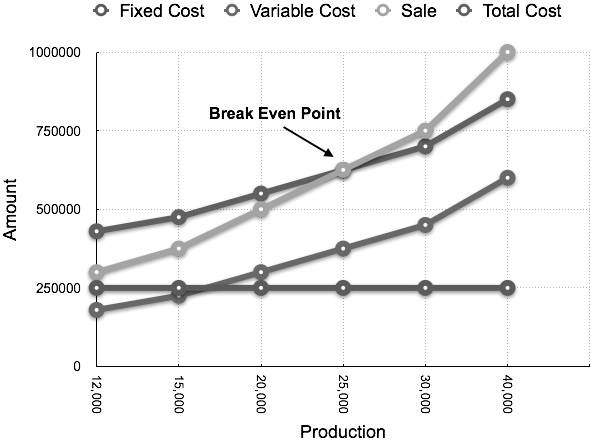
Pada tingkat produksi 25.000 unit, total biaya menjadi Rs 6,25.000.

(Dihitung sebagai (25000 × 14) + 2.50000)

Pernyataan yang menunjukkan Profit & Margin of safety pada berbagai tingkat produksi Break Even Sale = Rs 6,25,000 (25,000 x 25)
Produksi (Dalam Unit)	Penjualan Total (Dalam Rs)	Total biaya (Dalam Rs)	Keuntungan (Penjualan - Biaya) (Dalam Rs)	Margin keamanan (Keuntungan / Kontribusi per unit) (Dalam Unit)
12000	3,00,000	4,30,000	-1,30,000
15000	3,75,000	4,75,000	-1,00,000
20000	5,00,000	5,50,000	-50,000
25000	6,25,000	6,25,000	(BEP)	(BEP)
30000	7,50,000	7,00,000	50.000	5.000
40000	10,00,000	8,50,000	1,50,000	15.000

Bagan terkait yang diplot sebagai produksi terhadap jumlah muncul sebagai berikut: