Komunikasi Analog - Panduan Cepat

Kata komunikasi muncul dari kata Latin commūnicāre, yang berarti “berbagi”. Komunikasi adalah langkah dasar untuk pertukaran informasi.

Misalnya, bayi dalam buaian, berkomunikasi dengan tangisan ketika dia membutuhkan ibunya. Seekor sapi meraung keras saat berada dalam bahaya. Seseorang berkomunikasi dengan bantuan bahasa. Komunikasi adalah jembatan untuk berbagi.

Communication dapat didefinisikan sebagai proses pertukaran informasi melalui sarana seperti kata-kata, tindakan, tanda, dll., antara dua atau lebih individu.

Bagian dari Sistem Komunikasi

Setiap sistem yang menyediakan komunikasi terdiri dari tiga bagian penting dan dasar seperti yang ditunjukkan pada gambar berikut.

• Senderadalah orang yang mengirim pesan. Ini bisa menjadi stasiun pemancar dari mana sinyal ditransmisikan.

• Channel adalah media yang digunakan sinyal pesan untuk mencapai tujuan.

• Receiveradalah orang yang menerima pesan tersebut. Ini bisa menjadi stasiun penerima di mana sinyal yang dikirim sedang diterima.

Jenis Sinyal

Menyampaikan suatu informasi dengan beberapa cara seperti gerak tubuh, suara, tindakan, dll, dapat disebut sebagai signaling. Oleh karena itu, sinyal dapat menjadi sumber energi yang mengirimkan beberapa informasi. Sinyal ini membantu membangun komunikasi antara pengirim dan penerima.

Sebuah impuls listrik atau gelombang elektromagnetik yang menempuh jarak untuk menyampaikan pesan, dapat disebut sebagai a signal dalam sistem komunikasi.

Tergantung pada karakteristiknya, sinyal diklasifikasikan menjadi dua jenis: Analog dan Digital. Sinyal Analog dan Digital selanjutnya diklasifikasikan, seperti yang ditunjukkan pada gambar berikut.

Sinyal analog

Sinyal variasi waktu kontinu, yang merepresentasikan jumlah waktu yang bervariasi dapat disebut sebagai Analog Signal. Sinyal ini terus berubah terhadap waktu, sesuai dengan nilai sesaat dari kuantitas, yang mewakilinya.

Contoh

Mari kita pertimbangkan keran yang mengisi tangki dengan kapasitas 100 liter dalam satu jam (6 pagi hingga 7 pagi). Porsi pengisian tangki bervariasi menurut waktu yang berbeda-beda. Artinya, setelah 15 menit (6:15 pagi) seperempat bagian tangki terisi, sedangkan pada pukul 06.45, 3/4 tangki terisi.

Jika kita mencoba untuk memplot variasi bagian air dalam tangki menurut waktu yang berbeda, akan terlihat seperti gambar berikut.

Karena hasil yang ditunjukkan pada gambar ini bervariasi (meningkat) menurut waktu, ini time varying quantitydapat dipahami sebagai kuantitas Analog. Sinyal yang mewakili kondisi ini dengan garis miring pada gambar, adalahAnalog Signal. Komunikasi berdasarkan sinyal analog dan nilai analog disebut sebagaiAnalog Communication.

Sinyal Digital

Suatu sinyal yang bersifat diskrit atau yang bentuknya tidak kontinu dapat disebut sebagai a Digital signal. Sinyal ini memiliki nilai individual, dilambangkan secara terpisah, yang tidak didasarkan pada nilai sebelumnya, seolah-olah diturunkan pada saat tertentu itu.

Contoh

Mari kita pertimbangkan sebuah kelas yang memiliki 20 siswa. Jika kehadiran mereka dalam seminggu diplot, maka akan terlihat seperti gambar berikut.

Dalam gambar ini, nilai dinyatakan secara terpisah. Misalnya, kehadiran kelas pada hari Rabu adalah 20 sedangkan pada hari Sabtu adalah 15. Nilai-nilai ini dapat dipertimbangkan secara individu dan terpisah atau secara terpisah, oleh karena itu disebut sebagaidiscrete values.

Digit biner yang hanya memiliki 1 dan 0 kebanyakan disebut sebagai digital values. Oleh karena itu, sinyal yang mewakili 1s dan 0s juga disebut sebagaidigital signals. Komunikasi berdasarkan sinyal digital dan nilai digital disebut sebagaiDigital Communication.

Sinyal Berkala

Sinyal analog atau digital apa pun, yang mengulangi polanya selama periode waktu tertentu, disebut sebagai a Periodic Signal. Sinyal ini memiliki pola yang berulang-ulang dan mudah diasumsikan atau dihitung.

Contoh

Jika kita menganggap permesinan dalam suatu industri, proses yang berlangsung satu demi satu adalah prosedur yang berkelanjutan. Misalnya, pengadaan dan penilaian bahan mentah, pemrosesan bahan dalam batch, pengemasan muatan produk satu demi satu, dll., Mengikuti prosedur tertentu berulang kali.

Proses seperti itu apakah dianggap analog atau digital, dapat direpresentasikan secara grafis sebagai berikut.

Sinyal Aperiodik

Sinyal analog atau digital apa pun, yang tidak mengulangi polanya selama periode waktu tertentu disebut sebagai Aperiodic Signal. Sinyal ini memiliki polanya berlanjut tetapi polanya tidak berulang. Ini juga tidak mudah untuk diasumsikan atau dihitung.

Contoh

Rutinitas sehari-hari seseorang, jika diperhatikan, terdiri dari berbagai jenis pekerjaan yang membutuhkan interval waktu yang berbeda untuk tugas yang berbeda. Interval waktu atau pekerjaan tidak terus menerus berulang. Misalnya seseorang tidak akan terus menerus menyikat giginya dari pagi hingga malam, itu pun dengan jangka waktu yang sama.

Proses seperti itu apakah dianggap analog atau digital, dapat direpresentasikan secara grafis sebagai berikut.

Secara umum, sinyal yang digunakan dalam sistem komunikasi bersifat analog, yang ditransmisikan secara analog atau diubah menjadi digital dan kemudian ditransmisikan, tergantung kebutuhan.

Agar sinyal dapat ditransmisikan ke suatu jarak, tanpa pengaruh gangguan eksternal atau penambahan noise dan tanpa memudar, sinyal tersebut harus menjalani proses yang disebut sebagai Modulation. Ini meningkatkan kekuatan sinyal tanpa mengganggu parameter sinyal asli.

Apa itu Modulasi?

Sebuah pesan yang membawa sinyal harus ditransmisikan dari jarak jauh dan untuk membangun komunikasi yang andal, perlu bantuan sinyal frekuensi tinggi yang seharusnya tidak mempengaruhi karakteristik asli dari sinyal pesan tersebut.

Karakteristik sinyal pesan, jika diubah, pesan yang terkandung di dalamnya juga berubah. Oleh karena itu, sinyal pesan harus dijaga. Sinyal frekuensi tinggi dapat menempuh jarak yang lebih jauh, tanpa terpengaruh oleh gangguan eksternal. Kami mengambil bantuan dari sinyal frekuensi tinggi yang disebut sebagaicarrier signaluntuk mengirimkan sinyal pesan kami. Proses seperti itu secara sederhana disebut sebagai Modulasi.

Modulasi adalah proses mengubah parameter sinyal pembawa, sesuai dengan nilai sesaat dari sinyal modulasi.

Kebutuhan Modulasi

Sinyal pita dasar tidak kompatibel untuk transmisi langsung. Untuk sinyal seperti itu, untuk menempuh jarak yang lebih jauh, kekuatannya harus ditingkatkan dengan memodulasi dengan gelombang pembawa frekuensi tinggi, yang tidak mempengaruhi parameter sinyal modulasi.

Keuntungan Modulasi

Antena yang digunakan untuk transmisi, harus sangat besar, jika modulasi tidak dilakukan. Jangkauan komunikasi menjadi terbatas karena gelombang tidak dapat menempuh jarak tanpa terdistorsi.

Berikut adalah beberapa keuntungan dari penerapan modulasi pada sistem komunikasi.

• Pengurangan ukuran antena
• Tidak ada pencampuran sinyal
• Peningkatan jangkauan komunikasi
• Multiplexing sinyal
• Kemungkinan penyesuaian bandwidth
• Kualitas penerimaan yang lebih baik

Sinyal dalam Proses Modulasi

Berikut adalah tiga jenis sinyal dalam proses modulasi.

Pesan atau Modulasi Sinyal

Sinyal yang berisi pesan yang akan dikirim disebut sebagai a message signal. Ini adalah sinyal pita dasar, yang harus menjalani proses modulasi, untuk bisa ditransmisikan. Oleh karena itu, ini juga disebut sebagaimodulating signal.

Sinyal Pembawa

Sinyal frekuensi tinggi yang memiliki amplitudo, frekuensi dan fasa tertentu tetapi tidak mengandung informasi disebut sebagai a carrier signal. Ini adalah sinyal kosong dan digunakan untuk membawa sinyal ke penerima setelah modulasi.

Sinyal termodulasi

Sinyal yang dihasilkan setelah proses modulasi disebut sebagai a modulated signal. Sinyal ini merupakan kombinasi dari sinyal modulasi dan sinyal pembawa.

Jenis Modulasi

Ada banyak jenis modulasi. Bergantung pada teknik modulasi yang digunakan, mereka diklasifikasikan seperti yang ditunjukkan pada gambar berikut.

Jenis modulasi secara luas diklasifikasikan menjadi modulasi gelombang kontinyu dan modulasi pulsa.

Modulasi Gelombang Kontinyu

Dalam modulasi gelombang kontinu, gelombang sinus frekuensi tinggi digunakan sebagai gelombang pembawa. Ini selanjutnya dibagi menjadi modulasi amplitudo dan sudut.

• Jika amplitudo gelombang pembawa frekuensi tinggi divariasikan sesuai dengan amplitudo sesaat dari sinyal modulasi, maka teknik seperti itu disebut sebagai Amplitude Modulation.

• Jika sudut gelombang pembawa bervariasi, sesuai dengan nilai sesaat dari sinyal modulasi, maka teknik seperti itu disebut sebagai Angle Modulation. Modulasi sudut selanjutnya dibagi menjadi modulasi frekuensi dan modulasi fase.

  • Jika frekuensi gelombang pembawa bervariasi, sesuai dengan nilai sesaat dari sinyal modulasi, maka teknik seperti itu disebut sebagai Frequency Modulation.

  • Jika fase gelombang pembawa frekuensi tinggi divariasikan sesuai dengan nilai sesaat dari sinyal modulasi, maka teknik seperti itu disebut sebagai Phase Modulation.

Modulasi Pulsa

Dalam modulasi pulsa, urutan periodik pulsa persegi panjang, digunakan sebagai gelombang pembawa. Ini selanjutnya dibagi menjadi modulasi analog dan digital.

Dalam teknik modulasi analog, jika amplitudo atau durasi atau posisi pulsa divariasikan sesuai dengan nilai sesaat sinyal modulasi pita dasar, maka teknik tersebut disebut dengan Pulse Amplitude Modulation (PAM) atau Pulse Duration / Width Modulation (PDM). / PWM), atau Modulasi Posisi Pulsa (PPM).

Dalam modulasi digital teknik modulasi yang digunakan adalah Pulse Code Modulation (PCM) dimana sinyal analog diubah menjadi bentuk digital 1s dan 0s. Hasilnya adalah rangkaian pulsa berkode, ini disebut PCM. Ini dikembangkan lebih lanjut sebagai Modulasi Delta (DM). Teknik modulasi digital ini dibahas dalam tutorial Komunikasi Digital kami

Gelombang kontinu berlangsung terus menerus tanpa interval dan itu adalah sinyal pesan pita dasar, yang berisi informasi. Gelombang ini harus dimodulasi.

Menurut definisi standar, "Amplitudo sinyal pembawa bervariasi sesuai dengan amplitudo sesaat dari sinyal modulasi". Artinya, amplitudo sinyal pembawa yang tidak mengandung informasi bervariasi sesuai dengan amplitudo sinyal yang mengandung informasi, pada setiap saat. Ini dapat dijelaskan dengan baik oleh gambar-gambar berikut.

Gambar pertama menunjukkan gelombang modulasi, yang merupakan sinyal pesan. Yang berikutnya adalah gelombang pembawa, yang merupakan sinyal frekuensi tinggi dan tidak mengandung informasi. Sedangkan yang terakhir adalah gelombang termodulasi resultan.

Dapat diamati bahwa puncak positif dan negatif dari gelombang pembawa, saling berhubungan dengan garis imajiner. Garis ini membantu menciptakan bentuk yang tepat dari sinyal modulasi. Garis imajiner pada gelombang pembawa ini disebut sebagaiEnvelope. Ini sama dengan sinyal pesan.

Ekspresi Matematika

Berikut adalah ekspresi matematis untuk gelombang tersebut.

Representasi Domain Waktu dari Gelombang

Biarkan sinyal modulasi menjadi,

$$ m \ kiri (t \ kanan) = A_m \ cos \ kiri (2 \ pi f_mt \ kanan) $$

dan sinyal pembawa menjadi,

$$ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $$

Dimana,

$ A_m $ dan $ A_c $ masing-masing adalah amplitudo dari sinyal modulasi dan sinyal pembawa.

$ f_m $ dan $ f_c $ masing-masing adalah frekuensi dari sinyal modulasi dan sinyal pembawa.

Kemudian, persamaan gelombang Amplitude Modulated adalah

$ s (t) = \ kiri [A_c + A_m \ cos \ kiri (2 \ pi f_mt \ kanan) \ kanan] \ cos \ kiri (2 \ pi f_ct \ kanan) $ (Persamaan 1)

Indeks Modulasi

Gelombang pembawa, setelah dimodulasi, jika level termodulasi dihitung, maka upaya seperti itu disebut sebagai Modulation Index atau Modulation Depth. Ini menyatakan tingkat modulasi yang dialami gelombang pembawa.

Susun kembali Persamaan 1 seperti di bawah ini.

$ s (t) = A_c \ kiri [1+ \ kiri (\ frac {A_m} {A_c} \ kanan) \ cos \ kiri (2 \ pi f_mt \ kanan) \ kanan] \ cos \ kiri (2 \ pi f_ct \ benar) $

$ \ Rightarrow s \ left (t \ right) = A_c \ left [1 + \ mu \ cos \ left (2 \ pi f_m t \ right) \ kanan] \ cos \ kiri (2 \ pi f_ct \ kanan) $ ( Persamaan 2)

Di mana, $ \ mu $ adalah indeks Modulasi dan itu sama dengan rasio $ A_m $ dan $ A_c $. Secara matematis, kita bisa menulisnya sebagai

$ \ mu = \ frac {A_m} {A_c} $ (Persamaan 3)

Oleh karena itu, kita dapat menghitung nilai indeks modulasi dengan menggunakan rumus di atas, ketika amplitudo pesan dan sinyal pembawa diketahui.

Sekarang, mari kita turunkan satu rumus lagi untuk indeks modulasi dengan mempertimbangkan Persamaan 1. Kita dapat menggunakan rumus ini untuk menghitung nilai indeks modulasi, ketika amplitudo maksimum dan minimum dari gelombang termodulasi diketahui.

Misalkan $ A_ \ max $ dan $ A_ \ min $ menjadi amplitudo maksimum dan minimum dari gelombang termodulasi.

Kita akan mendapatkan amplitudo maksimum dari gelombang termodulasi, ketika $ \ cos \ left (2 \ pi f_mt \ right) $ adalah 1.

$ \ Rightarrow A_ \ max = A_c + A_m $ (Persamaan 4)

Kita akan mendapatkan amplitudo minimum dari gelombang termodulasi, ketika $ \ cos \ left (2 \ pi f_mt \ right) $ adalah -1.

$ \ Rightarrow A_ \ min = A_c - A_m $ (Persamaan 5)

Tambahkan Persamaan 4 dan Persamaan 5.

$$ A_ \ max + A_ \ min = A_c + A_m + A_c-A_m = 2A_c $$

$ \ Rightarrow A_c = \ frac {A_ \ max + A_ \ min} {2} $ (Persamaan 6)

Kurangi Persamaan 5 dari Persamaan 4.

$$ A_ \ max - A_ \ min = A_c + A_m - \ kiri (A_c -A_m \ kanan) = 2A_m $$

$ \ Rightarrow A_m = \ frac {A_ \ max - A_ \ min} {2} $ (Persamaan 7)

Rasio Persamaan 7 dan Persamaan 6 adalah sebagai berikut.

$$ \ frac {A_m} {A_c} = \ frac {\ kiri (A_ {maks} - A_ {min} \ kanan) / 2} {\ kiri (A_ {max} + A_ {min} \ kanan) / 2 } $$

$ \ Rightarrow \ mu = \ frac {A_ \ max - A_ \ min} {A_ \ max + A_ \ min} $ (Persamaan 8)

Oleh karena itu, Persamaan 3 dan Persamaan 8 adalah dua rumus untuk indeks Modulasi. Indeks modulasi atau kedalaman modulasi sering dilambangkan dalam persentase yang disebut Persentase Modulasi. Kami akan mendapatkanpercentage of modulation, hanya dengan mengalikan nilai indeks modulasi dengan 100.

Untuk modulasi yang sempurna, nilai indeks modulasi harus 1, yang berarti persentase modulasi harus 100%.

Misalnya, jika nilai ini kurang dari 1, yaitu indeks modulasi adalah 0,5, maka keluaran termodulasi akan terlihat seperti gambar berikut. Ini disebut sebagaiUnder-modulation. Gelombang seperti itu disebut sebagaiunder-modulated wave.

Jika nilai indeks modulasi lebih besar dari 1, yaitu 1,5 atau lebih, maka gelombang akan menjadi over-modulated wave. Ini akan terlihat seperti gambar berikut.

Sebagai nilai modulasi indeks meningkat, pembawa mengalami 180 ^o pembalikan fase, yang menyebabkan sidebands tambahan dan karenanya, gelombang terdistorsi. Gelombang yang terlalu termodulasi menyebabkan interferensi, yang tidak dapat dihilangkan.

Bandwidth Gelombang AM

Bandwidth(BW) adalah perbedaan antara frekuensi sinyal tertinggi dan terendah. Secara matematis, kita bisa menulisnya sebagai

$$ BW = f_ {maks} - f_ {min} $$

Perhatikan persamaan gelombang termodulasi amplitudo berikut.

$$ s \ kiri (t \ kanan) = A_c \ kiri [1 + \ mu \ cos \ kiri (2 \ pi f_m t \ kanan) \ kanan] \ cos \ kiri (2 \ pi f_ct \ kanan) $$

$$ \ Panah kanan s \ kiri (t \ kanan) = A_c \ cos \ kiri (2 \ pi f_ct \ kanan) + A_c \ mu \ cos (2 \ pi f_ct) \ cos \ kiri (2 \ pi f_mt \ kanan) $$

$ \ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) + \ frac {A_c \ mu} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ kanan) t \ kanan] + \ frac {A_c \ mu} {2} \ cos \ kiri [2 \ pi \ kiri (f_c-f_m \ kanan) t \ kanan] $

Oleh karena itu, gelombang termodulasi amplitudo memiliki tiga frekuensi. Itu adalah frekuensi pembawa $ f_c $, frekuensi sideband atas $ f_c + f_m $ dan frekuensi sideband bawah $ f_c-f_m $

Sini,

$ f_ {max} = f_c + f_m $ dan $ f_ {min} = f_c-f_m $

Gantikan, nilai $ f_ {max} $ dan $ f_ {min} $ dalam rumus bandwidth.

$$ BW = f_c + f_m- \ kiri (f_c-f_m \ kanan) $$

$$ \ Rightarrow BW = 2f_m $$

Dengan demikian, dapat dikatakan bahwa bandwidth yang dibutuhkan untuk gelombang termodulasi amplitudo adalah dua kali frekuensi sinyal modulasi.

Perhitungan Daya Gelombang AM

Perhatikan persamaan gelombang termodulasi amplitudo berikut.

$ \ s \ kiri (t \ kanan) = A_c \ cos \ kiri (2 \ pi f_ct \ kanan) + \ frac {A_c \ mu} {2} \ cos \ kiri [2 \ pi \ kiri (f_c + f_m \ kanan) t \ kanan] + \ frac {A_c \ mu} {2} \ cos \ kiri [2 \ pi \ kiri (f_c-f_m \ kanan) t \ kanan] $

Kekuatan gelombang AM sama dengan penjumlahan dari kekuatan carrier, upper sideband, dan komponen frekuensi sideband bawah.

$$ P_t = P_c + P_ {USB} + P_ {LSB} $$

Kita tahu bahwa rumus standar untuk kekuatan sinyal cos adalah

$$ P = \ frac {{v_ {rms}} ^ {2}} {R} = \ frac {\ left (v_m / \ sqrt {2} \ right) ^ 2} {2} $$

Dimana,

$ v_ {rms} $ adalah nilai rms dari sinyal cos.

$ v_m $ adalah nilai puncak dari sinyal cos.

Pertama, mari kita temukan kekuatan pengangkut, sideband atas dan bawah satu per satu.

Kekuatan pembawa

$$ P_c = \ frac {\ left (A_c / \ sqrt {2} \ right) ^ 2} {R} = \ frac {{A_ {c}} ^ {2}} {2R} $$

Kekuatan sideband atas

$$ P_ {USB} = \ frac {\ kiri (A_c \ mu / 2 \ sqrt {2} \ kanan) ^ 2} {R} = \ frac {{A_ {c}} ^ {2} {_ {\ mu}} ^ {2}} {8R} $$

Demikian pula, kita akan mendapatkan daya pita samping bawah yang sama dengan daya pita sisi atas.

$$ P_ {LSB} = \ frac {{A_ {c}} ^ {2} {_ {\ mu}} ^ {2}} {8R} $$

Sekarang, mari kita tambahkan ketiga kekuatan ini untuk mendapatkan kekuatan gelombang AM.

$$ P_t = \ frac {{A_ {c}} ^ {2}} {2R} + \ frac {{A_ {c}} ^ {2} {_ {\ mu}} ^ {2}} {8R} + \ frac {{A_ {c}} ^ {2} {_ {\ mu}} ^ {2}} {8R} $$

$$ \ Rightarrow P_t = \ left (\ frac {{A_ {c}} ^ {2}} {2R} \ right) \ left (1+ \ frac {\ mu ^ 2} {4} + \ frac {\ mu ^ 2} {4} \ kanan) $$

$$ \ Rightarrow P_t = P_c \ kiri (1+ \ frac {\ mu ^ 2} {2} \ kanan) $$

Kita dapat menggunakan rumus di atas untuk menghitung kekuatan gelombang AM, ketika daya pembawa dan indeks modulasi diketahui.

Jika indeks modulasi $ \ mu = 1 $ maka kekuatan gelombang AM sama dengan 1,5 kali daya pembawa. Jadi, daya yang dibutuhkan untuk mentransmisikan gelombang AM adalah 1,5 kali daya pembawa untuk modulasi yang sempurna.

Pada bab sebelumnya, kita telah membahas parameter yang digunakan dalam Modulasi Amplitudo. Setiap parameter memiliki rumusnya sendiri. Dengan menggunakan rumus tersebut, kita dapat menemukan nilai parameter masing-masing. Dalam bab ini, mari kita pecahkan beberapa masalah berdasarkan konsep modulasi amplitudo.

Masalah 1

Sinyal modulasi $ m \ left (t \ right) = 10 \ cos \ left (2 \ pi \ times 10 ^ 3 t \ right) $ adalah amplitudo yang dimodulasi dengan sinyal pembawa $ c \ left (t \ right) = 50 \ cos \ kiri (2 \ pi \ times 10 ^ 5 t \ kanan) $. Temukan indeks modulasi, daya pembawa, dan daya yang dibutuhkan untuk mentransmisikan gelombang AM.

Larutan

Diberikan, persamaan sinyal modulasi sebagai

$$ m \ kiri (t \ kanan) = 10 \ cos \ kiri (2 \ pi \ times 10 ^ 3 t \ kanan) $$

Kita tahu persamaan standar sinyal modulasi sebagai

$$ m \ kiri (t \ kanan) = A_m \ cos \ kiri (2 \ pi f_mt \ kanan) $$

Dengan membandingkan dua persamaan di atas, kita akan mendapatkan

Amplitudo sinyal modulasi sebagai $ A_m = 10 volt $

dan Frekuensi sinyal modulasi sebagai $$ f_m = 10 ^ 3 Hz = 1 KHz $$

Diketahui, persamaan sinyal pembawa adalah

$$ c \ kiri (t \ kanan) = 50 \ cos \ kiri (2 \ pi \ times 10 ^ 5t \ kanan) $$

Persamaan standar sinyal pembawa adalah

$$ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $$

Dengan membandingkan kedua persamaan ini, kita akan mendapatkan

Amplitudo sinyal pembawa sebagai $ A_c = 50volts $

dan Frekuensi sinyal pembawa sebagai $ f_c = 10 ^ 5 Hz = 100 KHz $

Kita tahu rumus indeks modulasi sebagai

$$ \ mu = \ frac {A_m} {A_c} $$

Gantikan, nilai $ A_m $ dan $ A_c $ dalam rumus di atas.

$$ \ mu = \ frac {10} {50} = 0,2 $$

Oleh karena itu, nilai modulation index is 0.2 dan persentase modulasi adalah 20%.

Rumus untuk Carrier power, $ P_c = $ adalah

$$ P_c = \ frac {{A_ {c}} ^ {2}} {2R} $$

Asumsikan $ R = 1 \ Omega $ dan gantikan $ A_c $ nilai dalam rumus di atas.

$$ P_c = \ frac {\ kiri (50 \ kanan) ^ 2} {2 \ kiri (1 \ kanan)} = 1250W $$

Oleh karena itu, Carrier power, $ P_c $ adalah 1250 watts.

Kami tahu rumusnya power dibutuhkan untuk transmitting AM gelombang

$$ \ Rightarrow P_t = P_c \ kiri (1+ \ frac {\ mu ^ 2} {2} \ kanan) $$

Gantikan nilai $ P_c $ dan $ \ mu $ dalam rumus di atas.

$$ P_t = 1250 \ kiri (1+ \ frac {\ kiri (0,2 \ kanan) ^ 2} {2} \ kanan) = 1275W $$

Oleh karena itu, power required for transmitting AM gelombang 1275 watts.

Masalah 2

Persamaan gelombang amplitudo diberikan oleh $ s \ left (t \ right) = 20 \ left [1 + 0.8 \ cos \ left (2 \ pi \ times 10 ^ 3t \ right) \ right] \ cos \ left (4 \ pi \ times 10 ^ 5t \ kanan) $. Temukan daya pembawa, total daya pita samping, dan lebar pita gelombang AM.

Larutan

Diketahui, persamaan gelombang termodulasi Amplitudo adalah

$$ s \ kiri (t \ kanan) = 20 \ kiri [1 + 0,8 \ cos \ kiri (2 \ pi \ times 10 ^ 3t \ kanan) \ kanan] \ cos \ kiri (4 \ pi \ times 10 ^ 5t \ benar) $$

Tulis ulang persamaan di atas sebagai

$$ s \ kiri (t \ kanan) = 20 \ kiri [1 + 0,8 \ cos \ kiri (2 \ pi \ times 10 ^ 3t \ kanan) \ kanan] \ cos \ kiri (2 \ pi \ times 2 \ times 10 ^ 5t \ kanan) $$

Kita tahu persamaan gelombang termodulasi Amplitudo adalah

$$ s \ kiri (t \ kanan) = A_c \ kiri [1+ \ mu \ cos \ kiri (2 \ pi f_mt \ kanan) \ kanan] \ cos \ kiri (2 \ pi f_ct \ kanan) $$

Dengan membandingkan dua persamaan di atas, kita akan mendapatkan

Amplitudo sinyal pembawa sebagai $ A_c = 20 volt $

Indeks modulasi sebagai $ \ mu = 0,8 $

Frekuensi sinyal modulasi sebagai $ f_m = 10 ^ 3Hz = 1 KHz $

Frekuensi sinyal pembawa sebagai $ f_c = 2 \ times 10 ^ 5Hz = 200KHz $

Rumus kekuatan pembawa, $ P_c $ adalah

$$ P_c = \ frac {{A_ {e}} ^ {2}} {2R} $$

Asumsikan $ R = 1 \ Omega $ dan gantikan $ A_c $ nilai dalam rumus di atas.

$$ P_c = \ frac {\ kiri (20 \ kanan) ^ 2} {2 \ kiri (1 \ kanan)} = 200W $$

Oleh karena itu, Carrier power, $ P_c $ adalah 200watts.

Kita tahu rumus kekuatan pita samping total

$$ P_ {SB} = \ frac {P_c \ mu ^ 2} {2} $$

Gantikan nilai $ P_c $ dan $ \ mu $ dalam rumus di atas.

$$ P_ {SB} = \ frac {200 \ times \ kiri (0.8 \ kanan) ^ 2} {2} = 64W $$

Oleh karena itu, total side band power adalah 64 watts.

Kita tahu rumus bandwidth gelombang AM ini

$$ BW = 2f_m $$

Gantikan $ f_m $ value dalam rumus di atas.

$$ BW = 2 \ kiri (1K \ kanan) = 2 KHz $$

Oleh karena itu, bandwidth gelombang AM adalah 2 KHz.

Pada bab ini, mari kita bahas tentang modulator, yang menghasilkan gelombang termodulasi amplitudo. Dua modulator berikut menghasilkan gelombang AM.

• Modulator hukum persegi
• Mengganti modulator

Modulator Hukum Persegi

Berikut adalah diagram blok modulator hukum kuadrat

Biarkan sinyal modulasi dan pembawa dilambangkan sebagai $ m \ left (t \ right) $ dan $ A \ cos \ left (2 \ pi f_ct \ right) $ masing-masing. Kedua sinyal ini diterapkan sebagai input ke blok musim panas (penambah). Blok musim panas ini menghasilkan keluaran, yaitu penambahan modulasi dan sinyal pembawa. Secara matematis, kita bisa menulisnya sebagai

$$ V_1t = m \ kiri (t \ kanan) + A_c \ cos \ kiri (2 \ pi f_ct \ kanan) $$

Sinyal $ V_1t $ ini diterapkan sebagai masukan ke perangkat nonlinier seperti dioda. Ciri-ciri dioda berkaitan erat dengan hukum kuadrat.

$ V_2t = k_1V_1 \ kiri (t \ kanan) + k_2V_1 ^ 2 \ kiri (t \ kanan) $ (Persamaan 1)

Di mana, $ k_1 $ dan $ k_2 $ adalah konstanta.

Gantikan $ V_1 \ kiri (t \ kanan) $ pada Persamaan 1

$$ V_2 \ kiri (t \ kanan) = k_1 \ kiri [m \ kiri (t \ kanan) + A_c \ cos \ kiri (2 \ pi f_ct \ kanan) \ kanan] + k_2 \ kiri [m \ kiri (t \ kanan) + A_c \ cos \ kiri (2 \ pi f_ct \ kanan) \ kanan] ^ 2 $$

$ \ Kananarrow V_2 \ kiri (t \ kanan) = k_1 m \ kiri (t \ kanan) + k_1 A_c \ cos \ kiri (2 \ pi f_ct \ kanan) + k_2 m ^ 2 \ kiri (t \ kanan) + $

$ k_2A_c ^ 2 \ cos ^ 2 \ kiri (2 \ pi f_ct \ kanan) + 2k_2m \ kiri (t \ kanan) A_c \ cos \ kiri (2 \ pi f_ct \ kanan) $

$ \ Kananarrow V_2 \ kiri (t \ kanan) = k_1 m \ kiri (t \ kanan) + k_2 m ^ 2 \ kiri (t \ kanan) + k_2 A ^ 2_c \ cos ^ 2 \ kiri (2 \ pi f_ct \ kanan) + $

$ k_1A_c \ kiri [1+ \ kiri (\ frac {2k_2} {k_1} \ kanan) m \ kiri (t \ kanan) \ kanan] \ cos \ kiri (2 \ pi f_ct \ kanan) $

Suku terakhir dari persamaan di atas mewakili gelombang AM yang diinginkan dan tiga suku pertama dari persamaan di atas tidak diinginkan. Jadi, dengan bantuan band pass filter, kita hanya bisa melewatkan gelombang AM dan menghilangkan tiga suku pertama.

Oleh karena itu, keluaran modulator hukum kuadrat adalah

$$ s \ kiri (t \ kanan) = k_1A_c \ kiri [1+ \ kiri (\ frac {2k_2} {k_1} \ kanan) m \ kiri (t \ kanan) \ kanan] \ cos \ kiri (2 \ pi f_ct \ kanan) $$

Persamaan standar gelombang AM adalah

$$ s \ kiri (t \ kanan) = A_c \ kiri [1 + k_am \ kiri (t \ kanan) \ kanan] \ cos \ kiri (2 \ pi f_ct \ kanan) $$

Dimana, $ K_a $ adalah sensitivitas amplitudo

Dengan membandingkan keluaran modulator hukum kuadrat dengan persamaan standar gelombang AM, kita akan mendapatkan faktor penskalaan sebagai $ k_1 $ dan sensitivitas amplitudo $ k_a $ sebagai $ \ frac {2k_2} {k1} $.

Mengalihkan Modulator

Berikut adalah diagram blok modulator switching.

Modulator switching mirip dengan modulator hukum kuadrat. Satu-satunya perbedaan adalah bahwa dalam modulator hukum kuadrat, dioda dioperasikan dalam mode non-linier, sedangkan pada modulator switching, dioda harus beroperasi sebagai sakelar yang ideal.

Biarkan sinyal modulasi dan pembawa dilambangkan sebagai $ m \ left (t \ right) $ dan $ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $ masing-masing. Kedua sinyal ini diterapkan sebagai input ke blok musim panas (penambah). Blok musim panas menghasilkan keluaran, yaitu penambahan sinyal modulasi dan pembawa. Secara matematis, kita bisa menulisnya sebagai

$$ V_1 \ kiri (t \ kanan) = m \ kiri (t \ kanan) + c \ kiri (t \ kanan) = m \ kiri (t \ kanan) + A_c \ cos \ kiri (2 \ pi f_ct \ kanan ) $$

Sinyal ini $ V_1 \ kiri (t \ kanan) $ diterapkan sebagai input dioda. Asumsikan, besarnya sinyal modulasi sangat kecil jika dibandingkan dengan amplitudo sinyal pembawa $ A_c $. Jadi, aksi ON dan OFF dioda dikendalikan oleh sinyal pembawa $ c \ left (t \ right) $. Artinya, dioda akan bias maju ketika $ c \ left (t \ right)> 0 $ dan akan reverse bias ketika $ c \ left (t \ right) <0 $.

Oleh karena itu, keluaran dari dioda adalah

$$ V_2 \ kiri (t \ kanan) = \ kiri \ {\ mulai {matriks} V_1 \ kiri (t \ kanan) & jika & c \ kiri (t \ kanan)> 0 \\ 0 & jika & c \ kiri (t \ kanan) <0 \ end {matrix} \ right. $$

Kami dapat memperkirakan ini sebagai

$ V_2 \ kiri (t \ kanan) = V_1 \ kiri (t \ kanan) x \ kiri (t \ kanan) $ (Persamaan 2)

Di mana, $ x \ left (t \ right) $ adalah kereta pulsa periodik dengan periode waktu $ T = \ frac {1} {f_c} $

Representasi deret Fourier dari rangkaian pulsa periodik ini adalah

$$ x \ left (t \ right) = \ frac {1} {2} + \ frac {2} {\ pi} \ sum_ {n = 1} ^ {\ infty} \ frac {\ left (-1 \ kanan) ^ n-1} {2n-1} \ cos \ left (2 \ pi \ left (2n-1 \ right) f_ct \ right) $$

$$ \ Rightarrow x \ left (t \ right) = \ frac {1} {2} + \ frac {2} {\ pi} \ cos \ left (2 \ pi f_ct \ right) - \ frac {2} { 3 \ pi} \ cos \ kiri (6 \ pi f_ct \ kanan) + .... $$

Gantikan, nilai $ V_1 \ kiri (t \ kanan) $ dan $ x \ kiri (t \ kanan) $ dalam Persamaan 2.

$ V_2 \ kiri (t \ kanan) = \ kiri [m \ kiri (t \ kanan) + A_c \ cos \ kiri (2 \ pi f_ct \ kanan) \ kanan] \ kiri [\ frac {1} {2} + \ frac {2} {\ pi} \ cos \ left (2 \ pi f_ct \ right) - \ frac {2} {3 \ pi} \ cos \ left (6 \ pi f_ct \ right) + ..... \ benar] $

$ V_2 \ kiri (t \ kanan) = \ frac {m \ kiri (t \ kanan)} {2} + \ frac {A_c} {2} \ cos \ kiri (2 \ pi f_ct \ kanan) + \ frac { 2m \ kiri (t \ kanan)} {\ pi} \ cos \ kiri (2 \ pi f_ct \ kanan) + \ frac {2A_c} {\ pi} \ cos ^ 2 \ kiri (2 \ pi f_ct \ kanan) - $

$ \ frac {2m \ left (t \ right)} {3 \ pi} \ cos \ left (6 \ pi f_ct \ right) - \ frac {2A_c} {3 \ pi} \ cos \ left (2 \ pi f_ct \ kanan) \ cos \ kiri (6 \ pi f_ct \ kanan) + ..... $

$ V_2 \ kiri (t \ kanan) = \ frac {A_c} {2} \ kiri (1+ \ kiri (\ frac {4} {\ pi A_c} \ kanan) m \ kiri (t \ kanan) \ kanan) \ cos \ kiri (2 \ pi f_ct \ kanan) + \ frac {m \ kiri (t \ kanan)} {2} + \ frac {2A_c} {\ pi} \ cos ^ 2 \ kiri (2 \ pi f_ct \ benar) - $

$ \ frac {2m \ left (t \ right)} {3 \ pi} \ cos \ left (6 \ pi f_ct \ right) - \ frac {2A_c} {3 \ pi} \ cos \ left (2 \ pi f_ct \ kanan) \ cos \ kiri (6 \ pi f_ct \ kanan) + ..... $

1 ^st jangka dari persamaan di atas merupakan gelombang AM yang diinginkan dan istilah yang tersisa adalah istilah yang tidak diinginkan. Jadi, dengan bantuan band pass filter, kita hanya dapat melewatkan gelombang AM dan menghilangkan istilah yang tersisa.

Oleh karena itu, keluaran dari modulator switching adalah

$$ s \ kiri (t \ kanan) = \ frac {A_c} {2} \ kiri (1+ \ kiri (\ frac {4} {\ pi A_c} \ kanan) m \ kiri (t \ kanan) \ kanan ) \ cos \ left (2 \ pi f_ct \ right) $$

Kita tahu persamaan standar gelombang AM adalah

$$ s \ kiri (t \ kanan) = A_c \ kiri [1 + k_am \ kiri (t \ kanan) \ kanan] \ cos \ kiri (2 \ pi f_ct \ kanan) $$

Di mana, $ k_a $ adalah sensitivitas amplitudo.

Dengan membandingkan keluaran modulator switching dengan persamaan standar gelombang AM, kita akan mendapatkan faktor skala sebagai 0.5 dan sensitivitas amplitudo $ k_a $ sebagai $ \ frac {4} {\ pi A_c} $.

Proses mengekstraksi sinyal pesan asli dari gelombang termodulasi dikenal sebagai detection atau demodulation. Sirkuit, yang mendemodulasi gelombang termodulasi dikenal sebagaidemodulator. Demodulator (detektor) berikut digunakan untuk mendemodulasi gelombang AM.

• Demodulator Hukum Persegi
• Detektor Amplop

Demodulator Hukum Persegi

Demodulator hukum persegi digunakan untuk mendemodulasi gelombang AM tingkat rendah. Berikut adalah diagram blok darisquare law demodulator.

Demodulator ini berisi perangkat hukum kuadrat dan filter akses rendah. Gelombang AM $ V_1 \ kiri (t \ kanan) $ diterapkan sebagai masukan untuk demodulator ini.

Bentuk standar gelombang AM adalah

$$ V_1 \ kiri (t \ kanan) = A_c \ kiri [1 + k_am \ kiri (t \ kanan) \ kanan] \ cos \ kiri (2 \ pi f_ct \ kanan) $$

Kita tahu bahwa hubungan matematis antara input dan output perangkat hukum kuadrat adalah

$ V_2 \ kiri (t \ kanan) = k_1V_1 \ kiri (t \ kanan) + k_2V_1 ^ 2 \ kiri (t \ kanan) $ (Persamaan 1)

Dimana,

$ V_1 \ kiri (t \ kanan) $ adalah masukan dari perangkat hukum kuadrat, yang tidak lain adalah gelombang AM

$ V_2 \ kiri (t \ kanan) $ adalah keluaran dari perangkat hukum kuadrat

$ k_1 $ dan $ k_2 $ adalah konstanta

Gantikan $ V_1 \ kiri (t \ kanan) $ pada Persamaan 1

$$ V_2 \ kiri (t \ kanan) = k_1 \ kiri (A_c \ kiri [1 + k_am \ kiri (t \ kanan) \ kanan] \ cos \ kiri (2 \ pi f_ct \ kanan) \ kanan) + k_2 \ kiri (A_c \ kiri [1 + k_am \ kiri (t \ kanan) \ kanan] \ cos \ kiri (2 \ pi f_ct \ kanan) \ kanan) ^ 2 $$

$ \ Kananarrow V_2 \ kiri (t \ kanan) = k_1A_c \ cos \ kiri (2 \ pi f_ct \ kanan) + k_1A_ck_am \ kiri (t \ kanan) \ cos \ kiri (2 \ pi f_ct \ kanan) + $

$ k_2 {A_ {c}} ^ {2} \ kiri [1+ {K_ {a}} ^ {2} m ^ 2 \ kiri (t \ kanan) + 2k_am \ kiri (t \ kanan) \ kanan] \ kiri (\ frac {1+ \ cos \ left (4 \ pi f_ct \ right)} {2} \ kanan) $

$ \ Rightarrow V_2 \ left (t \ right) = k_1A_c \ cos \ left (2 \ pi f_ct \ right) + k_1A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) + \ frac { K_2 {A_ {c}} ^ {2}} {2} + $

$ \ frac {K_2 {A_ {c}} ^ {2}} {2} \ cos \ left (4 \ pi f_ct \ right) + \ frac {k_2 {A_ {c}} ^ {2} {k_ {a }} ^ {2} m ^ 2 \ kiri (t \ kanan)} {2} + \ frac {k_2 {A_ {c}} ^ {2} {k_ {a}} ^ {2} m ^ 2 \ kiri (t \ kanan)} {2} \ cos \ kiri (4 \ pi f_ct \ kanan) + $

$ k_2 {A_ {c}} ^ {2} k_am \ kiri (t \ kanan) + k_2 {A_ {c}} ^ {2} k_am \ kiri (t \ kanan) \ cos \ kiri (4 \ pi f_ct \ benar) $

Dalam persamaan di atas, istilah $ k_2 {A_ {c}} ^ {2} k_am \ left (t \ right) $ adalah versi berskala dari sinyal pesan. Ini dapat diekstraksi dengan melewatkan sinyal di atas melalui filter lolos rendah dan komponen DC $ \ frac {k_2 {A_ {c}} ^ {2}} {2} $ dapat dihilangkan dengan bantuan kapasitor kopling.

Detektor Amplop

Detektor amplop digunakan untuk mendeteksi (mendemodulasi) gelombang AM tingkat tinggi. Berikut ini adalah diagram blok dari detektor amplop.

Detektor envelope ini terdiri dari dioda dan low pass filter. Di sini, dioda adalah elemen pendeteksi utama. Oleh karena itu, detektor amplop juga disebut sebagaidiode detector. Filter low pass berisi kombinasi paralel resistor dan kapasitor.

Gelombang AM $ s \ kiri (t \ kanan) $ diterapkan sebagai masukan untuk detektor ini.

Kita tahu bentuk standar gelombang AM adalah

$$ s \ kiri (t \ kanan) = A_c \ kiri [1 + k_am \ kiri (t \ kanan) \ kanan] \ cos \ kiri (2 \ pi f_ct \ kanan) $$

Dalam setengah siklus positif gelombang AM, dioda bekerja dan kapasitor mengisi ke nilai puncak gelombang AM. Ketika nilai gelombang AM kurang dari nilai ini, dioda akan dibiaskan terbalik. Dengan demikian, kapasitor akan keluar melalui resistorRsampai setengah siklus positif gelombang AM berikutnya. Ketika nilai gelombang AM lebih besar dari tegangan kapasitor, dioda bekerja dan prosesnya akan diulang.

Kita harus memilih nilai komponen sedemikian rupa sehingga kapasitor mengisi daya dengan sangat cepat dan habis dengan sangat lambat. Hasilnya, kita akan mendapatkan bentuk gelombang tegangan kapasitor yang sama dengan gelombang amplop AM, yang hampir mirip dengan sinyal modulasi.

Dalam proses Modulasi Amplitudo, gelombang termodulasi terdiri dari gelombang pembawa dan dua buah sideband. Gelombang termodulasi memiliki informasi hanya di sidebands.Sideband tidak lain adalah pita frekuensi, yang mengandung daya, yang merupakan frekuensi yang lebih rendah dan lebih tinggi dari frekuensi pembawa.

Transmisi sinyal, yang berisi pembawa bersama dengan dua sideband dapat disebut sebagai Double Sideband Full Carrier sistem atau sederhana DSBFC. Itu diplot seperti yang ditunjukkan pada gambar berikut.

Namun, transmisi seperti itu tidak efisien. Karena, dua pertiga dari daya disia-siakan di kapal induk, yang tidak membawa informasi.

Jika pembawa ini ditekan dan daya yang disimpan didistribusikan ke dua sideband, maka proses seperti itu disebut sebagai Double Sideband Suppressed Carrier sistem atau sederhana DSBSC. Itu diplot seperti yang ditunjukkan pada gambar berikut.

Ekspresi Matematika

Mari kita pertimbangkan ekspresi matematika yang sama untuk modulasi dan sinyal pembawa seperti yang telah kita bahas di bab-bab sebelumnya.

yaitu, Modulasi sinyal

$$ m \ kiri (t \ kanan) = A_m \ cos \ kiri (2 \ pi f_mt \ kanan) $$

Sinyal pembawa

$$ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $$

Secara matematis, kita dapat merepresentasikan equation of DSBSC wave sebagai produk modulasi dan sinyal pembawa.

$$ s \ kiri (t \ kanan) = m \ kiri (t \ kanan) c \ kiri (t \ kanan) $$

$$ \ Panah kanan s \ kiri (t \ kanan) = A_mA_c \ cos \ kiri (2 \ pi f_mt \ kanan) \ cos \ kiri (2 \ pi f_ct \ kanan) $$

Bandwidth Gelombang DSBSC

Kita tahu rumus bandwidth (BW) ini

$$ BW = f_ {max} -f_ {min} $$

Perhatikan persamaan gelombang termodulasi DSBSC.

$$ s \ kiri (t \ kanan) = A_mA_c \ cos \ kiri (2 \ pi f_mt \ kanan) \ cos (2 \ pi f_ct) $$

$$ \ Rightarrow s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] + \ frac {A_mA_c} {2 } \ cos \ kiri [2 \ pi \ kiri (f_c-f_m \ kanan) t \ kanan] $$

Gelombang termodulasi DSBSC hanya memiliki dua frekuensi. Jadi, frekuensi maksimum dan minimum masing-masing adalah $ f_c + f_m $ dan $ f_c-f_m $.

yaitu,

$ f_ {max} = f_c + f_m $ dan $ f_ {min} = f_c-f_m $

Gantikan, nilai $ f_ {max} $ dan $ f_ {min} $ dalam rumus bandwidth.

$$ BW = f_c + f_m- \ kiri (f_c-f_m \ kanan) $$

$$ \ Rightarrow BW = 2f_m $$

Jadi, bandwidth gelombang DSBSC sama dengan gelombang AM dan sama dengan dua kali frekuensi sinyal modulasi.

Perhitungan Daya Gelombang DSBSC

Perhatikan persamaan gelombang termodulasi DSBSC berikut ini.

$$ s \ kiri (t \ kanan) = \ frac {A_mA_c} {2} \ cos \ kiri [2 \ pi \ kiri (f_c + f_m \ kanan) t \ kanan] + \ frac {A_mA_c} {2} \ cos \ kiri [2 \ pi \ kiri (f_c-f_m \ kanan) t \ kanan] $$

Kekuatan gelombang DSBSC sama dengan jumlah kekuatan komponen frekuensi pita samping atas dan pita samping bawah.

$$ P_t = P_ {USB} + P_ {LSB} $$

Kita tahu rumus standar untuk kekuatan sinyal cos adalah

$$ P = \ frac {{v_ {rms}} ^ {2}} {R} = \ frac {\ left (v_m \ sqrt {2} \ right) ^ 2} {R} $$

Pertama, mari kita temukan kekuatan sideband atas dan sideband bawah satu per satu.

Kekuatan sideband atas

$$ P_ {USB} = \ frac {\ left (A_mA_c / 2 \ sqrt {2} \ right) ^ 2} {R} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8R} $$

Demikian pula, kita akan mendapatkan daya sideband bawah yang sama dengan daya sideband atas.

$$ P_ {USB} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8R} $$

Sekarang, mari kita tambahkan dua kekuatan sideband ini untuk mendapatkan kekuatan gelombang DSBSC.

$$ P_t = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8R} + \ frac {{A_ {m}} ^ {2} {A_ {c} } ^ {2}} {8R} $$

$$ \ Rightarrow P_t = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {4R} $$

Oleh karena itu, daya yang dibutuhkan untuk mentransmisikan gelombang DSBSC sama dengan daya kedua sideband.

Pada bab ini, mari kita bahas tentang modulator yang menghasilkan gelombang DSBSC. Dua modulator berikut menghasilkan gelombang DSBSC.

• Modulator yang seimbang
• Modulator cincin

Modulator Seimbang

Berikut adalah diagram blok dari Balanced modulator.

Balanced modulatorterdiri dari dua modulator AM yang identik. Kedua modulator ini disusun dalam konfigurasi yang seimbang untuk menekan sinyal pembawa. Oleh karena itu, ini disebut modulator Seimbang.

Sinyal pembawa yang sama $ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $ diterapkan sebagai salah satu input ke dua modulator AM ini. Sinyal modulasi $ m \ left (t \ right) $ diterapkan sebagai input lain ke modulator AM atas. Sedangkan sinyal modulasi $ m \ left (t \ right) $ dengan polaritas berlawanan, yaitu $ -m \ left (t \ right) $ digunakan sebagai input lain untuk modulator AM bawah.

Output dari modulator AM atas adalah

$$ s_1 \ kiri (t \ kanan) = A_c \ kiri [1 + k_am \ kiri (t \ kanan) \ kanan] \ cos \ kiri (2 \ pi f_ct \ kanan) $$

Output dari modulator AM yang lebih rendah adalah

$$ s_2 \ kiri (t \ kanan) = A_c \ kiri [1-k_am \ kiri (t \ kanan) \ kanan] \ cos \ kiri (2 \ pi f_ct \ kanan) $$

Kami mendapatkan gelombang DSBSC $ s \ kiri (t \ kanan) $ dengan mengurangi $ s_2 \ kiri (t \ kanan) $ dari $ s_1 \ kiri (t \ kanan) $. Blok musim panas digunakan untuk melakukan operasi ini. $ s_1 \ kiri (t \ kanan) $ dengan tanda positif dan $ s_2 \ kiri (t \ kanan) $ dengan tanda negatif diterapkan sebagai masukan untuk blok musim panas. Jadi, blok musim panas menghasilkan keluaran $ s \ kiri (t \ kanan) $ yang merupakan selisih dari $ s_1 \ kiri (t \ kanan) $ dan $ s_2 \ kiri (t \ kanan) $.

$$ \ Rightarrow s \ left (t \ right) = A_c \ kiri [1 + k_am \ kiri (t \ kanan) \ kanan] \ cos \ kiri (2 \ pi f_ct \ kanan) -A_c \ kiri [1-k_am \ kiri (t \ kanan) \ kanan] \ cos \ kiri (2 \ pi f_ct \ kanan) $$

$$ \ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) + A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) - A_c \ cos \ left (2 \ pi f_ct \ right) + $$

$ A_ck_am \ kiri (t \ kanan) \ cos \ kiri (2 \ pi f_ct \ kanan) $

$ \ Rightarrow s \ left (t \ right) = 2A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) $

Kita tahu persamaan standar gelombang DSBSC adalah

$$ s \ kiri (t \ kanan) = A_cm \ kiri (t \ kanan) \ cos \ kiri (2 \ pi f_ct \ kanan) $$

Dengan membandingkan keluaran blok musim panas dengan persamaan standar gelombang DSBSC, kita akan mendapatkan faktor penskalaan sebagai $ 2k_a $

Modulator Cincin

Berikut adalah diagram blok modulator Ring.

Dalam diagram ini, empat dioda $ D_1 $, $ D_2 $, $ D_3 $ dan $ D_4 $ dihubungkan dalam struktur cincin. Oleh karena itu, modulator ini disebut sebagairing modulator. Dua trafo center tap digunakan dalam diagram ini. Sinyal pesan $ m \ kiri (t \ kanan) $ diterapkan ke transformator masukan. Sedangkan, pembawa sinyal $ c \ left (t \ right) $ diterapkan di antara dua trafo center tap.

Untuk setengah siklus positif dari sinyal pembawa, dioda $ D_1 $ dan $ D_3 $ DIAKTIFKAN dan dua dioda lainnya $ D_2 $ dan $ D_4 $ dimatikan. Dalam hal ini, sinyal pesan dikalikan dengan +1.

Untuk setengah siklus negatif dari sinyal pembawa, dioda $ D_2 $ dan $ D_4 $ DIAKTIFKAN dan dua dioda lainnya $ D_1 $ dan $ D_3 $ dimatikan. Dalam hal ini, sinyal pesan dikalikan dengan -1. Ini menghasilkan pergeseran fasa $ 180 ^ 0 $ dalam gelombang DSBSC yang dihasilkan.

Dari analisis di atas, kita dapat mengatakan bahwa empat dioda $ D_1 $, $ D_2 $, $ D_3 $ dan $ D_4 $ dikendalikan oleh sinyal pembawa. Jika pembawa adalah gelombang persegi, maka representasi deret Fourier dari $ c \ left (t \ right) $ direpresentasikan sebagai

$$ c \ left (t \ right) = \ frac {4} {\ pi} \ sum_ {n = 1} ^ {\ infty} \ frac {\ left (-1 \ right) ^ {n-1}} {2n-1} \ cos \ kiri [2 \ pi f_ct \ kiri (2n-1 \ kanan) \ kanan] $$

Kita akan mendapatkan gelombang DSBSC $ s \ left (t \ right) $, yang hanya merupakan produk dari sinyal pembawa $ c \ left (t \ right) $ dan sinyal pesan $ m \ left (t \ right) $ ie ,

$$ s \ left (t \ right) = \ frac {4} {\ pi} \ sum_ {n = 1} ^ {\ infty} \ frac {\ left (-1 \ right) ^ {n-1}} {2n-1} \ cos \ kiri [2 \ pi f_ct \ kiri (2n-1 \ kanan) \ kanan] m \ kiri (t \ kanan) $$

Persamaan di atas mewakili gelombang DSBSC, yang diperoleh pada transformator keluaran modulator cincin.

Modulator DSBSC juga disebut sebagai product modulators karena mereka menghasilkan keluaran, yang merupakan produk dari dua sinyal masukan.

Proses mengekstraksi sinyal pesan asli dari gelombang DSBSC dikenal sebagai deteksi atau demodulasi DSBSC. Demodulator (detektor) berikut digunakan untuk mendemodulasi gelombang DSBSC.

• Detektor Koheren
• Costas Loop

Detektor Koheren

Di sini, sinyal pembawa yang sama (yang digunakan untuk menghasilkan sinyal DSBSC) digunakan untuk mendeteksi sinyal pesan. Oleh karena itu, proses deteksi ini disebut sebagaicoherent atau synchronous detection. Berikut adalah diagram blok dari detektor koheren.

Dalam proses ini, sinyal pesan dapat diekstraksi dari gelombang DSBSC dengan mengalikannya dengan pembawa, yang memiliki frekuensi dan fase pembawa yang sama yang digunakan dalam modulasi DSBSC. Sinyal yang dihasilkan kemudian dilewatkan melalui Low Pass Filter. Output dari filter ini adalah sinyal pesan yang diinginkan.

Biarkan gelombang DSBSC

$$ s \ kiri (t \ kanan) = A_c \ cos \ kiri (2 \ pi f_ct \ kanan) m \ kiri (t \ kanan) $$

Output dari osilator lokal adalah

$$ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + \ phi \ right) $$

Di mana, $ \ phi $ adalah perbedaan fase antara sinyal osilator lokal dan sinyal pembawa, yang digunakan untuk modulasi DSBSC.

Dari gambar tersebut, kita dapat menulis keluaran dari modulator produk sebagai

$$ v \ kiri (t \ kanan) = s \ kiri (t \ kanan) c \ kiri (t \ kanan) $$

Gantikan, nilai $ s \ left (t \ right) $ dan $ c \ left (t \ right) $ dalam persamaan di atas.

$$ \ Rightarrow v \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) m \ left (t \ right) A_c \ cos \ left (2 \ pi f_ct + \ phi \ right) $$

$ = {A_ {c}} ^ {2} \ cos \ left (2 \ pi f_ct \ right) \ cos \ left (2 \ pi f_ct + \ phi \ right) m \ kiri (t \ kanan) $

$ = \ frac {{A_ {c}} ^ {2}} {2} \ kiri [\ cos \ kiri (4 \ pi f_ct + \ phi \ right) + \ cos \ phi \ right] m \ kiri (t \ benar) $

$$ v \ left (t \ right) = \ frac {{A_ {c}} ^ {2}} {2} \ cos \ phi m \ left (t \ right) + \ frac {{A_ {c}} ^ {2}} {2} \ cos \ left (4 \ pi f_ct + \ phi \ right) m \ left (t \ right) $$

Dalam persamaan di atas, istilah pertama adalah versi berskala dari sinyal pesan. Itu dapat diekstraksi dengan melewatkan sinyal di atas melalui filter lolos rendah.

Oleh karena itu, keluaran dari low pass filter adalah

$$ v_0t = \ frac {{A_ {c}} ^ {2}} {2} \ cos \ phi m \ kiri (t \ kanan) $$

Amplitudo sinyal yang didemodulasi akan menjadi maksimum, jika $ \ phi = 0 ^ 0 $. Itu sebabnya sinyal osilator lokal dan sinyal pembawa harus dalam fase, yaitu, tidak boleh ada perbedaan fase antara kedua sinyal ini.

Amplitudo sinyal yang didemodulasi akan menjadi nol, jika $ \ phi = \ pm 90 ^ 0 $. Efek ini disebut sebagaiquadrature null effect.

Costas Loop

Loop costas digunakan untuk membuat sinyal pembawa (digunakan untuk modulasi DSBSC) dan sinyal yang dihasilkan secara lokal dalam fase. Berikut adalah diagram blok loop Costas.

Costas loopterdiri dari dua modulator produk dengan masukan umum $ s \ left (t \ right) $, yang merupakan gelombang DSBSC. Input lain untuk kedua modulator produk diambil dariVoltage Controlled Oscillator (VCO) dengan $ -90 ^ 0 $ pergeseran fasa ke salah satu modulator produk seperti yang ditunjukkan pada gambar.

Kita tahu bahwa persamaan gelombang DSBSC adalah

$$ s \ kiri (t \ kanan) = A_c \ cos \ kiri (2 \ pi f_ct \ kanan) m \ kiri (t \ kanan) $$

Biarkan output VCO menjadi

$$ c_1 \ kiri (t \ kanan) = \ cos \ kiri (2 \ pi f_ct + \ phi \ kanan) $$

Keluaran VCO ini diterapkan sebagai masukan pembawa modulator produk atas.

Oleh karena itu, keluaran dari modulator produk atas adalah

$$ v_1 \ kiri (t \ kanan) = s \ kiri (t \ kanan) c_1 \ kiri (t \ kanan) $$

Substitusi, nilai $ s \ left (t \ right) $ dan $ c_1 \ left (t \ right) $ dalam persamaan di atas.

$$ \ Rightarrow v_1 \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) m \ left (t \ right) \ cos \ left (2 \ pi f_ct + \ phi \ right) $ $

Setelah menyederhanakan, kita akan mendapatkan $ v_1 \ kiri (t \ kanan) $ as

$$ v_1 \ kiri (t \ kanan) = \ frac {A_c} {2} \ cos \ phi m \ kiri (t \ kanan) + \ frac {A_c} {2} \ cos \ kiri (4 \ pi f_ct + \ phi \ kanan) m \ kiri (t \ kanan) $$

Sinyal ini diterapkan sebagai masukan dari filter lintasan rendah atas. Output dari low pass filter ini adalah

$$ v_ {01} \ kiri (t \ kanan) = \ frac {A_c} {2} \ cos \ phi m \ kiri (t \ kanan) $$

Oleh karena itu, keluaran dari low pass filter ini adalah versi berskala dari sinyal modulasi.

Output dari $ -90 ^ 0 $ phase shifter adalah

$$ c_2 \ left (t \ right) = cos \ left (2 \ pi f_ct + \ phi-90 ^ 0 \ right) = \ sin \ left (2 \ pi f_ct + \ phi \ right) $$

Sinyal ini diterapkan sebagai masukan pembawa dari modulator produk yang lebih rendah.

Output dari modulator produk yang lebih rendah adalah

$$ v_2 \ kiri (t \ kanan) = s \ kiri (t \ kanan) c_2 \ kiri (t \ kanan) $$

Gantikan, nilai $ s \ left (t \ right) $ dan $ c_2 \ left (t \ right) $ dalam persamaan di atas.

$$ \ Rightarrow v_2 \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) m \ left (t \ right) \ sin \ left (2 \ pi f_ct + \ phi \ right) $ $

Setelah menyederhanakan, kita akan mendapatkan $ v_2 \ left (t \ right) $ as

$$ v_2 \ kiri (t \ kanan) = \ frac {A_c} {2} \ sin \ phi m \ kiri (t \ kanan) + \ frac {A_c} {2} \ sin \ kiri (4 \ pi f_ct + \ phi \ kanan) m \ kiri (t \ kanan) $$

Sinyal ini diterapkan sebagai masukan dari low pass filter. Output dari low pass filter ini adalah

$$ v_ {02} \ kiri (t \ kanan) = \ frac {A_c} {2} \ sin \ phi m \ kiri (t \ kanan) $$

Output dari filter lolos rendah ini memiliki perbedaan fase $ -90 ^ 0 $ dengan output filter akses rendah atas.

Keluaran dari dua filter lolos rendah ini diterapkan sebagai masukan dari pembeda fase. Berdasarkan perbedaan fasa antara kedua sinyal ini, pembeda fasa menghasilkan sinyal kontrol DC.

Sinyal ini diterapkan sebagai input VCO untuk memperbaiki kesalahan fase dalam output VCO. Oleh karena itu, sinyal pembawa (digunakan untuk modulasi DSBSC) dan sinyal yang dihasilkan secara lokal (keluaran VCO) berada dalam fase.

Pada bab sebelumnya, kita telah membahas modulasi dan demodulasi DSBSC. Sinyal termodulasi DSBSC memiliki dua sideband. Karena, dua sideband membawa informasi yang sama, tidak perlu mengirimkan kedua sideband. Kita bisa menghilangkan satu sideband.

Proses menekan salah satu sideband bersama dengan carrier dan mentransmisikan sideband tunggal disebut sebagai Single Sideband Suppressed Carrier sistem atau sederhana SSBSC. Itu diplot seperti yang ditunjukkan pada gambar berikut.

Pada gambar di atas, carrier dan sideband bawah ditekan. Karenanya, sideband atas digunakan untuk transmisi. Demikian pula, kita dapat menekan carrier dan sideband atas sambil mentransmisikan sideband bawah.

Sistem SSBSC ini, yang mentransmisikan sideband tunggal memiliki daya tinggi, karena daya yang dialokasikan untuk carrier dan sideband lainnya digunakan dalam mentransmisikan Single Sideband ini.

Ekspresi Matematika

Mari kita pertimbangkan ekspresi matematika yang sama untuk modulasi dan sinyal pembawa seperti yang telah kita bahas di bab-bab sebelumnya.

yaitu, Modulasi sinyal

$$ m \ kiri (t \ kanan) = A_m \ cos \ kiri (2 \ pi f_mt \ kanan) $$

Sinyal pembawa

$$ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $$

Secara matematis, kita dapat merepresentasikan persamaan gelombang SSBSC sebagai

$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] $ untuk sideband atas

Atau

$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] $ untuk sideband bawah

Bandwidth Gelombang SSBSC

Kita tahu bahwa gelombang termodulasi DSBSC berisi dua sideband dan bandwidth-nya $ 2f_m $. Karena gelombang termodulasi SSBSC hanya berisi satu pita sisi, bandwidth-nya adalah setengah dari bandwidth gelombang termodulasi DSBSC.

yaitu, Bandwidth of SSBSC modulated wave = $ \ frac {2f_m} {2} = f_m $

Oleh karena itu, bandwidth gelombang termodulasi SSBSC adalah $ f_m $ dan itu sama dengan frekuensi sinyal modulasi.

Perhitungan Daya Gelombang SSBSC

Perhatikan persamaan gelombang termodulasi SSBSC berikut ini.

$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] $ untuk sideband atas

Atau

$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] $ untuk sideband bawah

Kekuatan gelombang SSBSC sama dengan kekuatan salah satu komponen frekuensi pita samping.

$$ P_t = P_ {USB} = P_ {LSB} $$

Kita tahu bahwa rumus standar untuk kekuatan sinyal cos adalah

$$ P = \ frac {{v_ {rms}} ^ {2}} {R} = \ frac {\ left (v_m / \ sqrt {2} \ right) ^ 2} {R} $$

Dalam hal ini, kekuatan sideband atas adalah

$$ P_ {USB} = \ frac {\ kiri (A_m A_c / 2 \ sqrt {2} \ kanan) ^ 2} {R} = \ frac {{A_ {m}} ^ {2} {A_ {c} } ^ {2}} {8R} $$

Demikian pula, kita akan mendapatkan daya pita samping bawah yang sama dengan daya pita sisi atas.

$$ P_ {LSB} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8R} $$

Oleh karena itu, kekuatan gelombang SSBSC adalah

$$ P_t = P_ {USB} = P_ {LSB} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8R} $$

Keuntungan

• Bandwidth atau ruang spektrum yang ditempati lebih kecil dari gelombang AM dan DSBSC.

• Transmisi lebih banyak sinyal diperbolehkan.

• Daya disimpan.

• Sinyal daya tinggi dapat ditransmisikan.

• Jumlah kebisingan yang ada lebih sedikit.

• Pemudaran sinyal cenderung tidak terjadi.

Kekurangan

• Pembangkitan dan deteksi gelombang SSBSC adalah proses yang kompleks.

• Kualitas sinyal terpengaruh kecuali pemancar dan penerima SSB memiliki stabilitas frekuensi yang sangat baik.

Aplikasi

• Untuk persyaratan penghematan daya dan persyaratan bandwidth rendah.

• Dalam komunikasi bergerak darat, udara, dan maritim.

• Dalam komunikasi point-to-point.

• Dalam komunikasi radio.

• Di televisi, telemetri, dan komunikasi radar.

• Dalam komunikasi militer, seperti radio amatir, dll.

Pada bab ini, mari kita bahas tentang modulator yang menghasilkan gelombang SSBSC. Kita dapat menghasilkan gelombang SSBSC menggunakan dua metode berikut.

• Metode diskriminasi frekuensi
• Metode diskriminasi fase

Metode Diskriminasi Frekuensi

Gambar berikut menunjukkan diagram blok modulator SSBSC menggunakan metode diskriminasi frekuensi.

Dalam metode ini, pertama kita akan menghasilkan gelombang DSBSC dengan bantuan modulator produk. Kemudian, terapkan gelombang DSBSC ini sebagai masukan dari filter band pass. Band pass filter ini menghasilkan keluaran berupa gelombang SSBSC.

Pilih rentang frekuensi band pass filter sebagai spektrum gelombang SSBSC yang diinginkan. Ini berarti band pass filter dapat disetel ke frekuensi sideband atas atau frekuensi sideband bawah untuk mendapatkan gelombang SSBSC masing-masing yang memiliki sideband atas atau sideband bawah.

Metode Diskriminasi Fase

Gambar berikut menunjukkan diagram blok modulator SSBSC menggunakan metode diskriminasi fase.

Diagram blok ini terdiri dari dua modulator produk, dua pemindah fase $ -90 ^ 0 $, satu osilator lokal, dan satu blok musim panas. Modulator produk menghasilkan keluaran, yang merupakan produk dari dua masukan. Pengalih fase $ -90 ^ 0 $ menghasilkan keluaran, yang memiliki kelambatan fase $ -90 ^ 0 $ sehubungan dengan masukan tersebut.

Osilator lokal digunakan untuk menghasilkan sinyal pembawa. Blok musim panas menghasilkan keluaran, yang merupakan jumlah dari dua masukan atau selisih dua masukan berdasarkan polaritas masukan.

Sinyal modulasi $ A_m \ cos \ left (2 \ pi f_mt \ right) $ dan sinyal pembawa $ A_c \ cos \ left (2 \ pi f_ct \ right) $ langsung diterapkan sebagai input ke modulator produk atas. Jadi, modulator produk atas menghasilkan keluaran, yang merupakan produk dari kedua masukan tersebut.

Output dari modulator produk atas adalah

$$ s_1 \ kiri (t \ kanan) = A_mA_c \ cos \ kiri (2 \ pi f_mt \ kanan) \ cos \ kiri (2 \ pi f_ct \ kanan) $$

$$ \ Panah kanan s_1 \ kiri (t \ kanan) = \ frac {A_mA_c} {2} \ kiri \ {\ cos \ kiri [2 \ pi \ kiri (f_c + f_m \ kanan) t \ kanan] + \ cos \ kiri [2 \ pi \ kiri (f_c-f_m \ kanan) t \ kanan] \ kanan \} $$

Sinyal modulasi $ A_m \ cos \ left (2 \ pi f_mt \ right) $ dan sinyal pembawa $ A_c \ cos \ left (2 \ pi f_ct \ right) $ digeser fase sebesar $ -90 ^ 0 $ sebelum diterapkan sebagai masukan ke modulator produk yang lebih rendah. Jadi, modulator produk yang lebih rendah menghasilkan satu keluaran, yang merupakan produk dari kedua masukan tersebut.

Output dari modulator produk yang lebih rendah adalah

$$ s_2 \ kiri (t \ kanan) = A_mA_c \ cos \ kiri (2 \ pi f_mt-90 ^ 0 \ kanan) \ cos \ kiri (2 \ pi f_ct-90 ^ 0 \ kanan) $$

$ \ Rightarrow s_2 \ left (t \ right) = A_mA_c \ sin \ left (2 \ pi f_mt \ right) \ sin \ left (2 \ pi f_ct \ right) $

$ \ Rightarrow s_2 \ left (t \ right) = \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] - \ cos \ left [2 \ pi \ kiri (f_c + f_m \ kanan) t \ kanan] \ kanan \} $

Tambahkan $ s_1 \ kiri (t \ kanan) $ dan $ s_2 \ kiri (t \ kanan) $ untuk mendapatkan gelombang termodulasi SSBSC $ s \ left (t \ right) $ memiliki sideband bawah.

$ s \ kiri (t \ kanan) = \ frac {A_mA_c} {2} \ kiri \ {\ cos \ kiri [2 \ pi \ kiri (f_c + f_m \ kanan) t \ kanan] + \ cos \ kiri [2 \ pi \ kiri (f_c-f_m \ kanan) t \ kanan] \ kanan \} + $

$ \ frac {A_mA_c} {2} \ kiri \ {\ cos \ kiri [2 \ pi \ kiri (f_c-f_m \ kanan) t \ kanan] - \ cos \ kiri [2 \ pi \ kiri (f_c + f_m \ kanan) t \ kanan] \ kanan \} $

$ \ Panah kanan s \ kiri (t \ kanan) = A_mA_c \ cos \ kiri [2 \ pi \ kiri (f_c-f_m \ kanan) t \ kanan] $

Kurangi $ s_2 \ left (t \ right) $ dari $ s_1 \ left (t \ right) $ untuk mendapatkan gelombang termodulasi SSBSC $ s \ left (t \ right) $ dengan sideband atas.

$ s \ kiri (t \ kanan) = \ frac {A_mA_c} {2} \ kiri \ {\ cos \ kiri [2 \ pi \ kiri (f_c + f_m \ kanan) t \ kanan] + \ cos \ kiri [2 \ pi \ kiri (f_c-f_m \ kanan) t \ kanan] \ kanan \} - $

$ \ frac {A_mA_c} {2} \ kiri \ {\ cos \ kiri [2 \ pi \ kiri (f_c-f_m \ kanan) t \ kanan] - \ cos \ kiri [2 \ pi \ kiri (f_c + f_m \ kanan) t \ kanan] \ kanan \} $

$ \ Panah kanan s \ kiri (t \ kanan) = A_mA_c \ cos \ kiri [2 \ pi \ kiri (f_c + f_m \ kanan) t \ kanan] $

Oleh karena itu, dengan memilih polaritas input pada blok musim panas, kita akan mendapatkan gelombang SSBSC yang memiliki sideband atas atau sideband bawah.

Proses mengekstraksi sinyal pesan asli dari gelombang SSBSC dikenal sebagai deteksi atau demodulasi SSBSC. Detektor koheren digunakan untuk mendemodulasi gelombang SSBSC.

Detektor Koheren

Di sini, sinyal pembawa yang sama (yang digunakan untuk menghasilkan gelombang SSBSC) digunakan untuk mendeteksi sinyal pesan. Oleh karena itu, proses deteksi ini disebut sebagaicoherent atau synchronous detection. Berikut adalah diagram blok dari detektor koheren.

Dalam proses ini, sinyal pesan dapat diekstraksi dari gelombang SSBSC dengan mengalikannya dengan pembawa, yang memiliki frekuensi dan fase pembawa yang sama yang digunakan dalam modulasi SSBSC. Sinyal yang dihasilkan kemudian dilewatkan melalui Low Pass Filter. Output dari filter ini adalah sinyal pesan yang diinginkan.

Simak berikut ini SSBSC gelombang memiliki lower sideband.

$$ s \ kiri (t \ kanan) = \ frac {A_mA_c} {2} \ cos \ kiri [2 \ pi \ kiri (f_c-f_m \ kanan) t \ kanan] $$

Output dari osilator lokal adalah

$$ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $$

Dari gambar tersebut, kita dapat menulis keluaran dari modulator produk sebagai

$$ v \ kiri (t \ kanan) = s \ kiri (t \ kanan) c \ kiri (t \ kanan) $$

Gantikan nilai $ s \ left (t \ right) $ dan $ c \ left (t \ right) $ dalam persamaan di atas.

$$ v \ kiri (t \ kanan) = \ frac {A_mA_c} {2} \ cos \ kiri [2 \ pi \ kiri (f_c-f_m \ kanan) t \ kanan] A_c \ cos \ kiri (2 \ pi f_ct \ benar) $$

$ = \ frac {A_m {A_ {c}} ^ {2}} {2} \ cos \ kiri [2 \ pi \ kiri (f_c -f_m \ kanan) t \ kanan] \ cos \ kiri (2 \ pi f_ct \ benar) $

$ = \ frac {A_m {A_ {c}} ^ {2}} {4} \ kiri \ {\ cos \ kiri [2 \ pi \ kiri (2f_c-fm \ kanan) \ kanan] + \ cos \ kiri ( 2 \ pi f_m \ kanan) t \ kanan \} $

$ v \ kiri (t \ kanan) = \ frac {A_m {A_ {c}} ^ {2}} {4} \ cos \ left (2 \ pi f_mt \ kanan) + \ frac {A_m {A_ {c} } ^ {2}} {4} \ cos \ kiri [2 \ pi \ kiri (2f_c-f_m \ kanan) t \ kanan] $

Dalam persamaan di atas, istilah pertama adalah versi berskala dari sinyal pesan. Itu dapat diekstraksi dengan melewatkan sinyal di atas melalui filter lolos rendah.

Oleh karena itu, keluaran dari low pass filter adalah

$$ v_0 \ kiri (t \ kanan) = \ frac {A_m {A_ {c}} ^ {2}} {4} \ cos \ kiri (2 \ pi f_mt \ kanan) $$

Di sini, faktor penskalaannya adalah $ \ frac {{A_ {c}} ^ {2}} {4} $.

Kita dapat menggunakan diagram blok yang sama untuk mendemodulasi gelombang SSBSC yang memiliki pita sisi atas. Simak berikut iniSSBSC gelombang memiliki upper sideband.

$$ s \ kiri (t \ kanan) = \ frac {A_mA_c} {2} \ cos \ kiri [2 \ pi \ kiri (f_c + f_m \ kanan) t \ kanan] $$

Output dari osilator lokal adalah

$$ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $$

Kita dapat menulis keluaran dari modulator produk sebagai

$$ v \ kiri (t \ kanan) = s \ kiri (t \ kanan) c \ kiri (t \ kanan) $$

Gantikan nilai $ s \ left (t \ right) $ dan $ c \ left (t \ right) $ dalam persamaan di atas.

$$ \ Rightarrow v \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] A_c \ cos \ left (2 \ pi f_ct \ kanan) $$

$ = \ frac {A_m {A_ {c}} ^ {2}} {2} \ cos \ kiri [2 \ pi \ kiri (f_c + f_m \ kanan) t \ kanan] \ cos \ kiri (2 \ pi f_ct \ benar) $

$ = \ frac {A_m {A_ {c}} ^ {2}} {4} \ kiri \ {\ cos \ kiri [2 \ pi \ kiri (2f_c + f_m \ kanan) t \ kanan] + \ cos \ kiri (2 \ pi f_mt \ kanan) \ kanan \} $

$ v \ kiri (t \ kanan) = \ frac {A_m {A_ {c}} ^ {2}} {4} \ cos \ left (2 \ pi f_mt \ kanan) + \ frac {A_m {A_ {c} } ^ {2}} {4} \ cos \ kiri [2 \ pi \ kiri (2f_c + f_m \ kanan) t \ kanan] $

Dalam persamaan di atas, istilah pertama adalah versi berskala dari sinyal pesan. Itu dapat diekstraksi dengan melewatkan sinyal di atas melalui filter lolos rendah.

Oleh karena itu, keluaran dari low pass filter adalah

$$ v_0 \ kiri (t \ kanan) = \ frac {A_m {A_ {c}} ^ {2}} {4} \ cos \ kiri (2 \ pi f_mt \ kanan) $$

Di sini juga faktor penskalaannya adalah $ \ frac {{A_ {c}} ^ {2}} {4} $.

Oleh karena itu, kami mendapatkan keluaran yang didemodulasi sama dalam kedua kasus dengan menggunakan detektor koheren.

Pada bab sebelumnya, kita telah membahas modulasi dan demodulasi SSBSC. Sinyal termodulasi SSBSC hanya memiliki satu frekuensi sideband. Secara teoritis, kita bisa mendapatkan satu komponen frekuensi sideband secara lengkap dengan menggunakan band pass filter yang ideal. Namun, secara praktis kita mungkin tidak mendapatkan seluruh komponen frekuensi sideband. Karena ini, beberapa informasi hilang.

Untuk menghindari kerugian ini, suatu teknik dipilih, yaitu kompromi antara DSBSC dan SSBSC. Teknik ini dikenal sebagaiVestigial Side Band Suppressed Carrier (VSBSC)teknik. Kata "sisa" berarti "bagian" dari mana, nama itu berasal.

VSBSC Modulationadalah proses, di mana bagian dari sinyal yang disebut vestige dimodulasi bersama dengan satu sideband. Spektrum frekuensi gelombang VSBSC ditunjukkan pada gambar berikut.

Bersama dengan sideband atas, bagian dari sideband bawah juga sedang ditransmisikan dalam teknik ini. Demikian pula, kita dapat mengirimkan sideband bawah bersama dengan bagian sideband atas. Pita pelindung dengan lebar yang sangat kecil dipasang di kedua sisi VSB untuk menghindari gangguan. Modulasi VSB banyak digunakan dalam transmisi televisi.

Bandwidth Modulasi VSBSC

Kita tahu bahwa bandwidth gelombang termodulasi SSBSC adalah $ f_m $. Karena gelombang termodulasi VSBSC berisi komponen frekuensi dari satu pita sisi bersama dengan sisa pita sisi lain, bandwidth itu akan menjadi jumlah bandwidth gelombang termodulasi SSBSC dan frekuensi sisa $ f_v $.

i.e., Bandwidth of VSBSC Modulated Wave = $f_m + f_v$

Keuntungan

Berikut adalah keuntungan dari modulasi VSBSC.

• Sangat efisien.

• Pengurangan bandwidth jika dibandingkan dengan gelombang AM dan DSBSC.

• Desain filter itu mudah, karena tidak memerlukan akurasi tinggi.

• Transmisi komponen frekuensi rendah dimungkinkan, tanpa kesulitan apa pun.

• Memiliki karakteristik fase yang baik.

Kekurangan

Berikut adalah kerugian dari modulasi VSBSC.

• Bandwidth lebih banyak jika dibandingkan dengan gelombang SSBSC.

• Demodulasi itu rumit.

Aplikasi

Aplikasi VSBSC yang paling menonjol dan standar adalah untuk transmisi sinyal televisi. Selain itu, ini adalah teknik yang paling nyaman dan efisien jika penggunaan bandwidth dipertimbangkan.

Sekarang, mari kita bahas tentang modulator yang menghasilkan gelombang VSBSC dan demodulator yang mendemodulasi gelombang VSBSC satu per satu.

Generasi VSBSC

Pembangkitan gelombang VSBSC mirip dengan pembangkitan gelombang SSBSC. Modulator VSBSC ditunjukkan pada gambar berikut.

Dalam metode ini, pertama kita akan menghasilkan gelombang DSBSC dengan bantuan modulator produk. Kemudian, terapkan gelombang DSBSC ini sebagai masukan dari filter pembentuk sideband. Filter ini menghasilkan keluaran berupa gelombang VSBSC.

Sinyal modulasi $ m \ left (t \ right) $ dan sinyal carrier $ A_c \ cos \ left (2 \ pi f_ct \ right) $ diterapkan sebagai input ke modulator produk. Oleh karena itu, modulator produk menghasilkan keluaran, yang merupakan produk dari kedua masukan tersebut.

Oleh karena itu, keluaran dari modulator produk adalah

$$ p \ kiri (t \ kanan) = A_c \ cos \ kiri (2 \ pi f_ct \ kanan) m \ kiri (t \ kanan) $$

Terapkan transformasi Fourier di kedua sisi

$$ P \ kiri (f \ kanan) = \ frac {A_c} {2} \ kiri [M \ kiri (f-f_c \ kanan) + M \ kiri (f + f_c \ kanan) \ kanan] $$

Persamaan di atas merupakan persamaan spektrum frekuensi DSBSC.

Biarkan fungsi transfer dari filter pembentuk sideband menjadi $ H \ left (f \ right) $. Filter ini memiliki input $ p \ left (t \ right) $ dan outputnya adalah gelombang termodulasi VSBSC $ s \ left (t \ right) $. Transformasi Fourier dari $ p \ left (t \ right) $ dan $ s \ left (t \ right) $ masing-masing adalah $ P \ left (t \ right) $ dan $ S \ left (t \ right) $.

Secara matematis, kita dapat menulis $ S \ left (f \ right) $ as

$$ S \ kiri (t \ kanan) = P \ kiri (f \ kanan) H \ kiri (f \ kanan) $$

Gantikan nilai $ P \ left (f \ right) $ dalam persamaan di atas.

$$ S \ kiri (f \ kanan) = \ frac {A_c} {2} \ kiri [M \ kiri (f-f_c \ kanan) + M \ kiri (f + f_c \ kanan) \ kanan] H \ kiri ( f \ benar) $$

Persamaan di atas merupakan persamaan spektrum frekuensi VSBSC.

Demodulasi VSBSC

Demodulasi gelombang VSBSC mirip dengan demodulasi gelombang SSBSC. Di sini, sinyal pembawa yang sama (yang digunakan untuk menghasilkan gelombang VSBSC) digunakan untuk mendeteksi sinyal pesan. Oleh karena itu, proses deteksi ini disebut sebagaicoherent atau synchronous detection. Demodulator VSBSC ditunjukkan pada gambar berikut.

Dalam proses ini, sinyal pesan dapat diekstraksi dari gelombang VSBSC dengan cara mengalikannya dengan carrier yang memiliki frekuensi yang sama dan fase carrier yang digunakan dalam modulasi VSBSC. Sinyal yang dihasilkan kemudian dilewatkan melalui Low Pass Filter. Output dari filter ini adalah sinyal pesan yang diinginkan.

Misalkan gelombang VSBSC menjadi $ s \ left (t \ right) $ dan sinyal pembawa $ A_c \ cos \ left (2 \ pi f_ct \ right) $.

Dari gambar tersebut, kita dapat menulis keluaran dari modulator produk sebagai

$$ v \ kiri (t \ kanan) = A_c \ cos \ kiri (2 \ pi f_ct \ kanan) s \ kiri (t \ kanan) $$

Terapkan transformasi Fourier di kedua sisi

$$ V \ kiri (f \ kanan) = \ frac {A_c} {2} \ kiri [S \ kiri (f-f_c \ kanan) + S \ kiri (f + f_c \ kanan) \ kanan] $$

Kita tahu bahwa $ S \ kiri (f \ kanan) = \ frac {A_c} {2} \ kiri [M \ kiri (f-f_c \ kanan) + M \ kiri (f + f_c \ kanan) \ kanan] H \ kiri (f \ kanan) $

Dari persamaan di atas, mari kita cari $ S \ left (f-f_c \ right) $ dan $ S \ left (f + f_c \ right) $.

$$ S \ kiri (f-f_c \ kanan) = \ frac {A_c} {2} \ kiri [M \ kiri (f-f_c-f_c \ kanan) + M \ kiri (f-f_c + f_c \ kanan) \ kanan] H \ kiri (f-f_c \ kanan) $$

$ \ Kananarrow S \ kiri (f-f_c \ kanan) = \ frac {A_c} {2} \ kiri [M \ kiri (f-2f_c \ kanan) + M \ kiri (f \ kanan) \ kanan] H \ kiri (f-f_c \ kanan) $

$$ S \ kiri (f + f_c \ kanan) = \ frac {A_c} {2} \ kiri [M \ kiri (f + f_c-f_c \ kanan) + M \ kiri (f + f_c + f_c \ kanan) \ kanan] H \ kiri (f + f_c \ kanan) $$

$ \ Kananarrow S \ kiri (f + f_c \ kanan) = \ frac {A_c} {2} \ kiri [M \ kiri (f \ kanan) + M \ kiri (f + 2f_c \ kanan) \ kanan] H \ kiri (f + f_c \ kanan) $

Gantikan, $ S \ left (f-f_c \ right) $ dan $ S \ left (f + f_c \ right) $ nilai dalam $ V \ left (f \ right) $.

$ V (f) = \ frac {A_c} {2} [\ frac {A_c} {2} [M (f-2f_c) + M (f)] H (f-f_c) + $

$ \ frac {A_c} {2} [M (f) + M (f + 2f_c)] H (f + f_c)] $

$ \ Kananarrow V \ kiri (f \ kanan) = \ frac {{A_ {c}} ^ {2}} {4} M \ kiri (f \ kanan) \ kiri [H \ kiri (f-f_c \ kanan) + H \ kiri (f + f_c \ kanan) \ kanan] $

$ + \ frac {{A_ {c}} ^ {2}} {4} \ kiri [M \ kiri (f-2f_c \ kanan) H \ kiri (f-f_c \ kanan) + M \ kiri (f + 2f_c \ kanan) H \ kiri (f + f_c \ kanan) \ kanan] $

Dalam persamaan di atas, istilah pertama mewakili versi berskala dari spektrum frekuensi sinyal pesan yang diinginkan. Itu dapat diekstraksi dengan melewatkan sinyal di atas melalui filter lolos rendah.

$$ V_0 \ kiri (f \ kanan) = \ frac {{A_ {c}} ^ {2}} {4} M \ kiri (f \ kanan) \ kiri [H \ kiri (f-f_c \ kanan) + H \ kiri (f + f_c \ kanan) \ kanan] $$

Jenis modulasi lain dalam modulasi gelombang kontinu adalah Angle Modulation. Modulasi Sudut adalah proses di mana frekuensi atau fase sinyal pembawa bervariasi sesuai dengan sinyal pesan.

Persamaan standar gelombang termodulasi sudut adalah

$$ s \ kiri (t \ kanan) = A_c \ cos \ theta _i \ kiri (t \ kanan) $$

Dimana,

$ A_c $ adalah amplitudo gelombang termodulasi, yang sama dengan amplitudo sinyal pembawa

$ \ theta _i \ left (t \ right) $ adalah sudut gelombang termodulasi

Modulasi sudut selanjutnya dibagi menjadi modulasi frekuensi dan modulasi fase.

• Frequency Modulation adalah proses memvariasikan frekuensi sinyal pembawa secara linier dengan sinyal pesan.

• Phase Modulation adalah proses memvariasikan fase sinyal pembawa secara linier dengan sinyal pesan.

Sekarang, mari kita bahas secara rinci.

Modulasi frekuensi

Dalam modulasi amplitudo, amplitudo sinyal pembawa bervariasi. Padahal, dalamFrequency Modulation (FM), frekuensi sinyal pembawa bervariasi sesuai dengan amplitudo sesaat dari sinyal modulasi.

Oleh karena itu, dalam modulasi frekuensi, amplitudo dan fase sinyal pembawa tetap konstan. Ini bisa lebih dipahami dengan mengamati gambar-gambar berikut.

Frekuensi gelombang termodulasi meningkat, ketika amplitudo sinyal modulasi atau pesan meningkat. Demikian pula, frekuensi gelombang termodulasi menurun, ketika amplitudo sinyal modulasi menurun. Perhatikan bahwa, frekuensi gelombang termodulasi tetap konstan dan itu sama dengan frekuensi sinyal pembawa, ketika amplitudo sinyal modulasi adalah nol.

Representasi Matematika

Persamaan untuk frekuensi sesaat $ f_i $ dalam modulasi FM adalah

$$ f_i = f_c + k_fm \ kiri (t \ kanan) $$

Dimana,

$ f_c $ adalah frekuensi pembawa

$ k_t $ adalah sensitivitas frekuensi

$ m \ left (t \ right) $ adalah sinyal pesan

Kita mengetahui hubungan antara frekuensi sudut $ \ omega_i $ dan sudut $ \ theta _i \ left (t \ right) $ as

$$ \ omega_i = \ frac {d \ theta _i \ kiri (t \ kanan)} {dt} $$

$ \ Rightarrow 2 \ pi f_i = \ frac {d \ theta _i \ left (t \ kanan)} {dt} $

$ \ Rightarrow \ theta _i \ left (t \ right) = 2 \ pi \ int f_i dt $

Gantikan, $ f_i $ nilai dalam persamaan di atas.

$$ \ theta _i \ kiri (t \ kanan) = 2 \ pi \ int \ kiri (f_c + k_f m \ kiri (t \ kanan) \ kanan) dt $$

$ \ Rightarrow \ theta _i \ left (t \ right) = 2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ kanan) dt $

Gantikan, $ \ theta _i \ left (t \ right) $ nilai dalam persamaan standar gelombang termodulasi sudut.

$$ s \ kiri (t \ kanan) = A_c \ cos \ kiri (2 \ pi f_ct + 2 \ pi k_f \ int m \ kiri (t \ kanan) dt \ kanan) $$

Ini adalah equation of FM wave.

Jika sinyal modulasi adalah $ m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right) $, maka persamaan gelombang FM menjadi

$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + \ beta \ sin \ left (2 \ pi f_mt \ right) \ kanan) $$

Dimana,

$ \ beta $ = modulation index $ = \ frac {\ Delta f} {f_m} = \ frac {k_fA_m} {f_m} $

Perbedaan antara frekuensi termodulasi FM (frekuensi sesaat) dan frekuensi pembawa normal disebut sebagai Frequency Deviation. Ini dilambangkan dengan $ \ Delta f $, yang sama dengan hasil kali $ k_f $ dan $ A_m $.

FM dapat dibagi menjadi Narrowband FM dan Wideband FM berdasarkan nilai indeks modulasi $ \ beta $.

Narrowband FM

Berikut adalah fitur-fitur dari Narrowband FM.

• Modulasi frekuensi ini memiliki bandwidth yang kecil jika dibandingkan dengan pita lebar FM.

• Indeks modulasi $ \ beta $ kecil, yaitu kurang dari 1.

• Spektrumnya terdiri dari carrier, sideband atas dan sideband bawah.

• Ini digunakan dalam komunikasi seluler seperti nirkabel polisi, ambulans, taksi, dll.

Wideband FM

Berikut adalah fitur-fitur Wideband FM.

• Modulasi frekuensi ini memiliki bandwidth tak terbatas.

• Indeks modulasi $ \ beta $ besar, yaitu lebih tinggi dari 1.

• Spektrumnya terdiri dari pembawa dan sideband dalam jumlah tak terbatas, yang terletak di sekitarnya.

• Ini digunakan dalam hiburan, aplikasi penyiaran seperti radio FM, TV, dll.

Modulasi Fase

Dalam modulasi frekuensi, frekuensi pembawa bervariasi. Padahal, dalamPhase Modulation (PM), fase sinyal pembawa bervariasi sesuai dengan amplitudo sesaat dari sinyal modulasi.

Jadi, dalam modulasi fase, amplitudo dan frekuensi sinyal pembawa tetap konstan. Ini bisa lebih dipahami dengan mengamati gambar-gambar berikut.

Fase gelombang termodulasi memiliki titik tak terhingga, dimana pergeseran fasa dalam gelombang dapat terjadi. Amplitudo sesaat dari sinyal modulasi mengubah fase sinyal pembawa. Ketika amplitudo positif, fase berubah ke satu arah dan jika amplitudo negatif, fase berubah ke arah yang berlawanan.

Mathematical Representation

The equation for instantaneous phase $\phi_i$ in phase modulation is

$$\phi _i=k_p m\left ( t \right )$$

Where,

• $k_p$ is the phase sensitivity

• $m\left ( t \right )$ is the message signal

The standard equation of angle modulated wave is

$$s\left ( t \right )=A_c \cos \left ( 2 \pi f_ct+\phi_i \right )$$

Substitute, $\phi_i$ value in the above equation.

$$s\left ( t \right )=A_c \cos \left ( 2 \pi f_ct+k_p m \left ( t \right )\right )$$

This is the equation of PM wave.

If the modulating signal, $m\left ( t \right )=A_m \cos \left ( 2 \pi f_mt \right ) $, then the equation of PM wave will be

$$s\left ( t \right )=A_c \cos\left (2 \pi f_ct+\beta \cos\left ( 2 \pi f_mt \right ) \right )$$

Where,

• $\beta$ = modulation index = $\Delta \phi=k_pA_m$

• $\Delta \phi$ is phase deviation

Phase modulation is used in mobile communication systems, while frequency modulation is used mainly for FM broadcasting.

In the previous chapter, we have discussed the parameters used in Angle modulation. Each parameter has its own formula. By using those formulas, we can find the respective parameter values. In this chapter, let us solve a few problems based on the concept of Frequency Modulation.

Problem 1

A sinusoidal modulating waveform of amplitude 5 V and a frequency of 2 KHz is applied to FM generator, which has a frequency sensitivity of 40 Hz/volt. Calculate the frequency deviation, modulation index, and bandwidth.

Solution

Given, the amplitude of modulating signal, $A_m=5V$

Frequency of modulating signal, $f_m=2 KHz$

Frequency sensitivity, $k_f=40 Hz/volt$

We know the formula for Frequency deviation as

$$\Delta f=k_f A_m$$

Substitute $k_f$ and $A_m$ values in the above formula.

$$\Delta f=40 \times 5=200Hz$$

Therefore, frequency deviation, $\Delta f$ is $200Hz$

The formula for modulation index is

$$\beta = \frac{\Delta f}{f_m}$$

Substitute $\Delta f$ and $f_m$ values in the above formula.

$$\beta=\frac{200}{2 \times 1000}=0.1$$

Here, the value of modulation index, $\beta$ is 0.1, which is less than one. Hence, it is Narrow Band FM.

The formula for Bandwidth of Narrow Band FM is the same as that of AM wave.

$$BW=2f_m$$

Substitute $f_m$ value in the above formula.

$$BW=2 \times 2K=4KHz$$

Therefore, the bandwidth of Narrow Band FM wave is $4 KHz$.

Problem 2

An FM wave is given by $s\left ( t \right )=20 \cos\left ( 8 \pi \times10^6t+9 \sin\left ( 2 \pi \times 10^3 t \right ) \right )$. Calculate the frequency deviation, bandwidth, and power of FM wave.

Solution

Given, the equation of an FM wave as

$$s\left ( t \right )=20 \cos\left ( 8 \pi \times10^6t+9 \sin\left ( 2 \pi \times 10^3 t \right ) \right )$$

We know the standard equation of an FM wave as

$$s\left ( t \right )=A_c \cos\left ( 2 \pi f_ct + \beta \sin \left ( 2 \pi f_mt \right ) \right )$$

We will get the following values by comparing the above two equations.

Amplitude of the carrier signal, $A_c=20V$

Frequency of the carrier signal, $f_c=4 \times 10^6 Hz=4 MHz$

Frequency of the message signal, $f_m=1 \times 10^3 Hz = 1KHz$

Modulation index, $\beta=9$

Here, the value of modulation index is greater than one. Hence, it is Wide Band FM.

We know the formula for modulation index as

$$\beta=\frac {\Delta f}{f_m}$$

Rearrange the above equation as follows.

$$\Delta=\beta f_m$$

Substitute $\beta$ and $f_m$ values in the above equation.

$$\Delta=9 \times 1K =9 KHz$$

Therefore, frequency deviation, $\Delta f$ is $9 KHz$.

The formula for Bandwidth of Wide Band FM wave is

$$BW=2\left ( \beta +1 \right )f_m$$

Substitute $\beta$ and $f_m$ values in the above formula.

$$BW=2\left ( 9 +1 \right )1K=20KHz$$

Therefore, the bandwidth of Wide Band FM wave is $20 KHz$

Formula for power of FM wave is

$$P_c= \frac{{A_{c}}^{2}}{2R}$$

Assume, $R=1\Omega$ and substitute $A_c$ value in the above equation.

$$P=\frac{\left ( 20 \right )^2}{2\left ( 1 \right )}=200W$$

Therefore, the power of FM wave is $200$ watts.

In this chapter, let us discuss about the modulators which generate NBFM and WBFM waves. First, let us discuss about the generation of NBFM.

Generation of NBFM

We know that the standard equation of FM wave is

$$s\left ( t \right )=A_c \cos\left ( 2 \pi f_ct+2 \pi k_f\int m\left ( t \right ) dt\right )$$

$\Rightarrow s\left ( t \right )=A_c \cos\left ( 2 \pi f_ct \right ) \cos\left ( 2 \pi k_f\int m\left ( t \right )dt \right )-$

$A_c \sin\left ( 2 \pi f_ct \right ) \sin\left ( 2 \pi k_f\int m\left ( t \right )dt \right )$

For NBFM,

$$\left | 2 \pi k_f\int m\left ( t \right )dt \right | < < 1$$

We know that $\cos \theta \approx 1$ and $\sin \theta \approx 1$ when $\theta$ is very small.

By using the above relations, we will get the NBFM equation as

$$s\left ( t \right )=A_c \cos\left ( 2 \pi f_ct \right )-A_c \sin\left ( 2 \pi f_ct \right )2 \pi k_f\int m\left ( t \right )dt$$

The block diagram of NBFM modulator is shown in the following figure.

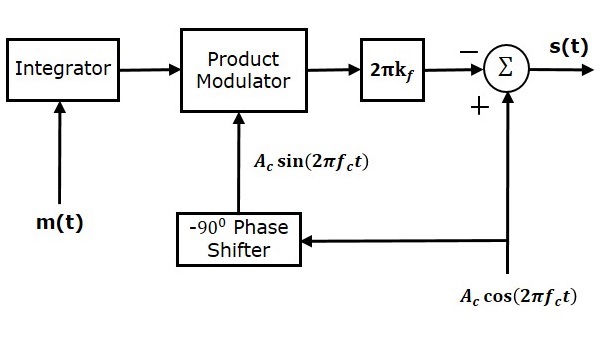
Here, the integrator is used to integrate the modulating signal $m\left (t \right )$. The carrier signal $A_c \cos \left ( 2 \pi f_ct \right )$ is the phase shifted by $-90^0$ to get $A_c \sin \left ( 2 \pi f_ct \right )$ with the help of $-90^0$ phase shifter. The product modulator has two inputs $\int m\left ( t \right )dt$ and $A_c \sin \left ( 2 \pi f_ct \right )$. It produces an output, which is the product of these two inputs.

This is further multiplied with $2 \pi k_f$ by placing a block $2 \pi k_f$ in the forward path. The summer block has two inputs, which are nothing but the two terms of NBFM equation. Positive and negative signs are assigned for the carrier signal and the other term at the input of the summer block. Finally, the summer block produces NBFM wave.

Generation of WBFM

The following two methods generate WBFM wave.

• Direct method
• Indirect method

Direct Method

This method is called as the Direct Method because we are generating a wide band FM wave directly. In this method, Voltage Controlled Oscillator (VCO) is used to generate WBFM. VCO produces an output signal, whose frequency is proportional to the input signal voltage. This is similar to the definition of FM wave. The block diagram of the generation of WBFM wave is shown in the following figure.

Here, the modulating signal $m\left (t \right )$ is applied as an input of Voltage Controlled Oscillator (VCO). VCO produces an output, which is nothing but the WBFM.

$$f_i \: \alpha \: m\left ( t \right )$$

$$\Rightarrow f_i=f_c+k_fm\left ( t \right )$$

Where,

$f_i$ is the instantaneous frequency of WBFM wave.

Indirect Method

This method is called as Indirect Method because we are generating a wide band FM wave indirectly. This means, first we will generate NBFM wave and then with the help of frequency multipliers we will get WBFM wave. The block diagram of generation of WBFM wave is shown in the following figure.

This block diagram contains mainly two stages. In the first stage, the NBFM wave will be generated using NBFM modulator. We have seen the block diagram of NBFM modulator at the beginning of this chapter. We know that the modulation index of NBFM wave is less than one. Hence, in order to get the required modulation index (greater than one) of FM wave, choose the frequency multiplier value properly.

Frequency multiplier is a non-linear device, which produces an output signal whose frequency is ‘n’ times the input signal frequency. Where, ‘n’ is the multiplication factor.

If NBFM wave whose modulation index $\beta$ is less than 1 is applied as the input of frequency multiplier, then the frequency multiplier produces an output signal, whose modulation index is ‘n’ times $\beta$ and the frequency also ‘n’ times the frequency of WBFM wave.

Sometimes, we may require multiple stages of frequency multiplier and mixers in order to increase the frequency deviation and modulation index of FM wave.

In this chapter, let us discuss about the demodulators which demodulate the FM wave. The following two methods demodulate FM wave.

• Frequency discrimination method
• Phase discrimination method

Frequency Discrimination Method

We know that the equation of FM wave is

$$s\left ( t \right ) =A_c \cos \left ( 2 \pi f_ct+2 \pi k_f \int m\left ( t \right )dt \right )$$

Differentiate the above equation with respect to 't'.

$$\frac{ds\left ( t \right )}{dt}= -A_c\left ( 2 \pi f_c+2 \pi k_fm\left ( t \right ) \right ) \sin\left ( 2 \pi f_ct+2 \pi k_f\int m\left ( t \right )dt \right )$$

We can write, $-\sin \theta$ as $\sin \left ( \theta -180^0 \right )$.

$$\Rightarrow \frac{ds(t)}{dt}=A_c\left ( 2 \pi f_c+2 \pi k_fm\left ( t \right ) \right )\sin\left ( 2 \pi f_ct+2 \pi k_f \int m\left ( t \right )dt-180^0 \right )$$

$$\Rightarrow \frac{ds(t)}{dt}=A_c\left ( 2 \pi f_c \right )\left [ 1+\left ( \frac{k_f}{k_c} \right )m\left ( t \right ) \right ] \sin\left ( 2 \pi f_ct+2 \pi k_f\int m\left ( t \right )dt-180^0 \right )$$

In the above equation, the amplitude term resembles the envelope of AM wave and the angle term resembles the angle of FM wave. Here, our requirement is the modulating signal $m\left ( t \right )$. Hence, we can recover it from the envelope of AM wave.

The following figure shows the block diagram of FM demodulator using frequency discrimination method.

This block diagram consists of the differentiator and the envelope detector. Differentiator is used to convert the FM wave into a combination of AM wave and FM wave. This means, it converts the frequency variations of FM wave into the corresponding voltage (amplitude) variations of AM wave. We know the operation of the envelope detector. It produces the demodulated output of AM wave, which is nothing but the modulating signal.

Phase Discrimination Method

The following figure shows the block diagram of FM demodulator using phase discrimination method.

This block diagram consists of the multiplier, the low pass filter, and the Voltage Controlled Oscillator (VCO). VCO produces an output signal $v \left ( t \right )$, whose frequency is proportional to the input signal voltage $d \left ( t \right )$. Initially, when the signal $d \left ( t \right )$ is zero, adjust the VCO to produce an output signal $v \left ( t \right )$, having a carrier frequency and $-90^0$ phase shift with respect to the carrier signal.

FM wave $s \left ( t \right )$ and the VCO output $v \left ( t \right )$ are applied as inputs of the multiplier. The multiplier produces an output, having a high frequency component and a low frequency component. Low pass filter eliminates the high frequency component and produces only the low frequency component as its output.

This low frequency component contains only the term-related phase difference. Hence, we get the modulating signal $m \left ( t \right )$ from this output of the low pass filter.

Multiplexing is the process of combining multiple signals into one signal, over a shared medium. If the analog signals are multiplexed, then it is called as analog multiplexing. Similarly, if the digital signals are multiplexed, then it is called as digital multiplexing.

Multiplexing was first developed in telephony. A number of signals were combined to send through a single cable. The process of multiplexing divides a communication channel into several number of logical channels, allotting each one for a different message signal or a data stream to be transferred. The device that does multiplexing can be called as Multiplexer or MUX.

The reverse process, i.e., extracting the number of channels from one, which is done at the receiver is called as de-multiplexing. The device that does de-multiplexing can be called as de-multiplexer or DEMUX.

The following figures illustrates the concept of MUX and DEMUX. Their primary use is in the field of communications.

Types of Multiplexers

There are mainly two types of multiplexers, namely analog and digital. They are further divided into Frequency Division Multiplexing (FDM), Wavelength Division Multiplexing (WDM), and Time Division Multiplexing (TDM). The following figure gives a detailed idea about this classification.

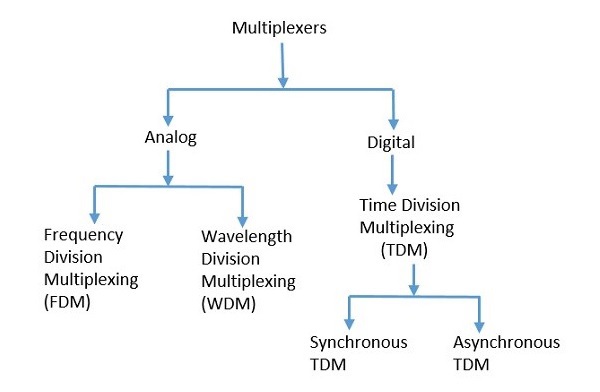
There are many types of multiplexing techniques. Out of which, we have the main types with general classification, mentioned in the above figure. Let us take a look at them individually.

Analog Multiplexing

The signals used in analog multiplexing techniques are analog in nature. The analog signals are multiplexed according to their frequency (FDM) or wavelength (WDM).

Frequency Division Multiplexing

In analog multiplexing, the most used technique is Frequency Division Multiplexing (FDM). This technique uses various frequencies to combine streams of data, for sending them on a communication medium, as a single signal.

Example − A traditional television transmitter, which sends a number of channels through a single cable uses FDM.

Wavelength Division Multiplexing

Wavelength Division multiplexing (WDM) is an analog technique, in which many data streams of different wavelengths are transmitted in the light spectrum. If the wavelength increases, the frequency of the signal decreases. A prism, which can turn different wavelengths into a single line, can be used at the output of MUX and input of DEMUX.

Example − Optical fiber communications use WDM technique, to merge different wavelengths into a single light for communication.

Digital Multiplexing

The term digital represents the discrete bits of information. Hence, the available data is in the form of frames or packets, which are discrete.

Time Division Multiplexing

In Time Division Multiplexing (TDM), the time frame is divided into slots. This technique is used to transmit a signal over a single communication channel, by allotting one slot for each message.

Time Division Multiplexing (TDM) can be classified into Synchronous TDM and Asynchronous TDM.

Synchronous TDM

In Synchronous TDM, the input is connected to a frame. If there are ‘n’ number of connections, then the frame is divided into ‘n’ time slots. One slot is allocated for each input line.

In this technique, the sampling rate is common for all signals and hence the same clock input is given. The MUX allocates the same slot to each device at all times.

Asynchronous TDM

In Asynchronous TDM, the sampling rate is different for each of the signals and a common clock is not required. If the allotted device for a time slot transmits nothing and sits idle, then that slot can be allotted to another device, unlike synchronous

This type of TDM is used in Asynchronous transfer mode networks.

De-Multiplexer

De-multiplexers are used to connect a single source to multiple destinations. This process is the reverse process of multiplexing. As mentioned previously, it is used mostly at the receivers. DEMUX has many applications. It is used in receivers in the communication systems. It is used in arithmetic and logical unit in computers to supply power and to pass on communication, etc.

De-multiplexers are used as serial to parallel converters. The serial data is given as input to DEMUX at regular interval and a counter is attached to it to control the output of the de-multiplexer.

Both the multiplexers and de-multiplexers play an important role in communication systems, both at the transmitter and the receiver sections.

In any communication system, during the transmission of the signal or while receiving the signal, some unwanted signal gets introduced into the communication, making it unpleasant for the receiver, and questioning the quality of the communication. Such a disturbance is called as Noise.

What is Noise?

Noise is an unwanted signal, which interferes with the original message signal and corrupts the parameters of the message signal. This alteration in the communication process, leads to the message getting altered. It most likely enters at the channel or the receiver.

The noise signal can be understood by taking a look at the following figure.

Hence, it is understood that the noise is some signal which has no pattern and no constant frequency or amplitude. It is quite random and unpredictable. Measures are usually taken to reduce it, though it can’t be completely eliminated.

Most common examples of noise are −

• Hiss sound in radio receivers

• Buzz sound amidst of telephone conversations

• Flicker in television receivers, etc

Types of Noise

The classification of noise is done depending on the type of the source, the effect it shows or the relation it has with the receiver, etc.

There are two main ways in which noise is produced. One is through some external source while the other is created by an internal source, within the receiver section.

External Source

This noise is produced by the external sources, which may occur in the medium or channel of communication usually. This noise cannot be completely eliminated. The best way is to avoid the noise from affecting the signal.

Examples

Most common examples of this type of noise are

• Atmospheric noise (due to irregularities in the atmosphere).

• Extra-terrestrial noise, such as solar noise and cosmic noise.

• Industrial noise.

Internal Source

This noise is produced by the receiver components while functioning. The components in the circuits, due to continuous functioning, may produce few types of noise. This noise is quantifiable. A proper receiver design may lower the effect of this internal noise.

Examples

Most common examples of this type of noise are

• Thermal agitation noise (Johnson noise or Electrical noise)

• Shot noise (due to the random movement of electrons and holes)

• Transit-time noise (during transition)

• Miscellaneous noise is another type of noise which includes flicker, resistance effect and mixer generated noise, etc.

Effects of Noise

Noise is an inconvenient feature, which affects the system performance. Following are the effects of noise.

Noise limits the operating range of the systems

Noise indirectly places a limit on the weakest signal that can be amplified by an amplifier. The oscillator in the mixer circuit may limit its frequency because of noise. A system’s operation depends on the operation of its circuits. Noise limits the smallest signal that a receiver is capable of processing.

Noise affects the sensitivity of receivers

Sensitivity is the minimum amount of input signal necessary to obtain the specified quality output. Noise affects the sensitivity of a receiver system, which eventually affects the output.

In this chapter, let us calculate Signal to Noise Ratios and Figure of Merits of various modulated waves, which are demodulated at the receiver.

Signal to Noise Ratio

Signal-to-Noise Ratio (SNR) is the ratio of the signal power to noise power. The higher the value of SNR, the greater will be the quality of the received output.

Signal-to-Noise Ratio at different points can be calculated using the following formulas.

Input SNR = $\left ( SNR \right )_I= \frac{Average \:\: power \:\:of \:\:modulating \:\:signal}{Average\:\: power \:\:of \:\:noise \:\:at \:\:input}$

Output SNR = $\left ( SNR \right )_O= \frac{Average \:\: power \:\:of \:\:demodulated \:\:signal}{Average\:\: power \:\:of \:\:noise \:\:at \:\:output}$

Channel SNR = $\left ( SNR \right )_C= \frac{Average \:\: power \:\:of \:\:modulated \:\:signal}{Average\:\: power \:\:of \:\:noise \:\:in \:\:message \:\:bandwidth}$

Figure of Merit

The ratio of output SNR and input SNR can be termed as Figure of Merit. It is denoted by F. It describes the performance of a device.

$$F=\frac {\left ( SNR \right )_O}{\left ( SNR \right )_I}$$

Figure of merit of a receiver is

$$F=\frac {\left ( SNR \right )_O}{\left ( SNR \right )_C}$$

It is so because for a receiver, the channel is the input.

SNR Calculations in AM System

Consider the following receiver model of AM system to analyze noise.

We know that the Amplitude Modulated (AM) wave is

$$s\left ( t \right )=A_c\left [ 1+k_am\left ( t \right ) \right ] \cos\left ( 2 \pi f_ct \right )$$

$$\Rightarrow s\left ( t \right )=A_c \cos \left ( 2 \pi f_ct \right )+A_ck_am\left ( t \right ) \cos\left ( 2 \pi f_ct \right )$$

Average power of AM wave is

$$P_s=\left ( \frac{A_c}{\sqrt{2}} \right )^2+\left ( \frac{A_ck_am\left ( t \right )}{\sqrt{2}} \right )^2=\frac{{A_{c}}^{2}}{2}+\frac{{A_{c}}^{2}{k_{a}}^{2}P}{2}$$

$$\Rightarrow P_s=\frac{{A_{c}}^{2}\left ( 1+{k_{a}}^{2}P \right )}{2}$$

Average power of noise in the message bandwidth is

$$P_{nc}=WN_0$$

Substitute, these values in channel SNR formula

$$\left ( SNR \right )_{C,AM}=\frac{Average \:\: Power \:\: of \:\: AM \:\: Wave}{Average \:\: Power \:\: of \:\: noise \:\: in \:\: message \:\: bandwidth}$$

$$\Rightarrow \left ( SNR \right )_{C,AM}=\frac{{A_{c}}^{2}\left ( 1+ {k_{a}}^{2}\right )P}{2WN_0}$$

Where,

• P is the power of the message signal=$\frac{{A_{m}}^{2}}{2}$

• W is the message bandwidth

Assume the band pass noise is mixed with AM wave in the channel as shown in the above figure. This combination is applied at the input of AM demodulator. Hence, the input of AM demodulator is.

$$v\left ( t \right )=s\left ( t \right )+n\left ( t \right )$$

$\Rightarrow v\left ( t \right )=A_c\left [ 1+k_am\left ( t \right ) \right ] \cos\left ( 2 \pi f_ct \right )+$

$\left [ n_1\left ( t \right ) \cos\left ( 2 \pi f_ct \right ) - n_Q\left ( t \right ) \sin \left ( 2 \pi f_ct \right )\right ]$

$\Rightarrow v\left ( t \right )=\left [ A_c+A_ck_am\left ( t \right )+n_1\left ( t \right ) \right ] \cos\left ( 2 \pi f_ct \right )-n_Q\left ( t \right ) \sin\left ( 2 \pi f_ct \right )$

Where $n_I \left ( t \right )$ and $n_Q \left ( t \right )$ are in phase and quadrature phase components of noise.

The output of AM demodulator is nothing but the envelope of the above signal.

$$d\left ( t \right )=\sqrt{\left [ A_c+A_cK_am\left ( t \right )+n_I\left ( t \right ) \right ]^2+\left ( n_Q\left ( t \right ) \right )^2}$$

$$\Rightarrow d\left ( t \right )\approx A_c+A_ck_am\left ( t \right )+n_1\left ( t \right )$$

Average power of the demodulated signal is

$$P_m=\left ( \frac{A_ck_am\left ( t \right )}{\sqrt{2}} \right )^2=\frac{{A_{c}}^{2}{k_{a}}^{2}P}{2}$$

Average power of noise at the output is

$$P_no=WN_0$$

Substitute, these values in output SNR formula.

$$\left ( SNR \right )_{O,AM}= \frac {Average \:\: Power \:\: of \:\: demodulated \:\: signal }{Average \:\: Power \:\: of \:\: noise \:\: at \:\: Output}$$

$$\Rightarrow \left ( SNR \right )_{O,AM}=\frac{{A_{c}}^{2}{k_{a}}^{2}P}{2WN_0}$$

Substitute, the values in Figure of merit of AM receiver formula.

$$F=\frac{\left ( SNR \right )_{O,AM}}{\left ( SNR \right )_{C,AM}}$$

$$\Rightarrow F=\left ( \frac{{A_{c}^{2}}{k_{a}^{2}}P}{2WN_0} \right )/\left ( \frac{{A_{c}}^{2}\left ( 1+ {k_{a}}^{2}\right )P}{2WN_0} \right )$$

$$\Rightarrow F=\frac{{K_{a}}^{2}P}{1+{K_{a}}^{2}P}$$

Therefore, the Figure of merit of AM receiver is less than one.

SNR Calculations in DSBSC System

Consider the following receiver model of DSBSC system to analyze noise.

We know that the DSBSC modulated wave is

$$s\left ( t \right )=A_cm\left ( t \right ) \cos\left ( 2 \pi f_ct \right )$$

Average power of DSBSC modulated wave is

$$P_s=\left ( \frac{A_cm\left ( t \right )}{\sqrt{2}} \right )^2=\frac{{A_{c}}^{2}P}{2}$$

Average power of noise in the message bandwidth is

$$P_{nc}=WN_0$$

Substitute, these values in channel SNR formula.

$$\left ( SNR \right )_{C,DSBSC}=\frac{Average \:\: Power \:\: of \:\: DSBSC \:\: modulated \:\: wave}{Average \:\: Power \:\: of \:\: noise \:\: in \:\: message \:\: bandwidth}$$

$$\Rightarrow \left ( SNR \right )_{C,DSBSC}=\frac{{A_{c}}^{2}P}{2WN_0}$$

Assume the band pass noise is mixed with DSBSC modulated wave in the channel as shown in the above figure. This combination is applied as one of the input to the product modulator. Hence, the input of this product modulator is

$$v_1\left ( t \right )=s\left ( t \right )+n\left ( t \right )$$

$$\Rightarrow v_1\left ( t \right )=A_cm\left ( t \right ) \cos \left ( 2 \pi f_ct \right )+\left [ n_I\left ( t \right ) \cos\left ( 2 \pi f_ct \right ) - n_Q\left ( t \right ) \sin \left ( 2 \pi f_ct \right )\right ]$$

$$\Rightarrow v_1\left ( t \right )=\left [ A_cm \left ( t \right ) +n_I\left ( t \right ) \right ] \cos\left ( 2 \pi f_ct \right )-n_Q\left ( t \right ) \sin\left ( 2 \pi f_ct \right )$$

Local oscillator generates the carrier signal $c\left ( t \right )= \cos\left ( 2 \pi f_ct \right )$. This signal is applied as another input to the product modulator. Therefore, the product modulator produces an output, which is the product of $v_1\left ( t \right )$ and $c\left ( t \right )$.

$$v_2\left ( t \right )= v_1\left ( t \right )c\left ( t \right )$$

Substitute, $v_1\left ( t \right )$ and $c\left ( t \right )$ values in the above equation.

$$\Rightarrow v_2\left ( t \right )=\left ( \left [ A_cm\left ( t \right ) + n_I\left ( t \right )\right ] \cos\left ( 2 \pi f_ct \right )- n_Q\left ( t \right ) \sin\left ( 2 \pi f_ct \right ) \right ) \cos\left ( 2 \pi f_ct \right )$$

$$\Rightarrow v_2\left ( t \right )=\left [ A_c m\left ( t \right )+n_I\left ( t \right ) \right ] \cos^2\left ( 2 \pi f_ct \right )-n_Q\left ( t \right ) \sin\left ( 2 \pi f_ct \right ) \cos\left ( 2 \pi f_ct \right )$$

$$\Rightarrow v_2\left ( t \right )=\left [ A_c m\left ( t \right )+n_I\left ( t \right ) \right ] \left ( \frac{1+ \cos\left ( 4 \pi f_ct \right )}{2} \right ) -n_Q\left ( t \right )\frac{ \sin\left ( 4 \pi f_ct \right )}{2}$$

When the above signal is applied as an input to low pass filter, we will get the output of low pass filter as

$$d\left ( t \right )=\frac{\left [ A_c m\left ( t \right )+n_I\left ( t \right ) \right ]}{2}$$

Average power of the demodulated signal is

$$P_m=\left ( \frac{A_cm\left ( t \right )}{2\sqrt{2}} \right )^2=\frac{{A_{c}}^{2}P}{8}$$

Average power of noise at the output is

$$P_{no}=\frac{WN_0}{4}$$

Substitute, these values in output SNR formula.

$$\left ( SNR \right )_{O,DSBSC}= \frac {Average \:\: Power \:\: of \:\: demodulated \:\: signal }{Average \:\: Power \:\: of \:\: noise \:\: at \:\: Output}$$

$$\Rightarrow \left ( SNR \right )_{O,DSBSC}=\left ( \frac{{A_{c}}^{2}P}{8} \right )/ \left ( \frac{WN_0}{4} \right )=\frac{{A_{c}}^{2}P}{2WN_0}$$

Substitute, the values in Figure of merit of DSBSC receiver formula.

$$F=\frac{\left ( SNR \right )_{O,DSBSC}}{\left ( SNR \right )_{C,DSBSC}}$$

$$\Rightarrow F= \left ( \frac{{A_{c}}^{2}P}{2WN_0} \right )/ \left ( \frac{{A_{c}}^{2}P}{2WN_0} \right )$$

$$\Rightarrow F= 1$$

Therefore, the Figure of merit of DSBSC receiver is 1.

SNR Calculations in SSBSC System

Consider the following receiver model of SSBSC system to analyze noise.

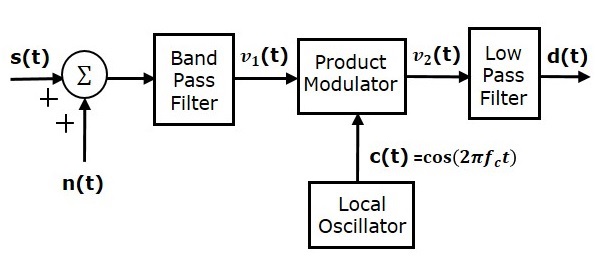
We know that the SSBSC modulated wave having lower sideband is

$$s\left ( t \right )=\frac{A_mA_c}{2} \cos \left [ 2 \pi\left ( f_c-f_m \right )t \right ]$$

Average power of SSBSC modulated wave is

$$P_s=\left ( \frac{A_mA_c}{2\sqrt{2}} \right )^2=\frac{{A_{m}}^{2}{A_{c}}^{2}}{8}$$

Average power of noise in the message bandwidth is

$$P_{nc}=WN_0$$

Substitute, these values in channel SNR formula.

$$\left ( SNR \right )_{C,SSBSC}= \frac {Average \:\: Power \:\: of \:\: SSBSC \:\: modulated \:\: wave}{Average \:\: Power \:\: of \:\: noise \:\: in\:\: message \:\: bandwidth}$$

$$\Rightarrow \left ( SNR \right )_{C,SSBSC}=\frac{{A_{m}}^{2}{A_{c}}^{2}}{8WN_0}$$

Assume the band pass noise is mixed with SSBSC modulated wave in the channel as shown in the above figure. This combination is applied as one of the input to the product modulator. Hence, the input of this product modulator is

$$v_1\left ( t \right )=s\left ( t \right )+n\left ( t \right )$$

$$v_1\left ( t \right )=\frac{A_mA_c}{2} \cos\left [ 2 \pi \left ( f_c-f_m \right )t \right ] + n_I\left ( t \right ) \cos\left ( 2 \pi f_ct \right )-n_Q\left ( t \right ) \sin \left ( 2 \pi f_ct \right )$$

The local oscillator generates the carrier signal $c\left ( t \right )= \cos \left ( 2 \pi f_ct \right ) $. This signal is applied as another input to the product modulator. Therefore, the product modulator produces an output, which is the product of $v_1\left ( t \right )$ and $c\left ( t \right )$.

$$v_2\left ( t \right )=v_1\left ( t \right )c \left ( t \right )$$

Substitute, $v_1\left ( t \right )$ and $ c\left ( t \right )$ values in the above equation.

$\Rightarrow v_2(t)= (\frac{A_mA_c}{2} \cos[ 2 \pi ( f_c-f_m )t ] + n_I ( t ) \cos ( 2 \pi f_ct )-$

$n_Q( t ) \sin ( 2 \pi f_ct ) )\cos ( 2 \pi f_ct )$

$\Rightarrow v_2\left ( t \right )=\frac{A_mA_c}{2} \cos\left [ 2 \pi \left ( f_c-f_m \right )t \right ] \cos\left ( 2 \pi f_ct \right )+$

$n_I\left ( t \right ) \cos^2\left ( 2 \pi f_ct \right )-n_Q\left ( t \right ) \sin\left ( 2 \pi f_ct \right ) \cos\left ( 2 \pi f_ct \right )$

$\Rightarrow v_2\left ( t \right )=\frac{A_mA_c}{4} \left \{ \cos\left [ 2 \pi\left ( 2f_c-f_m \right )t \right ] + \cos \left ( 2 \pi f_mt \right )\right \}+$

$n_I\left ( t \right )\left ( \frac{1+ \cos\left ( 4 \pi f_ct \right )}{2} \right )- n_Q\left ( t \right )\frac{\sin \left ( 4 \pi f_ct \right )}{2}$

When the above signal is applied as an input to low pass filter, we will get the output of low pass filter as

$$d\left ( t \right )=\frac{A_mA_c}{2} \cos\left ( 2 \pi f_mt \right )+\frac{n_I\left ( t \right )}{2}$$

Average power of the demodulated signal is

$$P_m=\left ( \frac{A_mA_c}{4\sqrt{2}} \right )^2=\frac{{A_{m}}^{2}{A_{c}}^{2}}{32}$$

Average power of noise at the output is

$$P_{no}=\frac{WN_0}{4}$$

Substitute, these values in output SNR formula

$$\left ( SNR \right )_{O,SSBSC}= \frac {Average \:\: Power \:\: of \:\: demodulated \:\: signal}{Average \:\: Power \:\: of \:\: noise \:\: at \:\: output}$$

$$\Rightarrow \left ( SNR \right )_{O,SSBSC}= \left ( \frac{{A_{m}}^{2}{A_{c}}^{2}}{32} \right )/\left ( \frac{WN_0}{4} \right )=\frac{{A_{m}}^{2}{A_{c}}^{2}}{8WN_0}$$

Substitute, the values in Figure of merit of SSBSC receiver formula

$$F=\frac{\left ( SNR \right )_{O,SSBSC}}{\left ( SNR \right )_{C,SSBSC}}$$

$$F=\left ( \frac{{A_{m}}^{2}{A_{c}}^{2}}{8WN_0} \right )/\left ( \frac{{A_{m}}^{2}{A_{c}}^{2}}{8WN_0} \right )$$

$$F=1$$

Therefore, the Figure of merit of SSBSC receiver is 1.

The antenna present at the end of transmitter section, transmits the modulated wave. In this chapter, let us discuss about AM and FM transmitters.

AM Transmitter

AM transmitter takes the audio signal as an input and delivers amplitude modulated wave to the antenna as an output to be transmitted. The block diagram of AM transmitter is shown in the following figure.

The working of AM transmitter can be explained as follows.

• The audio signal from the output of the microphone is sent to the pre-amplifier, which boosts the level of the modulating signal.

• The RF oscillator generates the carrier signal.

• Both the modulating and the carrier signal is sent to AM modulator.

• Power amplifier is used to increase the power levels of AM wave. This wave is finally passed to the antenna to be transmitted.

FM Transmitter

FM transmitter is the whole unit, which takes the audio signal as an input and delivers FM wave to the antenna as an output to be transmitted. The block diagram of FM transmitter is shown in the following figure.

The working of FM transmitter can be explained as follows.

• The audio signal from the output of the microphone is sent to the pre-amplifier, which boosts the level of the modulating signal.

• This signal is then passed to high pass filter, which acts as a pre-emphasis network to filter out the noise and improve the signal to noise ratio.

• This signal is further passed to the FM modulator circuit.

• The oscillator circuit generates a high frequency carrier, which is sent to the modulator along with the modulating signal.

• Several stages of frequency multiplier are used to increase the operating frequency. Even then, the power of the signal is not enough to transmit. Hence, a RF power amplifier is used at the end to increase the power of the modulated signal. This FM modulated output is finally passed to the antenna to be transmitted.

The antenna present at the beginning of the receiver section, receives the modulated wave. First let us discuss the requirements of a receiver.

Requirements of a Receiver

AM receiver receives AM wave and demodulates it by using the envelope detector. Similarly, FM receiver receives FM wave and demodulates it by using the Frequency Discrimination method. Following are the requirements of both AM and FM receiver.

• It should be cost-effective.

• It should receive the corresponding modulated waves.

• The receiver should be able to tune and amplify the desired station.

• It should have an ability to reject the unwanted stations.

• Demodulation has to be done to all the station signals, irrespective of the carrier signal frequency.

For these requirements to be fulfilled, the tuner circuit and the mixer circuit should be very effective. The procedure of RF mixing is an interesting phenomenon.

RF Mixing

The RF mixing unit develops an Intermediate Frequency (IF) to which any received signal is converted, so as to process the signal effectively.

RF Mixer is an important stage in the receiver. Two signals of different frequencies are taken where one signal level affects the level of the other signal, to produce the resultant mixed output. The input signals and the resultant mixer output is illustrated in the following figures.

Let the first and second signal frequencies be $f_1$ and $f_2$. If these two signals are applied as inputs of RF mixer, then it produces an output signal, having frequencies of $f_1+f_2$ and $f_1-f_2$.

If this is observed in the frequency domain, the pattern looks like the following figure.

In this case, $f_1$ is greater than $f_2$. So, the resultant output has frequencies $f_1+f_2$ and $f_1-f_2$. Similarly, if $f_2$ is greater than $f_1$, then the resultant output will have the frequencies $f_1+f_2$ and $f_1-f_2$.

AM Receiver

The AM super heterodyne receiver takes the amplitude modulated wave as an input and produces the original audio signal as an output. Selectivity is the ability of selecting a particular signal, while rejecting the others. Sensitivity is the capacity of detecting RF signal and demodulating it, while at the lowest power level.

Radio amateurs are the initial radio receivers. However, they have drawbacks such as poor sensitivity and selectivity. To overcome these drawbacks, super heterodyne receiver was invented. The block diagram of AM receiver is shown in the following figure.

RF Tuner Section

The amplitude modulated wave received by the antenna is first passed to the tuner circuit through a transformer. The tuner circuit is nothing but a LC circuit, which is also called as resonant or tank circuit. It selects the frequency, desired by the AM receiver. It also tunes the local oscillator and the RF filter at the same time.

RF Mixer

The signal from the tuner output is sent to the RF-IF converter, which acts as a mixer. It has a local oscillator, which produces a constant frequency. The mixing process is done here, having the received signal as one input and the local oscillator frequency as the other input. The resultant output is a mixture of two frequencies $\left [ \left ( f_1+f_2 \right ) , \left ( f_1-f_2 \right )\right ]$ produced by the mixer, which is called as the Intermediate Frequency (IF).

The production of IF helps in the demodulation of any station signal having any carrier frequency. Hence, all signals are translated to a fixed carrier frequency for adequate selectivity.

IF Filter

Intermediate frequency filter is a band pass filter, which passes the desired frequency. It eliminates all other unwanted frequency components present in it. This is the advantage of IF filter, which allows only IF frequency.

AM Demodulator

The received AM wave is now demodulated using AM demodulator. This demodulator uses the envelope detection process to receive the modulating signal.

Audio Amplifier

This is the power amplifier stage, which is used to amplify the detected audio signal. The processed signal is strengthened to be effective. This signal is passed on to the loudspeaker to get the original sound signal.

FM Receiver

The block diagram of FM receiver is shown in the following figure.

This block diagram of FM receiver is similar to the block diagram of AM receiver. The two blocks Amplitude limiter and De-emphasis network are included before and after FM demodulator. The operation of the remaining blocks is the same as that of AM receiver.

We know that in FM modulation, the amplitude of FM wave remains constant. However, if some noise is added with FM wave in the channel, due to that the amplitude of FM wave may vary. Thus, with the help of amplitude limiter we can maintain the amplitude of FM wave as constant by removing the unwanted peaks of the noise signal.

In FM transmitter, we have seen the pre-emphasis network (High pass filter), which is present before FM modulator. This is used to improve the SNR of high frequency audio signal. The reverse process of pre-emphasis is known as de-emphasis. Thus, in this FM receiver, the de-emphasis network (Low pass filter) is included after FM demodulator. This signal is passed to the audio amplifier to increase the power level. Finally, we get the original sound signal from the loudspeaker.

So far, we have discussed about continuous-wave modulation. We will discuss about pulse modulation in the next chapter. These pulse modulation techniques deal with discrete signals. So, now let us see how to convert a continuous time signal into a discrete one.

The process of converting continuous time signals into equivalent discrete time signals, can be termed as Sampling. A certain instant of data is continually sampled in the sampling process.

The following figure shows a continuous-time signal x(t) and the corresponding sampled signal x_s(t). When x(t) is multiplied by a periodic impulse train, the sampled signal x_s(t) is obtained.

A sampling signal is a periodic train of pulses, having unit amplitude, sampled at equal intervals of time $T_s$, which is called as sampling time. This data is transmitted at the time instants $T_s$ and the carrier signal is transmitted at the remaining time.

Sampling Rate

To discretize the signals, the gap between the samples should be fixed. That gap can be termed as the sampling period $T_s$. Reciprocal of the sampling period is known as sampling frequency or sampling rate $f_s$.

Mathematically, we can write it as

$$f_s= \frac{1}{T_s}$$

Where,

$f_s$ is the sampling frequency or the sampling rate

$T_s$ is the sampling period

Sampling Theorem

The sampling rate should be such that the data in the message signal should neither be lost nor it should get over-lapped. The sampling theorem states that, “a signal can be exactly reproduced if it is sampled at the rate $f_s$, which is greater than or equal to twice the maximum frequency of the given signal W.”

Mathematically, we can write it as

$$f_s\geq 2W$$

Where,

• $f_s$ is the sampling rate

• $W$ is the highest frequency of the given signal

If the sampling rate is equal to twice the maximum frequency of the given signal W, then it is called as Nyquist rate.

The sampling theorem, which is also called as Nyquist theorem, delivers the theory of sufficient sample rate in terms of bandwidth for the class of functions that are bandlimited.

For continuous-time signal x(t), which is band-limited in the frequency domain is represented as shown in the following figure.

If the signal is sampled above Nyquist rate, then the original signal can be recovered. The following figure explains a signal, if sampled at a higher rate than 2w in the frequency domain.

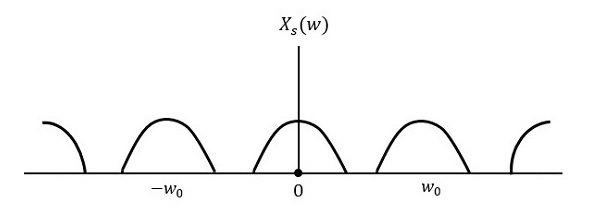
If the same signal is sampled at a rate less than 2w, then the sampled signal would look like the following figure.

We can observe from the above pattern that there is over-lapping of information, which leads to mixing up and loss of information. This unwanted phenomenon of over-lapping is called as Aliasing.

Aliasing can be referred to as “the phenomenon of a high-frequency component in the spectrum of a signal, taking on the identity of a low-frequency component in the spectrum of its sampled version.”

Hence, the sampling rate of the signal is chosen to be as Nyquist rate. If the sampling rate is equal to twice the highest frequency of the given signal W, then the sampled signal would look like the following figure.

In this case, the signal can be recovered without any loss. Hence, this is a good sampling rate.

After continuous wave modulation, the next division is Pulse modulation. In this chapter, let us discuss the following analog pulse modulation techniques.

• Pulse Amplitude Modulation
• Pulse Width Modulation
• Pulse Position Modulation

Pulse Amplitude Modulation

In Pulse Amplitude Modulation (PAM) technique, the amplitude of the pulse carrier varies, which is proportional to the instantaneous amplitude of the message signal.

The pulse amplitude modulated signal will follow the amplitude of the original signal, as the signal traces out the path of the whole wave. In natural PAM, a signal sampled at Nyquist rate can be reconstructed, by passing it through an efficient Low Pass Filter (LPF) with exact cutoff frequency.

The following figures explain the Pulse Amplitude Modulation.

Though the PAM signal is passed through a LPF, it cannot recover the signal without distortion. Hence, to avoid this noise, use flat-top sampling. The flat-top PAM signal is shown in the following figure.

Flat-top sampling is the process in which, the sampled signal can be represented in pulses for which the amplitude of the signal cannot be changed with respect to the analog signal, to be sampled. The tops of amplitude remain flat. This process simplifies the circuit design.

Pulse Width Modulation

In Pulse Width Modulation (PWM) or Pulse Duration Modulation (PDM) or Pulse Time Modulation (PTM) technique, the width or the duration or the time of the pulse carrier varies, which is proportional to the instantaneous amplitude of the message signal.

The width of the pulse varies in this method, but the amplitude of the signal remains constant. Amplitude limiters are used to make the amplitude of the signal constant. These circuits clip off the amplitude to a desired level, and hence the noise is limited.

The following figure explains the types of Pulse Width Modulations.

There are three types of PWM.

• The leading edge of the pulse being constant, the trailing edge varies according to the message signal. The waveform for this type of PWM is denoted as (a) in the above figure.

• The trailing edge of the pulse being constant, the leading edge varies according to the message signal. The waveform for this type of PWM is denoted as (b) in the above figure.

• The center of the pulse being constant, the leading edge and the trailing edge varies according to the message signal. The waveform for this type of PWM is denoted as (c) shown in the above figure.

Pulse Position Modulation

Pulse Position Modulation (PPM) is an analog modulation scheme in which, the amplitude and the width of the pulses are kept constant, while the position of each pulse, with reference to the position of a reference pulse varies according to the instantaneous sampled value of the message signal.

The transmitter has to send synchronizing pulses (or simply sync pulses) to keep the transmitter and the receiver in sync. These sync pulses help to maintain the position of the pulses. The following figures explain the Pulse Position Modulation.

Pulse position modulation is done in accordance with the pulse width modulated signal. Each trailing edge of the pulse width modulated signal becomes the starting point for pulses in PPM signal. Hence, the position of these pulses is proportional to the width of the PWM pulses.

Advantage

As the amplitude and the width are constant, the power handled is also constant.

Disadvantage

The synchronization between the transmitter and the receiver is a must.

Comparison between PAM, PWM, and PPM

The following table presents the comparison between three modulation techniques.

PAM	PWM	PPM
Amplitude is varied	Width is varied	Position is varied
Bandwidth depends on the width of the pulse	Bandwidth depends on the rise time of the pulse	Bandwidth depends on the rise time of the pulse
Instantaneous transmitter power varies with the amplitude of the pulses	Instantaneous transmitter power varies with the amplitude and the width of the pulses	Instantaneous transmitter power remains constant with the width of the pulses
System complexity is high	System complexity is low	System complexity is low
Noise interference is high	Noise interference is low	Noise interference is low
It is similar to amplitude modulation	It is similar to frequency modulation	It is similar to phase modulation

Transducer is a device, which converts energy from one form to other. In this chapter, let us discuss about the transducers used in communication systems.

Why do We Need Transducers?

In the real world, communication between any two nearby persons takes place with the help of sound waves. But, if the persons are far away, then it is difficult to convey the information without any loss by using sound waves in its physical form.

To overcome this difficulty, we can use modulators in the transmitter section and demodulators in the receiver section. These modulators and demodulators operate with electrical signals. That’s why we require a device, which has to convert the sound waves into electrical signals or vice versa. That device is known as a transducer.

Following is a simple block diagram of a transducer.

This transducer has a single input and a single output. It converts the energy present at the input into its equivalent output having another energy. Basically, a transducer converts the non-electrical form of energy into an electrical form or vice versa.

Types of Transducers

We can classify the transducers into following two types based on the placement (position) of the transducer in communication systems.

• Input Transducer
• Output Transducer

Input Transducers

The transducer present at the input of the communication system is known as an input transducer. Following is the block diagram of an input transducer.

This input transducer converts the non-electrical physical quantity into an electrical signal. The physical quantities such as sound or light can be converted into electrical quantities such as voltage or current by using this transducer. Example: Microphone.

Microphone is used as the input transducer, which is placed between the information source and the transmitter section. The information source produces the information in the form of sound waves. The microphone converts these sound waves into electrical signals with the help of a diaphragm. These electrical signals can be used for further processing.

Output Transducers

The transducer present at the output of communication system is known as output transducer. Following is the block diagram of an output transducer.

This output transducer converts the electrical signal into non-electrical physical quantity. The electrical quantities such as voltage or current can be converted into physical quantities such as sound or light by using this transducer. Example: Loudspeaker.

The loud speaker is used as the output transducer, which is placed between the receiver section and the destination. The demodulator present in the receiver section produces the demodulated output. So, the loud speaker converts the electrical signals (demodulated output) into sound waves. Therefore, the functionality of the loud speaker is just opposite to the functionality of the microphone.

In addition to the above transducers, there is one more transducer which is used in communication systems. This transducer can be placed either at the end of the transmitter section or at the starting of the receiver section. Example: Antenna.

An Antenna is a transducer, which converts electrical signals into electromagnetic waves and vice versa. An Antenna can be used either as a transmitting antenna or as a receiving antenna.

A transmitting antenna converts electrical signals into electromagnetic waves and radiates them. While, a receiving antenna converts electromagnetic waves from the received beam into electrical signals.

In this two-way communication, the same antenna can be used for both transmission and reception.