Komunikasi Analog - Perhitungan SNR

Dalam bab ini, mari kita menghitung Rasio Sinyal terhadap Derau dan Gambar Manfaat dari berbagai gelombang termodulasi, yang didemodulasi di penerima.

Sinyal untuk rasio kebisingan

Signal-to-Noise Ratio (SNR)adalah rasio daya sinyal terhadap daya derau. Semakin tinggi nilai SNR, semakin besar kualitas keluaran yang diterima.

Rasio Signal-to-Noise di berbagai titik dapat dihitung dengan menggunakan rumus berikut.

Input SNR = $ \ kiri (SNR \ kanan) _I = \ frac {Rata-rata \: \: daya \: \: dari \: \: modulasi \: \: sinyal} {Rata-rata \: \: daya \: \: dari \: \: noise \: \: at \: \: input} $

Output SNR = $ \ kiri (SNR \ kanan) _O = \ frac {Rata-rata \: \: power \: \: dari \: \: demodulated \: \: signal} {Average \: \: power \: \: of \: \: noise \: \: at \: \: output} $

Channel SNR = $ \ kiri (SNR \ kanan) _C = \ frac {Rata-rata \: \: power \: \: dari \: \: modulated \: \: signal} {Average \: \: power \: \: of \: \: noise \: \: in \: \: message \: \: bandwidth} $

Sosok Merit

Rasio output SNR dan input SNR dapat disebut sebagai Figure of Merit. Ini dilambangkan denganF. Ini menggambarkan kinerja perangkat.

$$ F = \ frac {\ kiri (SNR \ kanan) _O} {\ kiri (SNR \ kanan) _I} $$

Sosok manfaat penerima adalah

$$ F = \ frac {\ kiri (SNR \ kanan) _O} {\ kiri (SNR \ kanan) _C} $$

Karena bagi penerima, saluran adalah inputnya.

Perhitungan SNR di Sistem AM

Pertimbangkan model penerima sistem AM berikut untuk menganalisis kebisingan.

Kita tahu bahwa gelombang Amplitude Modulated (AM) adalah

$$ s \ kiri (t \ kanan) = A_c \ kiri [1 + k_am \ kiri (t \ kanan) \ kanan] \ cos \ kiri (2 \ pi f_ct \ kanan) $$

$$ \ Panah kanan s \ kiri (t \ kanan) = A_c \ cos \ kiri (2 \ pi f_ct \ kanan) + A_ck_am \ kiri (t \ kanan) \ cos \ kiri (2 \ pi f_ct \ kanan) $$

Kekuatan rata-rata gelombang AM adalah

$$ P_s = \ left (\ frac {A_c} {\ sqrt {2}} \ right) ^ 2 + \ left (\ frac {A_ck_am \ left (t \ right)} {\ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2}} {2} + \ frac {{A_ {c}} ^ {2} {k_ {a}} ^ {2} P} {2} $ $

$$ \ Rightarrow P_s = \ frac {{A_ {c}} ^ {2} \ kiri (1+ {k_ {a}} ^ {2} P \ kanan)} {2} $$

Daya rata-rata noise dalam bandwidth pesan adalah

$$ P_ {nc} = WN_0 $$

Gantikan, nilai-nilai ini dalam channel SNR rumus

$$ \ kiri (SNR \ kanan) _ {C, AM} = \ frac {Rata-rata \: \: Daya \: \: dari \: \: AM \: \: Gelombang} {Rata-rata \: \: Daya \: \: dari \: \: noise \: \: in \: \: message \: \: bandwidth} $$

$$ \ Rightarrow \ left (SNR \ right) _ {C, AM} = \ frac {{A_ {c}} ^ {2} \ left (1+ {k_ {a}} ^ {2} \ kanan) P } {2WN_0} $$

Dimana,

P adalah kekuatan sinyal pesan = $ \ frac {{A_ {m}} ^ {2}} {2} $
W adalah bandwidth pesan

Diasumsikan band pass noise bercampur dengan gelombang AM di channel seperti yang ditunjukkan pada gambar di atas. Kombinasi ini diterapkan pada input demodulator AM. Oleh karena itu, input dari demodulator AM adalah.

$$ v \ kiri (t \ kanan) = s \ kiri (t \ kanan) + n \ kiri (t \ kanan) $$

$ \ Rightarrow v \ left (t \ right) = A_c \ kiri [1 + k_am \ kiri (t \ kanan) \ kanan] \ cos \ kiri (2 \ pi f_ct \ kanan) + $

$ \ kiri [n_1 \ kiri (t \ kanan) \ cos \ kiri (2 \ pi f_ct \ kanan) - n_Q \ kiri (t \ kanan) \ sin \ kiri (2 \ pi f_ct \ kanan) \ kanan] $

$ \ Rightarrow v \ left (t \ right) = \ kiri [A_c + A_ck_am \ kiri (t \ kanan) + n_1 \ kiri (t \ kanan) \ kanan] \ cos \ kiri (2 \ pi f_ct \ kanan) - n_Q \ kiri (t \ kanan) \ sin \ kiri (2 \ pi f_ct \ kanan) $

Dimana $ n_I \ left (t \ right) $ dan $ n_Q \ left (t \ right) $ berada dalam komponen fase fase dan fase kuadratur dari kebisingan.

Output dari demodulator AM tidak lain adalah selubung sinyal di atas.

$$ d \ kiri (t \ kanan) = \ sqrt {\ kiri [A_c + A_cK_am \ kiri (t \ kanan) + n_I \ kiri (t \ kanan) \ kanan] ^ 2 + \ kiri (n_Q \ kiri (t \ kanan) \ kanan) ^ 2} $$

$$ \ Panah kanan d \ kiri (t \ kanan) \ sekitar A_c + A_ck_am \ kiri (t \ kanan) + n_1 \ kiri (t \ kanan) $$

Kekuatan rata-rata dari sinyal yang didemodulasi adalah

$$ P_m = \ kiri (\ frac {A_ck_am \ left (t \ right)} {\ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2} {k_ {a} } ^ {2} P} {2} $$

Daya kebisingan rata-rata pada output adalah

$$ P_no = WN_0 $$

Gantikan, nilai-nilai ini dalam output SNR rumus.

$$ \ left (SNR \ right) _ {O, AM} = \ frac {Average \: \: Power \: \: of \: \: demodulated \: \: signal} {Average \: \: Power \: \: dari \: \: noise \: \: at \: \: Output} $$

$$ \ Rightarrow \ left (SNR \ right) _ {O, AM} = \ frac {{A_ {c}} ^ {2} {k_ {a}} ^ {2} P} {2WN_0} $$

Gantikan, nilai dalam Figure of merit rumus penerima AM.

$$ F = \ frac {\ kiri (SNR \ kanan) _ {O, AM}} {\ kiri (SNR \ kanan) _ {C, AM}} $$

$$ \ Rightarrow F = \ kiri (\ frac {{A_ {c} ^ {2}} {k_ {a} ^ {2}} P} {2WN_0} \ kanan) / \ kiri (\ frac {{A_ { c}} ^ {2} \ kiri (1+ {k_ {a}} ^ {2} \ kanan) P} {2WN_0} \ kanan) $$

$$ \ Rightarrow F = \ frac {{K_ {a}} ^ {2} P} {1+ {K_ {a}} ^ {2} P} $$

Oleh karena itu, gambaran manfaat penerima AM kurang dari satu.

Perhitungan SNR dalam Sistem DSBSC

Pertimbangkan model penerima sistem DSBSC berikut untuk menganalisis kebisingan.

Kita tahu bahwa gelombang termodulasi DSBSC adalah

$$ s \ kiri (t \ kanan) = A_cm \ kiri (t \ kanan) \ cos \ kiri (2 \ pi f_ct \ kanan) $$

Daya rata-rata gelombang termodulasi DSBSC adalah

$$ P_s = \ left (\ frac {A_cm \ left (t \ right)} {\ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2} P} {2} $$

Daya rata-rata noise dalam bandwidth pesan adalah

$$ P_ {nc} = WN_0 $$

Gantikan, nilai-nilai ini dalam channel SNR rumus.

$$ \ left (SNR \ right) _ {C, DSBSC} = \ frac {Average \: \: Power \: \: of \: \: DSBSC \: \: modulated \: \: wave} {Rata-rata \: \: Power \: \: of \: \: noise \: \: in \: \: message \: \: bandwidth} $$

$$ \ Rightarrow \ left (SNR \ right) _ {C, DSBSC} = \ frac {{A_ {c}} ^ {2} P} {2WN_0} $$

Asumsikan kebisingan band pass dicampur dengan gelombang termodulasi DSBSC di saluran seperti yang ditunjukkan pada gambar di atas. Kombinasi ini diterapkan sebagai salah satu masukan ke modulator produk. Oleh karena itu, input dari modulator produk ini adalah

$$ v_1 \ kiri (t \ kanan) = s \ kiri (t \ kanan) + n \ kiri (t \ kanan) $$

$$ \ Rightarrow v_1 \ left (t \ right) = A_cm \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) + \ kiri [n_I \ kiri (t \ kanan) \ cos \ kiri ( 2 \ pi f_ct \ kanan) - n_Q \ kiri (t \ kanan) \ sin \ kiri (2 \ pi f_ct \ kanan) \ kanan] $$

$$ \ Rightarrow v_1 \ left (t \ right) = \ kiri [A_cm \ kiri (t \ kanan) + n_I \ kiri (t \ kanan) \ kanan] \ cos \ kiri (2 \ pi f_ct \ kanan) -n_Q \ kiri (t \ kanan) \ sin \ kiri (2 \ pi f_ct \ kanan) $$

Osilator lokal menghasilkan sinyal pembawa $ c \ left (t \ right) = \ cos \ left (2 \ pi f_ct \ right) $. Sinyal ini diterapkan sebagai masukan lain ke modulator produk. Oleh karena itu, modulator produk menghasilkan keluaran, yang merupakan produk dari $ v_1 \ left (t \ right) $ dan $ c \ left (t \ right) $.

$$ v_2 \ kiri (t \ kanan) = v_1 \ kiri (t \ kanan) c \ kiri (t \ kanan) $$

Gantikan, nilai $ v_1 \ left (t \ right) $ dan $ c \ left (t \ right) $ dalam persamaan di atas.

$$ \ Rightarrow v_2 \ left (t \ right) = \ kiri (\ kiri [A_cm \ kiri (t \ kanan) + n_I \ kiri (t \ kanan) \ kanan] \ cos \ kiri (2 \ pi f_ct \ kanan ) - n_Q \ kiri (t \ kanan) \ sin \ kiri (2 \ pi f_ct \ kanan) \ kanan) \ cos \ kiri (2 \ pi f_ct \ kanan) $$

$$ \ Rightarrow v_2 \ left (t \ right) = \ left [A_c m \ left (t \ kanan) + n_I \ kiri (t \ kanan) \ kanan] \ cos ^ 2 \ kiri (2 \ pi f_ct \ kanan ) -n_Q \ kiri (t \ kanan) \ sin \ kiri (2 \ pi f_ct \ kanan) \ cos \ kiri (2 \ pi f_ct \ kanan) $$

$$ \ Rightarrow v_2 \ left (t \ right) = \ kiri [A_c m \ kiri (t \ kanan) + n_I \ kiri (t \ kanan) \ kanan] \ kiri (\ frac {1+ \ cos \ kiri ( 4 \ pi f_ct \ right)} {2} \ right) -n_Q \ left (t \ right) \ frac {\ sin \ left (4 \ pi f_ct \ right)} {2} $$

Ketika sinyal di atas diaplikasikan sebagai input ke filter low pass, kita akan mendapatkan output dari filter low pass sebagai

$$ d \ kiri (t \ kanan) = \ frac {\ kiri [A_c m \ kiri (t \ kanan) + n_I \ kiri (t \ kanan) \ kanan]} {2} $$

Kekuatan rata-rata dari sinyal yang didemodulasi adalah

$$ P_m = \ kiri (\ frac {A_cm \ kiri (t \ kanan)} {2 \ sqrt {2}} \ kanan) ^ 2 = \ frac {{A_ {c}} ^ {2} P} {8 } $$

Daya kebisingan rata-rata pada output adalah

$$ P_ {no} = \ frac {WN_0} {4} $$

Gantikan, nilai-nilai ini dalam output SNR rumus.

$$ \ left (SNR \ right) _ {O, DSBSC} = \ frac {Average \: \: Power \: \: of \: \: demodulated \: \: signal} {Average \: \: Power \: \: dari \: \: noise \: \: at \: \: Output} $$

$$ \ Rightarrow \ left (SNR \ right) _ {O, DSBSC} = \ left (\ frac {{A_ {c}} ^ {2} P} {8} \ kanan) / \ kiri (\ frac {WN_0 } {4} \ kanan) = \ frac {{A_ {c}} ^ {2} P} {2WN_0} $$

Gantikan, nilai dalam Figure of merit rumus penerima DSBSC.

$$ F = \ frac {\ kiri (SNR \ kanan) _ {O, DSBSC}} {\ kiri (SNR \ kanan) _ {C, DSBSC}} $$

$$ \ Rightarrow F = \ kiri (\ frac {{A_ {c}} ^ {2} P} {2WN_0} \ kanan) / \ kiri (\ frac {{A_ {c}} ^ {2} P} { 2WN_0} \ kanan) $$

$$ \ Rightarrow F = 1 $$

Oleh karena itu, Gambar manfaat penerima DSBSC adalah 1.

Perhitungan SNR dalam Sistem SSBSC

Pertimbangkan model penerima sistem SSBSC berikut untuk menganalisis kebisingan.

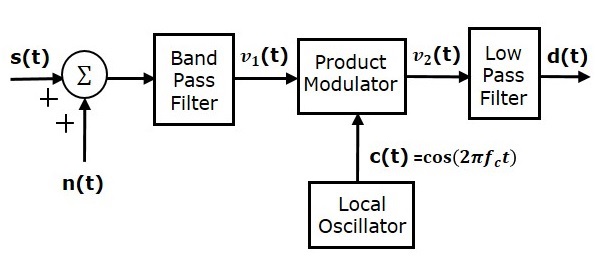
Kita tahu bahwa gelombang termodulasi SSBSC memiliki sideband yang lebih rendah

$$ s \ kiri (t \ kanan) = \ frac {A_mA_c} {2} \ cos \ kiri [2 \ pi \ kiri (f_c-f_m \ kanan) t \ kanan] $$

Daya rata-rata gelombang termodulasi SSBSC adalah

$$ P_s = \ left (\ frac {A_mA_c} {2 \ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8} $$

Daya rata-rata noise dalam bandwidth pesan adalah

$$ P_ {nc} = WN_0 $$

Gantikan, nilai-nilai ini dalam channel SNR rumus.

$$ \ left (SNR \ right) _ {C, SSBSC} = \ frac {Average \: \: Power \: \: of \: \: SSBSC \: \: modulated \: \: wave} {Rata-rata \: \: Power \: \: of \: \: noise \: \: in \: \: message \: \: bandwidth} $$

$$ \ Rightarrow \ left (SNR \ right) _ {C, SSBSC} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} $$

Asumsikan kebisingan band pass dicampur dengan gelombang termodulasi SSBSC di saluran seperti yang ditunjukkan pada gambar di atas. Kombinasi ini diterapkan sebagai salah satu masukan ke modulator produk. Oleh karena itu, input dari modulator produk ini adalah

$$ v_1 \ kiri (t \ kanan) = s \ kiri (t \ kanan) + n \ kiri (t \ kanan) $$

$$ v_1 \ kiri (t \ kanan) = \ frac {A_mA_c} {2} \ cos \ kiri [2 \ pi \ kiri (f_c-f_m \ kanan) t \ kanan] + n_I \ kiri (t \ kanan) \ cos \ left (2 \ pi f_ct \ right) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) $$

$$ v_2 \ kiri (t \ kanan) = v_1 \ kiri (t \ kanan) c \ kiri (t \ kanan) $$

Gantikan, nilai $ v_1 \ left (t \ right) $ dan $ c \ left (t \ right) $ dalam persamaan di atas.

$ \ Rightarrow v_2 (t) = (\ frac {A_mA_c} {2} \ cos [2 \ pi (f_c-f_m) t] + n_I (t) \ cos (2 \ pi f_ct) - $

$ n_Q (t) \ sin (2 \ pi f_ct)) \ cos (2 \ pi f_ct) $

$ \ Rightarrow v_2 \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] \ cos \ kiri (2 \ pi f_ct \ kanan) + $

$ n_I \ kiri (t \ kanan) \ cos ^ 2 \ kiri (2 \ pi f_ct \ kanan) -n_Q \ kiri (t \ kanan) \ sin \ kiri (2 \ pi f_ct \ kanan) \ cos \ kiri (2 \ pi f_ct \ kanan) $

$ \ Rightarrow v_2 \ left (t \ right) = \ frac {A_mA_c} {4} \ kiri \ {\ cos \ kiri [2 \ pi \ kiri (2f_c-f_m \ kanan) t \ kanan] + \ cos \ kiri (2 \ pi f_mt \ kanan) \ kanan \} + $

$ n_Saya \ kiri (t \ kanan) \ kiri (\ frac {1+ \ cos \ kiri (4 \ pi f_ct \ kanan)} {2} \ kanan) - n_Q \ kiri (t \ kanan) \ frac {\ sin \ kiri (4 \ pi f_ct \ kanan)} {2} $

Ketika sinyal di atas diaplikasikan sebagai input ke filter low pass, kita akan mendapatkan output dari filter low pass sebagai

$$ d \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left (2 \ pi f_mt \ right) + \ frac {n_I \ left (t \ right)} {2} $$

Kekuatan rata-rata dari sinyal yang didemodulasi adalah

$$ P_m = \ kiri (\ frac {A_mA_c} {4 \ sqrt {2}} \ kanan) ^ 2 = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {32} $$

Daya kebisingan rata-rata pada output adalah

$$ P_ {no} = \ frac {WN_0} {4} $$

Gantikan, nilai-nilai ini dalam output SNR rumus

$$ \ left (SNR \ right) _ {O, SSBSC} = \ frac {Average \: \: Power \: \: of \: \: demodulated \: \: signal} {Average \: \: Power \: \: dari \: \: noise \: \: at \: \: output} $$

$$ \ Rightarrow \ left (SNR \ right) _ {O, SSBSC} = \ left (\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {32} \ kanan ) / \ kiri (\ frac {WN_0} {4} \ kanan) = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} $$

Gantikan, nilai dalam Figure of merit rumus penerima SSBSC

$$ F = \ frac {\ kiri (SNR \ kanan) _ {O, SSBSC}} {\ kiri (SNR \ kanan) _ {C, SSBSC}} $$

$$ F = \ kiri (\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} \ kanan) / \ kiri (\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} \ kanan) $$

$$ F = 1 $$

Oleh karena itu, Gambar manfaat penerima SSBSC adalah 1.