Pengoptimalan Cembung - Panduan Cepat

Mata kuliah ini bermanfaat bagi mahasiswa yang ingin memecahkan masalah optimasi non linier yang muncul dalam berbagai aplikasi keteknikan dan keilmuan. Kursus ini dimulai dengan teori dasar pemrograman linier dan akan memperkenalkan konsep himpunan cembung dan fungsi serta terminologi terkait untuk menjelaskan berbagai teorema yang diperlukan untuk menyelesaikan masalah pemrograman non linier. Kursus ini akan memperkenalkan berbagai algoritma yang digunakan untuk menyelesaikan masalah tersebut. Jenis masalah ini muncul dalam berbagai aplikasi termasuk pembelajaran mesin, masalah pengoptimalan dalam teknik kelistrikan, dll. Hal ini menuntut siswa untuk memiliki pengetahuan sebelumnya tentang konsep matematika dan kalkulus sekolah menengah.

Dalam mata kuliah ini mahasiswa akan belajar memecahkan masalah optimasi seperti $min f\left ( x \right )$ tunduk pada beberapa kendala.

Masalah ini mudah dipecahkan jika berfungsi $f\left ( x \right )$adalah fungsi linier dan jika pembatasnya linier. Maka itu disebut masalah pemrograman linier (LPP). Tetapi jika batasannya non-linier, maka sulit untuk menyelesaikan masalah di atas. Kecuali jika kita dapat memplot fungsi dalam grafik, maka mencoba menganalisis optimasi bisa menjadi salah satu cara, tetapi kita tidak dapat memplot fungsi jika di luar tiga dimensi. Oleh karena itu, muncullah teknik pemrograman non-linier atau pemrograman cembung untuk menyelesaikan masalah tersebut. Dalam tutorial ini, kami akan fokus pada mempelajari teknik-teknik tersebut dan pada akhirnya, beberapa algoritma untuk menyelesaikan masalah tersebut. pertama kita akan membawa pengertian himpunan cembung yang merupakan dasar dari masalah pemrograman cembung. Kemudian dengan pengenalan fungsi cembung, kita akan membahas beberapa teorema penting untuk menyelesaikan masalah tersebut dan beberapa algoritma berdasarkan pada teorema tersebut.

Terminologi

• Ruang angkasa $\mathbb{R}^n$ - Ini adalah vektor berdimensi-n dengan bilangan real, didefinisikan sebagai berikut - $\mathbb{R}^n=\left \{ \left ( x_1,x_2,...,x_n \right )^{\tau }:x_1,x_2,....,x_n \in \mathbb{R} \right \}$

• Ruang angkasa $\mathbb{R}^{mXn}$ - Ini adalah satu set dari semua matriks nilai riil urutan $mXn$.

Metodologi

Pemrograman Linier juga disebut Pengoptimalan Linier, adalah teknik yang digunakan untuk menyelesaikan masalah matematika yang hubungannya bersifat linier. sifat dasar Linear Programming adalah untuk memaksimalkan atau meminimalkanobjective function dengan tunduk pada beberapa constraints. Fungsi obyektif merupakan fungsi linier yang didapat dari model matematika soal. Kendala adalah kondisi yang dikenakan pada model dan juga linier.

• Dari pertanyaan yang diberikan, temukan fungsi tujuan.
• temukan kendala.
• Gambarkan batasan pada grafik.
• temukan wilayah yang layak, yang dibentuk oleh persimpangan semua kendala.
• temukan simpul dari wilayah yang memungkinkan.
• temukan nilai dari fungsi tujuan pada simpul-simpul ini.
• Titik puncak yang memaksimalkan atau meminimalkan fungsi tujuan (menurut pertanyaan) adalah jawabannya.

Contoh

Step 1 - Maksimalkan $5x+3y$ tunduk pada

$x+y\leq 2$,

$3x+y\leq 3$,

$x\geq 0 \:and \:y\geq 0$

Solution -

Langkah pertama adalah menemukan wilayah yang layak pada grafik.

Jelas dari grafik, simpul dari daerah yang layak adalah

$\left ( 0, 0 \right )\left ( 0, 2 \right )\left ( 1, 0 \right )\left ( \frac{1}{2}, \frac{3}{2} \right )$

Membiarkan $f\left ( x, y \right )=5x+3y$

Menempatkan nilai-nilai ini dalam fungsi tujuan, kita dapatkan -

$f\left ( 0, 0 \right )$= 0

$f\left ( 0, 2 \right )$= 6

$f\left ( 1, 0 \right )$= 5

$f\left ( \frac{1}{2}, \frac{3}{2} \right )$= 7

Oleh karena itu, fungsinya dimaksimalkan pada $\left ( \frac{1}{2}, \frac{3}{2} \right )$

Step 2- Perusahaan jam tangan memproduksi jam tangan digital dan mekanis. Proyeksi jangka panjang menunjukkan permintaan yang diharapkan dari setidaknya 100 jam tangan digital dan 80 jam tangan mekanis setiap hari. Karena keterbatasan kapasitas produksi, tidak lebih dari 200 jam tangan digital dan 170 jam tangan mekanis dapat dibuat setiap hari. Untuk memenuhi kontrak pengiriman, total sedikitnya 200 jam tangan banyak dikirim setiap hari.

Jika setiap jam tangan digital yang terjual menghasilkan a $\$2$ loss, but each mechanical watch produces a $\$5$ laba, berapa banyak dari setiap jenis yang harus dibuat setiap hari untuk memaksimalkan laba bersih?

Solution -

Membiarkan $x$ menjadi jumlah jam tangan digital yang diproduksi

$y$ menjadi jumlah jam tangan mekanis yang diproduksi

Menurut pertanyaan, minimal 100 jam tangan digital harus dibuat setiap hari dan maksimal 200 jam tangan digital bisa dibuat.

$\Rightarrow 100 \leq \:x\leq 200$

Demikian pula, setidaknya 80 jam tangan mekanis harus dibuat setiap hari dan maksimum 170 jam tangan mekanis dapat dibuat.

$\Rightarrow 80 \leq \:y\leq 170$

Karena setidaknya 200 jam tangan akan diproduksi setiap hari.

$\Rightarrow x +y\leq 200$

Karena setiap jam tangan digital yang dijual menghasilkan a $\$2$ loss, but each mechanical watch produces a $\$5$ keuntungan,

Keuntungan total dapat dihitung sebagai

$Profit =-2x + 5y$

Dan kita harus memaksimalkan keuntungan, Oleh karena itu, pertanyaannya dapat dirumuskan sebagai -

Maksimalkan $-2x + 5y$ tunduk pada

$100 \:\leq x\:\leq 200$

$80 \:\leq y\:\leq 170$

$x+y\:\leq 200$

Merencanakan persamaan di atas dalam grafik, kita dapatkan,

Simpul dari wilayah yang layak adalah

$\left ( 100, 170\right )\left ( 200, 170\right )\left ( 200, 180\right )\left ( 120, 80\right ) and \left ( 100, 100\right )$

Nilai maksimum dari fungsi tujuan diperoleh di $\left ( 100, 170\right )$ Sehingga, untuk memaksimalkan keuntungan bersih, harus diproduksi 100 unit jam tangan digital dan 170 unit jam tangan mekanik.

Norma adalah fungsi yang memberikan nilai yang sangat positif ke vektor atau variabel.

Norma adalah sebuah fungsi $f:\mathbb{R}^n\rightarrow \mathbb{R}$

Karakteristik dasar dari suatu norma adalah -

Membiarkan $X$ menjadi vektor seperti itu $X\in \mathbb{R}^n$

• $\left \| x \right \|\geq 0$

• $\left \| x \right \|= 0 \Leftrightarrow x= 0\forall x \in X$

• $\left \|\alpha x \right \|=\left | \alpha \right |\left \| x \right \|\forall \:x \in X and \:\alpha \:is \:a \:scalar$

• $\left \| x+y \right \|\leq \left \| x \right \|+\left \| y \right \| \forall x,y \in X$

• $\left \| x-y \right \|\geq \left \| \left \| x \right \|-\left \| y \right \| \right \|$

Menurut definisi, norma dihitung sebagai berikut -

• $\left \| x \right \|_1=\displaystyle\sum\limits_{i=1}^n\left | x_i \right |$

• $\left \| x \right \|_2=\left ( \displaystyle\sum\limits_{i=1}^n\left | x_i \right |^2 \right )^{\frac{1}{2}}$

• $\left \| x \right \|_p=\left ( \displaystyle\sum\limits_{i=1}^n\left | x_i \right |^p \right )^{\frac{1}{p}},1 \leq p \leq \infty$

Norma adalah fungsi berkelanjutan.

Bukti

Menurut definisi, jika $x_n\rightarrow x$ di $X\Rightarrow f\left ( x_n \right )\rightarrow f\left ( x \right ) $ kemudian $f\left ( x \right )$ adalah fungsi konstan.

Membiarkan $f\left ( x \right )=\left \| x \right \|$

Karena itu, $\left | f\left ( x_n \right )-f\left ( x \right ) \right |=\left | \left \| x_n \right \| -\left \| x \right \|\right |\leq \left | \left | x_n-x \right | \:\right |$

Sejak $x_n \rightarrow x$ jadi, $\left \| x_n-x \right \|\rightarrow 0$

Karena itu $\left | f\left ( x_n \right )-f\left ( x \right ) \right |\leq 0\Rightarrow \left | f\left ( x_n \right )-f\left ( x \right ) \right |=0\Rightarrow f\left ( x_n \right )\rightarrow f\left ( x \right )$

Oleh karena itu, norma merupakan fungsi yang berkelanjutan.

Hasil kali dalam adalah fungsi yang memberikan skalar pada sepasang vektor.

Produk Batin - $f:\mathbb{R}^n \times \mathbb{R}^n\rightarrow \kappa$ dimana $\kappa$ adalah skalar.

Karakteristik dasar produk dalam adalah sebagai berikut -

Membiarkan $X \in \mathbb{R}^n$

• $\left \langle x,x \right \rangle\geq 0, \forall x \in X$

• $\left \langle x,x \right \rangle=0\Leftrightarrow x=0, \forall x \in X$

• $\left \langle \alpha x,y \right \rangle=\alpha \left \langle x,y \right \rangle,\forall \alpha \in \kappa \: and\: \forall x,y \in X$

• $\left \langle x+y,z \right \rangle =\left \langle x,z \right \rangle +\left \langle y,z \right \rangle, \forall x,y,z \in X$

• $\left \langle \overline{y,x} \right \rangle=\left ( x,y \right ), \forall x, y \in X$

Note -

• Hubungan antara norma dan produk dalam: $\left \| x \right \|=\sqrt{\left ( x,x \right )}$

• $\forall x,y \in \mathbb{R}^n,\left \langle x,y \right \rangle=x_1y_1+x_2y_2+...+x_ny_n$

Contoh

1. temukan produk dalam dari $x=\left ( 1,2,1 \right )\: and \: y=\left ( 3,-1,3 \right )$

Larutan

$\left \langle x,y \right \rangle =x_1y_1+x_2y_2+x_3y_3$

$\left \langle x,y \right \rangle=\left ( 1\times3 \right )+\left ( 2\times-1 \right )+\left ( 1\times3 \right )$

$\left \langle x,y \right \rangle=3+\left ( -2 \right )+3$

$\left \langle x,y \right \rangle=4$

2. Jika $x=\left ( 4,9,1 \right ),y=\left ( -3,5,1 \right )$ dan $z=\left ( 2,4,1 \right )$, Temukan $\left ( x+y,z \right )$

Larutan

Seperti yang kita tahu, $\left \langle x+y,z \right \rangle=\left \langle x,z \right \rangle+\left \langle y,z \right \rangle$

$\left \langle x+y,z \right \rangle=\left ( x_1z_1+x_2z_2+x_3z_3 \right )+\left ( y_1z_1+y_2z_2+y_3z_3 \right )$

$\left \langle x+y,z \right \rangle=\left \{ \left ( 4\times 2 \right )+\left ( 9\times 4 \right )+\left ( 1\times1 \right ) \right \}+$

$\left \{ \left ( -3\times2 \right )+\left ( 5\times4 \right )+\left ( 1\times 1\right ) \right \}$

$\left \langle x+y,z \right \rangle=\left ( 8+36+1 \right )+\left ( -6+20+1 \right )$

$\left \langle x+y,z \right \rangle=45+15$

$\left \langle x+y,z \right \rangle=60$

Minima Lokal atau Minimalkan

$\bar{x}\in \:S$ dikatakan sebagai minimum lokal suatu fungsi $f$ jika $f\left ( \bar{x} \right )\leq f\left ( x \right ),\forall x \in N_\varepsilon \left ( \bar{x} \right )$ dimana $N_\varepsilon \left ( \bar{x} \right )$ Berarti lingkungan $\bar{x}$, yaitu, $N_\varepsilon \left ( \bar{x} \right )$berarti $ \ kiri \ | x- \ bar {x} \ kanan \ | <\ varepsilon $

Maxima atau Maximizer Lokal

$\bar{x}\in \:S$ dikatakan sebagai maksima lokal suatu fungsi $f$ jika $f\left ( \bar{x} \right )\geq f\left ( x \right ), \forall x \in N_\varepsilon \left ( \bar{x} \right )$ dimana $N_\varepsilon \left ( \bar{x} \right )$ Berarti lingkungan $\bar{x}$, yaitu, $N_\varepsilon \left ( \bar{x} \right )$berarti $ \ kiri \ | x- \ bar {x} \ kanan \ | <\ varepsilon $

Minimum global

$\bar{x}\in \:S$ dikatakan sebagai minimum global suatu fungsi $f$ jika $f\left ( \bar{x} \right )\leq f\left ( x \right ), \forall x \in S$

Maksimal global

$\bar{x}\in \:S$ dikatakan sebagai maksima global suatu fungsi $f$ jika $f\left ( \bar{x} \right )\geq f\left ( x \right ), \forall x \in S$

Contoh

Step 1 - temukan nilai minimum dan maksimum lokal $f\left ( \bar{x} \right )=\left | x^2-4 \right |$

Solution -

Dari grafik fungsi di atas, terlihat jelas bahwa local minima terjadi pada $x= \pm 2$ dan maksima lokal pada $x = 0$

Step 2 - temukan minimum global dari fungsinya $f\left (x \right )=\left | 4x^3-3x^2+7 \right |$

Solution -

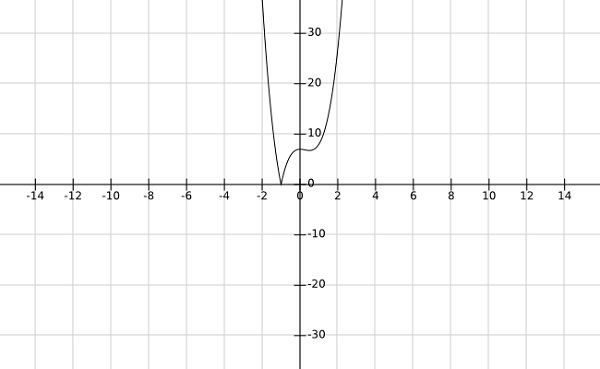
Dari grafik fungsi di atas, terlihat jelas bahwa global minima terjadi pada $x=-1$.

Membiarkan $S\subseteq \mathbb{R}^n$ Himpunan S dikatakan cembung jika ruas garis yang menghubungkan dua titik dari himpunan S juga dimiliki oleh S, yaitu jika $x_1,x_2 \in S$, kemudian $\lambda x_1+\left ( 1-\lambda \right )x_2 \in S$ dimana $\lambda \in\left ( 0,1 \right )$.

Note -

• Penyatuan dua set cembung bisa jadi cembung atau mungkin juga tidak.
• Perpotongan dua himpunan cembung selalu cembung.

Proof

Membiarkan $S_1$ dan $S_2$ menjadi dua set cembung.

Membiarkan $S_3=S_1 \cap S_2$

Membiarkan $x_1,x_2 \in S_3$

Sejak $S_3=S_1 \cap S_2$ jadi $x_1,x_2 \in S_1$dan $x_1,x_2 \in S_2$

Sejak $S_i$ adalah himpunan cembung, $\forall$ $i \in 1,2,$

Jadi $\lambda x_1+\left ( 1-\lambda \right )x_2 \in S_i$ dimana $\lambda \in \left ( 0,1 \right )$

Oleh karena itu, $\lambda x_1+\left ( 1-\lambda \right )x_2 \in S_1\cap S_2$

$\Rightarrow \lambda x_1+\left ( 1-\lambda \right )x_2 \in S_3$

Karenanya, $S_3$ adalah satu set cembung.

• Rata-rata tertimbang formulir $\displaystyle\sum\limits_{i=1}^k \lambda_ix_i$,dimana $\displaystyle\sum\limits_{i=1}^k \lambda_i=1$ dan $\lambda_i\geq 0,\forall i \in \left [ 1,k \right ]$ disebut kombinasi kerucut dari $x_1,x_2,....x_k.$

• Rata-rata tertimbang formulir $\displaystyle\sum\limits_{i=1}^k \lambda_ix_i$, dimana $\displaystyle\sum\limits_{i=1}^k \lambda_i=1$ disebut kombinasi affine $x_1,x_2,....x_k.$

• Rata-rata tertimbang formulir $\displaystyle\sum\limits_{i=1}^k \lambda_ix_i$ disebut kombinasi linier $x_1,x_2,....x_k.$

Contoh

Step 1 - Buktikan bahwa set $S=\left \{ x \in \mathbb{R}^n:Cx\leq \alpha \right \}$ adalah satu set cembung.

Larutan

Membiarkan $x_1$ dan $x_2 \in S$

$\Rightarrow Cx_1\leq \alpha$ dan $\:and \:Cx_2\leq \alpha$

Memperlihatkan:$\:\:y=\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\in S \:\forall \:\lambda \in\left ( 0,1 \right )$

$Cy=C\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )=\lambda Cx_1+\left ( 1-\lambda \right )Cx_2$

$\Rightarrow Cy\leq \lambda \alpha+\left ( 1-\lambda \right )\alpha$

$\Rightarrow Cy\leq \alpha$

$\Rightarrow y\in S$

Karena itu, $S$ adalah satu set cembung.

Step 2 - Buktikan bahwa set $S=\left \{ \left ( x_1,x_2 \right )\in \mathbb{R}^2:x_{1}^{2}\leq 8x_2 \right \}$ adalah satu set cembung.

Larutan

Membiarkan $x,y \in S$

Membiarkan $x=\left ( x_1,x_2 \right )$ dan $y=\left ( y_1,y_2 \right )$

$\Rightarrow x_{1}^{2}\leq 8x_2$ dan $y_{1}^{2}\leq 8y_2$

Untuk menunjukkan - $\lambda x+\left ( 1-\lambda \right )y\in S\Rightarrow \lambda \left ( x_1,x_2 \right )+\left (1-\lambda \right )\left ( y_1,y_2 \right ) \in S\Rightarrow \left [ \lambda x_1+\left ( 1- \lambda)y_2] \in S\right ) \right ]$

$Now, \left [\lambda x_1+\left ( 1-\lambda \right )y_1 \right ]^{2}=\lambda ^2x_{1}^{2}+\left ( 1-\lambda \right )^2y_{1}^{2}+2 \lambda\left ( 1-\lambda \right )x_1y_1$

Tapi $2x_1y_1\leq x_{1}^{2}+y_{1}^{2}$

Karena itu,

$\left [ \lambda x_1 +\left ( 1-\lambda \right )y_1\right ]^{2}\leq \lambda ^2x_{1}^{2}+\left ( 1- \lambda \right )^2y_{1}^{2}+2 \lambda\left ( 1- \lambda \right )\left ( x_{1}^{2}+y_{1}^{2} \right )$

$\Rightarrow \left [ \lambda x_1+\left ( 1-\lambda \right )y_1 \right ]^{2}\leq \lambda x_{1}^{2}+\left ( 1- \lambda \right )y_{1}^{2}$

$\Rightarrow \left [ \lambda x_1+\left ( 1-\lambda \right )y_1 \right ]^{2}\leq 8\lambda x_2+8\left ( 1- \lambda \right )y_2$

$\Rightarrow \left [ \lambda x_1+\left ( 1-\lambda \right )y_1 \right ]^{2}\leq 8\left [\lambda x_2+\left ( 1- \lambda \right )y_2 \right ]$

$\Rightarrow \lambda x+\left ( 1- \lambda \right )y \in S$

Step 3 - Tunjukkan satu set $S \in \mathbb{R}^n$ adalah konveks jika dan hanya jika untuk setiap bilangan bulat k, setiap kombinasi konveks dari setiap titik k $S$ masuk $S$.

Larutan

Membiarkan $S$menjadi satu set cembung. kemudian, untuk menunjukkan;

$c_1x_1+c_2x_2+.....+c_kx_k \in S, \displaystyle\sum\limits_{1}^k c_i=1,c_i\geq 0, \forall i \in 1,2,....,k$

Bukti dengan induksi

Untuk $k=1,x_1 \in S, c_1=1 \Rightarrow c_1x_1 \in S$

Untuk $k=2,x_1,x_2 \in S, c_1+c_2=1$ dan Karena S adalah himpunan cembung

$\Rightarrow c_1x_1+c_2x_2 \in S.$

Misalkan kombinasi cembung dari m titik S ada di S yaitu,

$c_1x_1+c_2x_2+...+c_mx_m \in S,\displaystyle\sum\limits_{1}^m c_i=1 ,c_i \geq 0, \forall i \in 1,2,...,m$

Sekarang, Biarkan $x_1,x_2....,x_m,x_{m+1} \in S$

Membiarkan $x=\mu_1x_1+\mu_2x_2+...+\mu_mx_m+\mu_{m+1}x_{m+1}$

Membiarkan $x=\left ( \mu_1+\mu_2+...+\mu_m \right )\frac{\mu_1x_1+\mu_2x_2+\mu_mx_m}{\mu_1+\mu_2+.........+\mu_m}+\mu_{m+1}x_{m+1}$

Membiarkan $y=\frac{\mu_1x_1+\mu_2x_2+...+\mu_mx_m}{\mu_1+\mu_2+.........+\mu_m}$

$\Rightarrow x=\left ( \mu_1+\mu_2+...+\mu_m \right )y+\mu_{m+1}x_{m+1}$

Sekarang $y \in S$ karena jumlah koefisiennya adalah 1.

$\Rightarrow x \in S$ karena S adalah himpunan cembung dan $y,x_{m+1} \in S$

Karenanya dibuktikan dengan induksi.

Satu set $A$ dikatakan sebagai himpunan affine jika untuk dua titik yang berbeda, garis yang melewati titik-titik ini terletak di himpunan $A$.

Note -

• $S$ adalah himpunan affine jika dan hanya jika ia berisi setiap kombinasi affine dari poinnya.

• Himpunan kosong dan tunggal merupakan himpunan affine dan cembung.

  Misalnya, solusi persamaan linier adalah himpunan affine.

Bukti

Misalkan S adalah solusi dari persamaan linier.

Menurut definisi, $S=\left \{ x \in \mathbb{R}^n:Ax=b \right \}$

Membiarkan $x_1,x_2 \in S\Rightarrow Ax_1=b$ dan $Ax_2=b$

Untuk membuktikan : $A\left [ \theta x_1+\left ( 1-\theta \right )x_2 \right ]=b, \forall \theta \in\left ( 0,1 \right )$

$A\left [ \theta x_1+\left ( 1-\theta \right )x_2 \right ]=\theta Ax_1+\left ( 1-\theta \right )Ax_2=\theta b+\left ( 1-\theta \right )b=b$

Jadi S adalah himpunan affine.

Dalil

Jika $C$ adalah satu set affine dan $x_0 \in C$, lalu set $V= C-x_0=\left \{ x-x_0:x \in C \right \}$ adalah subruang dari C.

Bukti

Membiarkan $x_1,x_2 \in V$

Memperlihatkan: $\alpha x_1+\beta x_2 \in V$ untuk beberapa $\alpha,\beta$

Sekarang, $x_1+x_0 \in C$ dan $x_2+x_0 \in C$ menurut definisi V

Sekarang, $\alpha x_1+\beta x_2+x_0=\alpha \left ( x_1+x_0 \right )+\beta \left ( x_2+x_0 \right )+\left ( 1-\alpha -\beta \right )x_0$

Tapi $\alpha \left ( x_1+x_0 \right )+\beta \left ( x_2+x_0 \right )+\left ( 1-\alpha -\beta \right )x_0 \in C$ karena C adalah himpunan affine.

Karena itu, $\alpha x_1+\beta x_2 \in V$

Karenanya terbukti.

Lambung cembung dari sekumpulan titik di S adalah batas dari wilayah cembung terkecil yang berisi semua titik S di dalamnya atau di batasnya.

ATAU

Membiarkan $S\subseteq \mathbb{R}^n$ Cembung lambung S, dilambangkan $Co\left ( S \right )$ oleh adalah kumpulan dari semua kombinasi cembung S, yaitu, $x \in Co\left ( S \right )$ jika dan hanya jika $x \in \displaystyle\sum\limits_{i=1}^n \lambda_ix_i$, dimana $\displaystyle\sum\limits_{1}^n \lambda_i=1$ dan $\lambda_i \geq 0 \forall x_i \in S$

Remark - Conves hull dari sekumpulan titik di S pada bidang mendefinisikan poligon cembung dan titik S pada batas poligon mendefinisikan simpul dari poligon.

Theorem $Co\left ( S \right )= \left \{ x:x=\displaystyle\sum\limits_{i=1}^n \lambda_ix_i,x_i \in S, \displaystyle\sum\limits_{i=1}^n \lambda_i=1,\lambda_i \geq 0 \right \}$ Tunjukkan bahwa lambung cembung adalah himpunan cembung.

Bukti

Membiarkan $x_1,x_2 \in Co\left ( S \right )$, kemudian $x_1=\displaystyle\sum\limits_{i=1}^n \lambda_ix_i$ dan $x_2=\displaystyle\sum\limits_{i=1}^n \lambda_\gamma x_i$ dimana $\displaystyle\sum\limits_{i=1}^n \lambda_i=1, \lambda_i\geq 0$ dan $\displaystyle\sum\limits_{i=1}^n \gamma_i=1,\gamma_i\geq0$

Untuk $\theta \in \left ( 0,1 \right ),\theta x_1+\left ( 1-\theta \right )x_2=\theta \displaystyle\sum\limits_{i=1}^n \lambda_ix_i+\left ( 1-\theta \right )\displaystyle\sum\limits_{i=1}^n \gamma_ix_i$

$\theta x_1+\left ( 1-\theta \right )x_2=\displaystyle\sum\limits_{i=1}^n \lambda_i \theta x_i+\displaystyle\sum\limits_{i=1}^n \gamma_i\left ( 1-\theta \right )x_i$

$\theta x_1+\left ( 1-\theta \right )x_2=\displaystyle\sum\limits_{i=1}^n\left [ \lambda_i\theta +\gamma_i\left ( 1-\theta \right ) \right ]x_i$

Mempertimbangkan koefisien,

$\displaystyle\sum\limits_{i=1}^n\left [ \lambda_i\theta +\gamma_i\left ( 1-\theta \right ) \right ]=\theta \displaystyle\sum\limits_{i=1}^n \lambda_i+\left ( 1-\theta \right )\displaystyle\sum\limits_{i=1}^n\gamma_i=\theta +\left ( 1-\theta \right )=1$

Karenanya, $\theta x_1+\left ( 1-\theta \right )x_2 \in Co\left ( S \right )$

Jadi, lambung cembung adalah himpunan cembung.

Misalkan S menjadi himpunan sewenang-wenang $\mathbb{R}^n$.Jika $x \in Co\left ( S \right )$, kemudian $x \in Co\left ( x_1,x_2,....,x_n,x_{n+1} \right )$.

Bukti

Sejak $x \in Co\left ( S\right )$, kemudian $x$ diwakili oleh kombinasi cembung dari sejumlah titik terbatas di S, yaitu,

$x=\displaystyle\sum\limits_{j=1}^k \lambda_jx_j,\displaystyle\sum\limits_{j=1}^k \lambda_j=1, \lambda_j \geq 0$ dan $x_j \in S, \forall j \in \left ( 1,k \right )$

Jika $k \leq n+1$, hasil yang didapat jelas benar.

Jika $k \geq n+1$, kemudian $\left ( x_2-x_1 \right )\left ( x_3-x_1 \right ),....., \left ( x_k-x_1 \right )$ bergantung secara linier.

$\Rightarrow \exists \mu _j \in \mathbb{R}, 2\leq j\leq k$ (tidak semuanya nol) seperti itu $\displaystyle\sum\limits_{j=2}^k \mu _j\left ( x_j-x_1 \right )=0$

Menetapkan $\mu_1=-\displaystyle\sum\limits_{j=2}^k \mu _j$, kemudian $\displaystyle\sum\limits_{j=1}^k \mu_j x_j=0, \displaystyle\sum\limits_{j=1}^k \mu_j=0$

dimana tidak semuanya $\mu_j's$sama dengan nol. Sejak$\displaystyle\sum\limits_{j=1}^k \mu_j=0$, setidaknya satu dari $\mu_j > 0,1 \leq j \leq k$

Kemudian, $x=\displaystyle\sum\limits_{1}^k \lambda_j x_j+0$

$x=\displaystyle\sum\limits_{1}^k \lambda_j x_j- \alpha \displaystyle\sum\limits_{1}^k \mu_j x_j$

$x=\displaystyle\sum\limits_{1}^k\left ( \lambda_j- \alpha\mu_j \right )x_j $

Memilih $\alpha$ seperti yang $\alpha=min\left \{ \frac{\lambda_j}{\mu_j}, \mu_j\geq 0 \right \}=\frac{\lambda_j}{\mu _j},$ untuk beberapa $i=1,2,...,k$

Jika $\mu_j\leq 0, \lambda_j-\alpha \mu_j\geq 0$

Jika $\mu_j> 0, then \:\frac{\lambda _j}{\mu_j}\geq \frac{\lambda_i}{\mu _i}=\alpha \Rightarrow \lambda_j-\alpha \mu_j\geq 0, j=1,2,...k$

Khususnya, $\lambda_i-\alpha \mu_i=0$, menurut definisi $\alpha$

$x=\displaystyle\sum\limits_{j=1}^k \left ( \lambda_j- \alpha\mu_j\right )x_j$,dimana

$\lambda_j- \alpha\mu_j\geq0$ dan $\displaystyle\sum\limits_{j=1}^k\left ( \lambda_j- \alpha\mu_j\right )=1$ dan $\lambda_i- \alpha\mu_i=0$

Jadi, x dapat direpresentasikan sebagai kombinasi cembung dari paling banyak (k-1) titik.

Proses reduksi ini dapat diulang sampai x direpresentasikan sebagai kombinasi cembung dari elemen (n + 1).

Misalkan S menjadi himpunan tidak kosong, tertutup dan dibatasi (juga disebut himpunan kompak) di $\mathbb{R}^n$ dan biarkan $f:S\rightarrow \mathbb{R} $ menjadi fungsi kontinu pada S, maka masalah min $\left \{ f\left ( x \right ):x \in S \right \}$ mencapai minimumnya.

Bukti

Karena S tidak kosong dan dibatasi, maka terdapat batas bawah.

$\alpha =Inf\left \{ f\left ( x \right ):x \in S \right \}$

Sekarang biarkan $S_j=\left \{ x \in S:\alpha \leq f\left ( x \right ) \leq \alpha +\delta ^j\right \} \forall j=1,2,...$ dan $\delta \in \left ( 0,1 \right )$

Menurut definisi infimium, $S_j$ tidak kosong, untuk masing-masing $j$.

Pilih beberapa $x_j \in S_j$ untuk mendapatkan urutan $\left \{ x_j \right \}$ untuk $j=1,2,...$

Karena S dibatasi, urutannya juga dibatasi dan ada urutan konvergen $\left \{ y_j \right \}$, yang menyatu dengan $\hat{x}$. Karenanya$\hat{x}$ adalah titik batas dan S ditutup, oleh karena itu, $\hat{x} \in S$. Karena f kontinu,$f\left ( y_i \right )\rightarrow f\left ( \hat{x} \right )$.

Sejak $\alpha \leq f\left ( y_i \right )\leq \alpha+\delta^k, \alpha=\displaystyle\lim_{k\rightarrow \infty}f\left ( y_i \right )=f\left ( \hat{x} \right )$

Jadi, $\hat{x}$ adalah solusi meminimalkan.

Catatan

Ada dua kondisi penting yang perlu dipegang Teorema Weierstrass. Ini adalah sebagai berikut -

• Step 1 - Himpunan S haruslah himpunan berbatas.

  Pertimbangkan fungsi f \ left (x \ right) = x $.

  Ini adalah himpunan tidak terbatas dan memiliki nilai minimum di setiap titik dalam domainnya.

  Jadi, untuk mendapatkan minimum, S harus dibatasi.

• Step 2 - Set S harus ditutup.

  Pertimbangkan fungsi $ f \ left (x \ right) = \ frac {1} {x} $ di domain \ left (0,1 \ right).

  Fungsi ini tidak ditutup dalam domain yang diberikan dan minimumnya juga tidak ada.

  Oleh karena itu, untuk mendapatkan minimum, S harus ditutup.

Misalkan S adalah cembung tertutup tidak kosong yang ditetapkan dalam $ \ mathbb {R} ^ n$ and let $t \ notin S$, then $\ ada$ a point $\ bar {x} \ dalam S$ with minimum distance from y, i.e.,$\ kiri \ | y- \ bar {x} \ kanan \ | \ leq \ kiri \ | yx \ kanan \ | \ forall x \ in S. $

Selanjutnya, $ \ bar {x}$ is a minimizing point if and only if $\ kiri (y- \ topi {x} \ kanan) ^ {T} \ kiri (x- \ topi {x} \ kanan) \ leq 0$ or $\ kiri (y- \ topi {x}, x- \ topi {x} \ kanan) \ leq 0 $

Bukti

Keberadaan titik terdekat

Sejak $ S \ ne \ phi, \ ada$ a point $\ hat {x} \ in S$ such that the minimum distance of S from y is less than or equal to $\ kiri \ | y- \ topi {x} \ kanan \ | $.

Tentukan $ \ hat {S} = S \ cap \ left \ {x: \ left \ | yx \ kanan \ | \ leq \ kiri \ | y- \ topi {x} \ kanan \ | \ kanan \} $

Sejak $ \ hat {S}$ is closed and bounded, and since norm is a continuous function, then by Weierstrass theorem, there exists a minimum point $\ hat {x} \ in S$ such that $\ kiri \ | y- \ topi {x} \ kanan \ | = Inf \ kiri \ {\ kiri \ | yx \ kanan \ |, x \ dalam S \ kanan \} $

Keunikan

Misalkan $ \ bar {x} \ dalam S$ such that $\ kiri \ | y- \ topi {x} \ kanan \ | = \ kiri \ | y- \ topi {x} \ kanan \ | = \ alpha $

Karena S cembung, $ \ frac {\ hat {x} + \ bar {x}} {2} \ in S $

Tapi, $ \ kiri \ | y- \ frac {\ topi {x} - \ bar {x}} {2} \ kanan \ | \ leq \ frac {1} {2} \ kiri \ | y- \ topi {x} \ kanan \ | + \ frac {1} {2} \ kiri \ | y- \ bar {x} \ kanan \ | = \ alpha $

Ini tidak bisa menjadi ketimpangan yang tegas karena $ \ hat {x} $ paling dekat dengan y.

Oleh karena itu, $ \ kiri \ | y- \ topi {x} \ kanan \ | = \ mu \ kiri \ | y- \ topi {x} \ kanan \ |$, for some $\ mu $

Sekarang $ \ kiri \ | \ mu \ kanan \ | = 1.$ If $\ mu = -1$, then $\ kiri (y- \ topi {x} \ kanan) = - \ kiri (y- \ topi {x} \ kanan) \ Kananarrow y = \ frac {\ hat {x} + \ bar {x}} {2} \ dalam S $

Tapi $ y \ dalam S$. Hence contradiction. Thus $\ mu = 1 \ Rightarrow \ hat {x} = \ bar {x} $

Jadi, meminimalkan poin itu unik.

Untuk bagian kedua pembuktian, asumsikan $ \ left (y- \ hat {x} \ right) ^ {\ tau} \ left (x- \ bar {x} \ right) \ leq 0$ for all $x \ dalam S $

Sekarang,

$ \ kiri \ | yx \ right \ | ^ {2} = \ kiri \ | y- \ topi {x} + \ topi {x} -x \ kanan \ | ^ {2} = \ kiri \ | y- \ topi {x} \ kanan \ | ^ {2} + \ kiri \ | \ topi {x} -x \ kanan \ | ^ {2} +2 \ kiri (\ topi {x} -x \ kanan) ^ {\ tau} \ kiri (y- \ topi {x} \ kanan) $

$ \ Rightarrow \ kiri \ | yx \ kanan \ | ^ {2} \ geq \ kiri \ | y- \ topi {x} \ kanan \ | ^ {2}$ because $\ kiri \ | \ hat {x} -x \ right \ | ^ {2} \ geq 0$ and $\ kiri (\ topi {x} - x \ kanan) ^ {T} \ kiri (y- \ topi {x} \ kanan) \ geq 0 $

Jadi, $ \ hat {x} $ meminimalkan poin.

Sebaliknya, asumsikan $ \ hat {x} $ adalah poin minimizimg.

$ \ Rightarrow \ kiri \ | yx \ kanan \ | ^ {2} \ geq \ kiri \ | y- \ hat {x} \ right \ | ^ 2 \ forall x \ in S $

Karena S adalah himpunan cembung.

$ \ Rightarrow \ lambda x + \ left (1- \ lambda \ right) \ hat {x} = \ hat {x} + \ lambda \ left (x- \ hat {x} \ kanan) \ dalam S$ for $x \ dalam S$ and $\ lambda \ in \ left (0,1 \ kanan) $

Sekarang, $ \ kiri \ | y- \ topi {x} - \ lambda \ kiri (x- \ topi {x} \ kanan) \ kanan \ | ^ {2} \ geq \ kiri \ | y- \ topi {x} \ kanan \ | ^ 2 $

Dan

$ \ kiri \ | y- \ topi {x} - \ lambda \ kiri (x- \ topi {x} \ kanan) \ kanan \ | ^ {2} = \ kiri \ | y- \ topi {x} \ kanan \ | ^ {2} + \ lambda ^ 2 \ kiri \ | x- \ topi {x} \ kanan \ | ^ {2} -2 \ lambda \ kiri (y- \ topi {x} \ kanan) ^ {T} \ kiri (x- \ hat {x} \ kanan) $

$ \ Rightarrow \ kiri \ | y- \ topi {x} \ kanan \ | ^ {2} + \ lambda ^ {2} \ kiri \ | x- \ topi {x} \ kanan \ | -2 \ lambda \ kiri (y- \ topi {x} \ kanan) ^ {T} \ kiri (x- \ topi {x} \ kanan) \ geq \ kiri \ | y- \ topi {x} \ kanan \ | ^ {2} $

$ \ Rightarrow 2 \ lambda \ left (y- \ hat {x} \ kanan) ^ {T} \ left (x- \ hat {x} \ kanan) \ leq \ lambda ^ 2 \ left \ | x- \ topi {x} \ kanan \ | ^ 2 $

$ \ Rightarrow \ left (y- \ hat {x} \ right) ^ {T} \ left (x- \ hat {x} \ kanan) \ leq 0 $

Oleh karena itu Terbukti.

Misalkan S adalah cembung tertutup yang tidak kosong yang ditetapkan di $ \ mathbb {R} ^ n$ and $t \ notin S$. Then, there exists a non zero vector $p$ and scalar $\ beta$ such that $p ^ T y> \ beta$ and $p ^ T x <\ beta$ for each $x \ dalam S $

Bukti

Karena S tidak kosong, himpunan cembung tertutup dan $ y \ notin S$ thus by closest point theorem, there exists a unique minimizing point $\ hat {x} \ dalam S $ sedemikian rupa

$ \ kiri (x- \ topi {x} \ kanan) ^ T \ kiri (y- \ topi {x} \ kanan) \ leq 0 \ depan x \ dalam S $

Misalkan $ p = \ left (y- \ hat {x} \ right) \ neq 0$ and $\ beta = \ topi {x} ^ T \ kiri (y- \ topi {x} \ kanan) = p ^ T \ hat {x} $.

Lalu $ \ kiri (x- \ topi {x} \ kanan) ^ T \ kiri (y- \ topi {x} \ kanan) \ leq 0 $

$ \ Rightarrow \ left (y- \ hat {x} \ right) ^ T \ left (x- \ hat {x} \ kanan) \ leq 0 $

$ \ Rightarrow \ left (y- \ hat {x} \ right) ^ Tx \ leq \ left (y- \ hat {x} \ kanan) ^ T \ hat {x} = \ hat {x} ^ T \ kiri (y- \ hat {x} \ kanan)$ i,e., $p ^ Tx \ leq \ beta $

Juga, $ p ^ Ty- \ beta = \ left (y- \ hat {x} \ right) ^ Ty- \ hat {x} ^ T \ left (y- \ hat {x} \ kanan) $

$ = \ kiri (y- \ topi {x} \ kanan) ^ T \ kiri (yx \ kanan) = \ kiri \ | y- \ topi {x} \ kanan \ | ^ {2}> 0 $

$ \ Rightarrow p ^ Ty> \ beta $

Teorema ini menghasilkan pemisahan hyperplanes. Hyperplanes berdasarkan teorema di atas dapat didefinisikan sebagai berikut -

Biarkan $ S_1$ and $S_2$ are be non-empty subsets of $\ mathbb {R}$ and $H = \ left \ {X: A ^ TX = b \ right \} $ menjadi hyperplane.

• Hyperplane H dikatakan memisahkan $ S_1$ and $S_2$ if $A ^ TX \ leq b \ untuk semua X \ di S_1$ and $A_TX \ geq b \ untuk semua X \ dalam S_2 $

• Hyperplane H dikatakan memisahkan $ S_1 secara ketat$ and $S_2$ if $A ^ TX <b \ untuk semua X \ di S_1$ and $A_TX> b \ untuk semua X \ dalam S_2 $

• Hyperplane H dikatakan memisahkan $ S_1 dengan kuat$ and $S_2$ if $A ^ TX \ leq b \ untuk semua X \ di S_1$ and $A_TX \ geq b + \ varepsilon \ untuk semua X \ di S_2$, where $\ varepsilon $ adalah skalar positif.

Himpunan C yang tidak kosong di $ \ mathbb {R} ^ n$ is said to be cone with vertex 0 if $x \ di C \ Rightarrow \ lambda x \ di C \ forall \ lambda \ geq 0 $.

Himpunan C adalah kerucut cembung jika ia cembung dan juga kerucut.

Misalnya, $ y = \ kiri | x \ right | $ bukan kerucut cembung karena bukan cembung.

Tapi, $ y \ geq \ kiri | x \ kanan | $ adalah kerucut cembung karena bentuknya cembung dan juga kerucut.

Note - Kerucut C cembung jika dan hanya jika untuk $ x, y \ di C, x + y \ di C $.

Bukti

Karena C adalah kerucut, untuk $ x, y \ di C \ Rightarrow \ lambda x \ di C$ and $\ mu y \ di C \: \ forall \: \ lambda, \ mu \ geq 0 $

C cembung jika $ \ lambda x + \ left (1- \ lambda \ right) y \ in C \: \ forall \: \ lambda \ in \ left (0, 1 \ right) $

Karena C adalah kerucut, $ \ lambda x \ dalam C$ and $\ kiri (1- \ lambda \ kanan) y \ di C \ Leftrightarrow x, y \ di C $

Jadi C cembung jika $ x + y \ dalam C $

Secara umum, jika $ x_1, x_2 \ di C$, then, $\ lambda_1x_1 + \ lambda_2x_2 \ in C, \ forall \ lambda_1, \ lambda_2 \ geq 0 $

Contoh

• Kombinasi kerucut dari himpunan vektor tak terhingga di $ \ mathbb {R} ^ n $ adalah kerucut cembung.

• Set kosong apa pun adalah kerucut cembung.

• Fungsi linier apa pun adalah kerucut cembung.

• Karena bidang-hiper linear, ia juga merupakan kerucut cembung.

• Setengah ruang tertutup juga merupakan kerucut cembung.

Note - Perpotongan dua kerucut cembung adalah kerucut cembung tetapi penyatuannya mungkin atau mungkin bukan kerucut cembung.

Misalkan S adalah himpunan tidak kosong di $ \ mathbb {R} ^ n$ Then, the polar cone of S denoted by $S ^ *$ is given by $S ^ * = \ kiri \ {p \ in \ mathbb {R} ^ n, p ^ Tx \ leq 0 \: \ untuk semua x \ dalam S \ kanan \} $.

Ucapan

• Kerucut kutub selalu cembung meskipun S bukan cembung.

• Jika S kosong, $ S ^ * = \ mathbb {R} ^ n $.

• Polaritas dapat dilihat sebagai generalisasi ortogonalitas.

Misalkan $ C \ subseteq \ mathbb {R} ^ n$ then the orthogonal space of C, denoted by $C ^ \ perp = \ kiri \ {y \ in \ mathbb {R} ^ n: \ left \ langle x, y \ right \ rangle = 0 \ forall x \ in C \ right \} $.

Kata pengantar singkat

Mari $ S, S_1$ and $S_2$ be non empty sets in $\ mathbb {R} ^ n $ maka pernyataan berikut ini benar -

• $ S ^ * $ adalah kerucut cembung tertutup.

• $ S \ subseteq S ^ {**}$ where $S ^ {**}$ is a polar cone of $S ^ * $.

• $ S_1 \ subseteq S_2 \ Rightarrow S_ {2} ^ {*} \ subseteq S_ {1} ^ {*} $.

Bukti

Step 1 - $ S ^ * = \ kiri \ {p \ in \ mathbb {R} ^ n, p ^ Tx \ leq 0 \: \ forall \: x \ in S \ right \} $

• Misalkan $ x_1, x_2 \ in S ^ * \ Rightarrow x_ {1} ^ {T} x \ leq 0 $ and $x_ {2} ^ {T} x \ leq 0, \ untuk semua x \ dalam S $

  Untuk $ \ lambda \ di \ kiri (0, 1 \ kanan), \ kiri [\ lambda x_1 + \ kiri (1- \ lambda \ kanan) x_2 \ kanan] ^ Tx = \ kiri [\ kiri (\ lambda x_1 \ kanan ) ^ T + \ kiri \ {\ kiri (1- \ lambda \ kanan) x_ {2} \ kanan \} ^ {T} \ kanan] x, \ untuk semua x \ dalam S $

  $ = \ kiri [\ lambda x_ {1} ^ {T} + \ kiri (1- \ lambda \ kanan) x_ {2} ^ {T} \ kanan] x = \ lambda x_ {1} ^ {T} x + \ kiri (1- \ lambda \ kanan) x_ {2} ^ {T} \ leq 0 $

  Jadi $ \ lambda x_1 + \ left (1- \ lambda \ right) x_ {2} \ in S ^ * $

  Oleh karena itu $ S ^ * $ adalah himpunan cembung.

• Untuk $ \ lambda \ geq 0, p ^ {T} x \ leq 0, \ forall \: x \ in S $

  Oleh karena itu, $ \ lambda p ^ T x \ leq 0, $

  $ \ Kananarrow \ kiri (\ lambda p \ kanan) ^ T x \ leq 0 $

  $ \ Rightarrow \ lambda p \ dalam S ^ * $

  Jadi, $ S ^ * $ adalah kerucut.

• Untuk menunjukkan $ S ^ *$ is closed, i.e., to show if $p_n \ rightarrow p$ as $n \ rightarrow \ infty$, then $p \ dalam S ^ * $

  $ \ untuk semua x \ dalam S, p_ {n} ^ {T} xp ^ T x = \ kiri (p_n-p \ kanan) ^ T x $

  Sebagai $ p_n \ rightarrow p$ as $n \ rightarrow \ infty \ Rightarrow \ left (p_n \ rightarrow p \ right) \ rightarrow 0 $

  Oleh karena itu $ p_ {n} ^ {T} x \ rightarrow p ^ {T} x$. But $p_ {n} ^ {T} x \ leq 0, \: \ untuk semua x \ dalam S $

  Jadi, $ p ^ Tx \ leq 0, \ forall x \ in S $

  $ \ Rightarrow p \ dalam S ^ * $

  Karenanya, $ S ^ * $ ditutup.

Step 2 - $ S ^ {**} = \ kiri \ {q \ in \ mathbb {R} ^ n: q ^ T p \ leq 0, \ untuk semua p \ dalam S ^ * \ kanan \} $

Misalkan $ x \ dalam S$, then $ \ Forall p \ in S ^ *, p ^ T x \ leq 0 \ Rightarrow x ^ Tp \ leq 0 \ Rightarrow x \ in S ^ {**} $

Jadi, $ S \ subseteq S ^ {**} $

Step 3 - $ S_2 ^ * = \ kiri \ {p \ in \ mathbb {R} ^ n: p ^ Tx \ leq 0, \ forall x \ in S_2 \ right \} $

Sejak $ S_1 \ subseteq S_2 \ Rightarrow \ forall x \ in S_2 \ Rightarrow \ forall x \ in S_1 $

Oleh karena itu, jika $ \ hat {p} \ dalam S_2 ^ *, $then $\ hat {p} ^ Tx \ leq 0, \ forall x \ in S_2 $

$ \ Rightarrow \ hat {p} ^ Tx \ leq 0, \ forall x \ in S_1 $

$ \ Rightarrow \ hat {p} ^ T \ in S_1 ^ * $

$ \ Rightarrow S_2 ^ * \ subseteq S_1 ^ * $

Dalil

Misal C adalah kerucut cembung tertutup yang tidak kosong, lalu $ C = C ^ ** $

Bukti

$ C = C ^ {**} $ oleh lemma sebelumnya.

Untuk membuktikan: $ x \ in C ^ {**} \ subseteq C $

Misalkan $ x \ dalam C ^ {**}$ and let $x \ notin C $

Kemudian dengan teorema pemisahan fundamental, terdapat sebuah vektor $ p \ neq 0$ and a scalar $\alfa$ such that $p ^ Ty \ leq \ alpha, \ forall y \ in C $

Oleh karena itu, $ p ^ Tx> \ alpha $

Tapi karena $ \ left (y = 0 \ right) \ di C$ and $p ^ Ty \ leq \ alpha, \ forall y \ in C \ Rightarrow \ alpha \ geq 0$ and $p ^ Tx> 0 $

Jika $ p \ notin C ^ *$, then there exists some $\ bar {y} \ di C$ such that $p ^ T \ bar {y}> 0$ and $p ^ T \ kiri (\ lambda \ bar {y} \ kanan)$ can be made arbitrarily large by taking $\ lambda $ cukup besar.

Ini bertentangan dengan fakta bahwa $ p ^ Ty \ leq \ alpha, \ forall y \ in C $

Oleh karena itu, $ p \ dalam C ^ * $

Karena $ x \ di C ^ * = \ left \ {q: q ^ Tp \ leq 0, \ forall p \ in C ^ * \ right \} $

Oleh karena itu, $ x ^ Tp \ leq 0 \ Rightarrow p ^ Tx \ leq 0 $

Tapi $ p ^ Tx> \ alpha $

Demikianlah kontradiksi.

Jadi, $ x \ dalam C $

Karenanya $ C = C ^ {**} $.

Titik dalam bentuk $ \ alpha_1x_1 + \ alpha_2x_2 + .... + \ alpha_nx_n$ with $\ alpha_1, \ alpha_2, ..., \ alpha_n \ geq 0$ is called conic combination of $x_1, x_2, ..., x_n. $

• Jika $ x_i$ are in convex cone C, then every conic combination of $x_i $ juga dalam C.

• Himpunan C adalah kerucut cembung jika mengandung semua kombinasi kerucut dari elemen-elemennya.

Conic Hull

Sebuah lambung berbentuk kerucut didefinisikan sebagai himpunan dari semua kombinasi kerucut dari himpunan S tertentu dan dilambangkan dengan coni (S).

Jadi, $ coni \ left (S \ right) = \ left \ {\ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda_ix_i: x_i \ in S, \ lambda_i \ in \ mathbb {R}, \ lambda_i \ geq 0, i = 1,2, ... \ kanan \} $

• Lambung berbentuk kerucut adalah satu set cembung.
• Asal selalu milik conic hull.

Himpunan dalam $ \ mathbb {R} ^ n $ dikatakan polihedral jika merupakan perpotongan dari sejumlah terbatas setengah spasi, yaitu,

$ S = \ kiri \ {x \ in \ mathbb {R} ^ n: p_ {i} ^ {T} x \ leq \ alpha_i, i = 1,2, ...., n \ kanan \} $

Sebagai contoh,

• $ \ kiri \ {x \ dalam \ mathbb {R} ^ n: AX = b \ right \} $

• $ \ kiri \ {x \ dalam \ mathbb {R} ^ n: AX \ leq b \ right \} $

• $ \ kiri \ {x \ dalam \ mathbb {R} ^ n: AX \ geq b \ right \} $

Kerucut Polyhedral

Satu set di $ \ mathbb {R} ^ n$ is said to be polyhedral cone if it is the intersection of a finite number of half spaces that contain the origin, i.e., $S = \ kiri \ {x \ dalam \ mathbb {R} ^ n: p_ {i} ^ {T} x \ leq 0, i = 1, 2, ... \ kanan \} $

Politop

Polytope adalah himpunan polihedral yang dibatasi.

Catatan

• Sebuah polytope adalah lambung cembung dari sekumpulan titik yang terbatas.
• Kerucut polihedral dihasilkan oleh sekumpulan vektor berhingga.
• Seperangkat polihedral adalah himpunan tertutup.
• Himpunan polihedral adalah himpunan cembung.

Misalkan S himpunan cembung di $ \ mathbb {R} ^ n$. A vector $x \ dalam S$ is said to be a extreme point of S if $x = \ lambda x_1 + \ kiri (1- \ lambda \ kanan) x_2$ with $x_1, x_2 \ dalam S$ and $\ lambda \ in \ left (0, 1 \ right) \ Rightarrow x = x_1 = x_2 $.

Contoh

Step 1 - $ S = \ kiri \ {\ kiri (x_1, x_2 \ kanan) \ dalam \ mathbb {R} ^ 2: x_ {1} ^ {2} + x_ {2} ^ {2} \ leq 1 \ kanan \ } $

Titik ekstrem, $ E = \ kiri \ {\ kiri (x_1, x_2 \ kanan) \ in \ mathbb {R} ^ 2: x_ {1} ^ {2} + x_ {2} ^ {2} = 1 \ kanan \} $

Step 2 - $ S = \ kiri \ {\ kiri (x_1, x_2 \ kanan) \ in \ mathbb {R} ^ 2: x_1 + x_2 <2, -x_1 + 2x_2 \ leq 2, x_1, x_2 \ geq 0 \ right \ } $

Titik ekstrim, $ E = \ kiri \ {\ kiri (0, 0 \ kanan), \ kiri (2, 0 \ kanan), \ kiri (0, 1 \ kanan), \ kiri (\ frac {2} {3 }, \ frac {4} {3} \ kanan) \ kanan \} $

Step 3 - S adalah polytope yang dibuat oleh titik $ \ kiri \ {\ kiri (0,0 \ kanan), \ kiri (1,1 \ kanan), \ kiri (1,3 \ kanan), \ kiri (-2, 4 \ kanan), \ kiri (0,2 \ kanan) \ kanan \} $

Titik ekstrim, $ E = \ kiri \ {\ kiri (0,0 \ kanan), \ kiri (1,1 \ kanan), \ kiri (1,3 \ kanan), \ kiri (-2,4 \ kanan) \ kanan \} $

Catatan

• Titik mana pun dari himpunan cembung S, dapat direpresentasikan sebagai kombinasi cembung dari titik ekstremnya.

• Ini hanya benar untuk set tertutup dan berbatas di $ \ mathbb {R} ^ n $.

• Ini mungkin tidak benar untuk set tak terbatas.

k poin ekstrim

Sebuah titik dalam himpunan cembung disebut k ekstrim jika dan hanya jika titik interior himpunan cembung berdimensi-k di dalam S, dan bukan titik interior himpunan cembung berdimensi a (k + 1) di dalam S. Pada dasarnya, untuk himpunan cembung S, titik ekstrem k membuat sisi terbuka berdimensi-k.

Misalkan S adalah himpunan konveks tertutup di $ \ mathbb {R} ^ n$. A non zero vector $d \ in \ mathbb {R} ^ n$ is called a direction of S if for each $x \ di S, x + \ lambda d \ di S, \ forall \ lambda \ geq 0. $

• Dua arah $ d_1$ and $d_2$ of S are called distinct if $d \ neq \ alpha d_2$ for $ \ alpha> 0 $.

• Arah $ d$ of $S$ is said to be extreme direction if it cannot be written as a positive linear combination of two distinct directions, i.e., if $d = \ lambda _1d_1 + \ lambda _2d_2$ for $\ lambda _1, \ lambda _2> 0$, then $d_1 = \ alpha d_2$ for some $\ alpha $.

• Arah lain apa pun dapat dinyatakan sebagai kombinasi positif dari arah ekstrem.

• Untuk set cembung $ S$, the direction d such that $x + \ lambda d \ dalam S$ for some $x \ dalam S$ and all $\ lambda \ geq0 $ dipanggil recessive seharga $ S $.

• Misalkan E himpunan titik-titik di mana fungsi tertentu $ f: S \ rightarrow$ over a non-empty convex set S in $\ mathbb {R} ^ n$ attains its maximum, then $E$ is called exposed face of $S $. Arah dari wajah yang terbuka disebut arah yang terbuka.

• Sinar yang arahnya ekstrim disebut sinar ekstrim.

Contoh

Perhatikan fungsi $ f \ left (x \ right) = y = \ left | x \ right |$, where $x \ in \ mathbb {R} ^ n$. Let d be unit vector in $\ mathbb {R} ^ n $

Kemudian, d adalah arah untuk fungsi f karena untuk $ \ lambda \ geq 0, x + \ lambda d \ in f \ left (x \ right) $.

Misalkan $ f: S \ rightarrow \ mathbb {R}$, where S is non empty convex set in $\ mathbb {R} ^ n$, then $f \ kiri (x \ kanan)$ is said to be convex on S if $f \ kiri (\ lambda x_1 + \ kiri (1- \ lambda \ kanan) x_2 \ kanan) \ leq \ lambda f \ kiri (x_1 \ kanan) + \ kiri (1- \ lambda \ kanan) f \ kiri (x_2 \ kanan), \ depan \ lambda \ dalam \ kiri (0,1 \ kanan) $.

Di sisi lain, Misalkan $ f: S \ rightarrow \ mathbb {R}$, where S is non empty convex set in $\ mathbb {R} ^ n$, then $f \ kiri (x \ kanan)$ is said to be concave on S if $f \ kiri (\ lambda x_1 + \ kiri (1- \ lambda \ kanan) x_2 \ kanan) \ geq \ lambda f \ kiri (x_1 \ kanan) + \ kiri (1- \ lambda \ kanan) f \ kiri (x_2 \ kanan), \ depan \ lambda \ di \ kiri (0, 1 \ kanan) $.

Misalkan $ f: S \ rightarrow \ mathbb {R}$ where S is non empty convex set in $\ mathbb {R} ^ n$, then $f \ kiri (x \ kanan)$ is said to be strictly convex on S if $f \ kiri (\ lambda x_1 + \ kiri (1- \ lambda \ kanan) x_2 \ kanan) <\ lambda f \ kiri (x_1 \ kanan) + \ kiri (1- \ lambda \ kanan) f \ kiri (x_2 \ kanan ), \ depan \ lambda \ di \ kiri (0, 1 \ kanan) $.

Misalkan $ f: S \ rightarrow \ mathbb {R}$ where S is non empty convex set in $\ mathbb {R} ^ n$, then $f \ kiri (x \ kanan)$ is said to be strictly concave on S if $f \ kiri (\ lambda x_1 + \ kiri (1- \ lambda \ kanan) x_2 \ kanan)> \ lambda f \ kiri (x_1 \ kanan) + \ kiri (1- \ lambda \ kanan) f \ kiri (x_2 \ kanan ), \ depan \ lambda \ di \ kiri (0, 1 \ kanan) $.

Contoh

• Fungsi linier adalah cembung dan cekung.

• $ f \ kiri (x \ kanan) = \ kiri | x \ kanan | $ adalah fungsi cembung.

• $ f \ left (x \ right) = \ frac {1} {x} $ adalah fungsi cembung.

Dalil

Misalkan $ f_1, f_2, ..., f_k: \ mathbb {R} ^ n \ rightarrow \ mathbb {R}$ be convex functions. Consider the function $f \ kiri (x \ kanan) = \ displaystyle \ sum \ batas_ {j = 1} ^ k \ alpha_jf_j \ kiri (x \ kanan)$ where $\ alpha_j> 0, j = 1, 2, ... k,$ then $f \ left (x \ right) $ adalah fungsi cembung.

Bukti

Karena $ f_1, f_2, ... f_k $ adalah fungsi konveks

Oleh karena itu, $ f_i \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda f_i \ left (x_1 \ right) + \ left (1- \ lambda \ right) f_i \ left (x_2 \ kanan), \ depan \ lambda \ di \ kiri (0, 1 \ kanan)$ and $i = 1, 2, ...., k $

Pertimbangkan fungsi $ f \ left (x \ right) $.

Karena itu,

$ f \ kiri (\ lambda x_1 + \ kiri (1- \ lambda \ kanan) x_2 \ kanan) $

$ = \ displaystyle \ sum \ limit_ {j = 1} ^ k \ alpha_jf_j \ left (\ lambda x_1 + 1- \ lambda \ right) x_2 \ leq \ displaystyle \ sum \ limit_ {j = 1} ^ k \ alpha_j \ lambda f_j \ kiri (x_1 \ kanan) + \ kiri (1- \ lambda \ kanan) f_j \ kiri (x_2 \ kanan) $

$ \ Panah kanan f \ kiri (\ lambda x_1 + \ kiri (1- \ lambda \ kanan) x_2 \ kanan) \ leq \ lambda \ kiri (\ displaystyle \ sum \ limit_ {j = 1} ^ k \ alpha _jf_j \ kiri ( x_1 \ kanan) \ kanan) + \ kiri (\ displaystyle \ sum \ batas_ {j = 1} ^ k \ alpha _jf_j \ kiri (x_2 \ kanan) \ kanan) $

$ \ Kanan kanan f \ kiri (\ lambda x_1 + \ kiri (1- \ lambda \ kanan) x_2 \ kanan) \ leq \ lambda f \ kiri (x_2 \ kanan) \ leq \ kiri (1- \ lambda \ kanan) f \ kiri (x_2 \ kanan) $

Karenanya, $ f \ left (x \ right) $ adalah fungsi cembung.

Dalil

Misalkan $ f \ kiri (x \ kanan)$ be a convex function on a convex set $S \ subset \ mathbb {R} ^ n$ then a local minima of $f \ left (x \ right) $ pada S adalah minimum global.

Bukti

Mari $ \ hat {x}$ be a local minima for $f \ kiri (x \ kanan)$ and $\ hat {x} $ bukanlah nilai minimum global.

oleh karena itu, $ \ existing \ hat {x} \ di S$ such that $f \ kiri (\ bar {x} \ kanan) <f \ kiri (\ hat {x} \ kanan) $

Sejak $ \ hat {x}$ is a local minima, there exists neighbourhood $N_ \ varepsilon \ kiri (\ hat {x} \ kanan)$ such that $f \ kiri (\ hat {x} \ kanan) \ leq f \ kiri (x \ kanan), \ depan x \ di N_ \ varepsilon \ kiri (\ hat {x} \ kanan) \ cap S $

Tapi $ f \ kiri (x \ kanan)$ is a convex function on S, therefore for $\ lambda \ in \ left (0, 1 \ kanan) $

kita memiliki $ \ lambda \ hat {x} + \ left (1- \ lambda \ right) \ bar {x} \ leq \ lambda f \ left (\ hat {x} \ right) + \ left (1- \ lambda \ kanan) f \ kiri (\ bar {x} \ kanan) $

$ \ Rightarrow \ lambda \ hat {x} + \ left (1- \ lambda \ right) \ bar {x} <\ lambda f \ left (\ hat {x} \ kanan) + \ kiri (1- \ lambda \ kanan) f \ kiri (\ hat {x} \ kanan) $

$ \ Rightarrow \ lambda \ hat {x} + \ left (1- \ lambda \ right) \ bar {x} <f \ left (\ hat {x} \ kanan), \ depan \ lambda \ in \ kiri (0 , 1 \ kanan) $

Tetapi untuk beberapa $ \ lambda <1 $ tetapi mendekati 1, kami punya

$ \ lambda \ hat {x} + \ kiri (1- \ lambda \ kanan) \ bar {x} \ di N_ \ varepsilon \ kiri (\ hat {x} \ kanan) \ cap S$ and $f \ kiri (\ lambda \ hat {x} + \ kiri (1- \ lambda \ kanan) \ bar {x} \ kanan) <f \ kiri (\ bar {x} \ kanan) $

yang merupakan kontradiksi.

Karenanya, $ \ bar {x} $ adalah nilai minimum global.

Prasasti

biarkan S menjadi himpunan bagian yang tidak kosong di $ \ mathbb {R} ^ n$ and let $f: S \ rightarrow \ mathbb {R}$ then the epigraph of f denoted by epi(f) or $E_f$ is a subset of $\ mathbb {R} ^ n + 1$ defined by $E_f = \ left \ {\ left (x, \ alpha \ right): x \ in \ mathbb {R} ^ n, \ alpha \ in \ mathbb {R}, f \ left (x \ right) \ leq \ alpha \ kanan \} $

Hipograf

biarkan S menjadi himpunan bagian yang tidak kosong di $ \ mathbb {R} ^ n$ and let $f: S \ rightarrow \ mathbb {R}$, then the hypograph of f denoted by hyp(f) or $H_f = \ left \ {\ left (x, \ alpha \ right): x \ in \ mathbb {R} ^ n, \ alpha \ in \ mathbb {R} ^ n, \ alpha \ in \ mathbb {R}, f \ kiri (x \ kanan) \ geq \ alpha \ kanan \} $

Dalil

Misalkan S adalah cembung tidak kosong yang ditetapkan di $ \ mathbb {R} ^ n$ and let $f: S \ rightarrow \ mathbb {R} ^ n$, then f is convex if and only if its epigraph $E_f $ adalah himpunan cembung.

Bukti

Misalkan f adalah fungsi cembung.

Untuk menampilkan $ E_f $ adalah himpunan cembung.

Misalkan $ \ left (x_1, \ alpha_1 \ right), \ left (x_2, \ alpha_2 \ right) \ in E_f, \ lambda \ in \ left (0, 1 \ right) $

Untuk menampilkan $ \ lambda \ kiri (x_1, \ alpha_1 \ kanan) + \ kiri (1- \ lambda \ kanan) \ kiri (x_2, \ alpha_2 \ kanan) \ dalam E_f $

$ \ Kananarrow \ kiri [\ lambda x_1 + \ kiri (1- \ lambda \ kanan) x_2, \ lambda \ alpha_1 + \ kiri (1- \ lambda \ kanan) \ alpha_2 \ kanan] \ di E_f $

$ f \ kiri (x_1 \ kanan) \ leq \ alpha _1, f \ kiri (x_2 \ kanan) \ leq \ alpha _2 $

Oleh karena itu, $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2 \ kanan) $

$ \ Kanan kanan f \ kiri (\ lambda x_1 + \ kiri (1- \ lambda \ kanan) x_2 \ kanan) \ leq \ lambda \ alpha_1 + \ kiri (1- \ lambda \ kanan) \ alpha_2 $

Berbicara

Misalkan $ E_f $ adalah himpunan konveks.

Untuk menunjukkan f adalah cembung.

yaitu, untuk menunjukkan jika $ x_1, x_2 \ in S, \ lambda \ left (0, 1 \ right) $

$ f \ kiri (\ lambda x_1 + \ kiri (1- \ lambda \ kanan) x_2 \ kanan) \ leq \ lambda f \ kiri (x_1 \ kanan) + \ kiri (1- \ lambda \ kanan) f \ kiri (x_2 \ benar) $

Misalkan $ x_1, x_2 \ in S, \ lambda \ in \ left (0, 1 \ right), f \ left (x_1 \ right), f \ left (x_2 \ right) \ in \ mathbb {R} $

Sejak $ E_f$ is a convex set, $\ kiri (\ lambda x_1 + \ kiri (1- \ lambda \ kanan) x_2, \ lambda f \ kiri (x_1 \ kanan) + \ kiri (1- \ lambda \ kanan) \ kanan) f \ kiri (x_2 \ kanan) \ dalam E_f $

Oleh karena itu, $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2 \ kanan) $

Misalkan S adalah cembung tidak kosong yang ditetapkan di $ \ mathbb {R} ^ n$ and $f: S \ rightarrow \ mathbb {R} ^ n$. Then f is convex if and only if for each integer $k> 0 $

$ x_1, x_2, ... x_k \ in S, \ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda_i = 1, \ lambda_i \ geq 0, \ forall i = 1,2, s, k$, we have $f \ kiri (\ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda_ix_i \ kanan) \ leq \ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda _if \ kiri (x \ kanan) $

Bukti

Dengan induksi pada k.

$ k = 1: x_1 \ dalam S$ Therefore $f \ kiri (\ lambda_1 x_1 \ kanan) \ leq \ lambda_i f \ kiri (x_1 \ kanan)$ because $\ lambda_i = 1 $.

$ k = 2: \ lambda_1 + \ lambda_2 = 1$ and $x_1, x_2 \ dalam S $

Karenanya, $ \ lambda_1x_1 + \ lambda_2x_2 \ dalam S $

Karenanya, menurut definisi, $ f \ left (\ lambda_1 x_1 + \ lambda_2 x_2 \ right) \ leq \ lambda _1f \ left (x_1 \ right) + \ lambda _2f \ left (x_2 \ right) $

Biarkan pernyataan itu benar untuk $ n <k $

Karena itu,

$ f \ kiri (\ lambda_1 x_1 + \ lambda_2 x_2 + .... + \ lambda_k x_k \ kanan) \ leq \ lambda_1 f \ kiri (x_1 \ kanan) + \ lambda_2 f \ kiri (x_2 \ kanan) + ... + \ lambda_k f \ kiri (x_k \ kanan) $

$ k = n + 1:$ Let $x_1, x_2, .... x_n, x_ {n + 1} \ dalam S$ and $\ displaystyle \ sum \ limit_ {i = 1} ^ {n + 1} = 1 $

Oleh karena itu $ \ mu_1x_1 + \ mu_2x_2 + ....... + \ mu_nx_n + \ mu_ {n + 1} x_ {n + 1} \ in S $

jadi, $ f \ kiri (\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n + \ mu_ {n + 1} x_ {n + 1} \ kanan) $

$ = f \ kiri (\ kiri (\ mu_1 + \ mu_2 + ... + \ mu_n \ kanan) \ frac {\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n} {\ mu_1 + \ mu_2 + \ mu_3} + \ mu_ {n + 1} x_ {n + 1} \ kanan) $

$ = f \ kiri (\ mu_y + \ mu_ {n + 1} x_ {n + 1} \ kanan)$ where $\ mu = \ mu_1 + \ mu_2 + ... + \ mu_n $ dan

$ y = \ frac {\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n} {\ mu_1 + \ mu_2 + ... + \ mu_n}$ and also $\ mu_1 + \ mu_ {n + 1} = 1, y \ dalam S $

$ \ Sisi kanan f \ kiri (\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n + \ mu_ {n + 1} x_ {n + 1} \ kanan) \ leq \ mu f \ kiri (y \ kanan) + \ mu_ {n +1} f \ kiri (x_ {n + 1} \ kanan) $

$ \ Sisi kanan f \ kiri (\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n + \ mu_ {n + 1} x_ {n + 1} \ kanan) \ leq $

$ \ kiri (\ mu_1 + \ mu_2 + ... + \ mu_n \ kanan) f \ kiri (\ frac {\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n} {\ mu_1 + \ mu_2 + ... + \ mu_n} \ kanan) + \ mu_ {n + 1} f \ kiri (x_ {n + 1} \ kanan) $

$ \ Sisi kanan f \ kiri (\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n + \ mu_ {n + 1} x_ {n + 1} \ kanan) \ leq \ kiri (\ mu_1 + \ mu_2 + ... + \ mu_n \ benar) $

$ \ kiri [\ frac {\ mu_1} {\ mu_1 + \ mu_2 + ... + \ mu_n} f \ kiri (x_1 \ kanan) + ... + \ frac {\ mu_n} {\ mu_1 + \ mu_2 + ... + \ mu_n} f \ kiri (x_n \ kanan) \ kanan] + \ mu_ {n + 1} f \ kiri (x_ {n + 1} \ kanan) $

$ \ Sisi kanan f \ kiri (\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n + \ mu_ {n + 1} x_ {n + 1} \ kanan) \ leq \ mu_1f \ kiri (x_1 \ kanan) + \ mu_2f \ kiri ( x_2 \ kanan) + .... $

Oleh karena itu Terbukti.

Misalkan S adalah himpunan terbuka tidak kosong di $ \ mathbb {R} ^ n$,then $f: S \ rightarrow \ mathbb {R}$ is said to be differentiable at $\ hat {x} \ in S$ if there exist a vector $\ bigtriangledown f \ left (\ hat {x} \ kanan)$ called gradient vector and a function $\ alpha: \ mathbb {R} ^ n \ rightarrow \ mathbb {R} $ seperti itu

$ f \ kiri (x \ kanan) = f \ kiri (\ topi {x} \ kanan) + \ bigtriangledown f \ kiri (\ topi {x} \ kanan) ^ T \ kiri (x- \ topi {x} \ kanan) + \ kiri \ | x = \ hat {x} \ right \ | \ alpha \ left (\ hat {x}, x- \ hat {x} \ right), \ forall x \ in S $ di mana

$ \ alpha \ left (\ hat {x}, x- \ hat {x} \ right) \ rightarrow 0 \ bigtriangledown f \ left (\ hat {x} \ right) = \ left [\ frac {\ partial f} {\ sebagian x_1} \ frac {\ sebagian f} {\ sebagian x_2} ... \ frac {\ sebagian f} {\ sebagian x_n} \ kanan] _ {x = \ hat {x}} ^ {T} $

Dalil

biarkan S menjadi himpunan konveks terbuka yang tidak kosong di $ \ mathbb {R} ^ n$ and let $f: S \ rightarrow \ mathbb {R}$ be differentiable on S. Then, f is convex if and only if for $x_1, x_2 \ di S, \ bigtriangledown f \ kiri (x_2 \ kanan) ^ T \ kiri (x_1-x_2 \ kanan) \ leq f \ kiri (x_1 \ kanan) -f \ kiri (x_2 \ kanan) $

Bukti

Misalkan f adalah fungsi cembung. yaitu, untuk $ x_1, x_2 \ in S, \ lambda \ in \ left (0, 1 \ right) $

$ f \ kiri [\ lambda x_1 + \ kiri (1- \ lambda \ kanan) x_2 \ kanan] \ leq \ lambda f \ kiri (x_1 \ kanan) + \ kiri (1- \ lambda \ kanan) f \ kiri (x_2 \ benar) $

$ \ Kanan ke kanan f \ kiri [\ lambda x_1 + \ kiri (1- \ lambda \ kanan) x_2 \ kanan] \ leq \ lambda \ kiri (f \ kiri (x_1 \ kanan) -f \ kiri (x_2 \ kanan) \ kanan ) + f \ kiri (x_2 \ kanan) $

$ \ Kananarrow \ lambda \ kiri (f \ kiri (x_1 \ kanan) -f \ kiri (x_2 \ kanan) \ kanan) \ geq f \ kiri (x_2 + \ lambda \ kiri (x_1-x_2 \ kanan) \ kanan) - f \ kiri (x_2 \ kanan) $

$ \ Kananarrow \ lambda \ kiri (f \ kiri (x_1 \ kanan) -f \ kiri (x_2 \ kanan) \ kanan) \ geq f \ kiri (x_2 \ kanan) + \ bigtriangledown f \ kiri (x_2 \ kanan) ^ T \ kiri (x_1-x_2 \ kanan) \ lambda + $

$ \ kiri \ | \ lambda \ kiri (x_1-x_2 \ kanan) \ kanan \ | \ alpha \ kiri (x_2, \ lambda \ kiri (x_1 - x_2 \ kanan) -f \ kiri (x_2 \ kanan) \ kanan) $

di mana $ \ alpha \ left (x_2, \ lambda \ left (x_1 - x_2 \ right) \ right) \ rightarrow 0$ as$\ lambda \ rightarrow 0 $

Membagi dengan $ \ lambda $ di kedua sisi, kita dapatkan -

$ f \ kiri (x_1 \ kanan) -f \ kiri (x_2 \ kanan) \ geq \ bigtriangledown f \ kiri (x_2 \ kanan) ^ T \ kiri (x_1-x_2 \ kanan) $

Berbicara

Misalkan untuk $ x_1, x_2 \ in S, \ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_1-x_2 \ right) \ leq f \ left (x_1 \ right) -f \ left (x_2 \ right) $

Untuk menunjukkan bahwa f cembung.

Karena S cembung, $ x_3 = \ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ in S, \ lambda \ in \ left (0, 1 \ right) $

Karena itu, sejak $ x_1, x_3 \ dalam S $

$ f \ kiri (x_1 \ kanan) -f \ kiri (x_3 \ kanan) \ geq \ bigtriangledown f \ kiri (x_3 \ kanan) ^ T \ kiri (x_1 -x_3 \ kanan) $

$ \ Panah kanan f \ kiri (x_1 \ kanan) -f \ kiri (x_3 \ kanan) \ geq \ bigtriangledown f \ kiri (x_3 \ kanan) ^ T \ kiri (x_1 - \ lambda x_1- \ kiri (1- \ lambda \ kanan) x_2 \ kanan) $

$ \ Rightarrow f \ left (x_1 \ right) -f \ left (x_3 \ right) \ geq \ left (1- \ lambda \ right) \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_1 - x_2 \ benar) $

Karena, $ x_2, x_3 \ dalam S $ karenanya

$ f \ kiri (x_2 \ kanan) -f \ kiri (x_3 \ kanan) \ geq \ bigtriangledown f \ kiri (x_3 \ kanan) ^ T \ kiri (x_2-x_3 \ kanan) $

$ \ Rightarrow f \ left (x_2 \ right) -f \ left (x_3 \ right) \ geq \ bigtriangledown f \ left (x_3 \ right) ^ T \ kiri (x_2- \ lambda x_1- \ kiri (1- \ lambda \ kanan) x_2 \ kanan) $

$ \ Rightarrow f \ left (x_2 \ right) -f \ left (x_3 \ right) \ geq \ left (- \ lambda \ right) \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_1-x_2 \ benar) $

Jadi, dengan menggabungkan persamaan di atas, kita mendapatkan -

$ \ lambda \ kiri (f \ kiri (x_1 \ kanan) -f \ kiri (x_3 \ kanan) \ kanan) + \ kiri (1- \ lambda \ kanan) \ kiri (f \ kiri (x_2 \ kanan) -f \ kiri (x_3 \ kanan) \ kanan) \ geq 0 $

$ \ Panah kanan f \ kiri (x_3 \ kanan) \ leq \ lambda f \ kiri (x_1 \ kanan) + \ kiri (1- \ lambda \ kanan) f \ kiri (x_2 \ kanan) $

Dalil

misalkan S adalah cembung terbuka tidak kosong yang disetel dalam $ \ mathbb {R} ^ n$ and let $f: S \ rightarrow \ mathbb {R}$ be differentiable on S, then f is convex on S if and only if for any $x_1, x_2 \ in S, \ left (\ bigtriangledown f \ left (x_2 \ right) - \ bigtriangledown f \ left (x_1 \ kanan) \ kanan) ^ T \ kiri (x_2-x_1 \ kanan) \ geq 0 $

Bukti

biarkan f menjadi fungsi cembung, lalu gunakan teorema sebelumnya -

$ \ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_1-x_2 \ kanan) \ leq f \ kiri (x_1 \ kanan) -f \ kiri (x_2 \ kanan) $ dan

$ \ bigtriangledown f \ kiri (x_1 \ kanan) ^ T \ kiri (x_2-x_1 \ kanan) \ leq f \ kiri (x_2 \ kanan) -f \ kiri (x_1 \ kanan) $

Menambahkan dua persamaan di atas, kita mendapatkan -

$ \ bigtriangledown f \ kiri (x_2 \ kanan) ^ T \ kiri (x_1-x_2 \ kanan) + \ bigtriangledown f \ kiri (x_1 \ kanan) ^ T \ kiri (x_2-x_1 \ kanan) \ leq 0 $

$ \ Rightarrow \ left (\ bigtriangledown f \ left (x_2 \ right) - \ bigtriangledown f \ left (x_1 \ kanan) \ kanan) ^ T \ kiri (x_1-x_2 \ kanan) \ leq 0 $

$ \ Rightarrow \ left (\ bigtriangledown f \ left (x_2 \ right) - \ bigtriangledown f \ left (x_1 \ kanan) \ kanan) ^ T \ kiri (x_2-x_1 \ kanan) \ geq 0 $

Berbicara

Biarkan untuk $ x_1, x_2 \ in S, \ left (\ bigtriangledown f \ left (x_2 \ right) - \ bigtriangledown f \ left (x_1 \ right) \ right) ^ T \ left (x_2-x_1 \ right) \ geq 0 $

Untuk menunjukkan bahwa f cembung.

Misalkan $ x_1, x_2 \ dalam S$, thus by mean value theorem, $\ frac {f \ left (x_1 \ right) -f \ left (x_2 \ right)} {x_1-x_2} = \ bigtriangledown f \ left (x \ right), x \ in \ left (x_1-x_2 \ right) \ Rightarrow x = \ lambda x_1 + \ left (1- \ lambda \ right) x_2 $ karena S adalah himpunan cembung.

$ \ Rightarrow f \ left (x_1 \ right) - f \ left (x_2 \ right) = \ left (\ bigtriangledown f \ left (x \ right) ^ T \ right) \ kiri (x_1-x_2 \ kanan) $

untuk $ x, x_1 $, kami tahu -

$ \ kiri (\ bigtriangledown f \ kiri (x \ kanan) - \ bigtriangledown f \ kiri (x_1 \ kanan) \ kanan) ^ T \ kiri (x-x_1 \ kanan) \ geq 0 $

$ \ Rightarrow \ left (\ bigtriangledown f \ left (x \ right) - \ bigtriangledown f \ left (x_1 \ right) \ kanan) ^ T \ kiri (\ lambda x_1 + \ kiri (1- \ lambda \ kanan) x_2- x_1 \ kanan) \ geq 0 $

$ \ Rightarrow \ left (\ bigtriangledown f \ left (x \ right) - \ bigtriangledown f \ left (x_1 \ right) \ kanan) ^ T \ kiri (1- \ lambda \ kanan) \ kiri (x_2-x_1 \ kanan ) \ geq 0 $

$ \ Rightarrow \ bigtriangledown f \ left (x \ right) ^ T \ left (x_2-x_1 \ right) \ geq \ bigtriangledown f \ left (x_1 \ right) ^ T \ kiri (x_2-x_1 \ kanan) $

Menggabungkan persamaan di atas, kita mendapatkan -

$ \ Kananarrow \ bigtriangledown f \ kiri (x_1 \ kanan) ^ T \ kiri (x_2-x_1 \ kanan) \ leq f \ kiri (x_2 \ kanan) -f \ kiri (x_1 \ kanan) $

Karenanya, menggunakan teorema terakhir, f adalah fungsi cembung.

Fungsi yang Dapat Dibedakan Dua Kali

Misalkan S adalah subset yang tidak kosong dari $ \ mathbb {R} ^ n$ and let $f: S \ rightarrow \ mathbb {R}$ then f is said to be twice differentiable at $\ bar {x} \ dalam S$ if there exists a vector $\ bigtriangledown f \ left (\ bar {x} \ kanan), a \: nXn$ matrix $H \ kiri (x \ kanan)$(called Hessian matrix) and a function $\ alpha: \ mathbb {R} ^ n \ rightarrow \ mathbb {R}$ such that $f \ kiri (x \ kanan) = f \ kiri (\ bar {x} + x- \ bar {x} \ kanan) = f \ kiri (\ bar {x} \ kanan) + \ bigtriangledown f \ kiri (\ bilah {x} \ kanan) ^ T \ kiri (x- \ bar {x} \ kanan) + \ frac {1} {2} \ kiri (x- \ bar {x} \ kanan) H \ kiri (\ bar {x} \ kanan) \ kiri (x- \ bar {x} \ kanan) $

di mana $ \ alpha \ left (\ bar {x}, x- \ bar {x} \ right) \ rightarrow Oasx \ rightarrow \ bar {x} $

Dalil

Misalkan f dua kali fungsi terdiferensiasi. Jika $ \ bar {x}$ is a local minima, then $\ bigtriangledown f \ left (\ bar {x} \ right) = 0$ and the Hessian matrix $H \ left (\ bar {x} \ right) $ adalah positif semidefinite.

Bukti

Misalkan $ d \ in \ mathbb {R} ^ n$. Since f is twice differentiable at $\ bar {x} $.

Karena itu,

$ f \ kiri (\ bar {x} + \ lambda d \ kanan) = f \ kiri (\ bar {x} \ kanan) + \ lambda \ bigtriangledown f \ kiri (\ bar {x} \ kanan) ^ T d + \ lambda ^ 2d ^ TH \ kiri (\ bar {x} \ kanan) d + \ lambda ^ 2d ^ TH \ kiri (\ bar {x} \ kanan) d + $

$ \ lambda ^ 2 \ kiri \ | d \ kanan \ | ^ 2 \ beta \ kiri (\ bar {x}, \ lambda d \ kanan) $

Tapi $ \ bigtriangledown f \ left (\ bar {x} \ right) = 0$ and $\ beta \ left (\ bar {x}, \ lambda d \ right) \ rightarrow 0$ as $\ lambda \ rightarrow 0 $

$ \ Rightarrow f \ left (\ bar {x} + \ lambda d \ right) -f \ left (\ bar {x} \ right) = \ lambda ^ 2d ^ TH \ kiri (\ bar {x} \ kanan) d $

Sejak $ \ bar {x}$ is a local minima, there exists a $\ delta> 0$ such that $f \ kiri (x \ kanan) \ leq f \ kiri (\ bar {x} + \ lambda d \ kanan), \ depan \ lambda \ in \ kiri (0, \ delta \ kanan) $

Dalil

Misalkan $ f: S \ rightarrow \ mathbb {R} ^ n$ where $S \ subset \ mathbb {R} ^ n$ be twice differentiable over S. If $\ bigtriangledown f \ left (x \ right) = 0$ and $H \ kiri (\ bar {x} \ kanan)$ is positive semi-definite, for all $x \ dalam S$, then $\ bar {x} $ adalah solusi optimal global.

Bukti

Sejak $ H \ kiri (\ bar {x} \ kanan)$ is positive semi-definite, f is convex function over S. Since f is differentiable and convex at $\ bar {x} $

$ \ bigtriangledown f \ kiri (\ bar {x} \ kanan) ^ T \ kiri (x- \ bar {x} \ kanan) \ leq f \ kiri (x \ kanan) -f \ kiri (\ bar {x} \ kanan), \ untuk semua x \ dalam S $

Karena $ \ bigtriangledown f \ left (\ bar {x} \ right) = 0, f \ left (x \ right) \ geq f \ left (\ bar {x} \ right) $

Karenanya, $ \ bar {x} $ adalah optima global.

Dalil

Misalkan $ \ bar {x} \ dalam S$ is a local optimal solution to the problem $f: S \ rightarrow \ mathbb {R}$ where S is a non-empty subset of $\ mathbb {R} ^ n$ and S is convex. $min \: f \ kiri (x \ kanan)$ where $x \ dalam S $.

Kemudian:

• $ \ bar {x} $ adalah solusi optimal global.

• Jika $ \ bar {x}$ is strictly local minima or f is strictly convex function, then $\ bar {x} $ adalah solusi optimal global yang unik dan juga minimum lokal yang kuat.

Bukti

Biarkan $ \ bar {x}$ be another global optimal solution to the problem such that $x \ neq \ bar {x}$ and $f \ kiri (\ bar {x} \ kanan) = f \ kiri (\ topi {x} \ kanan) $

Sejak $ \ hat {x}, \ bar {x} \ in S$ and S is convex, then $\ frac {\ hat {x} + \ bar {x}} {2} \ dalam S $ dan f benar-benar cembung.

$ \ Rightarrow f \ left (\ frac {\ hat {x} + \ bar {x}} {2} \ right) <\ frac {1} {2} f \ left (\ bar {x} \ kanan) + \ frac {1} {2} f \ left (\ hat {x} \ right) = f \ left (\ hat {x} \ kanan) $

Ini kontradiksi.

Karenanya, $ \ hat {x} $ adalah solusi optimal global yang unik.

Akibat wajar

Misalkan $ f: S \ subset \ mathbb {R} ^ n \ rightarrow \ mathbb {R}$ be a differentiable convex function where $\ phi \ neq S \ subset \ mathbb {R} ^ n$ is a convex set. Consider the problem $min f \ kiri (x \ kanan), x \ dalam S$,then $\ bar {x}$ is an optimal solution if $\ bigtriangledown f \ left (\ bar {x} \ right) ^ T \ left (x- \ bar {x} \ right) \ geq 0, \ forall x \ in S. $

Bukti

Biarkan $ \ bar {x}$ is an optimal solution, i.e, $f \ kiri (\ bar {x} \ kanan) \ leq f \ kiri (x \ kanan), \ depan x \ dalam S $

$ \ Panah kanan f \ kiri (x \ kanan) = f \ kiri (\ bar {x} \ kanan) \ geq 0 $

$ f \ kiri (x \ kanan) = f \ kiri (\ bar {x} \ kanan) + \ bigtriangledown f \ kiri (\ bar {x} \ kanan) ^ T \ kiri (x- \ bar {x} \ kanan) + \ kiri \ | x- \ bar {x} \ kanan \ | \ alpha \ kiri (\ bar {x}, x- \ bar {x} \ kanan) $

di mana $ \ alpha \ left (\ bar {x}, x- \ bar {x} \ right) \ rightarrow 0$ as $x \ rightarrow \ bar {x} $

$ \ Rightarrow f \ left (x \ right) -f \ left (\ bar {x} \ right) = \ bigtriangledown f \ left (\ bar {x} \ kanan) ^ T \ kiri (x- \ bar {x } \ kanan) \ geq 0 $

Akibat wajar

Misalkan f adalah fungsi cembung yang dapat dibedakan pada $ \ bar {x}$,then $\ bar {x}$ is global minimum iff $\ bigtriangledown f \ left (\ bar {x} \ right) = 0 $

Contoh

• $ f \ kiri (x \ kanan) = \ kiri (x ^ 2-1 \ kanan) ^ {3}, x \ dalam \ mathbb {R} $.

  $ \ Bigtriangledown f \ left (x \ right) = 0 \ Rightarrow x = -1,0,1 $.

  $ \ bigtriangledown ^ 2f \ left (\ pm 1 \ right) = 0, \ bigtriangledown ^ 2 f \ left (0 \ right) = 6> 0 $.

  $ f \ kiri (\ pm 1 \ kanan) = 0, f \ kiri (0 \ kanan) = - 1 $

  Oleh karena itu, $ f \ left (x \ right) \ geq -1 = f \ left (0 \ right) \ Rightarrow f \ left (0 \ right) \ leq f \ left (x \ right) \ forall x \ in \ mathbb {R} $

• $ f \ kiri (x \ kanan) = x \ log x$ defined on $S = \ kiri \ {x \ dalam \ mathbb {R}, x> 0 \ kanan \} $.

  $ {f} 'x = 1 + \ log x $

  $ {f} '' x = \ frac {1} {x}> 0 $

  Jadi, fungsi ini benar-benar cembung.

• $ f \ left (x \ right) = e ^ {x}, x \ in \ mathbb {R} $ benar-benar cembung.

Misalkan $ f: S \ rightarrow \ mathbb {R}$ where $S \ subset \ mathbb {R} ^ n$ is a non-empty convex set. The function f is said to be quasiconvex if for each $x_1, x_2 \ dalam S$, we have $f \ kiri (\ lambda x_1 + \ kiri (1- \ lambda \ kanan) x_2 \ kanan) \ leq max \ kiri \ {f \ kiri (x_1 \ kanan), f \ kiri (x_2 \ kanan) \ kanan \}, \ lambda \ in \ left (0, 1 \ kanan) $

Misalnya, $ f \ left (x \ right) = x ^ {3} $

Misalkan $ f: S \ rightarrow R $ where $S \ subset \ mathbb {R} ^ n$ is a non-empty convex set. The function f is said to be quasiconvex if for each $x_1, x_2 \ dalam S$, we have $f \ kiri (\ lambda x_1 + \ kiri (1- \ lambda \ kanan) x_2 \ kanan) \ geq min \ kiri \ {f \ kiri (x_1 \ kanan), f \ kiri (x_2 \ kanan) \ kanan \}, \ lambda \ in \ left (0, 1 \ kanan) $

Catatan

• Setiap fungsi cembung adalah quasiconvex tetapi kebalikannya tidak benar.
• Sebuah fungsi yang quasiconvex dan quasiconcave disebut quasimonotone.

Dalil

Misalkan $ f: S \ rightarrow \ mathbb {R}$ and S is a non empty convex set in $\ mathbb {R} ^ n$. The function f is quasiconvex if and only if $S _ {\ alpha} = \ kiri (x \ di S: f \ kiri (x \ kanan) \ leq \ alpha \ kanan \}$ is convex for each real number \alpha$

Bukti

Misalkan f adalah quasiconvex pada S.

Membiarkan $x_1,x_2 \in S_{\alpha}$ karena itu $x_1,x_2 \in S$ dan $max \left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \}\leq \alpha$

Membiarkan $\lambda \in \left (0, 1 \right )$ dan biarkan $x=\lambda x_1+\left ( 1-\lambda \right )x_2\leq max \left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \}\Rightarrow x \in S$

Jadi, $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq max\left \{ f\left ( x_1 \right ), f\left ( x_2 \right ) \right \}\leq \alpha$

Karena itu, $S_{\alpha}$ adalah cembung.

Berbicara

Membiarkan $S_{\alpha}$ adalah cembung untuk masing-masing $\alpha$

$x_1,x_2 \in S, \lambda \in \left ( 0,1\right )$

$x=\lambda x_1+\left ( 1-\lambda \right )x_2$

Membiarkan $x=\lambda x_1+\left ( 1-\lambda \right )x_2$

Untuk $x_1, x_2 \in S_{\alpha}, \alpha= max \left \{ f\left ( x_1 \right ), f\left ( x_2 \right ) \right \}$

$\Rightarrow \lambda x_1+\left (1-\lambda \right )x_2 \in S_{\alpha}$

$\Rightarrow f \left (\lambda x_1+\left (1-\lambda \right )x_2 \right )\leq \alpha$

Karenanya terbukti.

Dalil

Membiarkan $f:S\rightarrow \mathbb{R}$ dan S adalah himpunan konveks yang tidak kosong $\mathbb{R}^n$. Fungsi f adalah quasiconcave jika dan hanya jika$S_{\alpha} =\left \{ x \in S:f\left ( x \right )\geq \alpha \right \}$ adalah cembung untuk setiap bilangan real $\alpha$.

Dalil

Membiarkan $f:S\rightarrow \mathbb{R}$ dan S adalah himpunan konveks yang tidak kosong $\mathbb{R}^n$. Fungsi f adalah quasimonotone jika dan hanya jika$S_{\alpha} =\left \{ x \in S:f\left ( x \right )= \alpha \right \}$ adalah cembung untuk setiap bilangan real $\alpha$.

Dalil

Misalkan S adalah cembung yang tidak kosong $\mathbb{R}^n$ dan $f:S \rightarrow \mathbb{R}$ dapat dibedakan pada S, maka f adalah quasiconvex jika dan hanya jika ada $x_1,x_2 \in S$ dan $f\left ( x_1 \right )\leq f\left ( x_2 \right )$, kita punya $\bigtriangledown f\left ( x_2 \right )^T\left ( x_2-x_1 \right )\leq 0$

Bukti

Misalkan f menjadi fungsi quasiconvex.

Membiarkan $x_1,x_2 \in S$ seperti yang $f\left ( x_1 \right ) \leq f\left ( x_2 \right )$

Dengan diferensiabilitas f at $x_2, \lambda \in \left ( 0, 1 \right )$

$f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )=f\left ( x_2+\lambda \left (x_1-x_2 \right ) \right )=f\left ( x_2 \right )+\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )$

$+\lambda \left \| x_1-x_2 \right \|\alpha \left ( x_2,\lambda \left ( x_1-x_2 \right ) \right )$

$\Rightarrow f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )-f\left ( x_2 \right )-f\left ( x_2 \right )=\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )$

$+\lambda \left \| x_1-x_2 \right \|\alpha \left ( x2, \lambda\left ( x_1-x_2 \right )\right )$

Tapi karena f adalah quasiconvex, $f \left ( \lambda x_1+ \left ( 1- \lambda \right )x_2 \right )\leq f \left (x_2 \right )$

$\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )+\lambda \left \| x_1-x_2 \right \|\alpha \left ( x_2,\lambda \left ( x_1,x_2 \right ) \right )\leq 0$

Tapi $\alpha \left ( x_2,\lambda \left ( x_1,x_2 \right )\right )\rightarrow 0$ sebagai $\lambda \rightarrow 0$

Karena itu, $\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right ) \leq 0$

Berbicara

biarkan $x_1,x_2 \in S$ dan $f\left ( x_1 \right )\leq f\left ( x_2 \right )$, $\bigtriangledown f\left ( x_2 \right )^T \left ( x_1,x_2 \right ) \leq 0$

Untuk menunjukkan bahwa f adalah quasiconvex, yaitu $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq f\left ( x_2 \right )$

Proof by contradiction

Misalkan ada $x_3= \lambda x_1+\left ( 1-\lambda \right )x_2$ sedemikian rupa sehingga $ f \ left (x_2 \ right) <f \ left (x_3 \ right) $ untuk beberapa $ \lambda \in \left ( 0, 1 \right )$

Untuk $x_2$ dan $x_3,\bigtriangledown f\left ( x_3 \right )^T \left ( x_2-x_3 \right ) \leq 0$

$\Rightarrow -\lambda \bigtriangledown f\left ( x_3 \right )^T\left ( x_2-x_3 \right )\leq 0$

$\Rightarrow \bigtriangledown f\left ( x_3 \right )^T \left ( x_1-x_2 \right )\geq 0$

Untuk $x_1$ dan $x_3,\bigtriangledown f\left ( x_3 \right )^T \left ( x_1-x_3 \right ) \leq 0$

$\Rightarrow \left ( 1- \lambda \right )\bigtriangledown f\left ( x_3 \right )^T\left ( x_1-x_2 \right )\leq 0$

$\Rightarrow \bigtriangledown f\left ( x_3 \right )^T \left ( x_1-x_2 \right )\leq 0$

jadi, dari persamaan di atas, $\bigtriangledown f\left ( x_3 \right )^T \left ( x_1-x_2 \right )=0$

Menetapkan $U=\left \{ x:f\left ( x \right )\leq f\left ( x_2 \right ),x=\mu x_2+\left ( 1-\mu \right )x_3, \mu \in \left ( 0,1 \right ) \right \}$

Demikianlah yang bisa kita temukan $x_0 \in U$ seperti yang $x_0 = \mu_0 x_2= \mu x_2+\left ( 1- \mu \right )x_3$ untuk beberapa $\mu _0 \in \left ( 0,1 \right )$ yang terdekat dengan $x_3$ dan $\hat{x} \in \left ( x_0,x_1 \right )$ sedemikian rupa sehingga dengan teorema nilai rata-rata,

$$\frac{f\left ( x_3\right )-f\left ( x_0\right )}{x_3-x_0}= \bigtriangledown f\left ( \hat{x}\right )$$

$$\Rightarrow f\left ( x_3 \right )=f\left ( x_0 \right )+\bigtriangledown f\left ( \hat{x} \right )^T\left ( x_3-x_0 \right )$$

$$\Rightarrow f\left ( x_3 \right )=f\left ( x_0 \right )+\mu_0 \lambda f\left ( \hat{x}\right )^T \left ( x_1-x_2 \right )$$

Sejak $x_0$ adalah kombinasi dari $x_1$ dan $x_2$ dan $ f \ left (x_2 \ right) <f \ left (\ hat {x} \ right) $

Dengan mengulangi prosedur awal, $\bigtriangledown f \left ( \hat{x}\right )^T \left ( x_1-x_2\right )=0$

Jadi, dengan menggabungkan persamaan di atas, kita mendapatkan:

$$f\left ( x_3\right )=f\left ( x_0 \right ) \leq f\left ( x_2\right )$$

$$\Rightarrow f\left ( x_3\right )\leq f\left ( x_2\right )$$

Karenanya, ini adalah kontradiksi.

Contoh

Step 1 - $f\left ( x\right )=X^3$

$Let f \left ( x_1\right )\leq f\left ( x_2\right )$

$\Rightarrow x_{1}^{3}\leq x_{2}^{3}\Rightarrow x_1\leq x_2$

$\bigtriangledown f\left ( x_2 \right )\left ( x_1-x_2 \right )=3x_{2}^{2}\left ( x_1-x_2 \right )\leq 0$

Jadi, $f\left ( x\right )$ adalah quasiconvex.

Step 2 - $f\left ( x\right )=x_{1}^{3}+x_{2}^{3}$

Membiarkan $\hat{x_1}=\left ( 2, -2\right )$ dan $\hat{x_2}=\left ( 1, 0\right )$

jadi, $ f \ left (\ hat {x_1} \ right) = 0, f \ left (\ hat {x_2} \ right) = 1 \ Rightarrow f \ left (\ hat {x_1} \ right) \ setminus <f \ kiri (\ hat {x_2} \ kanan) $

Jadi, $\bigtriangledown f \left ( \hat{x_2}\right )^T \left ( \hat{x_1}- \hat{x_2}\right )= \left ( 3, 0\right )^T \left ( 1, -2\right )=3 >0$

Karenanya $f\left ( x\right )$ bukan quasiconvex.

Membiarkan $f:S\rightarrow \mathbb{R}^n$ dan S adalah set konveks yang tidak kosong $\mathbb{R}^n$ maka f dikatakan sebagai fungsi kuasicovex jika untuk masing-masing $x_1,x_2 \in S$ dengan $f\left ( x_1 \right ) \neq f\left ( x_2 \right )$, kita memiliki $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) <max \: \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ kanan \} $

Catatan

• Setiap fungsi quasiconvex ketat bersifat konveks.
• Fungsi quasiconvex ketat tidak berarti quasiconvexity.
• Fungsi quasiconvex ketat mungkin bukan quasiconvex kuat.
• Fungsi pseudoconvex adalah fungsi quasiconvex yang ketat.

Dalil

Membiarkan $f:S\rightarrow \mathbb{R}^n$ menjadi fungsi quasiconvex ketat dan S menjadi cembung non-kosong yang disetel $\mathbb{R}^n$Pertimbangkan masalahnya: $min \:f\left ( x \right ), x \in S$. Jika$\hat{x}$ adalah solusi optimal lokal $\bar{x}$ adalah solusi optimal global.

Bukti

Biarkan ada $ \bar{x} \in S$ seperti yang $f\left ( \bar{x}\right )\leq f \left ( \hat{x}\right )$

Sejak $\bar{x},\hat{x} \in S$ dan S adalah himpunan cembung, oleh karena itu,

$$\lambda \bar{x}+\left ( 1-\lambda \right )\hat{x}\in S, \forall \lambda \in \left ( 0,1 \right )$$

Sejak $\hat{x}$ adalah minima lokal, $f\left ( \hat{x} \right ) \leq f\left ( \lambda \bar{x}+\left ( 1-\lambda \right )\hat{x} \right ), \forall \lambda \in \left ( 0,\delta \right )$

Karena f sangat quasiconvex.

$$ f \ left (\ lambda \ bar {x} + \ left (1- \ lambda \ right) \ hat {x} \ kanan) <max \ left \ {f \ left (\ hat {x} \ kanan) , f \ kiri (\ bar {x} \ kanan) \ kanan \} = f \ kiri (\ topi {x} \ kanan) $$

Karenanya, ini adalah kontradiksi.

Fungsi quasiconcave yang ketat

Membiarkan $f:S\rightarrow \mathbb{R}^n$ dan S adalah set konveks yang tidak kosong $\mathbb{R}^n$, maka f saud menjadi fungsi kuasicovex ketat jika untuk masing-masing $x_1,x_2 \in S$ dengan $f\left (x_1\right )\neq f\left (x_2\right )$, kita punya

$$f\left (\lambda x_1+\left (1-\lambda\right )x_2\right )> min \left \{ f \left (x_1\right ),f\left (x_2\right )\right \}$$.

Contoh

• $f\left (x\right )=x^2-2$

  Ini adalah fungsi quasiconvex ketat karena jika kita mengambil dua poin $x_1,x_2$ dalam domain yang memenuhi batasan dalam definisi $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) <max \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ right \} $ Karena fungsinya menurun pada sumbu x negatif dan fungsinya meningkat pada sumbu x positif (karena ini adalah parabola).

• $f\left (x\right )=-x^2$

  Ini bukan fungsi quasiconvex ketat karena jika kita ambil $x_1=1$ dan $x_2=-1$ dan $\lambda=0.5$, kemudian $f\left (x_1\right )=-1=f\left (x_2\right )$ tapi $f\left (\lambda x_1+\left (1- \lambda\right )x_2\right )=0$Oleh karena itu, ia tidak memenuhi kondisi yang disebutkan dalam definisi. Tetapi ini adalah fungsi quasiconcave karena jika kita mengambil dua titik dalam domain yang memenuhi batasan dalam definisi$f\left ( \lambda x_1+\left (1-\lambda\right )x_2\right )> min \left \{ f \left (x_1\right ),f\left (x_2\right )\right \}$. Karena fungsinya meningkat pada sumbu x negatif dan fungsinya menurun pada sumbu x positif.

Membiarkan $f:S\rightarrow \mathbb{R}^n$ dan S adalah set konveks yang tidak kosong $\mathbb{R}^n$ maka f adalah fungsi quasiconvex kuat jika ada $x_1,x_2 \in S$ dengan $\left ( x_1 \right ) \neq \left ( x_2 \right )$, kita memiliki $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) <max \: \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ kanan \}, \ depan \ lambda \ dalam \ kiri (0,1 \ kanan) $

Dalil

Fungsi quasiconvex $f:S\rightarrow \mathbb{R}^n$ pada cembung yang tidak kosong set S in $\mathbb{R}^n$ adalah fungsi quasiconvex kuat jika tidak konstan pada segmen garis yang menghubungkan titik S.

Bukti

Misal f adalah fungsi quasiconvex dan tidak konstan pada ruas garis yang menghubungkan titik-titik S.

Misalkan f bukanlah fungsi quasiconvex yang kuat.

Terdapat $x_1,x_2 \in S$ dengan $x_1 \neq x_2$ seperti yang

$$f\left ( z \right )\geq max\left \{ f\left ( x_1 \right ), f\left ( x_2 \right ) \right \}, \forall z= \lambda x_1+\left ( 1-\lambda \right )x_2, \lambda \in \left ( 0,1 \right )$$

$\Rightarrow f\left ( x_1 \right )\leq f\left ( z \right )$ dan $f\left ( x_2 \right )\leq f\left ( z \right )$

Karena f tidak konstan dalam $\left [ x_1,z \right ]$ dan $\left [z,x_2 \right ] $

Jadi ada $u \in \left [ x_1,z \right ]$ dan $v=\left [ z,x_2 \right ]$

$$\Rightarrow u= \mu_1x_1+\left ( 1-\mu_1\right )z,v=\mu_2z+\left ( 1- \mu_2\right )x_2$$

Karena f adalah quasiconvex,

$$\Rightarrow f\left ( u \right )\leq max\left \{ f\left ( x_1 \right ),f \left ( z \right ) \right \}=f\left ( z \right )\:\: and \:\:f \left ( v \right ) \leq max \left \{ f\left ( z \right ),f\left ( x_2 \right ) \right \}$$

$$\Rightarrow f\left ( u \right )\leq f\left ( z \right ) \:\: and \:\: f\left ( v \right )\leq f\left ( z \right )$$

$$\Rightarrow max \left \{ f\left ( u \right ),f\left ( v \right ) \right \} \leq f\left ( z \right )$$

Tetapi z adalah titik mana pun antara u dan v, jika ada yang sama, maka f konstan.

Karena itu, $max \left \{ f\left ( u \right ),f\left ( v \right ) \right \} \leq f\left ( z \right )$

yang bertentangan dengan quasiconvexity dari f as $z \in \left [ u,v \right ]$.

Oleh karena itu f adalah fungsi kuasikonveks kuat.

Dalil

Membiarkan $f:S\rightarrow \mathbb{R}^n$ dan S adalah set konveks yang tidak kosong $\mathbb{R}^n$. Jika$\hat{x}$ adalah solusi optimal lokal $\hat{x}$ adalah solusi optimal global yang unik.

Bukti

Karena fungsi quasiconvex yang kuat juga merupakan fungsi quasiconvex yang ketat, maka solusi optimal lokal adalah solusi optimal global.

Uniqueness - Biarkan f mencapai solusi optimal global di dua titik $u,v \in S$

$$\Rightarrow f\left ( u \right ) \leq f\left ( x \right ).\forall x \in S\:\: and \:\:f\left ( v \right ) \leq f\left ( x \right ).\forall x \in S$$

Jika Anda adalah solusi optimal global, $f\left ( u \right )\leq f\left ( v \right )$ dan $f\left ( v \right )\leq f\left ( u\right )\Rightarrow f\left ( u \right )=f\left ( v\right )$

$$ f \ kiri (\ lambda u + \ kiri (1- \ lambda \ kanan) v \ kanan) <max \ kiri \ {f \ kiri (u \ kanan), f \ kiri (v \ kanan) \ kanan \} = f \ kiri (u \ kanan) $$

yang merupakan kontradiksi.

Karenanya, hanya ada satu solusi optimal global.

Catatan

• Fungsi quasiconvex yang kuat juga merupakan fungsi quasiconvex yang ketat.
• Fungsi yang sangat cembung mungkin atau mungkin tidak quasiconvex kuat.
• Cembung ketat yang dapat dibedakan adalah kuasikonveks kuat.

Membiarkan $f:S\rightarrow \mathbb{R}$ menjadi fungsi yang dapat dibedakan dan S menjadi himpunan konveks yang tidak kosong $\mathbb{R}^n$, maka f dikatakan pseudoconvex jika untuk masing-masing $x_1,x_2 \in S$ dengan $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\geq 0$, kita punya $f\left ( x_2 \right )\geq f\left ( x_1 \right )$, atau setara jika $f\left ( x_1 \right )>f\left ( x_2 \right )$ lalu $ \ bigtriangledown f \ left (x_1 \ right) ^ T \ left (x_2-x_1 \ right) <0 $

Fungsi pseudoconcave

Membiarkan $f:S\rightarrow \mathbb{R}$ menjadi fungsi yang dapat dibedakan dan S menjadi himpunan konveks yang tidak kosong $\mathbb{R}^n$, maka f dikatakan pseudoconvex jika untuk masing-masing $x_1, x_2 \in S$ dengan $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\geq 0$, kita punya $f\left ( x_2 \right )\leq f\left ( x_1 \right )$, atau setara jika $f\left ( x_1 \right )>f\left ( x_2 \right )$ kemudian $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )>0$

Catatan

• Jika suatu fungsi adalah pseudoconvex dan pseudoconcave, maka disebut pseudolinear.

• Fungsi cembung yang dapat dibedakan juga disebut pseudokonveks.

• Fungsi pseudoconvex mungkin tidak cembung. Sebagai contoh,

  $f\left ( x \right )=x+x^3$tidak cembung. Jika$x_1 \leq x_2,x_{1}^{3} \leq x_{2}^{3}$

  Jadi,$\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )=\left ( 1+3x_{1}^{2} \right )\left ( x_2-x_1 \right ) \geq 0$

  Dan, $f\left ( x_2 \right )-f\left ( x_1 \right )=\left ( x_2-x_1 \right )+\left ( x_{2}^{3} -x_{1}^{3}\right )\geq 0$

  $\Rightarrow f\left ( x_2 \right )\geq f\left ( x_1 \right )$

  Jadi, itu adalah pseudoconvex.

  Fungsi pseudoconvex secara ketat adalah quasiconvex. Jadi, setiap minimum lokal pseudoconvex juga minimum global.

Fungsi pseudoconvex yang ketat

Membiarkan $f:S\rightarrow \mathbb{R}$ menjadi fungsi yang dapat dibedakan dan S menjadi himpunan konveks yang tidak kosong $\mathbb{R}^n$, maka f dikatakan pseudoconvex jika untuk masing-masing $x_1,x_2 \in S$ dengan $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\geq 0$, kita punya $f\left ( x_2 \right )> f\left ( x_1 \right )$, atau setara jika $f\left ( x_1 \right )\geq f\left ( x_2 \right )$ lalu $ \ bigtriangledown f \ left (x_1 \ right) ^ T \ left (x_2-x_1 \ right) <0 $

Dalil

Misalkan f adalah fungsi pseudoconvex dan anggaplah $\bigtriangledown f\left ( \hat{x}\right )=0$ untuk beberapa $\hat{x} \in S$, kemudian $\hat{x}$ adalah solusi optimal global dari f over S.

Bukti

Membiarkan $\hat{x}$ menjadi titik kritis dari f, yaitu, $\bigtriangledown f\left ( \hat{x}\right )=0$

Karena f adalah fungsi pseudoconvex, untuk $x \in S,$ kita punya

$$\bigtriangledown f\left ( \hat{x}\right )\left ( x-\hat{x}\right )=0 \Rightarrow f\left ( \hat{x}\right )\leq f\left ( x\right ), \forall x \in S$$

Karenanya, $\hat{x}$ adalah solusi optimal global.

Ucapan

Jika f adalah fungsi pseudoconvex ketat, $\hat{x}$ adalah solusi optimal global yang unik.

Dalil

Jika f adalah fungsi pseudokonveks yang dapat dibedakan atas S, maka f adalah fungsi kuasikonveks dan kuasikonveks.

Catatan

• Jumlah dari dua fungsi pseudokonveks yang ditentukan pada himpunan S terbuka $\mathbb{R}^n$ mungkin bukan pseudoconvex.

• Membiarkan $f:S\rightarrow \mathbb{R}$ menjadi fungsi quasiconvex dan S menjadi subset konveks yang tidak kosong dari $\mathbb{R}^n$ maka f adalah pseudoconvex jika dan hanya jika setiap titik kritis adalah minimum global f atas S.

• Misalkan S adalah subset cembung yang tidak kosong dari $\mathbb{R}^n$ dan $f:S\rightarrow \mathbb{R}$ menjadi fungsi seperti itu $\bigtriangledown f\left ( x\right )\neq 0$ untuk setiap $x \in S$ maka f adalah pseudoconvex jika dan hanya jika itu adalah fungsi quasiconvex.

Ada empat jenis masalah pemrograman cembung -

Step 1 - $min \:f\left ( x \right )$, dimana $x \in S$ dan S adalah set konveks yang tidak kosong $\mathbb{R}^n$ dan $f\left ( x \right )$ adalah fungsi cembung.

Step 2 - $min \: f\left ( x \right ), x \in \mathbb{R}^n$ tunduk pada

$g_i\left ( x \right ) \geq 0, 1 \leq m_1$ dan $g_i\left ( x \right )$ adalah fungsi cembung.

$g_i\left ( x \right ) \leq 0,m_1+1 \leq m_2$ dan $g_i\left ( x \right )$ adalah fungsi cekung.

$g_i\left ( x \right ) = 0, m_2+1 \leq m$ dan $g_i\left ( x \right )$ adalah fungsi linier.

dimana $f\left ( x \right )$ adalah fucntion cembung.

Step 3 - $max \:f\left ( x \right )$ dimana $x \in S$ dan S adalah set konveks yang tidak kosong $\mathbb{R}^n$ dan $f\left ( x \right )$ adalah fungsi cekung.

Step 4 - $min \:f\left ( x \right )$, dimana $x \in \mathbb{R}^n$ tunduk pada

$g_i\left ( x \right ) \geq 0, 1 \leq m_1$ dan $g_i\left ( x \right )$ adalah fungsi cembung.

$g_i\left ( x \right ) \leq 0, m_1+1 \leq m_2$ dan $g_i\left ( x \right )$ adalah fungsi cekung.

$g_i\left ( x \right ) = 0,m_2+1 \leq m$ dan $g_i\left ( x \right )$ adalah fungsi linier.

dimana $f\left ( x \right )$ adalah fungsi cekung.

Kerucut arah yang layak

Misalkan S menjadi himpunan yang tidak kosong di $\mathbb{R}^n$ dan biarkan $\hat{x} \in \:Closure\left ( S \right )$, maka kerucut arah yang layak dari S at $\hat{x}$, dilambangkan dengan D, didefinisikan sebagai $D=\left \{ d:d\neq 0,\hat{x}+\lambda d \in S, \lambda \in \left ( 0, \delta \right ), \delta > 0 \right \}$

Setiap vektor bukan nol $d \in D$ disebut arah yang layak.

Untuk fungsi tertentu $f:\mathbb{R}^n \Rightarrow \mathbb{R}$ kerucut meningkatkan arah di $\hat{x}$ dilambangkan dengan F dan diberikan oleh

$$F=\left \{ d:f\left ( \hat{x}+\lambda d \right )\leq f\left ( \hat{x} \right ),\forall \lambda \in \left ( 0,\delta \right ), \delta >0 \right \}$$

Setiap arah $d \in F$ disebut arah perbaikan atau arah penurunan f at $\hat{x}$

Dalil

Necessary Condition

Pertimbangkan masalahnya $min f\left ( x \right )$ seperti yang $x \in S$ dimana S adalah himpunan yang tidak kosong $\mathbb{R}^n$. Misalkan f dapat terdiferensiasi pada suatu titik$\hat{x} \in S$. Jika$\hat{x}$ adalah solusi optimal lokal $F_0 \cap D= \phi$ di mana $ F_0 = \ left \ {d: \ bigtriangledown f \ left (\ hat {x} \ right) ^ T d <0 \ right \} $ dan D adalah kerucut arah yang memungkinkan.

Sufficient Condition

Jika $F_0 \cap D= \phi$ f adalah fungsi pseudoconvex di $\hat{x}$ dan ada lingkungan sekitar $\hat{x},N_\varepsilon \left ( \hat{x} \right ), \varepsilon > 0$ seperti yang $d=x-\hat{x}\in D$ untuk apapun $x \in S \cap N_\varepsilon \left ( \hat{x} \right )$, kemudian $\hat{x}$ adalah solusi optimal lokal.

Bukti

Necessary Condition

Membiarkan $F_0 \cap D\neq \phi$, yaitu, ada a $d \in F_0 \cap D$ seperti yang $d \in F_0$ dan $d\in D$

Sejak $d \in D$, oleh karena itu ada $\delta_1 >0$ seperti yang $\hat{x}+\lambda d \in S, \lambda \in \left ( 0,\delta_1 \right ).$

Sejak $d \in F_0$, oleh karena itu $ \ bigtriangledown f \ left (\ hat {x} \ right) ^ T d <0 $

Jadi, ada $\delta_2>0$ sedemikian rupa sehingga $ f \ left (\ hat {x} + \ lambda d \ right) <f \ left (\ hat {x} \ right), \ forall \ lambda \ in f \ left (0, \ delta_2 \ right) $

Membiarkan $\delta=min \left \{\delta_1,\delta_2 \right \}$

Kemudian $ \ hat {x} + \ lambda d \ in S, f \ left (\ hat {x} + \ lambda d \ right) <f \ left (\ hat {x} \ right), \ forall \ lambda \ di f \ kiri (0, \ delta \ kanan) $

Tapi $\hat{x}$ adalah solusi optimal lokal.

Oleh karena itu, kontradiksi.

Jadi $F_0\cap D=\phi$

Sufficient Condition

Membiarkan $F_0 \cap D\neq \phi$ dan biarkan f menjadi fungsi pseudoconvex.

Biarkan ada lingkungan $\hat{x}, N_{\varepsilon}\left ( \hat{x} \right )$ seperti yang $d=x-\hat{x}, \forall x \in S \cap N_\varepsilon\left ( \hat{x} \right )$

Membiarkan $\hat{x}$ bukanlah solusi optimal lokal.

Jadi, ada $\bar{x} \in S \cap N_\varepsilon \left ( \hat{x} \right )$ sedemikian rupa sehingga $ f \ left (\ bar {x} \ right) <f \ left (\ hat {x} \ right) $

Dengan asumsi $S \cap N_\varepsilon \left ( \hat{x} \right ),d=\left ( \bar{x}-\hat{x} \right )\in D$

Dengan pseudoconvex dari f,

$$ f \ left (\ hat {x} \ right)> f \ left (\ bar {x} \ right) \ Rightarrow \ bigtriangledown f \ left (\ hat {x} \ kanan) ^ T \ kiri (\ bar {x} - \ hat {x} \ kanan) <0 $$

$ \ Rightarrow \ bigtriangledown f \ left (\ hat {x} \ right) ^ T d <0 $

$\Rightarrow d \in F_0$

karenanya $F_0\cap D \neq \phi$

yang merupakan kontradiksi.

Karenanya, $\hat{x}$ adalah solusi optimal lokal.

Pertimbangkan masalah berikut ini:$min \:f\left ( x\right )$ dimana $x \in X$ seperti yang $g_x\left ( x\right ) \leq 0, i=1,2,...,m$

$f:X \rightarrow \mathbb{R},g_i:X \rightarrow \mathbb{R}^n$ dan X adalah set terbuka $\mathbb{R}^n$

Membiarkan $S=\left \{x:g_i\left ( x\right )\leq 0,\forall i \right \}$

Membiarkan $\hat{x} \in X$, kemudian $M=\left \{1,2,...,m \right \}$

Membiarkan $I=\left \{i:g_i\left ( \hat{x}\right )=0, i \in M\right \}$ di mana saya disebut set indeks untuk semua kendala aktif di $\hat{x}$

Misalkan $ J = \ left \ {i: g_i \ left (\ hat {x} \ right) <0, i \ in M ​​\ right \} $ di mana J disebut himpunan indeks untuk semua batasan aktif di $\hat{x}$.

Misalkan $ F_0 = \ kiri \ {d \ in \ mathbb {R} ^ m: \ bigtriangledown f \ left (\ hat {x} \ right) ^ T d <0 \ right \} $

Misalkan $ G_0 = \ kiri \ {d \ in \ mathbb {R} ^ m: \ bigtriangledown gI \ left (\ hat {x} \ right) ^ T d <0 \ right \} $

atau $ G_0 = \ left \ {d \ in \ mathbb {R} ^ m: \ bigtriangledown gi \ left (\ hat {x} \ right) ^ T d <0, \ forall i \ in I \ right \} $

Kata pengantar singkat

Jika $S=\left \{ x \in X:g_i\left ( x\right ) \leq 0, \forall i \in I\right \}$ dan X adalah set terbuka tidak kosong $\mathbb{R}^n$. Membiarkan$\hat{x}\in S$ dan $g_i$ berbeda di $\hat{x}, i \in I$ dan biarkan $g_i$ dimana $i \in J$ kontinu di $\hat{x}$, kemudian $G_0 \subseteq D$.

Bukti

Membiarkan $d \in G_0$

Sejak $\hat{x} \in X$ dan X adalah himpunan terbuka, jadi ada $\delta_1 >0$ seperti yang $\hat{x}+\lambda d \in X$ untuk $\lambda \in \left ( 0, \delta_1\right )$

Juga karena $ g_ \ hat {x} <0 $ dan $g_i$ kontinu di $\hat{x}, \forall i \in J$, disana ada $\delta_2>0$, $ g_i \ left (\ hat {x} + \ lambda d \ right) <0, \ lambda \ in \ left (0, \ delta_2 \ kanan) $

Sejak $d \in G_0$, oleh karena itu, $ \ bigtriangledown g_i \ left (\ hat {x} \ right) ^ T d <0, \ forall i \ in I $ sehingga ada $ \ delta_3> 0, g_i \ left (\ hat {x} + \ lambda d \ right) <g_i \ left (\ hat {x} \ right) = 0 $, untuk $\lambda \in \left ( 0, \delta_3\right ) i \in J$

Membiarkan $\delta=min\left \{ \delta_1, \delta_2, \delta_3 \right \}$

oleh karena itu, $ \ hat {x} + \ lambda d \ in X, g_i \ left (\ hat {x} + \ lambda d \ right) <0, i \ in M ​​$

$\Rightarrow \hat{x}+\lambda d \in S$

$\Rightarrow d \in D$

$\Rightarrow G_0 \subseteq D$

Oleh karena itu Terbukti.

Dalil

Necessary Condition

Membiarkan $f$ dan $g_i, i \in I$, berbeda di $\hat{x} \in S,$ dan $g_j$ terus di $\hat{x} \in S$. Jika$\hat{x}$ adalah minimum lokal $S$, kemudian $F_0 \cap G_0=\phi$.

Sufficient Condition

Jika $F_0 \cap G_0= \phi$ dan f adalah fungsi pseudoconvex di $\left (\hat{x}, g_i 9x \right ), i \in I$ adalah fungsi pseudoconvex ketat di beberapa $\varepsilon$ - lingkungan $\hat{x}, \hat{x}$ adalah solusi optimal lokal.

Catatan

• Membiarkan $\hat{x}$ menjadi titik yang layak seperti itu $\bigtriangledown f\left(\hat{x} \right)=0$, kemudian $F_0 = \phi$. Jadi,$F_0 \cap G_0= \phi$ tapi $\hat{x}$ bukanlah solusi yang optimal

• Tapi jika $\bigtriangledown g\left(\hat{x} \right)=0$, kemudian $G_0=\phi$, jadi $F_0 \cap G_0= \phi$

• Pertimbangkan masalahnya: min $f\left(x \right)$ seperti yang $g\left(x \right)=0$.

  Sejak $g\left(x \right)=0$, jadi $ g_1 \ left (x \ right) = g \ left (x \ right) <0 $ dan $g_2\left(x \right)=-g\left(x \right) \leq 0$.

  Membiarkan $\hat{x} \in S$, kemudian $g_1\left(\hat{x} \right)=0$ dan $g_2\left(\hat{x} \right)=0$.

  Tapi $\bigtriangledown g_1\left(\hat{x} \right)= - \bigtriangledown g_2\left(\hat{x}\right)$

  Jadi, $G_0= \phi$ dan $F_0 \cap G_0= \phi$.

Kondisi yang Diperlukan

Dalil

Pertimbangkan masalahnya - $min f\left ( x \right )$ seperti yang $x \in X$ di mana X adalah set terbuka $\mathbb{R}^n$ dan biarkan $g_i \left ( x \right ) \leq 0, \forall i =1,2,....m$.

Membiarkan $f:X \rightarrow \mathbb{R}$ dan $g_i:X \rightarrow \mathbb{R}$

Membiarkan $\hat{x}$ menjadi solusi yang layak dan biarkan f dan $g_i, i \in I$ dibedakan di $\hat{x}$ dan $g_i, i \in J$ kontinu di $\hat{x}$.

Jika $\hat{x}$ memecahkan masalah di atas secara lokal, lalu ada $u_0, u_i \in \mathbb{R}, i \in I$ seperti yang $u_0 \bigtriangledown f\left ( \hat{x} \right )+\displaystyle\sum\limits_{i\in I} u_i \bigtriangledown g_i \left ( \hat{x} \right )$= 0

dimana $u_0,u_i \geq 0,i \in I$ dan $\left ( u_0, u_I \right ) \neq \left ( 0,0 \right )$

Selanjutnya jika $g_i,i \in J$ juga dapat dibedakan di $\hat{x}$, maka ketentuan di atas dapat ditulis sebagai -

$u_0 \bigtriangledown f\left ( \hat{x}\right )+\displaystyle\sum\limits_{i=1}^m u_i \bigtriangledown g_i\left ( \hat{x} \right )=0$

$u_ig_i\left (\hat{x} \right )$= 0

$u_0,u_i \geq 0, \forall i=1,2,....,m$

$\left (u_0,u \right ) \neq \left ( 0,0 \right ), u=\left ( u_1,u_2,s,u_m \right ) \in \mathbb{R}^m$

Catatan

• $u_i$ disebut pengganda Lagrangian.

• Kondisi itu $\hat{x}$ layak untuk masalah yang diberikan disebut kondisi layak primal.

• Yang dibutuhkan $u_0 \bigtriangledown f\left (\hat{x} \right )+\displaystyle\sum\limits_{i=1}^m u-i \bigtriangledown g_i\left ( x \right )=0$ disebut kondisi kelayakan ganda.

• Kondisi $u_ig_i\left ( \hat{x} \right )=0, i=1, 2, ...m$disebut kondisi kelambanan gratis. Kondisi ini membutuhkan$u_i=0, i \in J$

• Bersama kondisi kelayakan primal, kondisi kelayakan ganda dan kelambanan gratis disebut Kondisi Fritz-John.

Kondisi Cukup

Dalil

Jika ada $\varepsilon$-nighbourhood dari $\hat{x}N_\varepsilon \left ( \hat{x} \right ),\varepsilon >0$ sedemikian sehingga f pseudoconvex berakhir $N_\varepsilon \left ( \hat{x} \right )\cap S$ dan $g_i,i \in I$ benar-benar pseudoconvex berakhir $N_\varepsilon \left ( \hat{x}\right )\cap S$, kemudian $\hat{x}$adalah solusi optimal lokal untuk masalah yang dijelaskan di atas. Jika f adalah pseudoconvex pada$\hat{x}$ dan jika $g_i, i \in I$ keduanya merupakan fungsi pseudoconvex dan quasiconvex yang ketat di $\hat{x},\hat{x}$ adalah solusi optimal global untuk masalah yang dijelaskan di atas.

Contoh

• $min \:f\left ( x_1,x_2 \right )=\left ( x_1-3 \right )^2+\left ( x_2-2 \right )^2$

  seperti yang $x_{1}^{2}+x_{2}^{2} \leq 5, x_1+2x_2 \leq 4, x_1,x_2 \geq 0$ Dan $\hat{x}=\left ( 2,1 \right )$

  Membiarkan $g_1\left (x_1,x_2 \right )=x_{1}^{2}+x_{2}^{2} -5,$

  $g_2\left (x_1,x_2 \right )=x_1+2x_2-4,$

  $g_3\left (x_1,x_2 \right )=-x_1$ dan $g_4\left ( x_1, x_2 \right )= -x_2$.

  Dengan demikian kendala di atas dapat ditulis sebagai -

  $g_1\left (x_1,x_2 \right )\leq 0,$

  $g_2\left (x_1,x_2 \right )\leq 0,$

  $g_3\left (x_1,x_2 \right )\leq 0$ dan

  $g_4\left (x_1,x_2 \right )\leq 0$ Jadi, $I = \left \{1,2 \right \}$ karena itu, $u_3=0,u_4=0$

  $\bigtriangledown f \left (\hat{x} \right )=\left (2,-2 \right ),\bigtriangledown g_1\left (\hat{x} \right )=\left (4,2 \right )$ dan $\bigtriangledown g_2\left (\hat{x} \right )=\left (1,2 \right )$

  Jadi dengan menempatkan nilai-nilai ini pada kondisi pertama dari kondisi Fritz-John, kita dapatkan -

  $u_0=\frac{3}{2} u_2, \:\:u_1= \frac{1}{2}u_2,$ dan biarkan $u_2=1$, oleh karena itu $u_0= \frac{3}{2},\:\:u_1= \frac{1}{2}$

  Dengan demikian kondisi Fritz John terpenuhi.

• $min f\left (x_1,x_2\right )=-x_1$.

  seperti yang $x_2-\left (1-x_1\right )^3 \leq 0$,

  $-x_2 \leq 0$ dan $\hat{x}=\left (1,0\right )$

  Membiarkan $g_1\left (x_1,x_2 \right )=x_2-\left (1-x_1\right )^3$,

  $g_2\left (x_1,x_2 \right )=-x_2$

  Dengan demikian kendala di atas dapat dibuat sebagai -

  $g_1\left (x_1,x_2 \right )\leq 0,$

  $g_2\left (x_1,x_2 \right )\leq 0,$

  Jadi, $I=\left \{1,2 \right \}$

  $\bigtriangledown f\left (\hat{x} \right )=\left (-1,0\right )$

  $\bigtriangledown g_1 \left (\hat{x} \right )=\left (0,1\right )$ dan $g_2 \left (\hat{x} \right )=\left (0, -1 \right )$

  Jadi dengan menempatkan nilai-nilai ini pada kondisi pertama dari kondisi Fritz-John, kita dapatkan -

  $u_0=0,\:\: u_1=u_2=a>0$

  Dengan demikian kondisi Fritz John terpenuhi.

Pertimbangkan masalahnya -

$min \:f\left ( x \right )$ seperti yang $x \in X$, dengan X adalah set terbuka $\mathbb{R}^n$ dan $g_i \left ( x \right )\leq 0, i=1, 2,...,m$

Membiarkan $S=\left \{ x \in X:g_i\left ( x \right )\leq 0, \forall i \right \}$

Membiarkan $\hat{x} \in S$ dan biarkan $f$ dan $g_i,i \in I$ dibedakan di $\hat{x}$ dan $g_i, i \in J$ kontinu di $\hat{x}$. Selanjutnya,$\bigtriangledown g_i\left ( \hat{x} \right), i \in I$independen linier. Jika$\hat{x}$ memecahkan masalah di atas secara lokal, lalu ada $u_i,i \in I$ seperti yang

$\bigtriangledown f\left ( x\right)+\displaystyle\sum\limits_{i\in I} u_i \bigtriangledown g_i\left ( \hat{x} \right)=0$, $\:\:u_i \geq 0, i \in I$

Jika $g_i,i \in J$ juga dapat dibedakan di $\hat{x}$. kemudian$\hat{x}$, kemudian

$\bigtriangledown f\left ( \hat{x}\right)+\displaystyle\sum\limits_{i= 1}^m u_i \bigtriangledown g_i\left ( \hat{x} \right)=0$

$u_ig_i\left ( \hat{x} \right)=0, \forall i=1,2,...,m$

$u_i \geq 0 \forall i=1,2,...,m$

Contoh

Pertimbangkan masalah berikut -

$min \:f\left ( x_1,x_2 \right )=\left ( x_1-3\right )^2+\left ( x_2-2\right )^2$

seperti yang $x_{1}^{2}+x_{2}^{2}\leq 5$,

$x_1,2x_2 \geq 0$ dan $\hat{x}=\left ( 2,1 \right )$

Membiarkan $g_1\left ( x_1, x_2 \right)=x_{1}^{2}+x_{2}^{2}-5$,

$g_2\left ( x_1, x_2 \right)=x_{1}+2x_2-4$

$g_3\left ( x_1, x_2 \right)=-x_{1}$ dan $g_4\left ( x_1,x_2 \right )=-x_2$

Dengan demikian kendala di atas dapat ditulis sebagai -

$g_1 \left ( x_1,x_2 \right)\leq 0, g_2 \left ( x_1,x_2 \right) \leq 0$

$g_3 \left ( x_1,x_2 \right)\leq 0,$ dan $g_4 \left ( x_1,x_2 \right) \leq 0$ Jadi, $I=\left \{ 1,2 \right \}$ karena itu, $ u_3=0,\:\: u_4=0$

$\bigtriangledown f \left ( \hat{x} \right)=\left ( 2,-2 \right), \bigtriangledown g_1 \left ( \hat{x} \right)= \left ( 4,2 \right)$ dan

$\bigtriangledown g_2\left ( \hat{x} \right ) =\left ( 1,2 \right )$

Jadi dengan menempatkan nilai-nilai ini pada kondisi pertama dari kondisi Karush-Kuhn-Tucker, kita mendapatkan -

$u_1=\frac{1}{3}$ dan $u_2=\frac{2}{3}$

Dengan demikian kondisi Karush-Kuhn-Tucker terpenuhi.

Metode Penurunan Paling Curam

Metode ini juga disebut metode Gradien atau metode Cauchy. Metode ini melibatkan terminologi berikut -

$$x_{k+1}=x_k+\alpha_kd_k$$

$d_k= - \bigtriangledown f\left ( x_k \right )$ atau $ d_k= -\frac{\bigtriangledown f\left ( x_k \right )}{\left \| \bigtriangledown f\left ( x_k \right ) \right \|}$

Membiarkan $\phi \left (\alpha \right )=f\left ( x_k +\alpha d_k\right )$

Dengan membedakan $\phi$ dan menyamakannya dengan nol, kita bisa mendapatkannya $\alpha$.

Jadi algoritme berjalan sebagai berikut -

• Inisialisasi $x_0$,$\varepsilon_1$,$\varepsilon_2$ dan set $k=0$.

• Set $d_k=-\bigtriangledown f\left ( x_k \right ) $atau $d_k=-\frac{\bigtriangledown f\left (x_k \right )}{\left \|\bigtriangledown f\left (x_k \right ) \right \|}$.

• Temukan $\alpha_k$ sedemikian rupa sehingga meminimalkan $\phi\left ( \alpha \right )=f\left ( x_k+\alpha d_k \right )$.

• Set $x_{k+1}=x_k+\alpha_kd_k$.

• Jika $ \ meninggalkan \ | x_ {k + 1-x_k} \ kanan \ | <\ varepsilon_1 $ atau$\left \| \bigtriangledown f\left ( x_{k+1} \right ) \right \| \leq \varepsilon_2$, lanjutkan ke langkah 6, jika tidak disetel $k=k+1$ dan lanjutkan ke langkah 2.

• Solusi optimal adalah $\hat{x}=x_{k+1}$.

Metode Newton

Metode Newton bekerja berdasarkan prinsip berikut -

$f\left ( x \right )=y\left ( x \right )=f\left ( x_k \right )+\left ( x-x_k \right )^T \bigtriangledown f\left ( x_k \right )+\frac{1}{2}\left ( x-x_k \right )^T H\left ( x_k \right )\left ( x-x_k \right )$

$\bigtriangledown y\left ( x \right )=\bigtriangledown f\left ( x_k \right )+H\left ( x_k \right )\left ( x-x_k \right )$

Di $x_{k+1}, \bigtriangledown y\left ( x_{k+1} \right )=\bigtriangledown f\left ( x_k \right )+H\left ( x_k \right )\left ( x_{k+1}-x_k \right )$

Untuk $x_{k+1}$ menjadi solusi optimal $\bigtriangledown y\left ( x_k+1 \right )=0$

Jadi, $x_{k+1}=x_k-H\left ( x_k \right )^{-1} \bigtriangledown f\left ( x_k \right )$

Sini $H\left ( x_k \right )$ harus non-tunggal.

Karenanya algoritme berjalan sebagai berikut -

Step 1 - Inisialisasi $x_0,\varepsilon$ dan set $k=0$.

Step 2 - temukan $H\left ( x_k \right ) \bigtriangledown f\left ( x_k \right )$.

Step 3 - Pecahkan untuk sistem linier $H\left ( x_k \right )h\left ( x_k \right )=\bigtriangledown f\left ( x_k \right )$ untuk $h\left ( x_k \right )$.

Step 4 - temukan $x_{k+1}=x_k-h\left ( x_k \right )$.

Step 5- Jika $ \ meninggalkan \ | x_ {k + 1} -x_k \ right \ | <\ varepsilon $ atau$\left \| \bigtriangledown f\left ( x_k \right ) \right \| \leq \varepsilon$ lalu lanjutkan ke langkah 6, setel lagi $k=k+1$ dan lanjutkan ke langkah 2.

Step 6 - Solusi optimal adalah $\hat{x}=x_{k+1}$.

Metode Gradien Konjugasi

Metode ini digunakan untuk memecahkan masalah dari jenis berikut -

$min f\left ( x \right )=\frac{1}{2}x^T Qx-bx$

dimana Q adalah matriks nXn pasti positif dan b konstan.

Diberikan $x_0,\varepsilon,$ menghitung $g_0=Qx_0-b$

Set $d_0=-g_0$ untuk $k=0,1,2,...,$

Set $\alpha_k=\frac{g_{k}^{T}g_k}{d_{k}^{T}Q d_k}$

Menghitung $x_{k+1}=x_k+\alpha_kd_k$

Set $g_{k+1}=g_k+\alpha_kd_k$

Menghitung $\beta_k=\frac{g_{k}^{T}g_k}{d_{k}^{T}Qd_k}$

Menghitung $x_{k+1}=x_k+\alpha_kd_k$

Set $g_{k+1}=x_k+\alpha_kQd_k$

Menghitung $\beta_k=\frac{g_{k+1}^{T}g_{k+1}}{g_{k}^{T}gk}$

Set $d_{k+1}=-g_{k+1}+\beta_kd_k$.