Matematika Diskrit - Teori Grup
Semigroup
Himpunan terbatas atau tak terbatas $ 'S' $ dengan operasi biner $ '\ omicron' $ (Komposisi) disebut semigroup jika ia mengikuti dua kondisi secara bersamaan -
Closure - Untuk setiap pasangan $ (a, b) \ in S, \ :( a \ omicron b) $ harus ada di set $ S $.
Associative - Untuk setiap elemen $ a, b, c \ in S, (a \ omicron b) \ omicron c = a \ omicron (b \ omicron c) $ harus dipegang.
Contoh
Himpunan bilangan bulat positif (tidak termasuk nol) dengan operasi penjumlahan adalah semigroup. Misalnya, $ S = \ lbrace 1, 2, 3, \ dots \ rbrace $
Di sini properti penutupan berlaku untuk setiap pasangan $ (a, b) \ in S, (a + b) $ ada di himpunan S. Misalnya, $ 1 + 2 = 3 \ in S] $
Properti asosiatif juga berlaku untuk setiap elemen $ a, b, c \ di S, (a + b) + c = a + (b + c) $. Misalnya, $ (1 + 2) + 3 = 1 + (2 + 3) = 5 $
Monoid
Monoid adalah semigroup dengan elemen identitas. Elemen identitas (dilambangkan dengan $ e $ atau E) dari himpunan S adalah elemen sedemikian rupa sehingga $ (a \ omicron e) = a $, untuk setiap elemen $ a \ dalam S $. Elemen identitas juga disebut aunit element. Jadi, sebuah monoid memiliki tiga properti secara bersamaan -Closure, Associative, Identity element.
Contoh
Himpunan bilangan bulat positif (tidak termasuk nol) dengan operasi perkalian adalah monoid. $ S = \ lbrace 1, 2, 3, \ dots \ rbrace $
Di sini properti penutupan berlaku untuk setiap pasangan $ (a, b) \ di S, (a \ times b) $ ada di himpunan S. [Misalnya, $ 1 \ times 2 = 2 \ dalam S $ dan seterusnya]
Properti asosiatif juga berlaku untuk setiap elemen $ a, b, c \ in S, (a \ times b) \ times c = a \ times (b \ times c) $ [Misalnya, $ (1 \ times 2) \ times 3 = 1 \ times (2 \ times 3) = 6 $ dan seterusnya]
Properti identitas juga berlaku untuk setiap elemen $ a \ di S, (a \ times e) = a $ [Misalnya, $ (2 \ times 1) = 2, (3 \ times 1) = 3 $ dan seterusnya]. Di sini elemen identitas adalah 1.
Kelompok
Grup adalah monoid dengan elemen terbalik. Elemen invers (dilambangkan dengan I) dari himpunan S adalah elemen sedemikian rupa sehingga $ (a \ omicron I) = (I \ omicron a) = a $, untuk setiap elemen $ a \ dalam S $. Jadi, grup memiliki empat properti secara bersamaan - i) Penutupan, ii) Asosiatif, iii) Elemen identitas, iv) Elemen terbalik. Urutan grup G adalah jumlah elemen di G dan urutan elemen dalam grup adalah bilangan bulat positif terkecil n sehingga an adalah elemen identitas grup G.
Contoh
Himpunan $ N \ times N $ matriks non-singular membentuk grup di bawah operasi perkalian matriks.
Hasil perkalian dua $ N \ times N $ matriks non-singular juga merupakan $ N \ times N $ matriks non-singular yang memegang properti closure.
Perkalian matriks itu sendiri bersifat asosiatif. Karenanya, kepemilikan asosiatif berlaku.
Himpunan $ N \ times N $ matriks non-singular berisi matriks identitas yang memegang properti elemen identitas.
Karena semua matriks adalah non-singular, mereka semua memiliki elemen invers yang juga merupakan matriks nonsingular. Karenanya, properti invers juga berlaku.
Grup Abelian
Grup abelian G adalah grup yang pasangan elemen $ (a, b) \ dalam G $ selalu memegang hukum komutatif. Jadi, sebuah grup memiliki lima properti secara bersamaan - i) Penutupan, ii) Asosiatif, iii) Elemen identitas, iv) Elemen terbalik, v) Komutatif.
Contoh
Himpunan bilangan bulat positif (termasuk nol) dengan operasi penjumlahan adalah grup abelian. $ G = \ lbrace 0, 1, 2, 3, \ dots \ rbrace $
Di sini properti penutupan berlaku untuk setiap pasangan $ (a, b) \ in S, (a + b) $ ada di himpunan S. [Misalnya, $ 1 + 2 = 2 \ dalam S $ dan seterusnya]
Properti asosiatif juga berlaku untuk setiap elemen $ a, b, c \ in S, (a + b) + c = a + (b + c) $ [Misalnya, $ (1 +2) + 3 = 1 + (2 + 3) = 6 $ dan seterusnya]
Properti identitas juga berlaku untuk setiap elemen $ a \ di S, (a \ times e) = a $ [Misalnya, $ (2 \ times 1) = 2, (3 \ times 1) = 3 $ dan seterusnya]. Di sini, elemen identitas adalah 1.
Properti komutatif juga berlaku untuk setiap elemen $ a \ di S, (a \ times b) = (b \ times a) $ [Misalnya, $ (2 \ times 3) = (3 \ times 2) = 3 $ dan seterusnya di]
Grup dan Subkelompok Siklik
SEBUAH cyclic groupadalah grup yang dapat dihasilkan oleh satu elemen. Setiap elemen dari grup siklik adalah kekuatan dari beberapa elemen tertentu yang disebut generator. Grup siklik dapat dihasilkan oleh generator 'g', sehingga setiap elemen grup dapat ditulis sebagai kekuatan generator 'g'.
Contoh
Himpunan bilangan kompleks $ \ lbrace 1, -1, i, -i \ rbrace $ di bawah operasi perkalian adalah grup siklik.
Ada dua generator - $ i $ dan $ –i $ sebagai $ i ^ 1 = i, i ^ 2 = -1, i ^ 3 = -i, i ^ 4 = 1 $ dan juga $ (- i) ^ 1 = -i, (–i) ^ 2 = -1, (–i) ^ 3 = i, (–i) ^ 4 = 1 $ yang mencakup semua elemen grup. Oleh karena itu, ini adalah grup siklik.
Note - A cyclic groupselalu merupakan grup abelian tetapi tidak setiap grup abelian adalah grup siklik. Bilangan rasional yang ditambahkan tidak siklik tetapi abelian.
SEBUAH subgroup H adalah bagian dari grup G (dilambangkan dengan $ H ≤ G $) jika memenuhi empat properti secara bersamaan - Closure, Associative, Identity element, dan Inverse.
Sebuah subgrup H dari grup G yang tidak menyertakan seluruh grup G disebut subgrup yang tepat (Dilambangkan dengan $ H <G $). Sebuah subkelompok dari grup siklik adalah siklik dan subkelompok abelian juga abelian.
Contoh
Misalkan grup $ G = \ lbrace 1, i, -1, -i \ rbrace $
Kemudian beberapa subgrup adalah $ H_1 = \ lbrace 1 \ rbrace, H_2 = \ lbrace 1, -1 \ rbrace $,
Ini bukan subgrup - $ H_3 = \ lbrace 1, i \ rbrace $ karena $ (i) ^ {- 1} = -i $ tidak ada dalam $ H_3 $
Set Pesanan Sebagian (POSET)
Himpunan terurut sebagian terdiri dari himpunan dengan relasi biner yang refleksif, antisimetris, dan transitif. "Kumpulan dipesan sebagian" disingkat POSET.
Contoh
Himpunan bilangan real di bawah operasi biner kurang dari atau sama dengan $ (\ le) $ adalah sebuah poset.
Biarkan set $ S = \ lbrace 1, 2, 3 \ rbrace $ dan operasinya adalah $ \ le $
Relasi akan menjadi $ \ lbrace (1, 1), (2, 2), (3, 3), (1, 2), (1, 3), (2, 3) \ rbrace $
Relasi R ini refleksif sebagai $ \ lbrace (1, 1), (2, 2), (3, 3) \ rbrace \ in R $
Relasi R ini anti simetris, sebagai
$ \ lbrace (1, 2), (1, 3), (2, 3) \ rbrace \ in R \ dan \ \ lbrace (1, 2), (1, 3), (2, 3) \ rbrace ∉ R $
Relasi R ini juga transitif sebagai $ \ lbrace (1,2), (2,3), (1,3) \ rbrace \ in R $.
Oleh karena itu, ini adalah a poset.
Himpunan puncak dari grafik asiklik terarah di bawah 'reachability' operasi adalah sebuah poset.
Diagram Hasse
Diagram Hasse dari sebuah poset adalah graf berarah yang simpulnya merupakan elemen dari poset tersebut dan busurnya menutupi pasangan (x, y) pada poset tersebut. Jika pada poset $ x <y $, maka titik x muncul lebih rendah dari pada titik y pada diagram Hasse. Jika $ x <y <z $ dalam poset, maka panah tidak ditampilkan antara x dan z karena tersirat.
Contoh
Poset dari subset $ \ lbrace 1, 2, 3 \ rbrace = \ lbrace \ emptyset, \ lbrace 1 \ rbrace, \ lbrace 2 \ rbrace, \ lbrace 3 \ rbrace, \ lbrace 1, 2 \ rbrace, \ lbrace 1 , 3 \ rbrace, \ lbrace 2, 3 \ rbrace, \ lbrace 1, 2, 3 \ rbrace \ rbrace $ ditunjukkan oleh diagram Hasse berikut -
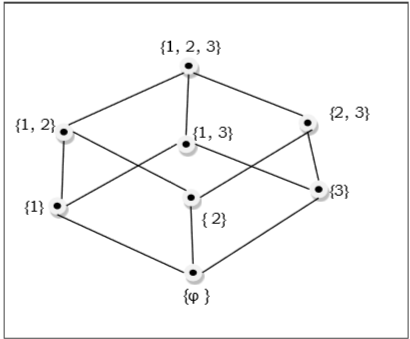
Set Berurutan Linier
Himpunan berurutan linier atau himpunan terurut total adalah himpunan urutan parsial di mana setiap pasangan elemen sebanding. Elemen $ a, b \ dalam S $ dikatakan sebanding jika $ a \ le b $ atau $ b \ le a $ memegang. Hukum trikotomi mendefinisikan himpunan teratur total ini. Himpunan yang benar-benar terurut dapat didefinisikan sebagai kisi distributif yang memiliki properti $ \ lbrace a \ lor b, a \ land b \ rbrace = \ lbrace a, b \ rbrace $ untuk semua nilai a dan b dalam himpunan S.
Contoh
Pangkat dari $ \ lbrace a, b \ rbrace $ yang diurutkan oleh \ subseteq adalah set yang benar-benar terurut karena semua elemen dari set daya $ P = \ lbrace \ emptyset, \ lbrace a \ rbrace, \ lbrace b \ rbrace, \ lbrace a, b \ rbrace \ rbrace $ sebanding.
Contoh kumpulan pesanan non-total
Himpunan $ S = \ lbrace 1, 2, 3, 4, 5, 6 \ rbrace $ dalam operasi x membagi y bukanlah himpunan terurut total.
Di sini, untuk semua $ (x, y) \ dalam S, x | y $ harus ditahan tetapi tidak benar bahwa 2 | 3, karena 2 tidak membagi 3 atau 3 tidak membagi 2. Oleh karena itu, ini bukan himpunan terurut total.
Kisi
Sebuah kisi adalah sebuah poset $ (L, \ le) $ yang setiap pasangan $ \ lbrace a, b \ rbrace \ dalam L $ memiliki batas atas terkecil (dilambangkan dengan $ a \ lor b $) dan batas bawah terbesar ( dilambangkan dengan $ a \ land b $). LUB $ (\ lbrace a, b \ rbrace) $ disebut gabungan dari a dan b. GLB $ (\ lbrace a, b \ rbrace) $ disebut pertemuan a dan b.
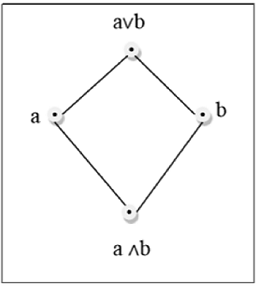
Contoh
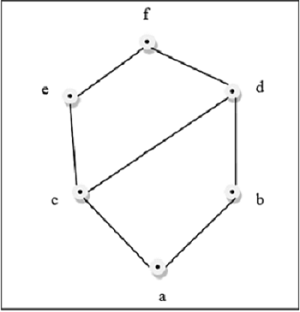
Gambar di atas adalah kisi karena untuk setiap pasangan $ \ lbrace a, b \ rbrace \ dalam L $, ada GLB dan LUB.
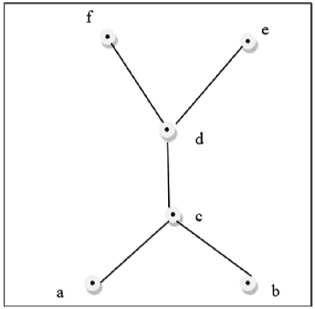
Angka di atas ini bukan kisi karena $ GLB (a, b) $ dan $ LUB (e, f) $ tidak ada.
Beberapa kisi lain dibahas di bawah ini -
Kisi Terikat
Kisi L menjadi kisi terbatas jika memiliki elemen terbesar 1 dan paling sedikit elemen 0.
Kisi Lengkap
Kisi L menjadi kisi komplementer jika kisi tersebut berhingga dan jika setiap elemen dalam kisi memiliki komplemen. Sebuah elemen x memiliki komplemen x 'jika $ \ ada x (x \ tanah x' = 0 dan x \ lor x '= 1) $
Kisi Distributif
Jika kisi memenuhi dua properti distribusi berikut, ini disebut kisi distributif.
$ a \ lor (b \ land c) = (a \ lor b) \ land (a \ lor c) $
$ a \ tanah (b \ lor c) = (a \ tanah b) \ lor (a \ tanah c) $
Kisi Modular
Jika kisi memenuhi properti berikut, ini disebut kisi modular.
$ a \ tanah (b \ lor (a \ tanah d)) = (a \ tanah b) \ lor (a \ tanah d) $
Properti Kisi
Properti Idempoten
$ a \ lor a = a $
$ a \ land a = a $
Properti Penyerapan
$ a \ lor (a \ land b) = a $
$ a \ tanah (a \ lor b) = a $
Properti Komutatif
$ a \ lor b = b \ lor a $
$ a \ land b = b \ land a $
Properti Asosiatif
$ a \ lor (b \ lor c) = (a \ lor b) \ lor c $
$ a \ land (b \ land c) = (a \ land b) \ land c $
Dual of a Lattice
Kisi ganda diperoleh dengan menukar operasi '$ \ lor $' dan '$ \ land $'.
Contoh
Ganda dari $ \ lbrack a \ lor (b \ land c) \ rbrack \ adalah \ \ lbrack a \ land (b \ lor c) \ rbrack $