Matematika Diskrit - Merentang Pohon
Pohon rentang dari grafik tidak berarah yang terhubung $ G $ adalah pohon yang minimal mencakup semua simpul $ G $. Sebuah grafik mungkin memiliki banyak pohon merentang.
Contoh
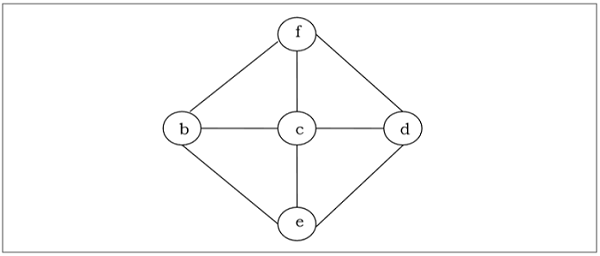
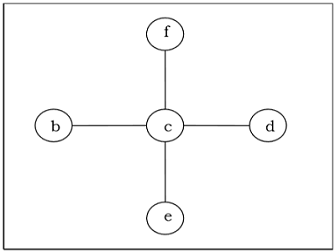
Pohon Rentang Minimum
Pohon bentang dengan bobot yang ditetapkan kurang dari atau sama dengan bobot setiap pohon bentang yang mungkin dari graf berbobot, terhubung dan tidak berarah $ G $, disebut pohon rentang minimum (MST). Bobot pohon bentang adalah jumlah dari semua bobot yang ditetapkan ke setiap tepi pohon bentang.
Contoh
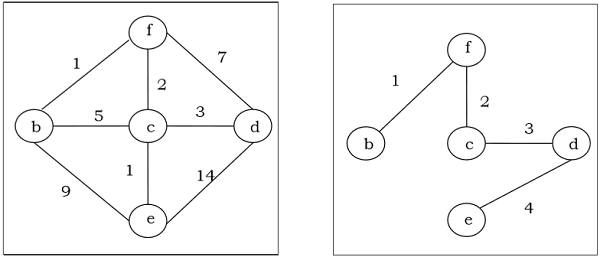
Algoritma Kruskal
Algoritma Kruskal adalah algoritma rakus yang menemukan pohon rentang minimum untuk grafik berbobot yang terhubung. Ia menemukan pohon dari grafik yang mencakup setiap simpul dan berat total dari semua tepi di pohon kurang dari atau sama dengan setiap pohon rentang yang mungkin.
Algoritma
Step 1 - Susun semua tepi grafik $ G (V, E) $ dalam urutan menaik sesuai bobot tepinya.
Step 2 - Pilih tepi berbobot terkecil dari grafik dan periksa apakah itu membentuk siklus dengan pohon rentang yang terbentuk sejauh ini.
Step 3 - Jika tidak ada siklus, sertakan tepi ini ke pohon rentang, jika tidak, buang.
Step 4 - Ulangi Langkah 2 dan Langkah 3 hingga $ (V-1) $ jumlah tepi yang tersisa di pohon rentang.
Problem
Misalkan kita ingin mencari pohon rentang minimum untuk graf G berikut menggunakan algoritma Kruskal.
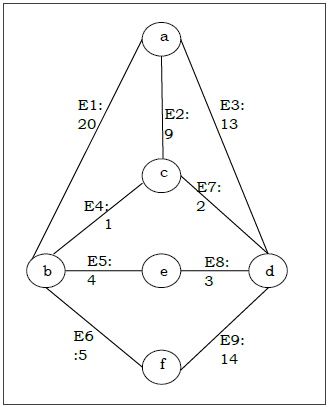
Solution
Dari grafik di atas kami membuat tabel berikut -
| Tepi No. | Pasangan Vertex | Bobot Tepi |
|---|---|---|
| E1 | (a, b) | 20 |
| E2 | (a, c) | 9 |
| E3 | (a, d) | 13 |
| E4 | (b, c) | 1 |
| E5 | (b, e) | 4 |
| E6 | (b, f) | 5 |
| E7 | (c, d) | 2 |
| E8 | (d, e) | 3 |
| E9 | (d, f) | 14 |
Sekarang kita akan mengatur ulang tabel dalam urutan menaik sehubungan dengan bobot Edge -
| Tepi No. | Pasangan Vertex | Bobot Tepi |
|---|---|---|
| E4 | (b, c) | 1 |
| E7 | (c, d) | 2 |
| E8 | (d, e) | 3 |
| E5 | (b, e) | 4 |
| E6 | (b, f) | 5 |
| E2 | (a, c) | 9 |
| E3 | (a, d) | 13 |
| E9 | (d, f) | 14 |
| E1 | (a, b) | 20 |
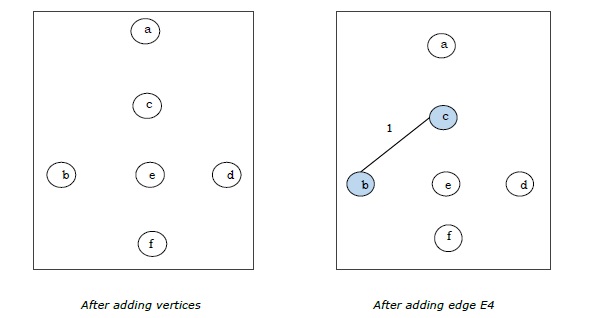
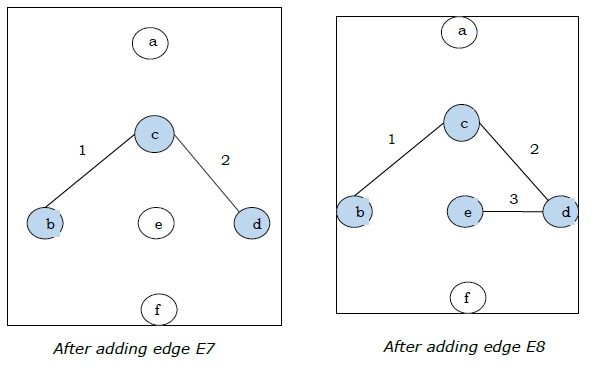
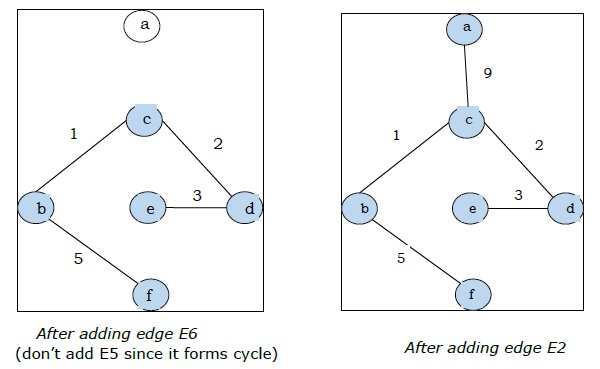
Karena kita mendapatkan semua 5 sisi pada gambar terakhir, kita menghentikan algoritme dan ini adalah pohon rentang minimal dan bobot totalnya adalah $ (1 + 2 + 3 + 5 + 9) = 20 $.
Algoritma Prim
Algoritme Prim, ditemukan pada tahun 1930 oleh ahli matematika, Vojtech Jarnik dan Robert C. Prim, adalah algoritme serakah yang menemukan pohon rentang minimum untuk grafik berbobot yang terhubung. Ia menemukan pohon dari grafik yang mencakup setiap simpul dan berat total dari semua tepi di pohon kurang dari atau sama dengan setiap pohon rentang yang mungkin. Algoritme Prim lebih cepat pada grafik yang padat.
Algoritma
Inisialisasi pohon rentang minimal dengan satu simpul, dipilih secara acak dari grafik.
Ulangi langkah 3 dan 4 hingga semua simpul dimasukkan ke dalam pohon.
Pilih tepi yang menghubungkan pohon dengan simpul yang belum ada di pohon, sehingga bobot tepi minimal dan masuknya tepi tidak membentuk siklus.
Tambahkan tepi yang dipilih dan simpul yang terhubung ke pohon.
Problem
Misalkan kita ingin mencari pohon rentang minimum untuk grafik G berikut menggunakan algoritma Prim.
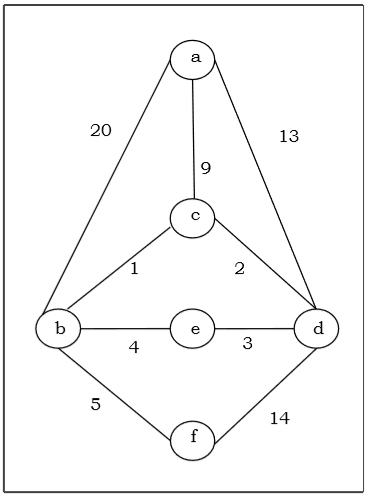
Solution
Di sini kita mulai dengan simpul 'a' dan melanjutkan.
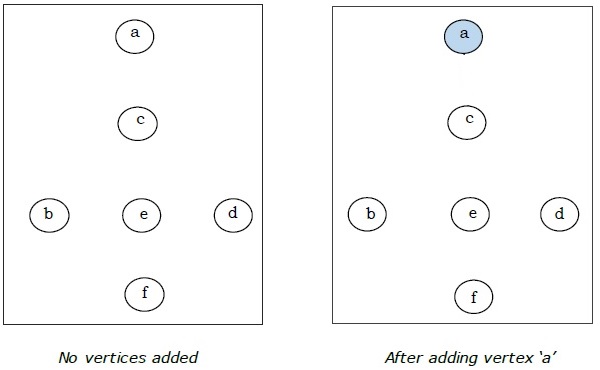
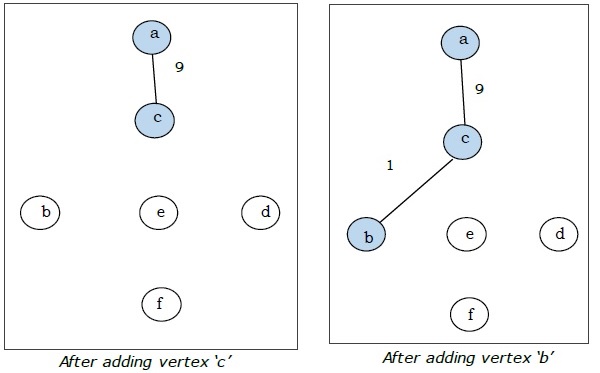
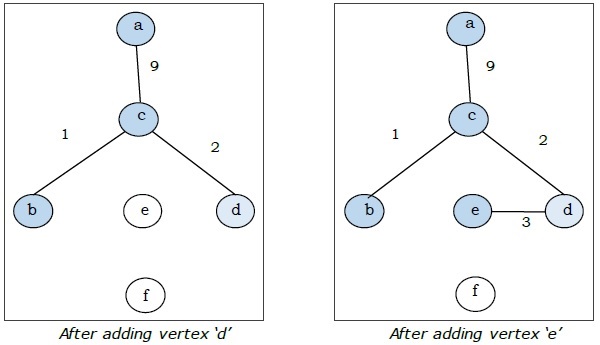
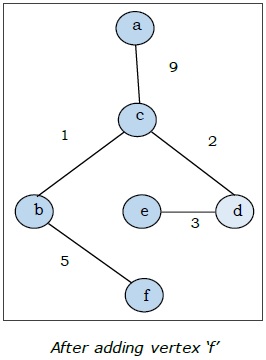
Ini adalah pohon rentang minimal dan berat totalnya adalah $ (1 + 2 + 3 + 5 + 9) = 20 $.