Penyederhanaan Fungsi Boolean

Penyederhanaan Menggunakan Fungsi Aljabar

Dalam pendekatan ini, satu ekspresi Boolean diminimalkan menjadi ekspresi yang setara dengan menerapkan identitas Boolean.

Masalah 1

Minimalkan ekspresi Boolean berikut menggunakan identitas Boolean -

$$ F (A, B, C) = A'B + BC '+ BC + AB'C' $$

Larutan

Diketahui, $ F (A, B, C) = A'B + BC '+ BC + AB'C' $

Atau, $ F (A, B, C) = A'B + (BC '+ BC') + BC + AB'C '$

[Menurut hukum idempoten, BC '= BC' + BC ']

Atau, $ F (A, B, C) = A'B + (BC '+ BC) + (BC' + AB'C ') $

Atau, $ F (A, B, C) = A'B + B (C '+ C) + C' (B + AB ') $

[Dengan hukum distributif]

Atau, $ F (A, B, C) = A'B + B.1 + C '(B + A) $

[(C '+ C) = 1 dan hukum absorpsi (B + AB') = (B + A)]

Atau, $ F (A, B, C) = A'B + B + C '(B + A) $

[B.1 = B]

Atau, $ F (A, B, C) = B (A '+ 1) + C' (B + A) $

Atau, $ F (A, B, C) = B.1 + C '(B + A) $

[(A '+ 1) = 1]

Atau, $ F (A, B, C) = B + C '(B + A) $

[Sebagai, B.1 = B]

Atau, $ F (A, B, C) = B + BC '+ AC' $

Atau, $ F (A, B, C) = B (1 + C ') + AC' $

Atau, $ F (A, B, C) = B.1 + AC '$

[Sebagai, (1 + C ') = 1]

Atau, $ F (A, B, C) = B + AC '$

[Sebagai, B.1 = B]

Jadi, $ F (A, B, C) = B + AC '$ adalah bentuk yang diminimalkan.

Masalah 2

Minimalkan ekspresi Boolean berikut menggunakan identitas Boolean -

$$ F (A, B, C) = (A + B) (A + C) $$

Larutan

Diketahui, $ F (A, B, C) = (A + B) (A + C) $

Atau, $ F (A, B, C) = AA + AC + BA + BC $ [Menerapkan Aturan distributif]

Atau, $ F (A, B, C) = A + AC + BA + BC $ [Menerapkan Hukum Idempoten]

Atau, $ F (A, B, C) = A (1 + C) + BA + BC $ [Menerapkan Hukum distributif]

Atau, $ F (A, B, C) = A + BA + BC $ [Menerapkan Hukum dominasi]

Atau, $ F (A, B, C) = (A + 1). A + BC $ [Menerapkan Hukum distributif]

Atau, $ F (A, B, C) = 1.A + BC $ [Menerapkan Hukum dominasi]

Atau, $ F (A, B, C) = A + BC $ [Menerapkan Hukum dominasi]

Jadi, $ F (A, B, C) = A + BC $ adalah bentuk yang diminimalkan.

Peta Karnaugh

Peta Karnaugh (K-map), diperkenalkan oleh Maurice Karnaughin pada tahun 1953, adalah representasi tabel kebenaran seperti kisi yang digunakan untuk menyederhanakan ekspresi aljabar boolean. Peta Karnaugh memiliki nol dan satu entri di posisi yang berbeda. Ini menyediakan pengelompokan bersama ekspresi Boolean dengan faktor umum dan menghilangkan variabel yang tidak diinginkan dari ekspresi. Dalam K-map, melintasi batas sel vertikal atau horizontal selalu merupakan perubahan hanya satu variabel.

Contoh 1

Tabel kebenaran arbitrer diambil di bawah ini -

SEBUAH	B	A operasi B
0	0	w
0	1	x
1	0	y
1	1	z

Sekarang kita akan membuat k-map untuk tabel kebenaran di atas -

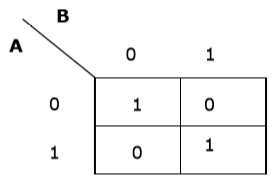
Contoh 2

Sekarang kita akan membuat K-map untuk ekspresi - AB + A'B '

Penyederhanaan Menggunakan K-map

K-map menggunakan beberapa aturan untuk penyederhanaan ekspresi Boolean dengan menggabungkan bersama sel yang berdekatan menjadi satu suku. Aturannya dijelaskan di bawah -

Rule 1 - Sel apa pun yang mengandung nol tidak dapat dikelompokkan.

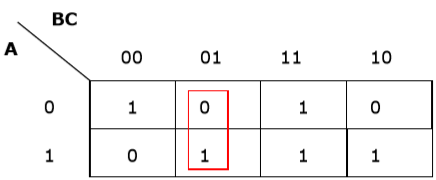
Pengelompokan salah

Rule 2 - Grup harus berisi 2n sel (n mulai dari 1).

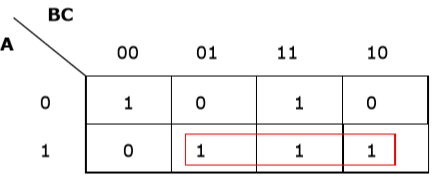
Pengelompokan salah

Rule 3 - Pengelompokan harus horizontal atau vertikal, tetapi tidak boleh diagonal.

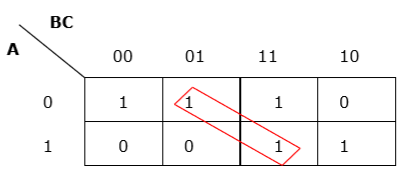
Pengelompokan diagonal salah

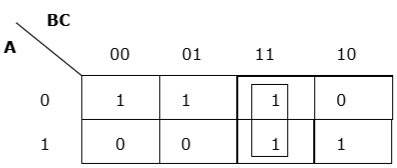
Pengelompokan vertikal yang tepat

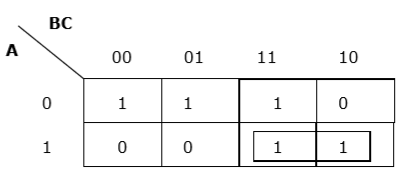
Pengelompokan horizontal yang tepat

Rule 4 - Grup harus dicakup seluas mungkin.

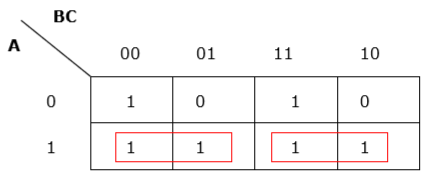
Pengelompokan tidak memadai

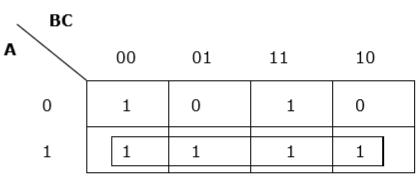
Pengelompokan yang tepat

Rule 5 - Jika 1 dari sel mana pun tidak dapat dikelompokkan dengan sel lain, itu akan bertindak sebagai grup itu sendiri.

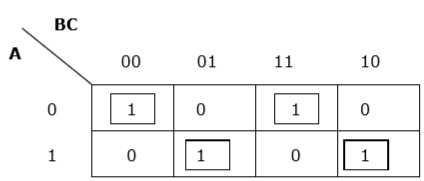
Pengelompokan yang tepat

Rule 6 - Grup mungkin tumpang tindih tetapi harus ada grup sesedikit mungkin.

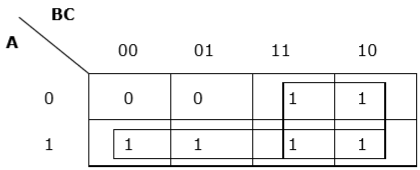
Pengelompokan yang tepat

Rule 7 - Sel / sel paling kiri dapat dikelompokkan dengan sel / sel paling kanan dan sel / sel paling atas dapat dikelompokkan dengan sel / sel paling bawah.

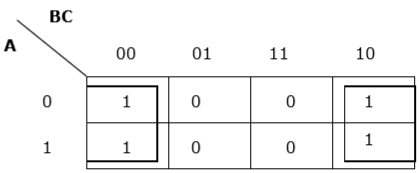
Pengelompokan yang tepat

Masalah

Minimalkan ekspresi Boolean berikut menggunakan K-map -

$$ F (A, B, C) = A'BC + A'BC '+ AB'C' + AB'C $$

Larutan

Setiap istilah dimasukkan ke dalam k-map dan kami mendapatkan yang berikut -

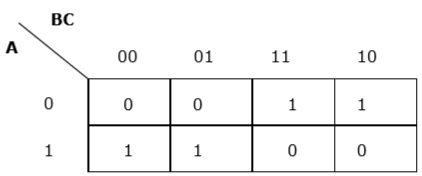
K-map untuk F (A, B, C)

Sekarang kita akan mengelompokkan sel 1 sesuai dengan aturan yang disebutkan di atas -

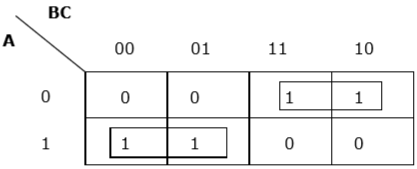
K-map untuk F (A, B, C)

Kami memiliki dua kelompok yang disebut sebagai $ A'B $ dan $ AB '$. Karenanya, $ F (A, B, C) = A'B + AB '= A \ oplus B $. Ini adalah bentuk yang diminimalkan.