Model Grafik & Grafik
Bagian sebelumnya mengemukakan berbagai alat untuk penalaran, pemeriksaan, dan pemecahan masalah. Pada bagian ini, kita akan mempelajari struktur diskrit yang menjadi dasar perumusan banyak masalah kehidupan nyata.
Dua struktur terpisah yang akan kita bahas adalah grafik dan pohon. Grafik adalah sekumpulan titik yang disebut simpul atau simpul, yang saling berhubungan oleh sekumpulan garis yang disebut tepi. Studi tentang grafik, ataugraph theory adalah bagian penting dari sejumlah disiplin ilmu di bidang matematika, teknik, dan ilmu komputer.
Apa itu Grafik?
Definition - Sebuah grafik (dilambangkan sebagai $ G = (V, E) $) terdiri dari satu set simpul atau node V yang tidak kosong dan satu set tepi E.
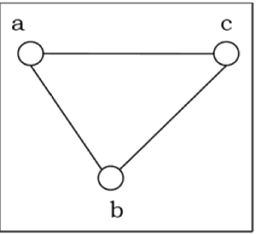
Example - Mari kita pertimbangkan, sebuah Grafik adalah $ G = (V, E) $ di mana $ V = \ lbrace a, b, c, d \ rbrace $ dan $ E = \ lbrace \ lbrace a, b \ rbrace, \ lbrace a , c \ rbrace, \ lbrace b, c \ rbrace, \ lbrace c, d \ rbrace \ rbrace $

Degree of a Vertex - Derajat simpul V dari graf G (dilambangkan dengan derajat (V)) adalah banyaknya sisi yang bersisian dengan simpul V.
| Puncak | Gelar | Bahkan aneh |
|---|---|---|
| Sebuah | 2 | bahkan |
| b | 2 | bahkan |
| c | 3 | aneh |
| d | 1 | aneh |
Even and Odd Vertex - Jika derajat dari simpul genap, simpul tersebut disebut simpul genap dan jika derajat dari simpul ganjil, simpul itu disebut simpul ganjil.
Degree of a Graph- Derajat suatu graf adalah derajat simpul terbesar dari graf tersebut. Untuk grafik di atas derajat grafiknya adalah 3.
The Handshaking Lemma - Dalam grafik, jumlah semua derajat dari semua simpul sama dengan dua kali jumlah sisi.
Jenis Grafik
Ada berbagai jenis grafik, yang akan kita pelajari di bagian berikut.
Grafik Null
Grafik nol tidak memiliki tepi. Grafik nol dari $ n $ simpul dilambangkan dengan $ N_n $

Grafik Sederhana
Grafik disebut grafik sederhana / grafik ketat jika grafik tidak berarah dan tidak mengandung loop atau banyak sisi.

Multi-Grafik
Jika dalam sebuah graf beberapa sisi di antara kumpulan simpul yang sama diperbolehkan, ini disebut Multigraf. Dengan kata lain, ini adalah grafik yang memiliki setidaknya satu loop atau beberapa sisi.

Grafik Berarah dan Tidak Terarah
Graf $ G = (V, E) $ disebut graf berarah jika himpunan tepi terbuat dari pasangan simpul berurutan dan graf disebut tak berarah jika himpunan tepi terbuat dari pasangan simpul tak beraturan.


Grafik Terhubung dan Terputus
Grafik dihubungkan jika ada dua simpul pada grafik yang dihubungkan oleh sebuah jalur; sedangkan grafik terputus jika setidaknya dua simpul dari grafik tidak terhubung oleh jalur. Jika grafik G terputus, maka setiap sub-grafik terhubung maksimal dari $ G $ disebut komponen terhubung dari grafik $ G $.


Grafik Reguler
Suatu graf beraturan jika semua simpul pada graf tersebut memiliki derajat yang sama. Dalam graf biasa G dengan derajat $ r $, derajat setiap simpul $ G $ adalah r.

Grafik Lengkap
Grafik disebut graf lengkap jika setiap dua pasangan simpul dihubungkan oleh tepat satu sisi. Grafik lengkap dengan n simpul dilambangkan dengan $ K_n $
Grafik Siklus
Grafik yang terdiri dari satu siklus disebut grafik siklus. Grafik siklus dengan n simpul dilambangkan dengan $ C_n $

Graf Bipartit
Jika himpunan puncak dari sebuah graf G dapat dipecah menjadi dua himpunan yang saling lepas, $ V_1 $ dan $ V_2 $, sedemikian rupa sehingga setiap sisi dalam graf tersebut bergabung dengan simpul di $ V_1 $ menjadi simpul di $ V_2 $, dan tidak ada sisi pada G yang menghubungkan dua simpul pada $ V_1 $ atau dua simpul pada $ V_2 $, maka graf $ G $ disebut graf bipartit.

Graf Bipartit Lengkap
Graf bipartit lengkap adalah graf bipartit di mana setiap simpul pada himpunan pertama digabungkan ke setiap simpul tunggal pada himpunan kedua. Grafik bipartit lengkap dilambangkan dengan $ K_ {x, y} $ dimana grafik $ G $ berisi $ x $ simpul pada set pertama dan $ y $ simpul pada set kedua.

Representasi Grafik
Ada dua cara utama untuk merepresentasikan grafik -
- Matriks Adjacency
- Daftar Adjacency
Matriks Adjacency
Matriks Adjacency $ A [V] [V] $ adalah larik 2D berukuran $ V \ dikali V $ di mana $ V $ adalah jumlah simpul dalam graf tak berarah. Jika ada tepi antara $ V_x $ hingga $ V_y $ maka nilai $ A [V_x] [V_y] = 1 $ dan $ A [V_y] [V_x] = 1 $, jika tidak, nilainya akan nol. Dan untuk graf berarah, jika ada sisi antara $ V_x $ hingga $ V_y $, maka nilai $ A [V_x] [V_y] = 1 $, jika tidak nilainya akan nol.
Adjacency Matrix of an Undirected Graph
Mari kita pertimbangkan grafik tidak berarah berikut dan buat matriks ketetanggaan -

Matriks kedekatan dari grafik tidak berarah di atas akan menjadi -
a |
b |
c |
d |
|
a |
0 |
1 |
1 |
0 |
b |
1 |
0 |
1 |
0 |
c |
1 |
1 |
0 |
1 |
d |
0 |
0 |
1 |
0 |
Adjacency Matrix of a Directed Graph
Mari kita pertimbangkan grafik berarah berikut dan membangun matriks ketetanggaannya -

Matriks kedekatan dari grafik berarah di atas akan menjadi -
a |
b |
c |
d |
|
a |
0 |
1 |
1 |
0 |
b |
0 |
0 |
1 |
0 |
c |
0 |
0 |
0 |
1 |
d |
0 |
0 |
0 |
0 |
Daftar Adjacency
Dalam daftar berdampingan, larik $ (A [V]) $ daftar tertaut digunakan untuk mewakili grafik G dengan $ V $ jumlah simpul. Entri $ A [V_x] $ mewakili daftar terkait dari simpul yang berdekatan dengan simpul $ Vx-th $. Daftar kedekatan dari grafik tidak berarah seperti yang ditunjukkan pada gambar di bawah ini -

Grafik planar vs. non-planar
Planar graph- Grafik $ G $ disebut grafik planar jika dapat digambar dalam bidang tanpa ada sisi yang bersilangan. Jika kita menggambar grafik pada bidang tanpa perpotongan tepi disebut embedding grafik pada bidang tersebut.

Non-planar graph - Grafik non-planar jika tidak dapat digambar pada bidang yang tidak memotong tepi grafik.

Isomorfisme
Jika dua graf G dan H berisi jumlah simpul yang sama yang dihubungkan dengan cara yang sama, keduanya disebut graf isomorfik (dilambangkan dengan $ G \ cong H $).
Lebih mudah untuk memeriksa non-isomorfisme daripada isomorfisme. Jika salah satu dari kondisi berikut ini terjadi, maka dua grafik non-isomorfik -
- Jumlah komponen yang terhubung berbeda
- Kardinalitas himpunan vertex berbeda
- Kardinalitas himpunan tepi berbeda
- Urutan derajat berbeda
Contoh
Grafik berikut bersifat isomorfik -
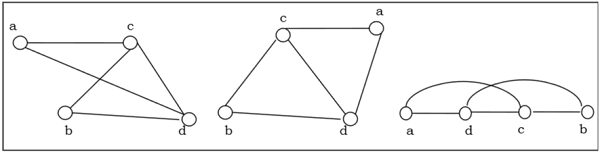
Homomorfisme
Homomorfisme dari grafik $ G $ ke grafik $ H $ adalah pemetaan (Mungkin bukan pemetaan bijective) $ h: G \ rightarrow H $ sedemikian rupa sehingga - $ (x, y) \ in E (G) \ rightarrow (h (x), h (y)) \ dalam E (H) $. Ini memetakan simpul yang berdekatan dari grafik $ G $ ke simpul yang berdekatan dari grafik $ H $.
Sifat Homomorfisme
Homomorfisme adalah isomorfisme jika merupakan pemetaan bijective.
Homomorfisme selalu mempertahankan tepi dan keterhubungan suatu grafik.
Komposisi homomorfisme juga homomorfisme.
Untuk mengetahui apakah terdapat graf homomorfik dari graf lain adalah soal NP lengkap.
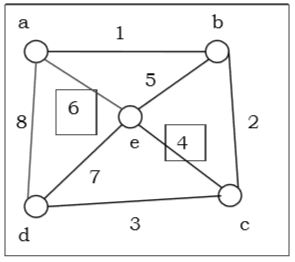
Grafik Euler
Grafik terhubung $ G $ disebut grafik Euler, jika ada jalur tertutup yang mencakup setiap tepi grafik $ G $. Jalur Euler adalah jalur yang menggunakan setiap tepi grafik tepat satu kali. Jalur Euler dimulai dan diakhiri pada simpul yang berbeda.
Sirkuit Euler adalah sirkuit yang menggunakan setiap tepi grafik tepat satu kali. Sirkuit Euler selalu dimulai dan diakhiri pada titik yang sama. Grafik terhubung $ G $ adalah grafik Euler jika dan hanya jika semua simpul dari $ G $ memiliki derajat genap, dan grafik terhubung $ G $ adalah Eulerian jika dan hanya jika himpunan tepinya dapat didekomposisi menjadi siklus.

Grafik di atas adalah grafik Euler sebagai $ “a \: 1 \: b \: 2 \: c \: 3 \: d \: 4 \: e \: 5 \: c \: 6 \: f \: 7 \: g ”$ menutupi semua tepi grafik.

Grafik Hamiltonian
Graf yang terhubung $ G $ disebut graf Hamilton jika ada siklus yang mencakup setiap simpul $ G $ dan siklus tersebut disebut siklus Hamiltonian. Jalan Hamilton dalam grafik $ G $ adalah jalan yang melewati setiap simpul tepat satu kali.
Jika $ G $ adalah grafik sederhana dengan n simpul, di mana $ n \ geq 3 $ Jika $ deg (v) \ geq \ frac {n} {2} $ untuk setiap simpul $ v $, maka grafik $ G $ adalah Grafik Hamiltonian. Ini disebutDirac's Theorem.
Jika $ G $ adalah grafik sederhana dengan $ n $ simpul, di mana $ n \ geq 2 $ if $ deg (x) + deg (y) \ geq n $ untuk setiap pasang simpul yang tidak berdekatan x dan y, maka grafik $ G $ adalah grafik Hamiltonian. Ini disebutOre's theorem.