Matematika Diskrit - Himpunan
Ahli matematika Jerman G. Cantormemperkenalkan konsep set. Dia telah mendefinisikan himpunan sebagai kumpulan objek yang pasti dan dapat dibedakan yang dipilih melalui aturan atau deskripsi tertentu.
SetTeori membentuk dasar dari beberapa bidang studi lain seperti teori penghitungan, hubungan, teori grafik dan mesin keadaan hingga. Dalam bab ini, kami akan membahas berbagai aspekSet Theory.
Set - Definisi
Satu set adalah kumpulan elemen berbeda yang tidak berurutan. Sebuah himpunan dapat ditulis secara eksplisit dengan mendaftar elemen-elemennya menggunakan set braket. Jika urutan elemen diubah atau elemen apa pun dari himpunan diulang, itu tidak membuat perubahan apa pun dalam himpunan.
Beberapa Contoh Set
- Satu set semua bilangan bulat positif
- Satu set dari semua planet di tata surya
- Satu set semua negara bagian di India
- Satu set semua huruf kecil alfabet
Representasi dari sebuah Himpunan
Set dapat diwakili dalam dua cara -
- Daftar atau Bentuk Tabular
- Atur Notasi Pembangun
Daftar atau Bentuk Tabular
Himpunan diwakili dengan mendaftar semua elemen yang menyusunnya. Elemen-elemen tersebut diapit dengan tanda kurung dan dipisahkan dengan koma.
Example 1 - Kumpulan huruf vokal dalam alfabet Inggris, $ A = \ lbrace a, e, i, o, u \ rbrace $
Example 2 - Kumpulan bilangan ganjil kurang dari 10, $ B = \ lbrace 1,3,5,7,9 \ rbrace $
Atur Notasi Pembangun
Himpunan didefinisikan dengan menentukan properti yang memiliki kesamaan dengan elemen-elemen himpunan. Set tersebut dideskripsikan sebagai $ A = \ lbrace x: p (x) \ rbrace $
Example 1 - Set $ \ lbrace a, e, i, o, u \ rbrace $ ditulis sebagai -
$ A = \ lbrace x: \ text {x adalah vokal dalam alfabet Inggris} \ rbrace $
Example 2 - Set $ \ lbrace 1,3,5,7,9 \ rbrace $ ditulis sebagai -
$ B = \ lbrace x: 1 \ le x \ lt 10 \ dan \ (x \% 2) \ ne 0 \ rbrace $
Jika sebuah elemen x adalah anggota dari himpunan S apapun, itu dilambangkan dengan $ x \ dalam S $ dan jika sebuah elemen y bukan anggota dari himpunan S, itu dilambangkan dengan $ y \ notin S $.
Example- Jika $ S = \ lbrace1, 1.2, 1.7, 2 \ rbrace, 1 \ in S $ tapi $ 1.5 \ notin S $
Beberapa Set Penting
N - himpunan semua bilangan asli = $ \ lbrace1, 2, 3, 4, ..... \ rbrace $
Z - himpunan semua bilangan bulat = $ \ lbrace ....., -3, -2, -1, 0, 1, 2, 3, ..... \ rbrace $
Z+ - himpunan semua bilangan bulat positif
Q - himpunan semua bilangan rasional
R - himpunan semua bilangan real
W - himpunan semua bilangan bulat
Kardinalitas Set
Kardinalitas dari himpunan S, dilambangkan dengan $ | S | $, adalah banyaknya elemen dari himpunan tersebut. Nomor tersebut juga disebut sebagai nomor pokok. Jika suatu himpunan memiliki jumlah elemen yang tak terbatas, kardinalitasnya adalah $ \ infty $.
Example- $ | \ lbrace 1, 4, 3, 5 \ rbrace | = 4, | \ lbrace 1, 2, 3, 4, 5, \ dots \ rbrace | = \ banyak $
Jika ada dua himpunan X dan Y,
$ | X | = | Y | $ menunjukkan dua himpunan X dan Y yang memiliki kardinalitas yang sama. Ini terjadi ketika jumlah elemen di X sama persis dengan jumlah elemen di Y. Dalam kasus ini, terdapat fungsi bijektiva 'f' dari X ke Y.
$ | X | \ le | Y | $ menunjukkan bahwa himpunan X kardinalitas kurang dari atau sama dengan himpunan kardinalitas Y. Ini terjadi ketika jumlah elemen di X kurang dari atau sama dengan Y. Di sini, terdapat fungsi injeksi 'f' dari X ke Y.
$ | X | \ lt | Y | $ menunjukkan bahwa himpunan X lebih kecil dari himpunan kardinalitas Y. Ini terjadi ketika jumlah elemen di X lebih kecil dari pada Y. Di sini, fungsi 'f' dari X ke Y adalah fungsi injektif tetapi tidak bijektiva.
$ Jika \ | X | \ le | Y | $ dan $ | X | \ ge | Y | $ lalu $ | X | = | Y | $. Himpunan X dan Y biasanya disebut sebagai himpunan ekivalen.
Jenis Set
Set dapat diklasifikasikan ke dalam banyak jenis. Beberapa diantaranya adalah finite, infinite, subset, universal, proper, singleton set, dll.
Set Hingga
Himpunan yang berisi sejumlah elemen tertentu disebut himpunan hingga.
Example- $ S = \ lbrace x \: | \: x \ dalam N $ dan $ 70 \ gt x \ gt 50 \ rbrace $
Set Tak Terbatas
Himpunan yang berisi elemen dalam jumlah tak hingga disebut himpunan tak hingga.
Example- $ S = \ lbrace x \: | \: x \ dalam N $ dan $ x \ gt 10 \ rbrace $
Subset
Himpunan X adalah himpunan bagian dari himpunan Y (Ditulis sebagai $ X \ subseteq Y $) jika setiap elemen X adalah elemen dari himpunan Y.
Example 1- Misalkan, $ X = \ lbrace 1, 2, 3, 4, 5, 6 \ rbrace $ dan $ Y = \ lbrace 1, 2 \ rbrace $. Di sini himpunan Y adalah himpunan bagian dari himpunan X karena semua elemen himpunan Y ada dalam himpunan X. Oleh karena itu, kita dapat menulis $ Y \ subseteq X $.
Example 2- Misalkan, $ X = \ lbrace 1, 2, 3 \ rbrace $ dan $ Y = \ lbrace 1, 2, 3 \ rbrace $. Di sini himpunan Y adalah himpunan bagian (Bukan himpunan bagian yang sesuai) dari himpunan X karena semua elemen himpunan Y ada di himpunan X. Oleh karena itu, kita dapat menulis $ Y \ subseteq X $.
Bagian yang tepat
Istilah "subset yang tepat" dapat didefinisikan sebagai "subset dari tetapi tidak sama dengan". Himpunan X adalah himpunan bagian yang tepat dari himpunan Y (Ditulis sebagai $ X \ subset Y $) jika setiap elemen X adalah elemen dari himpunan Y dan $ | X | \ lt | Y | $.
Example- Misalkan, $ X = \ lbrace 1, 2, 3, 4, 5, 6 \ rbrace $ dan $ Y = \ lbrace 1, 2 \ rbrace $. Di sini set $ Y \ subset X $ karena semua elemen dalam $ Y $ juga terdapat dalam $ X $ dan $ X $ memiliki setidaknya satu elemen lebih dari yang ditetapkan $ Y $.
Set Universal
Ini adalah kumpulan semua elemen dalam konteks atau aplikasi tertentu. Semua himpunan dalam konteks atau aplikasi itu pada dasarnya adalah himpunan bagian dari himpunan universal ini. Set universal direpresentasikan sebagai $ U $.
Example- Kami dapat mendefinisikan $ U $ sebagai himpunan semua hewan di bumi. Dalam hal ini, kumpulan semua mamalia adalah bagian dari $ U $, kumpulan semua ikan adalah bagian dari $ U $, kumpulan semua serangga adalah bagian dari $ U $, dan seterusnya.
Set Kosong atau Set Null
Satu set kosong tidak berisi elemen. Ini dilambangkan dengan $ \ emptyset $. Karena jumlah elemen dalam himpunan kosong terbatas, himpunan kosong adalah himpunan berhingga. Kardinalitas himpunan kosong atau himpunan nol adalah nol.
Example- $ S = \ lbrace x \: | \: x \ dalam N $ dan $ 7 \ lt x \ lt 8 \ rbrace = \ emptyset $
Singleton Set atau Satuan Set
Singleton set atau unit set hanya berisi satu elemen. Satu set tunggal dilambangkan dengan $ \ lbrace s \ rbrace $.
Example- $ S = \ lbrace x \: | \: x \ in N, \ 7 \ lt x \ lt 9 \ rbrace $ = $ \ lbrace 8 \ rbrace $
Set yang Sama
Jika dua himpunan berisi elemen yang sama, keduanya dikatakan sama.
Example - Jika $ A = \ lbrace 1, 2, 6 \ rbrace $ dan $ B = \ lbrace 6, 1, 2 \ rbrace $, mereka sama karena setiap elemen dari set A adalah elemen dari set B dan setiap elemen dari set B adalah elemen dari himpunan A.
Set Setara
Jika kardinalitas dari dua himpunan adalah sama, disebut himpunan ekuivalen.
Example- Jika $ A = \ lbrace 1, 2, 6 \ rbrace $ dan $ B = \ lbrace 16, 17, 22 \ rbrace $, keduanya setara karena kardinalitas A sama dengan kardinalitas B. yaitu $ | A | = | B | = 3 $
Set Tumpang Tindih
Dua set yang memiliki setidaknya satu elemen umum disebut set tumpang tindih.
Jika set tumpang tindih -
$ n (A \ cangkir B) = n (A) + n (B) - n (A \ cap B) $
$ n (A \ cangkir B) = n (A - B) + n (B - A) + n (A \ cap B) $
$ n (A) = n (A - B) + n (A \ cap B) $
$ n (B) = n (B - A) + n (A \ cap B) $
Example- Misalkan, $ A = \ lbrace 1, 2, 6 \ rbrace $ dan $ B = \ lbrace 6, 12, 42 \ rbrace $. Ada elemen umum '6', maka set ini adalah set yang tumpang tindih.
Set Disjoint
Dua himpunan A dan B disebut himpunan terpisah jika tidak memiliki satu elemen pun yang sama. Oleh karena itu, set pemutusan hubungan kerja memiliki properti berikut -
$ n (A \ cap B) = \ blankset $
$ n (A \ cangkir B) = n (A) + n (B) $
Example - Misalkan, $ A = \ lbrace 1, 2, 6 \ rbrace $ dan $ B = \ lbrace 7, 9, 14 \ rbrace $, tidak ada satu pun elemen yang sama, maka set ini adalah set yang tumpang tindih.
Diagram Venn
Diagram Venn, ditemukan pada tahun 1880 oleh John Venn, adalah diagram skematik yang menunjukkan semua kemungkinan hubungan logis antara himpunan matematika yang berbeda.
Examples
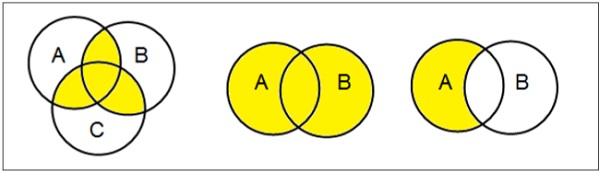
Atur Operasi
Operasi Set termasuk Set Union, Set Intersection, Set Difference, Complement of Set, dan Cartesian Product.
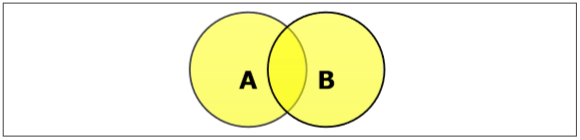
Atur Serikat
Gabungan himpunan A dan B (dilambangkan dengan $ A \ cup B $) adalah himpunan elemen yang ada di A, di B, atau di A dan B. Karenanya, $ A \ cup B = \ lbrace x \: | \: x \ di A \ OR \ x \ di B \ rbrace $.
Example- Jika $ A = \ lbrace 10, 11, 12, 13 \ rbrace $ dan B = $ \ lbrace 13, 14, 15 \ rbrace $, maka $ A \ cup B = \ lbrace 10, 11, 12, 13, 14 , 15 \ rbrace $. (Elemen umum hanya terjadi sekali)
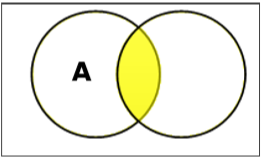
Atur Persimpangan
Perpotongan himpunan A dan B (dilambangkan dengan $ A \ cap B $) adalah himpunan elemen yang berada di A dan B. Karenanya, $ A \ cap B = \ lbrace x \: | \: x \ in A \ DAN \ x \ dalam B \ rbrace $.
Example - Jika $ A = \ lbrace 11, 12, 13 \ rbrace $ dan $ B = \ lbrace 13, 14, 15 \ rbrace $, maka $ A \ cap B = \ lbrace 13 \ rbrace $.
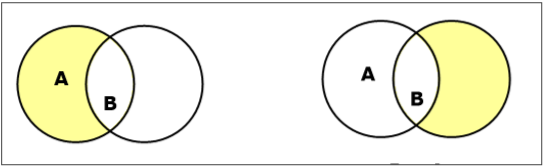
Tetapkan Selisih / Pelengkap Relatif
Perbedaan himpunan dari himpunan A dan B (dilambangkan dengan $ A - B $) adalah himpunan elemen yang hanya ada di A tetapi tidak di B. Karenanya, $ A - B = \ lbrace x \: | \: x \ di A \ AND \ x \ notin B \ rbrace $.
Example- Jika $ A = \ lbrace 10, 11, 12, 13 \ rbrace $ dan $ B = \ lbrace 13, 14, 15 \ rbrace $, maka $ (A - B) = \ lbrace 10, 11, 12 \ rbrace $ dan $ (B - A) = \ lbrace 14, 15 \ rbrace $. Di sini, kita dapat melihat $ (A - B) \ ne (B - A) $
Pelengkap Set
Komplemen dari himpunan A (dilambangkan dengan $ A '$) adalah himpunan elemen yang tidak ada dalam himpunan A. Oleh karena itu, $ A' = \ lbrace x | x \ notin A \ rbrace $.
Lebih khusus lagi, $ A '= (U - A) $ di mana $ U $ adalah himpunan universal yang berisi semua objek.
Example- Jika $ A = \ lbrace x \: | \: x \ \: {milik \: ke \: set \: dari \: odd \: integers} \ rbrace $ lalu $ A '= \ lbrace y \: | \: y \ \: {tidak \: bukan \: milik \: ke \: set \: dari \: odd \: integers} \ rbrace $

Produk Cartesian / Produk Silang
Produk Kartesius dari n jumlah set $ A_1, A_2, \ dots A_n $ dilambangkan sebagai $ A_1 \ times A_2 \ dots \ times A_n $ dapat didefinisikan sebagai semua kemungkinan pasangan terurut $ (x_1, x_2, \ dots x_n) $ di mana $ x_1 \ di A_1, x_2 \ di A_2, \ dots x_n \ di A_n $
Example - Jika kita ambil dua set $ A = \ lbrace a, b \ rbrace $ dan $ B = \ lbrace 1, 2 \ rbrace $,
Produk Cartesian dari A dan B ditulis sebagai - $ A \ times B = \ lbrace (a, 1), (a, 2), (b, 1), (b, 2) \ rbrace $
Produk Cartesian dari B dan A ditulis sebagai - $ B \ times A = \ lbrace (1, a), (1, b), (2, a), (2, b) \ rbrace $
Set Daya
Himpunan daya dari suatu himpunan S adalah himpunan dari semua himpunan bagian dari S termasuk himpunan kosong. Kardinalitas himpunan pangkat dari himpunan S kardinalitas n adalah $ 2 ^ n $. Perangkat daya dilambangkan sebagai $ P (S) $.
Example −
Untuk satu set $ S = \ lbrace a, b, c, d \ rbrace $ mari kita hitung subsetnya -
Himpunan bagian dengan 0 elemen - $ \ lbrace \ emptyset \ rbrace $ (set kosong)
Subset dengan 1 elemen - $ \ lbrace a \ rbrace, \ lbrace b \ rbrace, \ lbrace c \ rbrace, \ lbrace d \ rbrace $
Subset dengan 2 elemen - $ \ lbrace a, b \ rbrace, \ lbrace a, c \ rbrace, \ lbrace a, d \ rbrace, \ lbrace b, c \ rbrace, \ lbrace b, d \ rbrace, \ lbrace c, d \ rbrace $
Himpunan bagian dengan 3 elemen - $ \ lbrace a, b, c \ rbrace, \ lbrace a, b, d \ rbrace, \ lbrace a, c, d \ rbrace, \ lbrace b, c, d \ rbrace $
Himpunan bagian dengan 4 elemen - $ \ lbrace a, b, c, d \ rbrace $
Karenanya, $ P (S) = $
$ \ lbrace \ quad \ lbrace \ emptyset \ rbrace, \ lbrace a \ rbrace, \ lbrace b \ rbrace, \ lbrace c \ rbrace, \ lbrace d \ rbrace, \ lbrace a, b \ rbrace, \ lbrace a, c \ rbrace, \ lbrace a, d \ rbrace, \ lbrace b, c \ rbrace, \ lbrace b, d \ rbrace, \ lbrace c, d \ rbrace, \ lbrace a, b, c \ rbrace, \ lbrace a, b, d \ rbrace, \ lbrace a, c, d \ rbrace, \ lbrace b, c, d \ rbrace, \ lbrace a, b, c, d \ rbrace \ quad \ rbrace $
$ | P (S) | = 2 ^ 4 = 16 $
Note - Perangkat daya dari perangkat kosong juga merupakan perangkat kosong.
$ | P (\ lbrace \ emptyset \ rbrace) | = 2 ^ 0 = 1 $
Mempartisi Set
Partisi himpunan, misalnya S , adalah kumpulan dari n himpunan bagian yang terputus-putus, misalnya $ P_1, P_2, \ titik P_n $ yang memenuhi tiga kondisi berikut -
$ P_i $ tidak berisi set kosong.
$ \ lbrack P_i \ ne \ lbrace \ emptyset \ rbrace \ untuk \ semua \ 0 \ lt saya \ le n \ rbrack $
Gabungan himpunan bagian harus sama dengan seluruh himpunan asli.
$ \ lbrack P_1 \ cangkir P_2 \ cangkir \ titik \ cangkir P_n = S \ rbrack $
Perpotongan dari dua set berbeda mana pun kosong.
$ \ lbrack P_a \ cap P_b = \ lbrace \ emptyset \ rbrace, \ untuk \ a \ ne b \ di mana \ n \ ge a, \: b \ ge 0 \ rbrack $
Example
Misalkan $ S = \ lbrace a, b, c, d, e, f, g, h \ rbrace $
Satu kemungkinan partisi adalah $ \ lbrace a \ rbrace, \ lbrace b, c, d \ rbrace, \ lbrace e, f, g, h \ rbrace $
Partisi lain yang memungkinkan adalah $ \ lbrace a, b \ rbrace, \ lbrace c, d \ rbrace, \ lbrace e, f, g, h \ rbrace $
Nomor Bel
Nomor bel memberikan jumlah cara untuk mempartisi satu set. Mereka dilambangkan dengan $ B_n $ di mana n adalah kardinalitas himpunan.
Example -
Misalkan $ S = \ lbrace 1, 2, 3 \ rbrace $, $ n = | S | = 3 $
Partisi alternatifnya adalah -
1. $ \ emptyset, \ lbrace 1, 2, 3 \ rbrace $
2. $ \ lbrace 1 \ rbrace, \ lbrace 2, 3 \ rbrace $
3. $ \ lbrace 1, 2 \ rbrace, \ lbrace 3 \ rbrace $
4. $ \ lbrace 1, 3 \ rbrace, \ lbrace 2 \ rbrace $
5. $ \ lbrace 1 \ rbrace, \ lbrace 2 \ rbrace, \ lbrace 3 \ rbrace $
Karenanya $ B_3 = 5 $