Pengantar Pohon
Treeadalah struktur diskrit yang merepresentasikan hubungan hierarki antara elemen atau node individual. Pohon yang salah satu induknya memiliki tidak lebih dari dua anak disebut pohon biner.
Pohon dan Properti-nya
Definition- Pohon adalah graf tak berarah asiklik yang terhubung. Ada jalur unik antara setiap pasangan simpul di $ G $. Sebuah pohon dengan jumlah simpul N berisi $ (N-1) $ jumlah sisi. Titik puncak yang besarnya 0 derajat disebut akar pohon. Titik puncak yang 1 derajat disebut simpul daun pohon dan derajat simpul internal paling sedikit 2.
Example - Berikut adalah contoh pohon -
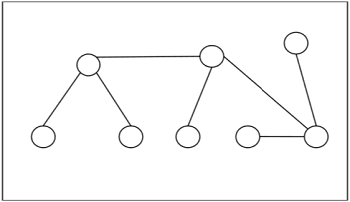
Pusat dan Bi-Pusat Pohon
Pusat pohon adalah puncak dengan eksentrisitas minimal. Eksentrisitas dari simpul $ X $ pada pohon $ G $ adalah jarak maksimum antara simpul $ X $ dan simpul lain dari pohon. Eksentrisitas maksimum adalah diameter pohon. Jika sebuah pohon hanya memiliki satu pusat maka disebut Pohon Sentral dan jika pohon hanya mempunyai lebih dari satu pusat maka disebut Pohon Bi-sentral. Setiap pohon bisa berupa pusat atau dua pusat.
Algoritma untuk mencari center dan bi-center dari sebuah pohon
Step 1 - Hapus semua simpul pada derajat 1 dari pohon yang diberikan dan juga hilangkan tepi datangnya.
Step 2- Ulangi langkah 1 sampai salah satu simpul atau dua simpul yang digabungkan dengan sebuah sisi tersisa. Jika satu simpul tersisa maka itu adalah pusat dari pohon dan jika dua simpul yang digabungkan dengan sebuah sisi dibiarkan maka itu adalah bi-center dari pohon.
Problem 1
Cari tahu center / bi-center dari pohon berikut -
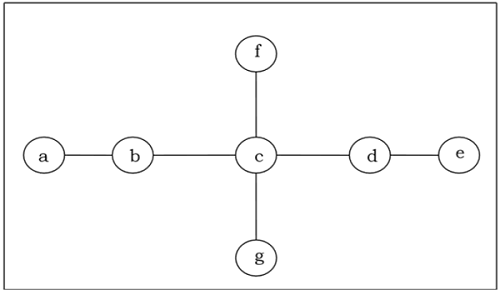
Solution
Pertama-tama, kita akan menghapus semua simpul dengan derajat 1 dan juga menghilangkan tepi datangnya dan mendapatkan pohon berikut -
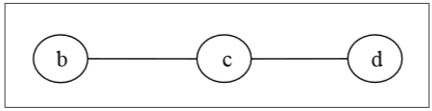
Sekali lagi, kami akan menghapus semua simpul dengan derajat 1 dan juga menghapus tepi insidennya dan mendapatkan pohon berikut -
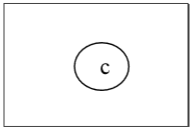
Akhirnya kami mendapat satu titik 'c' dan kami menghentikan algoritme. Karena ada satu simpul, pohon ini memiliki satu pusat 'c' dan pohon itu adalah pohon pusat.
Problem 2
Cari tahu center / bi-center dari pohon berikut -
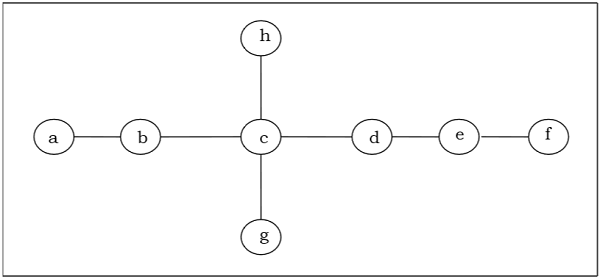
Solution
Pertama-tama, kita akan menghapus semua simpul dengan derajat 1 dan juga menghilangkan tepi datangnya dan mendapatkan pohon berikut -

Sekali lagi, kami akan menghapus semua simpul dengan derajat 1 dan juga menghapus tepi insidennya dan mendapatkan pohon berikut -
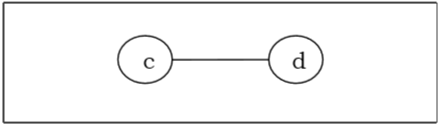
Akhirnya, kami mendapat dua simpul 'c' dan 'd' kiri, maka kami menghentikan algoritma. Karena tersisa dua simpul yang digabungkan dengan sebuah sisi, pohon ini memiliki bi-center 'cd' dan pohon itu bi-central.
Pohon Berlabel
Definition- Pohon berlabel adalah pohon yang simpulnya diberi nomor unik dari 1 sampai n. Kita dapat menghitung pohon seperti itu untuk nilai kecil n dengan tangan untuk menduga rumus umum. Jumlah pohon berlabel n jumlah simpul adalah $ n ^ {n-2} $. Dua pohon berlabel isomorfik jika grafiknya isomorfik dan titik-titik yang bersesuaian dari kedua pohon memiliki label yang sama.
Contoh
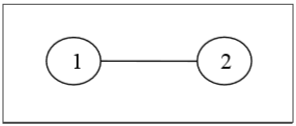
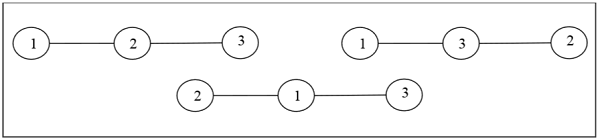
Pohon Tanpa Label
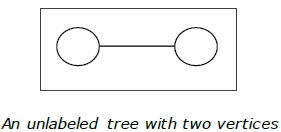
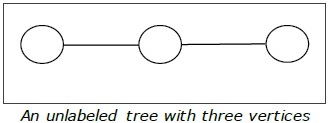
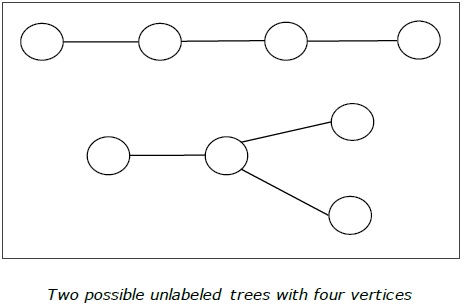
Definition- Pohon yang tidak berlabel adalah pohon yang simpulnya tidak diberi nomor apapun. Jumlah pohon berlabel n jumlah puncak adalah $ \ frac {(2n)!} {(N + 1)! N! } $ (N th nomor Catalan)
Contoh
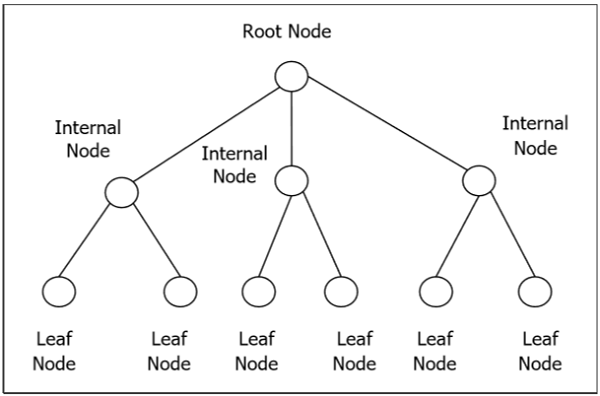
Pohon Berakar
Pohon berakar $ G $ adalah grafik asiklik yang terhubung dengan simpul khusus yang disebut akar pohon dan setiap tepi secara langsung atau tidak langsung berasal dari akar. Pohon berakar teratur adalah pohon berakar di mana anak-anak dari setiap simpul internal diurutkan. Jika setiap simpul dalam dari pohon yang berakar tidak lebih dari m anak, itu disebut pohon m-ary. Jika setiap simpul dalam dari pohon yang berakar mempunyai tepat m anak, itu disebut pohon m-ary penuh. Jika $ m = 2 $, pohon berakar disebut pohon biner.
Pohon Pencarian Biner
Pohon Pencarian Biner adalah pohon biner yang memenuhi properti berikut -
- $ X $ di sub-pohon kiri simpul $ V, Nilai (X) \ le Nilai (V) $
- $ Y $ di sub-pohon kanan dari simpul $ V, Nilai (Y) \ ge Nilai (V) $
Jadi, nilai semua simpul dari sub-pohon kiri dari simpul internal $ V $ kurang dari atau sama dengan $ V $ dan nilai semua simpul dari sub-pohon kanan dari simpul internal $ V $ lebih besar dari atau sama dengan $ V $. Jumlah tautan dari simpul akar ke simpul terdalam adalah ketinggian Pohon Pencarian Biner.
Contoh
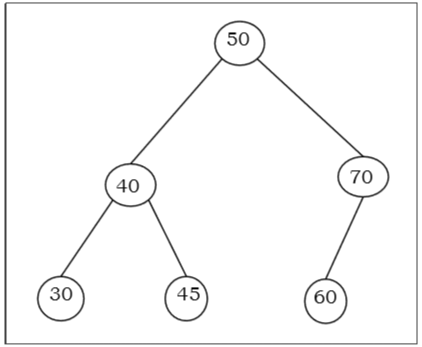
Algoritma untuk mencari kunci di BST
BST_Search(x, k)
if ( x = NIL or k = Value[x] )
return x;
if ( k < Value[x])
return BST_Search (left[x], k);
else
return BST_Search (right[x], k)Kompleksitas pohon pencarian biner
| Kasus Rata-rata | Kasus terburuk | |
|---|---|---|
| Kompleksitas Ruang | Di) | Di) |
| Kompleksitas Pencarian | O (log n) | Di) |
| Kompleksitas Penyisipan | O (log n) | Di) |
| Kompleksitas Penghapusan | O (log n) | Di) |